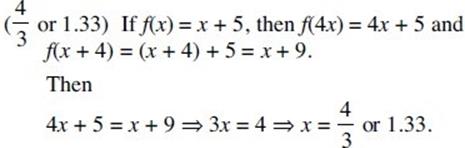Part 3. TACTICS AND PRACTICE: CRITICAL READING

Chapter 9. Reviewing Mathematics

This chapter provides a comprehensive review of all of the mathematics that you need to know for the SAT. Let’s start by saying what you don’t need to know. The SAT is not a test in high school mathematics. There are no questions on trigonometry, logarithms, complex numbers, exponential functions, geometric transformations, parabolas, ellipses, hyperbolas, truth tables, combinations and permutations, or standard deviation. You will not have to graph a straight line, use the quadratic formula, know the equation of a circle, write a geometry proof, do a compass and straightedge construction, prove a trig identity, or solve a complicated word problem. What do you need to know?

About 85 percent of the test questions are divided approximately evenly among topics in arithmetic, elementary algebra, and the fundamentals of geometry. The remaining 15 percent of the questions represent a few basic miscellaneous topics, such as probability and counting, interpretation of data, functions, and logical reasoning. Surprisingly, a lot of the mathematics that you need to know for the SAT you learned before you left middle school or junior high school. There are some questions on elementary algebra, basic geometry, and concepts of functions— material that you have learned in high school—but not very many.

Why, then, if no advanced mathematics is on the SAT, do so many students find some of the questions difficult? The answer is that the College Board considers the SAT to be “a test of general reasoning abilities.” It attempts to use basic concepts of arithmetic, algebra, and geometry as a method of testing your ability to think logically. The Board is not testing whether you know how to calculate an average, find the area of a circle, use the Pythagorean theorem, or read a bar graph. It assumes you can. In fact, because the Board is not even interested in testing your memory, many of the formulas you will need are listed at the beginning of each math section. In other words, the College Board’s objective is to use your familiarity with numbers and geometric figures as a way of testing your logical thinking skills.

Since, to do well on the SAT, you must know basic arithmetic, algebra, and geometry, this chapter reviews everything you need to know. But that’s not enough. You have to be able to use these concepts in ways that may be unfamiliar to you. That’s where the tactics and strategies from Chapter 8 come in.

This chapter is divided into 18 sections, numbered 9-A through 9-R. Each section deals with a different topic, and in it you are given the basic definitions, key facts, and tactics that you need to solve SAT-type questions on that topic. The especially important facts, which are referenced in the solutions to sample problems and to the Model Tests in Part Four, are labeled KEY FACTS and are numbered. Following each KEY FACT are one or more sample SAT-type questions that use that fact. Also included in some sections are test-taking tactics specific to the topics discussed.

Basically, Chapter 9 is broken down as follows:

• Topics in Arithmetic	Sections A–E
• Topics in Algebra	Sections F–H
• Topics in Geometry	Sections I–N
• Miscellaneous Topics	Sections O–R

See the Table of Contents for a list of the specific topics in each section.

No topic, however, really belongs to only one category. Average problems are discussed in the arithmetic sections, but on the SAT you need to be able also to take the average of algebraic expressions and the average of the measures of the angles of a triangle. Most algebra problems involve arithmetic, as well; on many geometry problems you need to use algebra; and several of the problems in the miscellaneous topics sections require a knowledge of arithmetic and/or algebra.

At the end of each section is a set of exercises that consists of a variety of multiple-choice and grid-in questions, similar to actual SAT questions, that utilize the concepts covered in the section. You should use whichever TACTICS and KEY FACTS from that section that you think are appropriate. If you’ve mastered the material in the section, you should be able to answer most of the questions. If you get stuck, you can use the various strategies you learned in Chapter 8; but then you should carefully read the solutions that are provided, so that you understand the correct mathematical way to answer the question. In the solutions some references are made to the TACTICS from Chapter 8, but the major emphasis here is on doing the mathematics properly.

Finally, one small disclaimer is appropriate. This is not a mathematics textbook—it is a review of the essential facts that you need to know to do well on the SAT. Undoubtedly, you have already learned most, if not all, of them. If, however, you find some topics with which you are unfamiliar or on which you need more information, get a copy of Barron’s E-Z Arithmetic, E-Z Algebra, and/or E-Z Geometry. For additional practice on SAT-type questions, see Barron’s Math Workbook for the SAT.

ARITHMETIC

To do well on the SAT, you need to feel comfortable with most topics of basic arithmetic. The first five sections of Chapter 9 provide you with a review of basic arithmetic concepts; fractions and decimals; percents; ratios and proportions; and averages. Because you will have a calculator with you at the test, you will not have to do long division, multiply three-digit numbers, or perform any other tedious calculations by hand. If you use a calculator with fraction capability, you can even avoid finding least common denominators and reducing fractions.

The solutions to more than one-third of the mathematics questions on the SAT depend on your knowing the KEY FACTS in these sections. Be sure to review them all.

9-A Basic Arithmetic Concepts

A set is a collection of “things” that have been grouped together in some way. Those “things” are called the elements or members of the set, and we say that the “thing” is in the set. For example:

• If A is the set of former presidents of the United States, then John Adams is an element of A.

• If B is the set of vowels in the English alphabet, then i is a member of B.

• If C is the set of prime numbers, then 17 is in C.

The symbol for “is an element (or member) of” is ∈, so we can write “17 ∈ C.”

The union of two sets, X and Y, is the set consisting of all the elements that are in X or in Y or in both. Note that this definition includes the elements that are in X and Y. The union is represented as X ∪ Y. Therefore, a ∈ X ∈ ∪ Y if and only if a ∈ X or a ∈ Y.

The intersection of two sets, X and Y, is the set consisting only of the elements that are in both X and Y. The intersection is represented as X ∩ Y. Therefore, b ∈ X ∩ Y if and only if b ∈ X and b ∈ Y.

In describing a set of numbers, we usually list the elements inside a pair of braces. For example, let X be the set of prime numbers less than 10, and let Y be the set of odd positive integers less than 10.

X = {2, 3, 5, 7}                  Y = {1, 3, 5, 7, 9}

X ∪ Y = {1, 2, 3, 5, 7, 9}

X ∩ Y = {3, 5, 7}

The solution set of an equation is the set of all numbers that satisfy the equation.

EXAMPLE 1

If A is the solution set of the equation x² – 4 = 0 and B is the solution set of 
the equation x² – 3x + 2 = 0, how many elements are in the union of the two sets?

Solution. Solving each equation (see Section 9-G if you need to review how to solve a quadratic equation), you get A = {–2, 2} and B = {1, 2}. Therefore, A ∈ ∪ B = {–2, 1, 2}. There are 3 elements in the union.

Let’s start our review of arithmetic by discussing the most important sets of numbers and their properties. On the SAT the word number always means “real number,” a number that can be represented by a point on the number line.

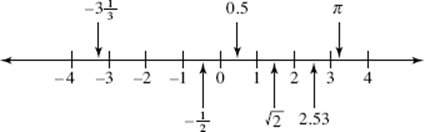
Signed Numbers

The numbers to the right of 0 on the number line are called positive, and those to the left of 0 are negative. Negative numbers must be written with a negative sign (–2); positive numbers can be written with a plus sign (+2) but are usually written without it (2). All numbers can be called signed numbers.

Key Fact A1

For any number a, exactly one of the following is true:

• a is negative.    • a = 0.    • a is positive.

The absolute value of a number a, denoted as |a|, is the distance between a and 0 on the number line. Since 3 is 3 units to the right of 0 on the number line and –3 is 3 units to the left of 0, both have absolute values of 3:

• |3| = 3                  • |–3| = 3

EXAMPLE 2

What is the value of  ?

(A) –8 
(B) –2 
(C)   0 
(D)   2 
(E)   8

Solution.  = 2 (D).

Key Fact A2

For any number a and positive number b:

• |a| = b  a = b or a = –b.

• |a| < b  –b < a < b.

• |a| > b  a < –b or a > b.

EXAMPLE 3

How many integers satisfy the inequality |x| < π? 

(A) 0 
(B) 3 
(C) 4 
(D) 7 
(E) More than 7

Solution. By KEY FACT A2,

|x| < π  –π < x < π  –3.14 < x < 3.14.

There are 7 integers that satisfy this inequality: –3, –2, –1, 0, 1, 2, 3. Choice D is correct.

Arithmetic is basically concerned with the addition, subtraction, multiplication, and division of numbers. Column 3 of the table below shows the terms used to describe the results of these operations.

*Multiplication can be indicated also by a dot, parentheses, or the juxtaposition of symbols without any sign: 2² . 2⁴, 3(4), 3(x + 2), 3a, 4abc.

Given any two numbers a and b, you can always find their sum, difference, product, and quotient (with a calculator, if necessary), except that we can never divide by zero:

• 0 ÷ 7 = 0         • 7 ÷ 0 is meaningless.

EXAMPLE 4

What is the sum of the product and the quotient of 7 and 7?

Solution. Product: 7 × 7 = 49. Quotient: 7 ÷ 7 = 1. Sum: 49 + 1 = 50.

Key Fact A3

For any number a: a × 0 = 0. Conversely, if the product of two or more numbers is 0, at least one of them must be 0.

• If ab = 0, then a = 0 or b = 0.

• If xyz = 0, then x = 0 or y = 0 or z = 0.

EXAMPLE 5

What is the product of all the integers from –3 to 6?

Solution. Before reaching for your calculator, think. You are asked for the product of 10 numbers, one of which is 0. Then, by KEY FACT A3, the product is 0.

Key Fact A4

The product and the quotient of two positive numbers or two negative numbers are positive; the product and the quotient of a positive number and a negative number are negative.

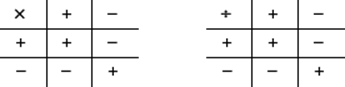
6 × 3 = 18   6 × (–3) = –18   (–6) × 3 = –18   (–6) × (–3) = 18
6 ÷ 3 = 2     6 ÷ (–3) = –2     (–6) ÷ 3 = –2     (–6) ÷ (–3) = 2

To determine whether a product of more than two numbers is positive or negative, count the number of negative factors.

Key Fact A5

• The product of an even number of negative factors is positive.

• The product of an odd number of negative factors is negative.

EXAMPLE 6

If the product of 10 numbers is positive, what is the greatest number of them that could be negative? 

(A)   0 
(B)   1 
(C)   5 
(D)   9 
(E) 10

Solution. Since by KEY FACT A5, the product of 10 negative numbers is positive, all 10 of the numbers could be negative (E).

Key Fact A6

The reciprocal of any nonzero number a is .

The product of any number and its reciprocal is 1: a = 1.

Key Fact A7

• The sum of two positive numbers is positive.

• The sum of two negative numbers is negative.

• To find the sum of a positive and a negative number, find the difference of their absolute values and use the sign of the number with the larger absolute value.

        6 + 2 = 8          (–6) + (–2) = –8

To calculate either 6 + (–2) or (–6) + 2, take the difference, 6 – 2 = 4, and use the sign of the number whose absolute value is 6:

6 + (–2) = 4          (–6) + 2 = –4

Key Fact A8

The sum of any number and its opposite is 0: a + (–a) = 0.

Many properties of arithmetic depend on the relationships between subtraction and addition and between division and multiplication. Subtracting a number is the same as adding its opposite, and dividing by a number is the same as multiplying by its reciprocal.

a –b =a + (–b)    a ÷ b =a 

Many problems involving subtraction and division can be simplified by changing them to addition and multiplication problems, respectively.

Key Fact A9

To subtract signed numbers, change the problem to an addition problem by changing the sign of what is being subtracted, and then use KEY FACT A7.

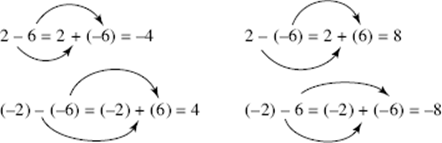
In each case, the minus sign was changed to a plus sign, and either the 6 was changed to –6 or the –6 was changed to 6.

 CALCULATOR HINT

All arithmetic involving signed numbers can be accomplished on any calculator, but not all calculators handle negative numbers in the same way. Be sure you know how to enter negative numbers and how to use them on your calculator.

Integers

The integers are {..., –4, –3, –2, –1, 0, 1, 2, 3, 4, ...}.

The positive integers are {1, 2, 3, 4, 5, ...}.

The negative integers are {..., –5, –4, –3, –2, –1}.

Note: The integer 0 is neither positive nor negative. Therefore, if an SAT question asks how many positive numbers have a certain property, and the only numbers with that property are –2, –1, 0, 1, and 2, the answer is 2.

Consecutive integers are two or more integers, written in sequence, each of which is 1 more than the preceding integer. For example:

22, 23   6, 7, 8, 9   –2, –1, 0, 1   n, n + 1, n + 2, n + 3

EXAMPLE 7

If the sum of three consecutive integers is less than 75, what is the greatest possible value of the smallest of the three integers?

Solution. Let the numbers be n, n + 1, and n + 2. Then

n + (n + 1) + (n + 2) = 3n + 3  3n + 3 < 75  3n < 72  n < 24.

The most n can be is 23. (See Section 9-G for help in solving inequalities like this one.)

Of course, you don’t need to do the algebra (see Chapter 8, TACTIC 7). Try three consecutive integers near 25, say 24, 25, 26. Their sum is 75, which is slightly too big (the sum needs to be less than 75), so the numbers must be 23, 24, 25.

CAUTION: Never assume that number means integer: 3 is the only integer between 2 and 4, but there are infinitely many numbers between 2 and 4, including 2.5, 3.99, , π, and .

EXAMPLE 8

If 2 < x < 4 and 3 < y < 7, what is the largest integer value of x + y?

Solution. If x and y are integers, the largest value is 3 + 6 = 9. However, although x +y is to be an integer, neither x nor y must be. If x = 3.8 and y = 6.2, then x + y = 10.

The sum, the difference, and the product of two integers are always integers; the quotient of two integers may be, but is not necessarily, an integer. The quotient 23 ÷ 10 can be expressed as  or 2.3. If the quotient is to be an integer, we can also say that the quotient is 2 and there is a remainder of 3.

The way we express the answer depends on the question.For example, if $23 are to be divided among 10 people, each one will get $2.30 (2.3 dollars); but if 23 books are to be divided among 10 people, each one will get 2 books and 3 will be left over (the remainder).

Calculator Shortcut

The standard way to find quotients and remainders is to use long division; but on the SAT, you never do long division: you use your calculator. To find the remainder when 100 is divided by 7, divide on your calculator: 100 ÷ 7 = 14.285714.... This tells you that the quotient is 14. (Ignore everything to the right of the decimal point.) To find the remainder, multiply: 14 × 7 = 98, and then subtract:100 – 98 = 2.

EXAMPLE 9

If a is the remainder when 999 is divided by 7, and b is the remainder when 777 is divided by 9, what is the remainder when a is divided by b?

Solution.

999 ÷ 7 = 142.714…; 7 × 142 = 994; 999 – 994 = 5 = a.

777 ÷ 9 = 86.333…; 9 × 86 = 774; 777 – 774 = 3 = b.

Finally, when 5 is divided by 3, the quotient is 1 and the remainder is 2.

EXAMPLE 10

How many positive integers less than 100 have a remainder of 3 when divided by 7?

Solution. To have a remainder of 3 when divided by 7, an integer must be 3 more than a multiple of 7. For example, when 73 is divided by 7, the quotient is 10 and the remainder is 3:73 = 10 × 7 + 3. Just take the multiples of 7 and add 3:

0 × 7 + 3 = 3;      1 × 7 + 3 = 10;      2 × 7 + 3 = 17; ...; 13 × 7 + 3 = 94

There are 14 positive integers less than 100 that have a remainder of 3 when divided by 7.

If a and b are integers, the following four terms are synonymous:

 a is a divisor of b.         a. is a factor of b.

b is a divisible by a.      b is a multiple of a.

All these statements mean that, when b is divided by a, there is no remainder (or, more precisely, the remainder is 0). For example:

3 is a divisor of 12.     3 is a factor of 12.

12 is divisible by 3.    12 is a multiple of 3.

Key Fact A10

Every integer has a finite set of factors (or divisors) and an infinite set of multiples.

The factors of 12:       –12, –6, –4, –3, –2, –1, 1, 2, 3, 4, 6, 12

The multiples of 12:  ..., –48, –36, –24, –12, 0, 12, 24, 36, 48, ...

The only positive divisor of 1 is 1. Every other positive integer has at least two positive divisors:1 and itself, and possibly many more. For example, 6 is divisible by 1 and 6, as well as by 2 and 3; whereas 7 is divisible only by 1 and 7. Positive integers, such as 7, that have exactly two positive divisors are called prime numbers or primes. Here are the first several primes:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29

Memorize this list—it will come in handy. Note that 1 is not a prime.

Helpful Hint

Memorize the list of the ten smallest primes.

Key Fact A11

Every integer greater than 1 that is not a prime can be written as a product of primes.

CAUTION

1 is not a prime.

To find the prime factorization of any integer, find any two factors: if they’re both primes, you are done; if not, factor them. Continue until each factor has been written in terms of primes.

A useful method is to make a factor tree.

For example, here are the prime factorizations of 108 and 240:

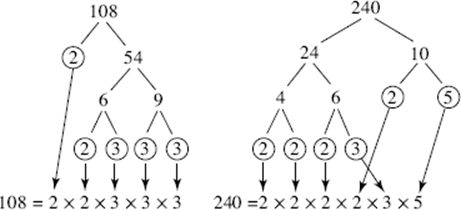
EXAMPLE 11

For any positive integer a, let a denote the smallest prime factor of a. Which of the following is equal to 35? 

(A) 10 
(B) 15 
(C) 45 
(D) 55 
(E)  75

Solution. Check the first few primes; 35 is not divisible by 2 or 3, but is divisible by 5, so 5 is the smallest prime factor of 35, and 35 = 5. Now check the five choices: 10 = 2, and 15, 45, and 75 are all equal to 3. Only 55 = 5. The answer is D.

The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of each of them. For example, the LCM of 6 and 10 is 30. Infinitely many positive integers are multiples of both 6 and 10, including 60, 90, 180, 600, 6000, and 66,000,000, but 30 is the smallest one.

The greatest common factor (GCF) or greatest common divisor (GCD) of two or more integers is the largest integer that is a factor of each of them. For example, the only positive integers that are factors of both 6 and 10 are 1 and 2, so the GCF of 6 and 10 is 2. For small numbers, you can often find the GCF and LCM by inspection. For larger numbers, KEY FACTS A12 and A13 are useful.

Key Fact A12

The product of the GCF and LCM of two numbers is equal to the product of the two numbers.

Helpful Hint

It is usually easier to find the GCF than the LCM. For example, you may see immediately that the GCF of 36 and 48 is 12. You can then use KEY FACT A12 to find the LCM: since GCF × LCM = 36 × 48:

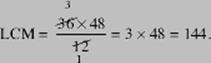
Key Fact A13

To find the GCF or LCM of two or more integers, first get their prime factorizations.

• The GCF is the product of all the primes that appear in each of the factorizations, using each prime the smallest number of times it appears in any factorization.

• The LCM is the product of all the primes that appear in any of the factorizations, using each prime the largest number of times it appears in any factorization.

For example, let’s find the GCF and LCM of 108 and 240. As we saw:

108 = 2 × 2 × 3 × 3 × 3 and 240 = 2 × 2 × 2 × 2 × 3 × 5.

• GCF. The primes that appear in both factorizations are 2 and 3. Since 2 appears twice in the factorization of 108 and 4 times in the factorization of 240, we take it twice; 3 appears 3 times in the factorization of 108, but only once in the factorization of 240, so we take it just once. The GCF = 2 × 2 × 3 = 12.

• LCM. We take one of the factorizations and add to it any primes from the other that are not yet listed. We’ll start with 2 × 2 × 3 × 3 × 3 (108) and look at the primes from 240. There are four 2’s; we already wrote two 2’s, so we need two more; there is a 3, but we already have that; there is a 5, which we need. The LCM = (2 × 2 × 3 × 3 × 3) × (2 × 2 × 5) = 108 × 20 = 2160.

EXAMPLE 12

What is the smallest number that is divisible by both 34 and 35?

Solution. You are being asked for the LCM of 34 and 35.

By KEY FACT A12, the LCM =  The GCF, however, is 1 since no number greater than 1 divides evenly into both 34 and 35. The LCM is 34 × 35 = 1190.

The even numbers are all the multiples of 2: {..., –4, –2, 0, 2, 4, 6, ...}.

The odd numbers are all the integers not divisible by 2: {..., –5, –3, –1, 1, 3, 5, ...}.

Note: • The terms odd and even apply only to integers.
• Every integer (positive, negative, or 0) is either odd or even.
• 0 is an even integer; it is a multiple of 2 (0 = 0 × 2).
• 0 is a multiple of every integer (0 = 0 × n).
• 2 is the only even prime number.

NOTE

• The GCF of two consecutive integers is 1.

• The GCF of two consecutive even integers is 2.

Key Fact A14

The tables below summarize three important facts:

1. If two integers are both even or both odd, their sum and difference are even.

2. If one integer is even and the other odd, their sum and difference are odd.

3. The product of two integers is even unless both of them are odd.

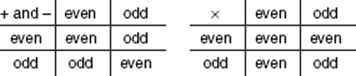
Exponents and Roots

Repeated addition of the same number is indicated by multiplication:

17 + 17 + 17 + 17 + 17 + 17 + 17 = 7 × 17.

Repeated multiplication of the same number is indicated by an exponent:

17 × 17 × 17 × 17 × 17 × 17 × 17 = 17⁷.

In the expression 17⁷, 17 is called the base and 7 is the exponent.

On the SAT, most of the exponents you will encounter are positive integers; these are defined in KEY FACT A15. Occasionally you may see an exponent that is zero or negative or is a fraction; these exponents are defined later in KEY FACT A20.

Key Fact A15

For any number b: b¹ = b.

For any number b and integer n > 1: bⁿ = b × b ×  × b, where b is used as a factor n times.

(i) 2⁵ × 2³ = (2 × 2 × 2 × 2 × 2) × (2 × 2 × 2) = 2⁸ = 2⁵⁺³.

(ii) = 2 × 2 = 2² = 2^5–3.

(iii) (2²)³ = (2 × 2)³ = (2 × 2) × (2 × 2) × (2 × 2) = 2⁶ = 2^{2 × 3}.

(iv) 2³ × 7³ = (2 × 2 × 2) × (7 × 7 × 7) = (2 × 7)(2 × 7) (2 × 7) = (2 × 7)³.

(v) .

These five examples illustrate the five important laws of exponents given in KEY FACT A16.

Helpful Hint

Memorize these laws of exponents; they are very useful.

Key Fact A16

For any numbers b and c and positive integers m and n:

(i) b^mbⁿ = b^m+n    (ii)    (iii) (b^m)ⁿ = b^mn   (iv) b^mc^m = (bc)^m   (v) 

CAUTION: In (i) and (ii) the bases are the same, and in (iv) the exponents are the same. None of these rules applies to expressions such as 2⁵ × 3⁴, in which both the bases and the exponents are different.

EXAMPLE 13

If 2^x = 32, what is x²?

Solution. To solve 2^x = 32, just count (and keep track of) how many 2’s you need to multiply to get 32: 2 × 2 × 2 × 2 × 2 = 32, so x = 5 and x² = 25.

Helpful Hint

Write out the first ten powers of 2 and memorize them.

EXAMPLE 14

If 3^a × 3^b = 3¹⁰⁰, what is the average (arithmetic mean) of a and b?

Solution. Since 3^a × 3^b = 3^a+b, you can see that
a + b = 100  = 50.

The next KEY FACT is an immediate consequence of KEY FACTS A4 and A5.

Key Fact A17

For any positive integer n:

  (i) 0ⁿ = 0.

 (ii) If a is positive, aⁿ is positive.

(iii) If a is negative, aⁿ is positive if n is even, and negative if n is odd.

EXAMPLE 15

Which of the following statements is (are) true?

  I. –2¹⁰ > 0 

 II. – (–2)¹⁰ > 0 

III. 210 – (–2)¹⁰ > 0 

(A) None 
(B) I only 
(C) III only 
(D) I and III only 
(E) I, II, and III

Solution.

Since 2¹⁰ is positive, –2¹⁰ is negative. (I is false.)

Since (–2)¹⁰ is positive, – (–2)¹⁰ is negative. (II is false.)

Since (–2)¹⁰ = 2¹⁰, 2¹⁰ – (–2)¹⁰ = 0. (III is false.)

None of the statements is true. Choice A is correct.

Squares and Square Roots

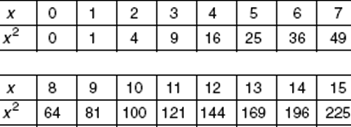
The exponent that appears most often on the SAT is 2. It is used to form the square of a number, as in πr² (the area of a circle), a² + b² = c² (the Pythagorean theorem), or x² – y² (the difference of two squares). Therefore, it is helpful to recognize the perfect squares, numbers that are the squares of integers. The squares of the integers from 0 to 15 are as follows:

There are two numbers that satisfy the equation x ² = 9: x = 3 and x = –3. The positive number, 3, is called the square root of 9 and is denoted by the symbol .

Clearly, each perfect square has a square root:  It is an important fact, however, that every positive number has a square root.

Key Fact A18

For any positive number a, there is a positive number b that satisfies the equation b² = a. That number is called the square root of a, and we write b = .

Therefore, for any positive number a:  ×  = ()² = a.

The only difference between  and  is that the first square root is an integer, while the second one isn’t. Since 10 is a little more than 9, we should expect that  is a little more than , which is 3. In fact, (3.1)² = 9.61, which is close to 10; and (3.16)² = 9.9856, which is very close to 10, so  ≈ 3.16. Square roots of integers that aren’t perfect squares can be approximated as accurately as we wish, and by pressing the  key on our calculators we can get much more accuracy than is needed for the SAT. Actually, most answers involving square roots use the square root symbol.

EXAMPLE 16

What is the circumference of a circle whose area is 10π? 
(A) 5π 
(B) 10π 
(C) π 
(D) 2π 
(E) π

Solution. See Section 9-L for the formulas for the area and circumference of a circle. Since the area of a circle is given by the formula A = πr², then

πr² = 10π  r² = 10  r = .

Since the circumference is given by the formula C = 2πr, then C = 2π  (D).

Key Fact A19

For any positive numbers a and b:

        and         

CAUTION: 

For example: 5 = 

CAUTION: Although it is always true that ()² = a,  = a is not true if a is negative:

In the same way that we write b =  to indicate that a²= b, we write

b =  to indicate that b³ = a,

and

b =  to indicate that b⁴ = a.

For example,

 = 4 because 4³ = 64,

and

 = 2 because 2⁴ = 16.

So far, the only exponents we have considered have been positive integers. We now expand our definition to include other numbers as exponents.

Key Fact A20

• For any real number a ≠ 0: a⁰ = 1.

• For any real number a ≠ 0: a^–n = .

• For any positive number a and positive integer n: .

Here are some examples to illustrate the definitions in KEY FACT A20:

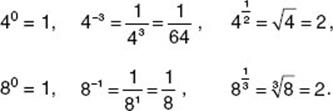
Key Fact A21

The laws of exponents given in KEY FACT A16 are true for any exponents, not just positive integers.

For example:

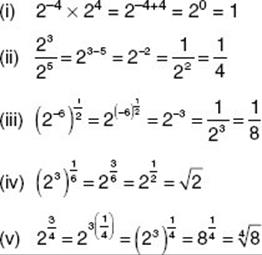
REMEMBER

All exponents satisfy the basic laws of exponents.

EXAMPLE 17

What is the value of   

Solution. 

PEMDAS

When a calculation requires performing more than one operation, it is important to carry the operations out in the correct order. For decades students have memorized the sentence “Please Excuse My Dear Aunt Sally,” or just the acronym, PEMDAS, to remember the proper order of operations. The letters stand for:

• Parentheses: first do whatever appears in parentheses, following PEMDAS within the parentheses also if necessary.

• Exponents: next evaluate all terms with exponents.

• Multiplication and Division: then do all multiplications and divisions in order from left to right—do not multiply first and then divide.

• Addition and Subtraction: finally, do all additions and subtractions in order from left to right—do not add first and then subtract.

Calculator Shortcut

Almost every scientific and graphing calculator automatically follows PEMDAS. Test each of these calculations on your calculator. Be sure you know whether or not you need to use parentheses or to put anything in memory as you proceed.

Here are some worked-out examples.

1. 12 + 3 × 2 = 12 + 6 = 18     [Multiply before you add.] 
(12 + 3) × 2 = 15 × 2 = 30  [First add in the parentheses.]

2. 12 ÷ 3 × 2 = 4 × 2 = 8         [Just go from left to right.] 
12 ÷ (3 × 2) = 12 ÷ 6 = 2    [Multiply first.]

3. 5 × 2³ = 5 × 8 = 40              [Do the exponent first.] 
(5 × 2)³ = 10³ = 1000           [Multiply first.]

4. 4 + 4 ÷ (2 + 6) = 4 + 4 ÷ 8 = 4 + .5 = 4.5 
[Do parentheses first, then division.]

5. 100 – 2²(3 + 4 × 5) = 100 – 2²(23) = 100 – 4(23) = 100 – 92 = 8 
[Do parentheses first (using PEMDAS), then the exponent, then multiplication.]

There is one situation when you shouldn’t start with what’s in the parentheses. Consider the following two examples.

(i) What is the value of 7(100 – 1)? 
Using PEMDAS, you would write 7(100 – 1) = 7(99); and then, multiplying on your calculator, you would get 693. But you can do the arithmetic more quickly in your head if you think of it this way: 7(100 – 1) = 700 – 7 = 693.

(ii) What is the value of (77 + 49) ÷ 7? 
If you followed the rules of PEMDAS, you would first add: 77 + 49 = 126, and then divide: 126 ÷ 7 = 18. This is definitely more difficult and time-consuming than mentally calculating
 = 11 + 7 = 18.

Both of these examples illustrate the very important distributive law.

Key Fact A22 The Distributive Law

For any real numbers a, b, and c:

• a(b + c) = ab + ac,        • a(b – c) = ab – ac;

and, if a ≠ 0,

•          • 

Helpful Hint

Many students use the distributive law with multiplication but forget about it with division. Don’t make that mistake.

EXAMPLE 18

If a = 3(x – 7) and b = 3x – 7, what is the value of a – b? 

(A) –28 
(B) –14 
(C)     0 
(D) 3x – 14 
(E) 3x + 7

Solution.    a –b = 3(x – 7) – (3x – 7) = 3x – 21 – 3x + 7 = –21 + 7 = –14 (B).

EXAMPLE 19

What is the average (arithmetic mean) of 3¹⁰, 3²⁰, and 3³⁰? 

(A) 60 
(B) 3²⁰ 
(C) 3³⁰ 
(D) 3⁶⁰ 
(E) 3⁹ + 3¹⁹ + 3²⁹

Solution. 

NOTE

The proper use of the distributive law is essential in the algebra review in Section 9-F.

Inequalities

The number a is greater than the number b, denoted as a > b, if a is to the right of b on the number line. Similarly, a is less than b, denoted as a < b, if a is to the left of b on the number line. Therefore, if a is positive, a > 0; and if ais negative, a < 0. Clearly, if a > b, then b < a.

KEY FACT A23 gives an important alternative way to describe greater than and less than.

Key Fact A23

• For any numbers a and b: a > b means that a – b is positive.

• For any numbers a and b: a < b means that a – b is negative.

Key Fact A24

For any numbers a and b, exactly one of the following is true:

a > b or a = b or a < b.

The symbol ≥ means greater than or equal to and the symbol ≤ means less than or equal to. The statement “x ≥ 5” means that x can be 5 or any number greater than 5; the statement “x ≤ 5” means that x can be 5 or any number less than 5.

The statement “2 < x < 5” is an abbreviation for the statement “2 < x and x < 5.” It means that x is a number between 2 and 5 (greater than 2 and less than 5).

KEY FACTS A25 and A26 give some important information about inequalities that you need to know for the SAT.

Key Fact A25 The Arithmetic of Inequalities

• Adding a number to an inequality or subtracting a number from the inequality preserves the inequality. 

If a < b, then a + c < b + c and a – c < b – c.

3 < 7  3 + 100 < 7 + 100 (103 < 107)

3 < 7  3 – 100 < 7 – 100 (–97 < –93)

• Adding inequalities in the same direction preserves them. 

If a < b and c < d, then a + c < b + d.

3 < 7 and 5 < 10  3 + 5 < 7 + 10 (8 < 17)

• Multiplying or dividing an inequality by a positive number preserves the inequality. 
If a < b, and c is positive, then ac < bc and 

3 < 7  3 × 100 < 7 × 100 (300 < 700)

3 < 7  3 ÷ 100 < 7 ÷ 100 

• Multiplying or dividing an inequality by a negative number reverses the inequality. 
If a < b, and c is negative, then ac > bc and .

3 < 7  3 × (–100) > 7 × (–100) (–300 > –700)

3 < 7  3 ÷ (–100) > 7 ÷ (–100) 

• Taking negatives reverses an inequality. 

If a < b, then –a > –b, and if a > b, then –a < –b.

3 < 7  –3 > –7, and 7 > 3  –7 < –3.

• If two numbers are each positive or each negative, taking reciprocals reverses an inequality. 
If a and b are both positive or both negative and a < b, then 

3 < 7   and –7 < –3  

Helpful Hint

Be sure you understand KEY FACT A25; it is very useful. Also, review the important properties listed in KEY FACTS A26–A28. These properties come up frequently on the SAT.

Key Fact A26 Important      Inequalities for Numbers Between 0 and 1

• If 0 < x < 1, and a is positive, then xa < a. 
For example, 0.85 × 19 < 19.

• If 0 < x < 1, and m and n are integers with m > n > 1, then x^m < xⁿ < x. 
For example, .

• If 0 < x < 1, then  > x. 
For example, 

• If 0 < x < 1, then  > x. In fact,  > 1. 
For example,  > 1 > 0.2.

Key Fact A27      Properties of Zero

• 0 is the only number that is neither positive nor negative.

• 0 is smaller than every positive number and greater than every negative number.

• 0 is an even integer.

• 0 is a multiple of every integer.

• For every number a: a + 0 = a and a – 0 = a.

• For every number a: a × 0 = 0.

• For every integer n: 0ⁿ = 0.

• For every number a (including 0): a ÷ 0 and  are meaningless expressions.
(They are undefined.)

• For every number a other than 0: 0 ÷ a =  = 0.

• 0 is the only number that is equal to its opposite: 0 = – 0.

• If the product of two or more numbers is 0, at least one of the numbers is 0.

Key Fact A28      Properties of 1

• For any number a: 1 × a = a and  = a.

• For any integer n: 1ⁿ = 1.

• 1 is a divisor of every integer.

• 1 is the smallest positive integer.

• 1 is an odd integer.

• 1 is the only integer with only one divisor. It is not a prime.

Exercises on Basic Arithmetic Concepts

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

1. For how many positive integers, a, is it true that a² ≤ 2a?

(A) None

(B) 1

(C) 2

(D) 4

(E) More than 4

2. If 0 < a < b < 1, which of the following is (are) true?

  I. a – b is negative.

 II.  is positive.

III.  is positive.

(A) I only

(B) II only

(C) III only

(D) I and II only

(E) I, II, and III

3. If a and b are negative, and c is positive, which of the following is (are) true?

I. a – b < a – c

II. if a < b, then 

III. 

(A) I only

(B) II only

(C) III only

(D) II and III only

(E) I, II, and III

4. At 3:00 A.M. the temperature was 13° below zero. By noon it had risen to 32°. What was the average hourly increase in temperature?

(A) 

(B) 

(C) 5°

(D) 7.5°

(E) 45°

5. If (7^a)(7^b) = , what is d in terms of a, b, and c?

(A) 

(B) c – a – b

(C) a + b – c

(D) c – ab

(E) 

6. If p and q are primes greater than 2, which of the following must be true?

  I. p + q is even.

 II. pq is odd.

III. p² – q² is even.

(A) I only

(B) II only

(C) I and II only

(D) I and III only

(E) I, II, and III

Questions 7 and 8 refer to the following definition.

For any positive integer n, (n) represents the number of positive divisors of n.

7. Which of the following is (are) true?

  I. τ(5) = τ(7)

 II. τ(5) · τ(7) = τ(35)

III. τ(5) + τ(7) = τ(12)

(A) I only

(B) II only

(C) I and II only

(D) I and III only

(E) I, II, and III

8. What is the value of τ(τ(τ(12)))?

(A) 1

(B) 2

(C) 3

(D) 4

(E) 6

9. Which of the following is equal to (7⁸ × 7⁹)¹⁰?

(A) 7²⁷

(B) 7⁸²

(C) 7¹⁷⁰

(D) 49¹⁷⁰

(E) 49⁷²⁰

10. If x  y represents the number of integers greater than x and less than y, what is the value of –π   ?

(A) 2

(B) 3

(C) 4

(D) 5

(E) 6

11. If 0 < x < 1, which of the following lists the numbers in increasing order?

(A) , x, x²

(B) x², x, 

(C) x², , x

(D) x, x², 

(E) x, , x²

Grid-in Questions

12. At Ben’s Butcher Shop 99 pounds of chopped meat is being divided into packages each weighing 2.5 pounds. How many pounds of meat are left when there isn’t enough to make another whole package?

13. Maria has two electronic beepers. One of them beeps every 4 seconds; the other beeps every 9 seconds. If they are turned on at exactly the same time, how many times during the next hour will both beepers beep at the same time?

14. If –7 ≤ x ≤ 7 and 0 ≤ y ≤ 12, what is the greatest possible value of y – x?

15. If x is an integer less than 1000 that has a remainder of 1 when it is divided by 2, 3, 4, 5, 6, or 7, what is one possible value of x?

16. What is the value of 2⁴ ÷ 2^–4?

17. What is the value of 
 (–2 – 3) – (2 – 3) ?

18. For any integer, a, greater than 1, let ↑a↓ be the greatest prime factor of a. What is ↑132↓?

19. If the product of four consecutive integers is equal to one of the integers, what is the largest possible value of one of the integers?

20. If x and y are positive integers, and (13^x) ^y = 13¹³, what is the average (arithmetic mean) of x and y?

Answer Key

1. C   2. D   3. D   4. C

5. B   6. E   7. C   8. C

9. C 10. D 11. B

Answer Explanations

1. (C). Since a is positive, divide both sides of the given inequality by a: a² ≤ 2a  a ≤ 2  a = 1 or 2. There are two positive integers that satisfy the given inequality.

2. (D). • Since a < b, a – b is negative. (I is true.)

• Since a and b are positive, so is their product, ab; and the reciprocal of a positive number is positive. (II is true.)

•  Since the numerator, a – b, ab is negative and the denominator, ab, is positive, the value of the fraction is negative. (III is false.)

3. (D). • Since b is negative and c is positive, 
      b < c  –b > –c  a – b > a – c. 
   (I is false.)

• Since c is positive, dividing by c preserves the inequality. (II is true.)

• Since b is negative,  is negative, and so is 
less than , which is positive. (III is true.)

4. (C). In the 9 hours from 3:00 A.M. to noon, the temperature rose 32 – (–13) = 32 + 13 = 45°. 
Therefore, the average hourly increase was 45 ÷ 9 = 5°.

5. (B). (7^a)(7^b) = 7^a + b, and  = 7^c–d. Therefore: a + b = c – d  a + b + d = c  d = c – a – b.

6. (E). All primes greater than 2 are odd, so p and q are odd, and p + q is even. (I is true.) The product of two odd numbers is odd. (II is true.) Since p and q are odd, so are their squares, and so the difference of the squares is even. (III is true.)

7. (C). Since 5 and 7 have two positive factors each, τ(5) = τ(7). (I is true.) Since 35 has four divisors (1, 5, 7, and 35) and τ(5) · τ(7) = 2 × 2 = 4, II is true. The value of τ(12) is 6, which is not equal to 2 + 2. (III is false.)

8. (C).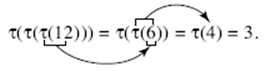

9. (C). First, multiply inside the parentheses: 
7⁸ × 7⁹ = 7¹⁷; then raise to the 10th power: 
(7¹⁷)¹⁰ = 7¹⁷⁰.

10. (D). There are five integers (1, 0, –1, –2, –3) that are greater than –3.14 (–π) and less than 1.41( ).

11. (B). For any number, x, between 0 and 1: x² < x and x < .

12. (1.5)   Divide: 99 ÷ 2.5 = 39.6. The butchers can make 39 packages, weighing a total of 39 × 2.5 = 97.5 pounds, and have 99 – 97.5 = 1.5 pounds of meat left over.

13. (100)   Since 36 is the LCM of 4 and 9, the beepers will beep together every 36 seconds. One hour = 60 minutes = 3600 seconds, and so the simultaneous beeping will occur 100 times.

14. (19)   To make y – x as large as possible, let y be as large as possible (12), and subtract the smallest amount possible (x = –7): 12 – (–7) = 19.

15. (421 or 841)  The LCM of 2, 3, 4, 5, 6, 7 is 420, so 420 is divisible by each of these integers, and there will be a remainder of 1 when 421 is divided by any of them. One more than any multiple of 420 will also work.

16. (256)   2⁴÷2^–4=  =2^4–(–4)=2^{4 + 4}=2⁸=256.

17. (4)        

18. (11) The easiest way to find the greatest prime factor of 132 is to find its prime factorization: 132 = 2 × 2 × 3 × 11, so 11 is the greatest prime factor.

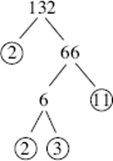
19. (3) If all four integers were negative, their product would be positive, and so could not equal one of them. If all four integers were positive, their product would be much greater than any of them (even 1 × 2 × 3 × 4 = 24). Therefore, the integers must include 0, in which case their product is 0. The largest set of four consecutive integers that includes 0 is 0, 1, 2, 3.

20. (7) Since 13¹³ = (13^x)^y = 13^xy, then xy = 13. The only positive integers whose product is 13 are 1 and 13. Their average is  = 7.

9-B Fractions and Decimals

Several questions on the SAT involve fractions and/or decimals. In this section we will review all of the important facts on these topics that you need to know for the SAT. Even if you are using a calculator with fraction capabilities, it is essential that you review all of this material thoroughly.

When a whole is divided into n equal parts, each part is called one-nth of the whole, written as  . For example, if a pizza is cut (divided) into eight equal slices, each slice is one-eighth  of the pizza; a day is divided into 24 equal hours, so an hour is one-twenty-fourth of a day; and an inch is one-twelfth  of a foot.

• If Sam slept for 5 hours, he slept for five-twenty-fourths  of a day.

• If Tom bought eight slices of pizza, he bought eight-eighths  of a pie.

• If Joe’s shelf is 30 inches long, it measures thirty-twelfths  of a foot.

Numbers such as , , and  in which one integer is written over a second integer, are called fractions. The center line is the fraction bar. The number above the bar is called the numerator, and the number below the bar is the denominator

CAUTION: The denominator of a fraction can never be 0.

• A fraction such as , in which the numerator is less than the denominator, is called a proper fraction. Its value is less than 1.

• A fraction such as , in which the numerator is more 12 than the denominator, is called an improper fraction. Its value is greater than 1.

• A fraction such as , in which the numerator and denominator are the same, is also an improper fraction, but it is equal to 1.

It is useful to think of the fraction bar as a symbol for division. If three pizzas are divided equally among eight people, each person gets  of a pizza. If you actually use your calculator to divide 3 by 8, you get  = 0.375.

Key Fact B1

Every fraction, proper or improper, can be expressed in decimal form (or as a whole number) by dividing the numerator by the denominator. For example:

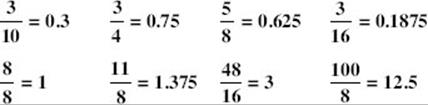
Note: Any number beginning with a decimal point can be written with a 0 to the left of the decimal point. In fact, some calculators will express 3 ÷ 8 as .375, whereas others will print 0.375.

Unlike the examples above, when most fractions are converted to decimals, the division does not terminate after two, three, or four decimal places; rather it goes on forever with some set of digits repeating itself.

On the SAT, you do not need to be concerned with this repetition. On grid-in problems you just enter as much of the number as will fit in the grid; and on multiple-choice questions, all numbers written as decimals terminate.

Although on the SAT you will have occasion to convert fractions to decimals (by dividing), you will not have to convert decimals to fractions.

Calculator Shortcut

On the SAT, never do long division to convert a fraction to a decimal. Use your calculator.

Comparing Fractions and Decimals

Key Fact B2

To compare two decimals, follow these rules:

• Whichever number has the greater number to the left of the decimal point is greater: since 11 > 9, 11.001 > 9.896; and since 1 > 0, 1.234 > 0.8. (Recall that, if a decimal has no number to the left of the decimal point, you may assume that a 0 is there, so 1.234 > .8).

• If the numbers to the left of the decimal point are equal (or if there are no numbers to the left of the decimal point), proceed as follows:

1. If the numbers do not have the same number of digits to the right of the decimal point, add zeros at the end of the shorter one until the numbers of digits are equal.

2. Now, compare the numbers, ignoring the decimal point itself.

For example, to compare 1.83 and 1.823, add 0 at the end of 1.83, forming 1.830. Now, thinking of them as whole numbers, compare the numbers, ignoring the decimal point:

1830 > 1823  1.830 > 1.823.

Key Fact B3

To compare two fractions, use your calculator to convert them to decimals. Then apply KEY FACT B2. This always works.

 For example, to compare  and , write  = 0.3333... and  = 0.375.

Since 0.375 > 0.333,  > .

 CALCULATOR HINT

You can always use your calculator to compare two numbers: fractions, decimals, or integers. By KEY FACT A21, a > b means a – b is positive, and a < b means a – b is negative. Therefore, to compare two numbers, just subtract them. For example,

1.83 – 1.823 = .007  1.83 > 1.823,

.2139 – .239 = –.0251  .2139 < .239,

–6 – (–7) = 1  –6 > –7.

Key Fact B4

When comparing fractions, there are three situations in which it is faster not to use your calculator to convert fractions to decimals (although, of course, that will work).

1. The fractions have the same positive denominator. Then the fraction with the larger numerator is greater. Just as $9 are more than $7, and 9 books are more than 7 books, 9 tenths is more than 7 tenths: .

2. The fractions have the same numerator. Then, if the denominators are positive, the fraction with the smaller denominator is greater. If you divide a cake into five equal pieces, each piece is larger than a piece you would get if you divided the cake into 10 equal pieces: , and similarly .

3. The fractions are so familiar or easy to work with that you already know the answer. 
 For example, and .

Key Fact B5

KEY FACTS B2, B3, and B4 apply to positive decimals and fractions. Clearly, any positive number is greater than any negative number. For negative decimals and fractions, use KEY FACT A25, which states that, if a > b, then –a < –b.

  and .83 > .829  –.83 < –.829

EXAMPLE 1

Which of the following lists the fractions  and in order from least to greatest?

 Solution. On your calculator convert each fraction to a decimal, writing down the first few decimal places:

It is now easy to order the decimals:

0.625 < 0.636 < 0.650 < 0.666.

The answer is (B).

Equivalent Fractions

If Bill and Al shared a pizza, and Bill ate  and Al ate , they had exactly the same amount of the pizza. We express this idea by saying that  and  are equivalent fractions: that is, they have the exact same value.

Note: If you multiply both the numerator and the denominator of  by 4, you get ; and if you divide both the numerator and the denominator of  by 4, you get .

This illustrates the next KEY FACT.

Key Fact B6

Two fractions are equivalent if multiplying or dividing both the numerator and the denominator of the first fraction by the same number gives the second fraction.

Consider the following two cases.

1. Are  and  equivalent? There is a number that, when multiplied by 3 gives 45, and there is a number that, when multiplied by 8, gives 120. By KEY FACT B6, if these numbers are the same, the fractions are equivalent. They are the same number: 3 × 15 = 45 and 8 × 15 = 120.

2. Are  and  equivalent? Since 2 × 14 = 28, but 3 × 14  45, the fractions are not equivalent. Alternatively, 28 ÷ 14 = 2, but 45 ÷ 14  3.

 Calculator Shortcut

To determine whether two fractions are equivalent, convert them to decimals by dividing. For the fractions to be equivalent, the two quotients must be the same.

EXAMPLE 2

Which of the following is NOT equivalent to ?

(A) 

(B) 

(C) 

(D) 

(E) 

 Solution. Since  = 0.625, just check each choice until you find the one that is NOT equal to 0.625. Each of , , , and  is equal to 0.625. Only  (E) does not equal 0.625 .

A fraction is in lowest terms if no positive integer greater than 1 is a factor of both the numerator and the denominator. For example,  is in lowest terms, since no integer greater than 1 is a factor of both 9 and 20; but  is not in lowest terms, since 3 is a factor of both 9 and 24.

Key Fact B7

Every fraction can be reduced to lowest terms by dividing the numerator and the denominator by their greatest common factor (GCF). If the GCF is 1, the fraction is already in lowest terms.

EXAMPLE 3

For any positive integer n, n! means the product of all the integers from 1 to n.
What is the value of  ?

(A) 

(B) 

(C) 

(D) 

(E) 

Solution. Assume that you don’t see the easy way to do this. On your calculator quickly multiply or use the ! key:

             6! = 1·2·3·4·5·6 = 720,

             8! = 1·2·3·4·5·6·7·8 = 40,320.

You are now faced with reducing . Don’t do it; just use your calculator to divide:  = 0.0178..., and now test the choices, starting with C.

 = 0.125, which is too large. Eliminate C as well as D and E, which are even larger, and try A or B. In fact,  = 0.0178.... Choice A is correct. Here’s the easy solution:

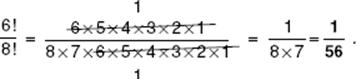
This solution takes only a few seconds, but the calculator solution is simple enough and can surely be done in less than a minute.

Arithmetic Operations with Decimals

On the SAT, all decimal arithmetic (including whole numbers) that you can’t easily do in your head should be done on your calculator. This shortcut saves time and avoids careless errors. If you know that 12 × 12 = 144 and that 1.2 × 1.2 = 1.44, fine; but if you’re not sure, use your calculator rather than your pencil. You should even use your calculator to multiply 0.2 × 0.2 if there’s any chance that you would get 0.4 instead of 0.04 as the answer.

Helpful Hint

Any whole number can be treated as a decimal: 7 = 7.0.

You should not have to use your calculator to multiply or divide any decimal number by a power of 10, because multiplying and dividing by 10 or 100 or 1000 is a calcuation you should be able to do easily in your head.

Key Fact B8

To multiply any decimal or whole number by a power of 10, move the decimal point as many places to the right as there are 0’s in the power of 10, filling in with 0’s if necessary.

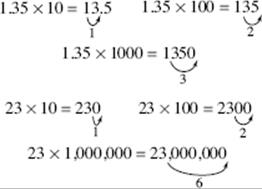
Key Fact B9

To divide any decimal or whole number by a power of 10, move the decimal point as many places to the left as there are 0’s in the power of 10, filling in with 0’s if necessary.

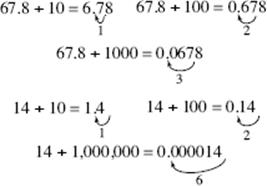
On the SAT, you never have to round off decimal answers. On grid-ins just enter the number, putting in as many digits after the decimal point as fit. For example, enter 3.125 as  and .1488 as  . However, you do have to know how to round off, because occasionally there is a question about that procedure.

Key Fact B10

To round off a decimal number to any place, follow these rules, which are fully explained with examples in the table below.

• Keep all of the digits to the left of the specified place.

• In that place, keep the digit if the next digit is < 5, and increase that digit by 1 if the next digit is  5. (Note: 9 increased by 1 is 10: put down the 0 and carry the 1.)

• If there are still digits to the left of the decimal point, change them to 0’s and eliminate the decimal point and everything that follows it.

• If you are at or beyond the decimal point, stop: don’t write any more digits.

For example, here is how to round off 3815.296 to any place.

Round to the Nearest:	Procedure	Answer
thousand	The digit in the thousands place is 3; since the next digit (8) is ≥ 5, increase the 3 to a 4; fill in the 3 places to the left of the decimal point with 0’s.	4000
hundred	The digit in the hundreds place is 8; keep everything to the left of it, and keep the 8 since the next digit (1) is < 5; fill in 0’s to the left of the decimal point.	3800
ten	The digit in the tens place is 1; keep everything to the left of it, and increase the 1 to a 2 since the next digit (5) is ≥ 5; fill in 0’s to the left of the decimal point.	3820
one	The digit in the ones place is 5; keep everything to the left of it, and keep the 5 since the next digit (2) is < 5; there are no more places to the left of the decimal point, so stop.	3815
tenth	The digit in the tenths place is 2; keep everything to the left of it, and increase the 2 to a 3 since the next digit (9) is ≥ 5; you are beyond the decimal point, so stop.	3815.3
hundredth	The digit in the hundredths place is 9; keep everything to the left of it, and, since the next digit (6) is ≥ 5, increase the 9 to a 10; put down the 0 and carry a 1 into the tenths place: 0.29 becomes 0.30; since you are beyond the decimal point, stop.	3815.30

EXAMPLE 4

When 423,890 is rounded off to the nearest thousand, how many digits will be changed?

(A) 0

(B) 1

(C) 2

(D) 3

(E) 4

Solution. When 423,890 is rounded off to the nearest thousand, 3 digits are changed: 424,000 (D).

Arithmetic Operations with Fractions

Key Fact B11

To multiply two fractions, multiply their numerators and multiply their denominators.

Key Fact B12

To multiply a fraction by any other number, write that number as a fraction whose denominator is 1.

TACTIC B1

Before multiplying fractions, reduce. You may reduce by dividing any numerator and any denominator by a common factor.

EXAMPLE 5

Express the product  in lowest terms.

Solution. If you just multiply the numerators and denominators (with a calculator, of course), you get , which is a nuisance to reduce. Also, dividing on your calculator won’t help, since your answer is supposed to be a fraction in lowest terms. It is better to use TACTIC B1 and reduce first:

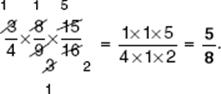
TACTIC B2

When a problem requires you to find a fraction of a number, multiply.

EXAMPLE 6

If  of the 350 sophomores at Adams High School are girls, and  of the girls play on a team, how many sophomore girls do NOT play on a team?

 Solution. There are  × 350 = 200 sophomore girls.

Of these, × 200 = 175 play on a team. Then, 200 – 175 = 25 do not play on a team.

How should you multiply  × 350? If you can do this mentally, you should:

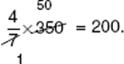
The next step, however, requires you to multiply  by 200, and more likely than not you don’t immediately see that 200 divided by 8 is 25 or that 7 times 25 equals 175:

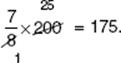
For any step that you can’t do instantly, you should use your calculator:

(4 ÷ 7) × 350 × (7 ÷ 8) = 175.

 CALCULATOR HINT

If you are going to use your calculator on a problem, don’t bother reducing anything. Given the choice of multiplying  × 80 or  × 80, you would prefer the second option, but for your calculator the first one is just as easy.

The reciprocal of any nonzero number, x, is the number . The reciprocal of the fraction  is the fraction .

Key Fact B13

To divide any number by a fraction, multiply the number by the reciprocal of the fraction.

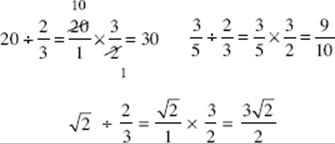
EXAMPLE 7

In the meat department of a supermarket, 100 pounds of chopped meat was divided into packages, each of which weighed  pound. How many packages were there?

Solution. 100 ÷ 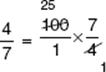 = 175.

Key Fact B14

To add or subtract fractions with the same denominator, add or subtract the numerators and keep the denominator.

To add or subtract fractions with different denominators, first rewrite the fractions as equivalent fractions with the same denominator.

Note: The easiest denominator to find is the product of the denominators (6 × 4 = 24, in this example), but the best denominator to use is the least common denominator, which is the least common multiple (LCM) of the denominators (12 in this case). Using the least common denominator minimizes the amount of reducing that is necessary to express the answer in lowest terms.

Key Fact B15

If  is the fraction of the whole that satisfies some property, then 1 – is the fraction of the whole that does not satisfy it.

EXAMPLE 8

In a jar,  of the marbles are red,  are white, and  are blue. What fraction of the marbles are neither red, white, nor blue?

Solution. The red, white, and blue marbles constitute

of the total, so

of the marbles are neither red, white, nor blue.

EXAMPLE 9

Ali ate  of a cake and Jason ate  of it. What fraction of the cake was still uneaten?

EXAMPLE 10

Ali ate  of a cake and Jason ate  of what was left. What fraction of the cake was still uneaten?

CAUTION: Be sure to read questions carefully. In Example 9, Jason ate  of the cake. In Example 10, however, he ate only  of the  that was left after Ali had her piece.

He ate

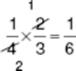
of the cake.

Solution 9.  of the cake was eaten, and  was uneaten.

Solution 10.  of the cake was eaten, and the other  was uneaten.

Arithmetic Operations with Mixed Numbers

A mixed number is a number, such as 3, that consists of an integer followed by a fraction.

The mixed number is an abbreviation for the sum of the integer and the fraction; so 3 is an abbreviation for 3 + .

Every mixed number can be written as an improper fraction, and every improper fraction can be written as a mixed number:

                 and    

Key Fact B16

To write a mixed number as an improper fraction, or an improper fraction as a mixed number, follow these rules:

1. To write a mixed number  as an improper fraction, multiply the whole number (3) by the denominator (2), add the numerator (1), and write the sum over the denominator (2): .

2. To write an improper fraction  as a mixed number, divide the numerator by the denominator; the quotient (3) is the whole number.

    Place the remainder (1) over the denominator to form the fractional part .

CAUTION: You can never grid in a mixed number. You must change it to an improper fraction or a decimal.

Helpful Hint

Understanding the procedures in Key Facts B17, B18, and B19 will help you avoid careless mistakes. However, any arithmetic that you can’t do in your head, you should do on your calculator.

Key Fact B17

To add mixed numbers, add the integers and also add the fractions.

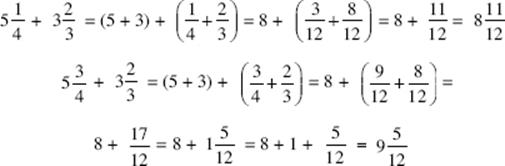
Key Fact B18

To subtract mixed numbers, subtract the integers and also subtract the fractions. If, however, the fraction in the second number is greater than the fraction in the first number, you first have to borrow 1 from the integer part.

For example, since , you can’t subtract  until you borrow 1 from the 5:

Now, you have

Key Fact B19

To multiply or divide mixed numbers, change them to improper fractions.

CAUTION: Be aware that  is not 15; rather:

Complex Fractions

A complex fraction is a fraction, such as , that has one or more fractions in its numerator or denominator or both.

Key Fact B20

There are two ways to simplify a complex fraction:

1. Multiply every term in the numerator and denominator by the least common multiple of all the denominators that appear in the fraction.

2. Simplify the numerator and the denominator, and divide.

To simplify , multiply each term by 12, the LCM of 6 and 4:

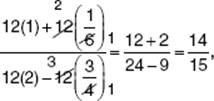
or write

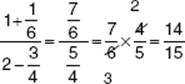
 Calculator Shortcut

Remember that, on the SAT, if you ever get stuck on a fraction problem, you can always convert the fractions to decimals and do all the work on your calculator.

Exercises on Fractions and Decimals

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

1. A French class has 12 boys and 18 girls. Boys are what fraction of the class?

(A) 

(B) 

(C) 

(D) 

(E) 

2. For how many integers, a, between 30 and 40 is it true that , , and  are all in lowest terms?

(A) 1

(B) 2

(C) 3

(D) 4

(E) 5

3.  is the average (arithmetic mean) of  and what number?

(A) 

(B) 

(C) 

(D) 

(E) 

4. If  of a number is 22, what is  of that number?

(A)   6

(B) 11

(C) 12

(D) 33

(E) 44

5. What fractional part of a week is 98 hours?

(A) 

(B) 

(C) 

(D) 

(E) 

6.  of 24 is equal to  of what number?

(A)   7

(B)   8

(C) 15

(D) 

(E) 

7. Which of the following is less than ?

(A) 

(B) 

(C) 

(D) 

(E) .565

8. Which of the following is (are) greater than x when x = ?

  I. 

 II. 

III. 

(A) I only

(B) I and II only

(C) I and III only

(D) II and III only

(E) I, II, and III

9. Which of the following statements is true?

(A) 

(B) 

(C) 

(D) 

(E) 

10. If a = 0.99, which of the following is (are) less than a?

  I. 

 II. a²

III. 

(A) None

(B) I only

(C) II only

(D) III only

(E) II and III only

11. For the final step in a calculation, Paul accidentally divided by 1000 instead of multiplying by 1000. What should he do to his answer to correct it?

(A) Multiply it by 1000.

(B) Multiply it by 100,000.

(C) Multiply it by 1,000,000.

(D) Square it.

(E) Double it.

Grid-in Questions

12. One day at Central High School,  of the students were absent, and  of those present went on a field trip. If the number of students staying in school was 704, how many students are enrolled at Central High?

13. What is a possible value of x if ?

14. If 7a = 3 and 3b = 7, what is the value of ?

15. If A = {1, 2, 3}, B = {2, 3, 4}, and C is the set consisting of all the fractions whose numerators are in A and whose denominators are in B, what is the product of all of the numbers in C?

Answer Key

1. A 2. C 3. B 4. E

5. E 6. A 7. D 8. B

9. B 10. C 11. C

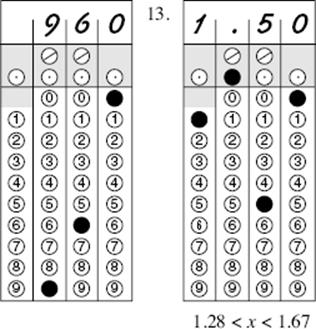
12. 

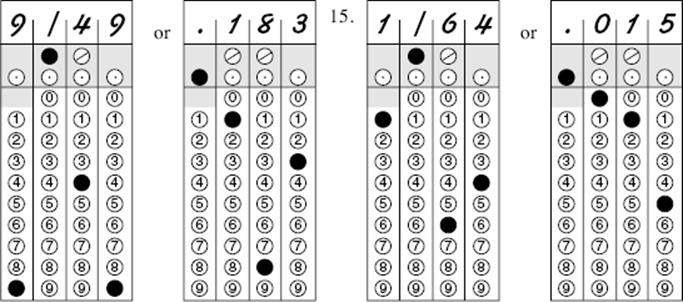
14. 

Answer Explanations

1. (A). The class has 30 students, of whom 12 are boys. The boys make up  of the class.

2. (C). If a is even, then  is not in lowest terms, since both a and 8 are divisible by 2. The only possibilities are 31, 33, 35, 37, and 39, but , and , so only 31, 33, and 37 (that is, 3 integers) remain.

3. (B). The average of  and another number, x, is

Multiplying both sides by 2 yields .

4. (E). Don’t bother writing an equation for this one; just think. You know that  of the number is 22, and  of a number is twice as much as  of it: 2 × 22 = 44.

5. (E). There are 24 hours in a day and 7 days in a week, so there are 24 × 7 = 168 hours in a week: .

6. (A). If x is the number,

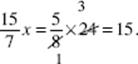
Then, , which means (dividing by 15) that , so x = 7.

7. (D).  Use your calculator:  = 0.5555555.…; Choice C is also equal to 0.555555...; choices A, B, and E are all greater; only  = 0.55 is less.

8. (B). • The reciprocal of a number less than 1 is greater than 1. (I is true).

• , which is greater than 1. (II is true).

• When , x + 1 is positive, whereas x – 1 is negative. Then  is negative, and hence less than 1. (III is false.)

9. (B).  Use your calculator to convert each fraction to a decimal:

 = 0.3636…,  = 0.375,  = 0.3846….

This is the correct order.

10. (C). • Since a < 1, then  > a. (I is false.)

• Since a < 1, then a² < a. (II is true.)

• The reciprocal of a number less than 1 is greater than 1. (III is false.)

11. (C). Multiplying the incorrect answer by 1000 would undo the final division Paul made—the point at which he should have multiplied by 1000. Then, to correct his error, he would have to multiply again by 1000. In all, he should multiply by 1000 × 1000 = 1,000,000.

12. (960) If s is the number of students enrolled,  is the number who were absent, and  is the number who were present. Since  of those present went on a field trip,  of them stayed in school. Therefore,

.

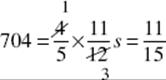
13. (1.28 < x < 1.67) Since  = .6 and  = .777…,  can be any number between .6 and .777. If  = .7 = , then x =  = or 1.42; if  = .75 = , then x =  or 1.33; and so on.

14.  Since 7a = 3 and 3b = 7, then . So

 or .183.

15.  Nine fractions are formed:

When you multiply, the three 2’s and the three 3’s in the numerators cancel with the three 2’s and three 3’s in the denominators. Then, the numerator is 1 and the denominator is 4 × 4 × 4 = 64. Grid in  or .015.

9-C Percents

The word percent means “hundredth.” The symbol “%” is used to express the word percent. For example, “17 percent” means “17 hundredths” and can be written with a % symbol, as a fraction, or as a decimal:

Helpful Hint

A percent is just a fraction whose denominator is 100: .

Key Fact C1

To convert a percent to a decimal, or a percent to a fraction, follow these rules:

1. To convert a percent to a decimal, drop the % symbol and move the decimal point two places to the left, adding 0’s if necessary. (Remember: it is assumed that there is a decimal point to the right of any whole number.)

2. To convert a percent to a fraction, drop the % symbol, write the number over 100, and reduce.

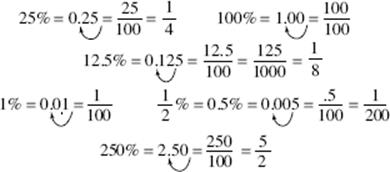
Key Fact C2

To convert a decimal to a percent, or a fraction to a percent, follow these rules:

1. To convert a decimal to a percent, move the decimal point two places to the right, adding 0’s if necessary, and add the % symbol.

2. To convert a fraction to a percent, first convert the fraction to a decimal, then do step 1.

You should be familiar with the following basic conversions:

Knowing these conversions can help you to solve many problems more quickly. For example, the fastest way to find 25% of 32 is to know that 25% = , and that  of 32 is 8, not to use your calculator.

 It is important to keep in mind, however, that any problem involving percents can be done on your calculator: to find 25% of 32, write 25% as a decimal and multiply: 32 × .25 = 8. Here is another example of mental math being much faster than calculator math. Since 10% = , to take 10% of a number, just divide by 10 by moving the decimal point one place to the left: 10% of 60 is 6. Also, since 5% is half of 10%, then 5% of 60 is 3 (half of 6); and since 30% is 3 times 10%, then 30% of 60 is 18 (3 × 6).

Practice this shortcut, because improving your ability to do mental math will add valuable points to your score on the SAT.

Solving Percent Problems

Now, consider these three questions:

  (i) What is 45% of 200?

 (ii) 90 is 45% of what number?

(iii) 90 is what percent of 200?

Each question can be answered easily by using your calculator, but you must first set the question up properly so that you know what to multiply or divide. In each case, there is one unknown; call it x. Now, just translate each sentence, replacing “is” by “=” and the unknown by x.

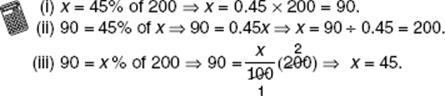
Many students have been taught to answer questions such as these by writing this proportion:

To use this method, think of is, of, and percent as variables. In each percent problem you are given two variables and asked to find the third, which you label x. Of course, you then solve the equation by cross-multiplying.

For example, the three problems solved above could be handled as follows:

(i) What is 45% of 200? (Let x = the is number.)

(ii) 90 is 45% of what number? (Let x = the of number.)

(iii) 90 is what % of 200? (Let x = the percent.)

EXAMPLE 1

Brian gave 20% of his baseball cards to Scott and 15% to Adam. If he still had 520 cards, how many did he have originally?

 Solution. Originally, Brian had 100% of the cards (all of them). After he gave away 35% of them, he had 100% – 35% = 65% of them left. Then 520 is 65% of what number?

520 = .65x  x = 520 ÷ .65 = 800

EXAMPLE 2

After Michael gave 110 baseball cards to Sally and 75 to Heidi, he had 315 left. What percent of his cards did Michael give away?

 Solution. Michael gave away a total of 185 cards and had 315 left. Therefore, he started with 185 + 315 = 500 cards. Then 185 is what percent of 500?

Michael gave away 37% of his cards.

Since percent means “hundredth,” the easiest number to use in any percent problem is 100:

Key Fact C3

For any positive number a: a% of 100 is a.

For example, 11.2% of 100 is 11.2; 500% of 100 is 500; and % of 100 = .

TACTIC C1

In any problem involving percents, use the number 100.

EXAMPLE 3

In 1970 the populations of town A and town B were the same. From 1970 to 1980, however, the population of town A increased by 60% while the population of town B decreased by 60%. In 1980, the population of town B was what percent of the population of town A?

(A) 25%

(B) 36%

(C) 40%

(D) 60%

(E) 120%

Solution. In your math class, you would let x be the population of town A in 1970 and then proceed to set up an algebra problem. Don’t do that on the SAT. Assume that the populations of both towns were 100 in 1970. Then, since 60% of 100 is 60, in 1980 the populations were 100 + 60 = 160 (town A) and 100 – 60 = 40 (town B). Then, in 1980, town B’s population was  of town A’s. Choice A is correct.

Since a% of b is , and b% of a is , KEY FACT C4 follows.

Key Fact C4

For any positive numbers a and b: a% of b = b% of a.

Percent Increase and Decrease

Helpful Hint

Be sure to learn KEY FACT C5. It is very important.

Key Fact C5

The percent increase of a quantity is .

The percent decrease of a quantity is .

For example:

• If the price of a DVD player rises from $80 to $100, the actual increase is $20, and the percent increase is

• If a $100 DVD player is on sale for $80, the actual decrease in price is $20, and the percent decrease is

Note that the percent increase in going from 80 to 100 is not the same as the percent decrease in going from 100 to 80.

Key Fact C6

If a < b, the percent increase in going from a to b is always greater than the percent decrease in going from b to a.

Key Fact C7

• To increase a number by k %, multiply it by (1 + k %).

• To decrease a number by k %, multiply it by (1 – k %).

For example:

• The value of a $1600 investment after a 25% increase is $1600(1 + 25%) = $1600(1.25) = $2000.

• If the investment then loses 25% of its value, it is worth $2000(1 – 25%) = $2000(.75) = $1500.

Note that, after a 25% increase followed by a 25% decrease, the value is $1500, $100 less than the original amount.

EXAMPLE 4

From 2003 to 2004, the number of applicants to a college increased 15% to 5060. How many applicants were there in 2003?

(A) 759

(B) 4301

(C) 4400

(D) 5819

(E) 5953

 Solution. The number of applicants in 2003 was 5060 ÷ 1.15 = 4400 (C).

Note: Some students find percent problems like Example 4 to be harder than other types. Now, you should be able to solve them correctly. If, however, you get stuck on a problem like this on the SAT, you still should answer it. In Example 4, since the number of applicants increased from 2003 to 2004, the number in 2003 was clearly fewer than 5060, so eliminate D and E. Also, 759 (A) is much too small, leaving only B and C as reasonable choices. Therefore, do not omit the question—guess. This situation, in which some of the choices are absurd, is commonplace on the SAT. (See TACTIC 8.)

 Calculator Shortcut

If a number is the result of increasing another number by k%, then, to find the original number, divide by (1 + k%). Also, if a number is the result of decreasing another number by k%, then to find the original number, divide it by (1 – k%).

CAUTION: Percents over 100%, which come up most often on questions involving percent increases, are confusing for many students. Be sure you understand that 100% of a particular number is that number, 200% of a number is 2 times the number, and 1000% of a number is 10 times the number. For example, if the value of an investment rises from $1000 to $5000, the investment is now worth 5 times, or 500%, as much as it was originally; but there has been only a 400% increase in value:

EXAMPLE 5

The population of a town doubled every 10 years from 1960 to 1990. What was the percent increase in population during this time?

Solution. The population doubled 3 times from, say, 100 to 200 to 400 to 800. Therefore, the population in 1990 was 8 times the population in 1960, but this was an increase of 700 people, or 700%.

Exercises on Percents

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

  1. Charlie bought a $60 radio on sale at 5% off. How much did he pay, including 5% sales tax?

(A) $54.15

(B) $57.00

(C) $57.75

(D) $59.85

(E) $60.00

  2. If a is a positive number, 400% of a is what percent of 400a?

(A) 0.01

(B) 0.1

(C) 1

(D) 10

(E) 100

  3. What percent of 50 is b?

  4. At Harry’s Discount Hardware everything is sold for 20% less than the price marked. If Harry buys tool kits for $80, what price should he mark them if he wants to make a 20% profit on his cost?

(A) $96

(B) $100

(C) $112

(D) $120

(E) $125

  5. 9 is % of what number?

(A) 0.03

(B) .27

(C) 3

(D) 300

(E) 2700

  6. Mr. Howard was planning on depositing a certain amount of money each month into a college fund for his children. He then decided not to make any contributions during June and July. To make the same annual contribution that he had originally planned, by what percent should he increase his monthly deposits?

(A) 

(B) 20%

(C) 25%

(D) 

(E) It cannot be determined from the information given.

  7. During his second week on the job, Jason earned $110. This represented a 25% increase over his earnings of the previous week. How much did he earn during his first week of work?

(A) $82.50

(B) $85.00

(C) $88.00

(D) $137.50

(E) $146.67

  8. What is 10% of 20% of 30%?

(A) 0.006%

(B) 0.6%

(C) 6%

(D) 60%

(E) 6000%

  9. If 1 micron = 10,000 angstroms, then 100 angstroms is what percent of 10 microns?

(A) 0.0001%

(B) 0.001%

(C) 0.01%

(D) 0.1%

(E) 1%

10. On a test consisting of 80 questions, Marie answered 75% of the first 60 questions correctly. What percent of the other 20 questions did she need to answer correctly for her grade on the entire exam to be 80%?

(A) 85%

(B) 87.5%

(C) 90%

(D) 95%

(E) 100%

Grid-in Questions

11. A jar contains 2000 marbles. If 61.5% of them are red, 27.2% of them are white, and 10% of them are blue, how many are neither red, white, nor blue?

12. If 25 students took an exam and 4 of them failed, what percent of them passed?

13. There are twice as many girls as boys in an English class. If 30% of the girls and 45% of the boys have already handed in their book reports, what percent of the students have not yet handed in their reports?

14. During a sale a clerk was putting a new price tag on each item. On one radio, he accidentally raised the price by 15% instead of lowering the price by 15%. As a result the price on the tag was $45 too high. What was the original price, in dollars, of the radio?

15. If a person has an income of $100,000, what percent of his income does he pay in federal income tax if the tax rate is as given below?

15% of the first $30,000 of income,

28% of the next $30,000 of income, and

31% of all income in excess of $60,000.

16. The price of a can of soup was increased by 20%. How many cans can be purchased for the amount of money that used to buy 300 cans?

17. An art dealer bought a painting for $1000 and later sold it for $10,000. By what percent did the value of the painting increase?

18. Jar B has 20% more marbles than jar A. What percent of the marbles in jar B have to be moved to jar A, in order that the number of marbles in each jar will be the same?

19. Wendy drew a square. She then erased it and drew a second square whose sides were 3 times the sides of the first square. The area of the second square is k% greater than the area of the first square. What is k?

20. In a large jar full of jelly beans, 30% of them are red, and 40% of the red jelly beans are cherry. If 25% of the non-cherry-flavored red jelly beans are raspberry, what percent of all the jelly beans are either cherry or raspberry?

Answer Key

1. D   2. C   3. E   4. D

5. E   6. B   7. C   8. B

9. D 10. D

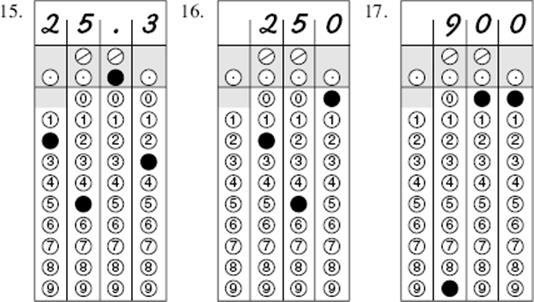
Answer Explanations

  1. (D).     Since 5% of 60 is 3, Charlie saved $3, and thus paid $57 for the radio. He then had to pay 5% sales tax on the $57: .05 × 57 = 2.85, so the total cost was $57 + $2.85 = $59.85.

  2. (C).    400% of a = 4a, which is 1% of 400a.

  3. (E).    If b is x% of 50, then .

  4. (D).     Since 20% of 80 is 16, Harry wants to get $96 for each tool kit he sells. What price should the tool kits be marked so that, after a 20% discount, the customer will pay $96? If x represents the marked price, then .

  5. (E).    .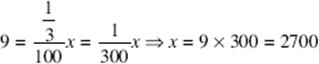

  6. (B).    Assume that Mr. Howard was going to contribute $100 each month, for an annual total of $1200. Having decided not to contribute for 2 months, he would have to contribute the $1200 in 10 monthly deposits of $120 each. This is an increase of $20, and a percent increase of 

  7. (C).     To find Jason’s earnings during his first week, divide his earnings of the second week by 1.25: $110 ÷ 1.25 = $88.

**If you let x represent Jason’s earnings during the first week, then x + 0.25x = 110  1.25x = 110, and so, as above, x = 110 ÷ 1.25 = 88.

  8. (B).     10% of 20% of 30% = .10 × .20 × .30 = 0.006 = 0.6%.

  9. (D).    1 micron = 10,000 angstroms  10 microns = 100,000 angstroms; then, dividing both sides by 1000 gives 100 angstroms = (10 microns); and = 0.001 = 0.1%.

10. (D).     To earn 80% on the entire exam, Marie needs to correctly answer 64 questions (80% of 80). So far, she has answered 45 questions correctly (75% of 60). Therefore, on the last 20 questions she needs 64 – 45 = 19 correct answers; and  = 95%.

11. (26)     Since 61.5 + 27.2 + 10 = 98.7, then 98.7% of the marbles are red, white, or blue, and the other 100% – 98.7% = 1.3% are some other colors. Therefore: 1.3% of 2000 = 0.013 × 2000 = 26.

12. (84)     If 4 of the 25 students failed, then the other 21 students passed, and  = 0.84 = 84%.

13. (65)     Assume that there are 100 boys and 200 girls in the class. Then, 45 boys (45% of 100) and 60 girls (30% of 200) have handed in their reports. Then, 105 of the 300 students have handed in the reports, and 300 – 105 = 195 have not. What percent of 300 is 195?

 = 0.65 = 65%.

14. (150)     If p represents the original price, the radio was priced at 1.15p instead of .85p. Since this was a $45 difference: 45 = 1.15p – .85p = 0.30p  p = 45 ÷ .30 = 150.

15. (25.3)     A person with a $100,000 income would pay 15% of $30,000 plus 28% of $30,000 plus 31% of $40,000:

   (.15 × 30,000) + (.28 × 30,000) + (.31 × 40,000) = 4,500 + 8,400 + 12,400 = 25,300 and 25,300 is 25.3% of 100,000.

16. (250)     Assume that a can of soup used to cost $1 and that it now costs $1.20 (20% more). Then 300 cans of soup used to cost $300. How many cans costing $1.20 each can be bought for $300?

300 ÷ 1.20 = 250.

17. (900)    The increase in the value of the painting was $9000, and

                  

18.     Assume that there are 100 marbles in jar A and 120 in jar B. You may already see that, if 10 marbles are moved, each jar will contain 110. If not, let x be the number of marbles to be moved, and solve the equation: 120 – x = 100 + x  20 = 2x  x = 10. Finally, 10 is what percent of 120? 

19. (800)    Assume that the sides of the first square were 1 inch long, so that the area was 1 square inch. Then, the sides of the second square were 3 inches long, and its area was 9 square inches, an increase of 8 square inches or 800%.

20. (16.5)    Since 40% of the red jelly beans are cherry, 60% of the red jelly beans are not cherry. Also, 25% of 60% is 15%, so 15% of the red jelly beans are raspberry and 40% are cherry, for a total of 55%. Therefore, the raspberry and cherry jelly beans constitute 55% of the 30% of the jelly beans that are red. Finally, 55% of 30% is 16.5%.

9-D Ratios and Proportions

A ratio is a fraction that compares two quantities that are measured in the same units. One quantity is the numerator of the fraction, and the other quantity is the denominator.

For example, if there are 4 boys and 16 girls on the debate team, the ratio of the number of boys 4 to the number of girls on the team is 4 to 16, or , often written as 4:16. Since a ratio is a 16 fraction, it can be reduced or converted to a decimal or a percent. The following are different ways to express the same ratio:

Helpful Hint

Remember that ratios can always be written as fractions.

CAUTION: Saying that the ratio of boys to girls on the team is 1:4 does not mean  that of the team members are boys. It means that, for each boy on the team there are 4 girls, so, of every 5 members of the team, 4 are girls and 1 is a boy. Boys, therefore, make  up of the team, and girls 

Key Fact D1

If a set of objects is divided into two groups in the ratio of a:b, then the first group contains  of the objects and the second group contains  of the objects.

EXAMPLE 1

Last year, the ratio of the number of math tests John passed to the number of math tests he failed was 7:3. What percent of his math tests did John pass?

Solution. John passed  of his math tests.

EXAMPLE 2

If 45% of the students at a college are male, what is the ratio of male students to female students?

Reminder: In problems involving percents, the best number to use is 100.

Solution. Assume that there are 100 students. Then, 45 of them are male, and 55 of them (100 – 45) are female.

The ratio of males to females is 

If we know how many boys and girls there are in a club, then, clearly, we know not only the ratio of boys to girls, but also several other ratios. For example, if the club has 7 boys and 3 girls, the ratio of boys to girls is  the ratio of girls to boys is  the ratio of boys to members is  the ratio of members to girls is , and so on.

However, if we know a ratio, we cannot determine from that fact alone how many objects there are. For example, if a jar contains only red and blue marbles, and if the ratio of red marbles to blue marbles is 3:5, there may be 3 red marbles and 5 blue marbles, but not necessarily. There may be 300 red marbles and 500 blue ones, since the ratio 300:500 reduces to 3:5. In the same way, all of the following are possibilities for the distribution of the marbles:

Red	6	12	33	51	150	3000	3x
Blue	10	20	55	85	250	5000	5x

The important thing to observe is that the number of red marbles can be any multiple of 3, as long as the number of blue marbles is the same multiple of 5.

Key Fact D2

If two numbers are in the ratio of a:b, then, for some number x, the first number is ax and the second number is bx. If the ratio is in lowest terms, and if the quantities must be integers, then x is also an integer.

TACTIC D1

In any ratio problem, write the letter x after each number and use some given information to solve for x.

EXAMPLE 3

If the ratio of boys to girls at a school picnic is 5:3, which of the following CANNOT be the number of children at the picnic?

(A) 24

(B) 40

(C) 96

(D) 150

(E) 720

Solution. If 5x and 3x are the number of boys and the number of girls, respectively, at the picnic, then the number of children present is 5x + 3x = 8x. Therefore, the number of children must be a multiple of 8. Only 150 (D) is not divisible by 8.

Note: Assume that the ratio of the number of pounds of cole slaw to the number of pounds of potato salad consumed at the school picnic was 5:3. Then, it is possible that a total of exactly 150 pounds of these foods was eaten: 93.75 pounds of cole slaw and 56.25 pounds of potato salad. In Example 3, however, 150 isn’t a possible answer because there has to be a whole number of boys and girls.

EXAMPLE 4

The measures of the two acute angles of a right triangle are in the ratio of 5:13. What is the measure of the larger acute angle?

Solution. Let the measure of the smaller angle be 5x and the measure of the larger angle be 13x. Since the sum of the measures of the two acute angles of a right triangle is 90% (KEY FACT J3):

5x + 13x = 90  18x = 90  x = 5.

Therefore, the measure of the larger angle is 13 × 5 = 65°.

Ratios can be extended to three or four or more terms. For example, we can say that the ratio of freshmen to sophomores to juniors to seniors in the school band is 6:8:5:8, which means that for every 6 freshmen in the band there are 8 sophomores, 5 juniors, and 8 seniors.

Note: TACTIC D1 applies to extended ratios, as well.

EXAMPLE 5

Frannie’s Frozen Yogurt sells three flavors: vanilla, chocolate, and coffee. One day, Frannie sold 240 cones, and the ratio of vanilla to chocolate to coffee was 8:17:15. How many chocolate cones were sold that day?

Solution. Let 8x, 17x, and 15x be the number of vanilla, of chocolate, and of coffee cones sold, respectively. Then:

8x + 17x + 15x = 240  40x = 240  x = 6.

The number of chocolate cones sold was 17 × 6 = 102.

Key Fact D3

KEY FACT D1 applies to extended ratios, as well. If a set of objects is divided into three groups in the ratio a:b:c, then the first group contains  of the objects, the second , and the third 

EXAMPLE 6

If the ratio of vanilla to chocolate to coffee cones sold at Frannie’s was 8:17:15 on a particular day, what percent of the cones sold were chocolate?

 Solution. Chocolate cones made up  of the total.

A jar contains a number of red (R), white (W), and blue (B) marbles. Suppose that R:W = 2:3 and W:B = 3:5. Then, for every 2 red marbles, there are 3 white ones, and for those 3 white ones, there are 5 blue ones. Then, R:B = 2:5, and we can form the extended ratio R:W:B = 2:3:5.

If the ratios were R:W = 2:3 and W:B = 4:5, however, we couldn’t combine them as easily. From the diagram below, we see that for every 8 reds there are 15 blues, so R:B = 8:15.

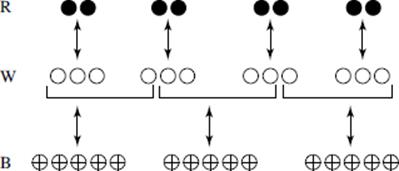
To see this without drawing a picture, we write the ratios as fractions: 

Then, we multiply the fractions:

Not only does this give us R:B = 8:15, but also, if we multiply both W numbers, 3 × 4 =12, we can write the extended ratio: R:W:B = 8:12:15.

EXAMPLE 7

Jar A and jar B each contain 70 marbles, all of which are red, white, or blue.

In jar A, R:W = 2:3 and W:B = 3:5.
In jar B, R:W = 2:3 and W:B = 4:5.

What is the total number of white marbles in the two jars?

Solution. From the discussion immediately preceding this example, in jar A the extended ratio = R:W:B is 2:3:5, which implies that the white marbles constitute  of the total:

In jar B the extended ratio R:W:B is 8:12:15, so the white marbles are  of the total:

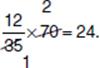
Finally, there is a total of 21 + 24 = 45 white marbles.

A proportionis an equation that states that two ratios are equivalent. Since ratios are just fractions, any equation, such as  in which each side is a single fraction is a proportion. Usually the proportions encountered on the SAT involve one or more variables.

TACTIC D2

Solve proportions by cross-multiplying: if  then ad = bc. Several problems on the SAT can be solved by setting up proportions. These problems are usually quite easy and are among the first few in a section.

EXAMPLE 8

   If  what is the value of x?

 Solution. Cross-multiply: 3(84) = 7x  252 = 7x  x = 36.

EXAMPLE 9

   If  what is the value of ? 

Solution. Cross-multiply: 16(x + 2) = 17x  16x + 32 = 17x  x = 32, so

EXAMPLE 10

A state law requires that on any field trip the ratio of the number of chaperones to the number of students must be at least 1:12. If 100 students are going on a field trip, what is the minimum number of chaperones required?

 Solution. Let x represent the number of chaperones required, and set up a proportion:

Cross-multiply: 100 = 12x  x = 8.33. This, of course, is not the answer since, clearly, the number of chaperones must be a whole number. Since x is greater than 8, you know that 8 chaperones will not be enough. The answer is 9.

A rate is a fraction that compares two quantities that are measured in different units. The word per often appears in rate problems: miles per hour, dollars per week, cents per ounce, children per classroom, and so on.

TACTIC D3

Set rate problems up just like ratio problems. Then, solve the proportions by cross-multiplying.

EXAMPLE 11

Sharon read 24 pages of her book in 15 minutes. At this rate, how many pages can she read in 40 minutes?

 Solution. Handle this rate problem exactly like a ratio problem. Set up a proportion and cross-multiply:

When the denominator in the given rate is 1 unit (1 minute, 1 mile, 1 dollar), the problem can be solved by a single division or multiplication. Consider Examples 12 and 13.

EXAMPLE 12

If Jack types at the rate of 35 words per minute, how long will he take to type 987 words?

EXAMPLE 13

If Jack types at the rate of 35 words per minute, how many words can he type in 85 minutes?

To solve, set up the proportions and cross-multiply.

 Solution 12.  minutes.

 Solution 13.  words.

Notice that, in Example 12, all that was done was to divide 987 by 35, and in Example 13, 35 was multiplied by 85. If you realize that, you don’t have to introduce x and set up a proportion. You must know, however, whether to multiply or divide. If you’re not absolutely positive which is correct, write the proportion; then you can’t go wrong.

CAUTION: In rate problems it is essential that the units in both fractions be the same.

EXAMPLE 14

If three apples cost 50¢, how many apples can you buy for $20?

Solution. You have to set up a proportion, but it is not  In the first fraction, the denominator represents cents, whereas in the second fraction, the denominator represents dollars. The units must be the same. You can change 50 cents to 0.5 dollar, or you can change 20 dollars to 2000 cents:

On the SAT, many rate problems involve only variables. These problems are handled in exactly the same way.

EXAMPLE 15

If a apples cost c cents, how many apples can be bought for d dollars?

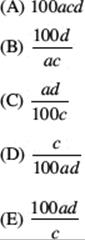
Solution. First change d dollars to 100d cents; then set up the proportion and cross-multiply:

Every SAT has one or two questions like Example 15, and most students find them very difficult. Be sure to do all the exercises at the end of this section, but also see TACTIC 6 in Chapter 8 for another way to handle these problems.

Notice that in rate problems, as one quantity increases or decreases, so does the other. If you are driving at 45 miles per hour, the more hours you drive, the further you go; if you drive fewer miles, less time is required.

Rate problems are examples of direct variation. We say that one variable is directly proportional to a second variable if their quotient is a constant. If y is directly proportional to x, there is a constant k, such that 

When two quantities vary directly, as one quantity increases (or decreases), so does the other. The constant is the rate of increase or decrease. In Example 11, the number of pages Sharon reads varies directly with the number of minutes she reads. Sharon’s rate of reading is 1.6 pages per minute.

The quotient 

EXAMPLE 16

If p is directly proportional to q, and if q = 12 when p = 8, then what is the value of p when q = 15?

Solution. Since p and q are directly proportional, the quoteint  is a constant, so  Cross-multiply:

12p = 8 × 15 = 120  p = 10.

In some problems, however, as one quantity increases, the other decreases. These problems cannot be solved by setting up a proportion. Consider Examples 17 and 18, which look similar but must be handled differently.

EXAMPLE 17

A hospital needs 150 pills to treat 6 patients for a week. How many pills does it need to treat 10 patients for a week?

EXAMPLE 18

A hospital has enough pills on hand to treat 10 patients for 14 days. How long will the pills last if there are 35 patients?

Solution 17. Example 16 is a standard rate problem. The more patients there are, the more pills are needed.

The ratio or quotient remains constant:

In Example 18, the situation is different. With more patients, the supply of pills will last for a shorter period of time; if there were fewer patients, the supply would last longer. It is not the ratio that remains constant; it is the product

Solution 18. We are told that the hospital has enough pills to last for 10 × 14 = 140 patient-days:

     140 patient-days = (10 patients) × (14 days).

     140 patient-days = (20 patients) × (7 days).

     140 patient-days = (70 patients) × (2 days).

To solve Example 18, write:

Problems like this one are examples of inverse variation. We say that one variable is inversely proportional to a second variable if their product is a constant. If y is inversely proportional to x, there is a constant k such that xy =k.

Helpful Hint

Be sure you understand the definitions of direct variation and indirect variation.

EXAMPLE 19

If p is inversely proportional to q², and if q = 2 when p = 6, what is the value of p when q = 6?

Solution. Since p and q² are inversely proportional, the product pq²is a constant, so

In Example 18, the number of patients varies inversely with the number of days that the supply of pills lasts. The product, patients × days, is constant. Notice that, as the number of patients increases from 10 to 20 to 70, the number of days the supply of pills lasts decreases, from 14 to 7 to 2.

EXAMPLE 20

If 15 workers can paint a certain number of houses in 24 days, how many days will 40 workers take, working at the same rate, to do the same job?

Solution. Clearly, the more workers there are, the less time will be required. This is an example of inverse variation, so multiply. The job takes:

(15 workers) × (24 days) = 360 worker-days.

Then (40 workers) × (d days) = 360 worker-days.

40d = 360  d = 9.

This job will take 9 days.

Exercises on Ratios and Proportions

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

1. If  of the workers in an office are nonsmokers, what is the ratio of smokers to nonsmokers?

(A) 2:5

(B) 1:2

(C) 3:5

(D) 2:3

(E) 3:2

2. If 80% of the applicants to a program were rejected, what is the ratio of the number accepted to the number rejected?

3. The measures of the three angles in a triangle are in the ratio 1:1:2. Which of the following must be true?

  I. The triangle is isosceles.

 II. The triangle is a right triangle.

III. The triangle is equilateral.

(A) None

(B) I only

(C) II only

(D) I and II only

(E) I and III only

4. What is the ratio of the circumference of a circle to its radius?

5. If a:b = 3:5 and a:c = 5:7, what is the value of b:c?

(A) 3:7

(B) 21:35

(C) 21:25

(D) 25:21

(E) 7:3

6. In the diagram below, b:a = 7:2. What is b – a?

(A)   20

(B)   70

(C) 100

(D) 110

(E) 160

7. If x is a positive number and,  then x =

(A)   3

(B)   4

(C)   6

(D) 12

(E) 36

8. A snail can move i inches in m minutes. At this rate, how many feet can it move in h hours?

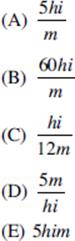
9. Barbra can grade t tests in  hours. At this rate, how many tests can she grade in x hours?

10. If 500 pounds of mush will feed 20 pigs for a week, for how many days will 200 pounds of mush feed 14 pigs?

(A) 4

(B) 5

(C) 6

(D) 7

(E) 8

Grid-in Questions

11. John can read 72 pages per hour. At this rate, how many pages can he read in 72 minutes?

12. If 3a = 2b and 3b = 5c, what is the ratio of a to c?

13. If , what is the value of x?

14. Three associates agreed to split the profit of an investment in the ratio of 2:5:8. If the profit was $3000, what is the difference between the largest share and the smallest?

15. If y is inversely proportional to x, and y = 8 when x = 4, what is the value of y when x = 5?

Answer Key

1. B   2. B   3. D   4. E

5. D   6. C   7. C   8. A

9. B 10. A

Answer Explanations

1. (B).   Of every 3 workers, 2 are nonsmokers, and 1 is a smoker. Then, the ratio of smokers to nonsmokers is 1:2.

2. (B).   If 80% of the applicants were rejected, 20% were accepted, and the ratio of accepted to rejected is 20:80 = 1:4 = .

3. (D).   It is worth remembering that, if the ratio of the measures of the angles of a triangle is 1:1:2, then the angles are 45-45-90 (see Section 9-J). Otherwise, the first step is to write

• Since two of the angles have the same measure, the triangle is isosceles. (I is true.)

• Also, since one of the angles measures 90°, the triangle is a right triangle. (II is true.)

• Statement III, of course, is false.

4. (E). By definition, π is the ratio of the circumference to the diameter of a circle (see Section 12-L), so

5. (D). Since  then .

Alternatively, you could write equivalent ratios with the same value for a:

a:b = 3:5 = 15:25    and    a:c = 5:7 = 15:21.

Then, when a = 15, b = 25 and c = 21.

6. (C). Let b = 7x and a = 2x. Then

7. (C). To solve a proportion, cross-multiply:

8. (A). Set up the proportion, keeping track of units:

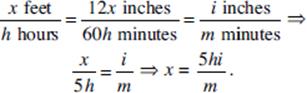
9. (B). Barbra grades at the rate of .

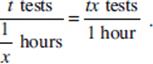
Since she can grade tx tests each hour, in x hours she can grade x(tx) = tx² tests.

10. (A). Since 500 pounds will last for 20 pig-weeks or 140 pig-days, 200 pounds will last for

,

and

11. (86.4) Set up a proportion:

    and cross-multiply: 72 × 72 = 60x  5184 = 60x  x = 86.4.

12.  Multiplying each equation to get the same coefficient of b gives 9a = 6b and 6b = 10c  9a = 10c 

13. (17) Cross-multiplying gives

14. (1200) The shares are 2x, 5x, and 8x, and their sum is 3000:

2x + 5x + 8x = 3000  15x = 3000  x = 200, so 8x – 2x = 6x = 1200.

15.  If y is inversely proportional to x, there is a constant k such that xy = k, so k = (8)(4) = 32. Thus

9-E Averages

The average of a set of n numbers is the sum of those numbers divided by n:

or simply

If you took three math tests so far this year and your grades were 80, 90, and 76, to calculate your average, you would add the three grades and divide by 3:

The technical name for average is “arithmetic mean,” and on the SAT those words always appear in parentheses—for example, “What is the average (arithmetic mean) of 80, 90, and 76?”

Very often on the SAT, you are not asked to find an average; rather, you are given the average of a set of numbers and asked to provide some other information. The key to solving all of sum these problems is to first find the sum of the numbers. Since  multiplying both sides by n yields this equation: sum = nA.

Helpful Hint

On the SAT you can ignore the words “arithmetic mean.” They simply mean “average.”

TACTIC E1

If you know the average, A, of a set of n numbers, multiply A by n to get their sum.

Helpful Hint

Most SAT problems involving averages can be solved using TACTIC 1.

EXAMPLE 1

One day a delivery-truck driver picked up 25 packages whose average (arithmetic mean) weight was 14.2 pounds. What was the total weight, in pounds, of all the packages?

 Solution. Use TACTIC E1: 25 × 14.2 = 355.

NOTE: You do not know how much any individual package weighed or how many packages weighed more or less than 14.2 pounds. All you know is the total weight.

EXAMPLE 2

John took five English tests during the first marking period, and his average (arithmetic mean) was 85. If his average after the first three tests was 83, what was the average of his fourth and fifth tests?

(A) 83

(B) 85

(C) 87

(D) 88

(E) 90

 Solution.
• Use TACTIC E1: On his five tests John earned 5 × 85 = 425 points.

• Use TACTIC E1 again: On the first three tests he earned 3 × 83 = 249 points.

• Subtract: On his last two tests he earned 425 – 249 = 176 points.

• Calculate his average on his last two tests: 

NOTE: You cannot determine John’s grade on even one of the five tests.

Key Fact E1

If all the numbers in a set are the same, then that number is the average.

Key Fact E2

If the numbers in a set are not all the same, then the average must be greater than the smallest number and less than the largest number. Equivalently, at least one of the numbers is less than the average and at least one is greater.

If Mary’s test grades are 85, 85, 85, and 85, her average is 85. If Bob’s test grades are 76, 83, 88, and 88, his average must be greater than 76 and less than 88. What can we conclude if, after taking five tests, Ellen’s average is 90? We know that she earned exactly 5 × 90 = 450 points, and that either she got 90 on every test or at least one grade was less than 90 and at least one was over 90. Here are a few of the thousands of possibilities for Ellen’s grades:

(a) 90, 90, 90, 90, 90
(b) 80, 90, 90, 90, 100 
(c) 83, 84, 87, 97, 99 
(d) 77, 88, 93, 95, 97 
(e) 50, 100, 100, 100, 100

Key Fact E3

Assume that the average of a set of numbers is A. If a number, x, is added to the set and a new average is calculated, then the new average will be less than, equal to, or greater than A, depending on whether x is less than, equal to, or greater than A, respectively.

EXAMPLE 3

Let n be an integer greater than 1, let a = the average (arithmetic mean) of the integers from 1 to n, and let b = the average of the integers from 0 to n. Which of the following could be true?

  I. a = b

 II. a < b

III. a > b

(A) I only

(B) II only

(C) III only

(D) II and III only

(E) I, II, and III

Solution 1. Since a is the average of the integers from 1 to n, a is surely greater than 1. You are told that b is the average of those same n numbers and 0. Since the extra number, 0, is less than a, b must be less than a. Only Statement III (C) is true.

Solution 2. Clearly, the sum of the n + 1 integers from 0 to n is the same as the sum of the n integers from 1 to n. Since that sum is positive, dividing by n + 1 yields a smaller quotient than dividing by n (KEY FACT B4).

If in Example 3 n = 12, then you could calculate each average as follows:

         0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = 78 and  

           1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = 78 and  

Notice that the average of the 13 consecutive integers 0, 1,...,12 is the middle integer, 6, and the average of the 12 consecutive integers 1, 2,...,12 is the average of the two middle integers, 6 and 7. This is a special case of KEY FACT E4.

Key Fact E4

Whenever n numbers form an arithmetic sequence (one in which the difference between any two consecutive terms is the same): (i) if n is odd, the average of the numbers is the middle term in the sequence; and (ii) if nis even, the average of the numbers is the average of the two middle terms.

For example, in the arithmetic sequence 6, 9, 12, 15, 18, the average is the middle number, 12; and in the sequence 10, 20, 30, 40, 50, 60, the average is 35, the average of the two middle numbers—30 and 40.

EXAMPLE 4

On Thursday, 20 of the 25 students in a chemistry class took a test, and their average (arithmetic mean) was 80. On Friday, the other 5 students took the test, and their average (arithmetic mean) was 90. What was the average for the entire class?

(A) 80

(B) 82

(C) 84

(D) 85

(E) 88

 Solution. The class average is calculated by dividing the sum of all 25 test grades by 25.

• The first 20 students earned a total of:	20 × 80 = 1600 points
• The other 5 students earned a total of:	5 × 90 = 450 points
• Add: altogether the class earned:	1600 + 450 = 2050 points
• Calculate the class average:

Notice that the answer to Example 4 is not 85, which is the average of 80 and 90. The averages of 80 and 90 were earned by different numbers of students, and so the two averages must be given different weights in the calculation. For this reason, 82 is called a weighted average.

Helpful Hint

Without doing any calculations, you should immediately realize that, since the grade of 80 is being given more weight than the grade of 90, the average will be closer to 80 than to 90—certainly less than 85.

Key Fact E5

To calculate the weighted average of a set of numbers, multiply each number in the set by the number of times it appears, add all the products, and divide by the total number of numbers in the set.

 The solution to Example 4 should look like this:

Problems involving average speed will be discussed in Section 9-H, but we mention them briefly here because they are closely related to problems on weighted averages.

EXAMPLE 5

For the first 3 hours of her trip, Susan drove at 50 miles per hour. Then, because of construction delays, she drove at only 40 miles per hour for the next 2 hours. What was her average speed, in miles per hour, for the entire trip?

 Solution. This is just a weighted average:

Note that in each of the above fractions the numerator is the total distance traveled and the denominator the total time the trip took. This is always the way to find an average speed. Consider the following slight variation of Example 5.

EXAMPLE 5A

For the first 100 miles of her trip, Susan drove at 50 miles per hour. Then, because of construction delays, she drove at only 40 miles per hour for the next 120 miles. What was her average speed, in miles per hour, for the entire trip?

 Solution. This is not a weighted average. Here you immediately know the total distance: 220 miles. To get the total time, find the time for each portion and add: the first 100 miles took 100 ÷ 50 = 2 hours, and the next 120 miles took 120 ÷ 40 = 3 hours. The average speed was  miles per hour.

Notice that in Example 5, since Susan spent more time traveling at 50 than at 40 miles per hour, her average speed was closer to 50; in Example 5a, however, she spent more time driving at 40 than at 50 miles per hour, so her average speed was closer to 40.

Two other terms associated with averages are median and mode.

• In a set of n numbers arranged in increasing order, the median is the middle number (if n is odd), or the average of the two middle numbers (if n is even).

• In any set of numbers, the mode is the number that appears most often.

EXAMPLE 6

During a 10-day period, Olga received the following number of phone calls each day: 2, 3, 9, 3, 5, 7, 7, 10, 7, 6. What is the average (arithmetic mean) of the median and mode of this set of data?

 Solution. The first step is to write the data in increasing order: 2, 3, 3, 5, 6, 7, 7, 7, 9, 10.

• The median is 6.5, the average of the middle two numbers.

• The mode is 7, the number that appears more often than any other.

• The average of the median and the mode is 

Exercises on Averages

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

  1. Justin’s average (arithmetic mean) on four tests is 80. What grade does he need on his fifth test to raise his average to 84?

(A) 82

(B) 84

(C) 92

(D) 96

(E) 100

  2. Judy’s average (arithmetic mean) on four tests is 80. Assuming she can earn no more than 100 on any test, what is the least she can earn on her fifth test and still have a chance for an 85 average after seven tests?

(A) 60

(B) 70

(C) 75

(D) 80

(E) 85

  3. Adam’s average (arithmetic mean) on four tests is 80. Which of the following CANNOT be the number of tests on which he earned exactly 80 points?

(A) 0

(B) 1

(C) 2

(D) 3

(E) 4

  4. If a + b = 3(c + d), which of the following is the average (arithmetic mean) of a, b, c, and d?

  5. If the average (arithmetic mean) of 5, 6, 7, and w is 8, what is the value of w?

(A)   8

(B) 12

(C) 14

(D) 16

(E) 24

  6. In the diagram above, lines  and m are not parallel. If A represents the average (arithmetic mean) of the measures of all eight angles, which of the following is true?

(A) A = 45°

(B) 45° < A < 90°

(C) A = 90°

(D) 90° < A < 180°

(E) It cannot be determined from the information given.

  7. What is the average (arithmetic mean) of 2¹⁰ and 2²⁰?

(A) 2¹⁵

(B) 2⁵ + 2¹⁰

(C) 2⁹ + 2¹⁹

(D) 2²⁹

(E) 30

  8. Let M be the median, and m the mode, of the following set of numbers: 10, 70, 20, 40, 70, 90. What is the average (arithmetic mean) of M and m?

(A) 50

(B) 55

(C) 60

(D) 62.5

(E) 65

  9. Which of the following is the average (arithmetic mean) of x² – 10, 30 – x², and 6x + 10?

(A) 2x + 10

(B) 2x + 30

(C) 3x + 15

(D) 2x² + 6x + 30

(E) 6x + 10

Grid-in Questions

10. The average (arithmetic mean) weight of the students in the French Club is 150 pounds, and the average weight of the students in the Spanish Club is 130 pounds. If no one is a member of both clubs, if the average weight of all the students is 142 pounds, and if there are 30 members in the French Club, how many members are there in the Spanish Club?

11. If 10a + 10b = 35, what is the average (arithmetic mean) of a and b?

12. What is the average (arithmetic mean) of the measures of the five angles in a pentagon?

Answer Key

1. E   2. C   3. D

4. E   5. C   6. C

7. C   8. D   9. A

Answer Explanations

1. (E). Use TACTIC E1. For Justin’s average on five tests to be 84, he needs a total of 5 × 84 = 420 points. So far, he has earned 4 × 80 = 320 points. Therefore, he needs a grade of 100 points on the fifth test.

2. (C). Use TACTIC E1. So far, Judy has earned 320 points. She can survive a low grade on test 5 if she gets the maximum possible on both the sixth and seventh tests. Assume she gets two 100’s. Then her total for tests 1, 2, 3, 4, 6, and 7 will be 520. For her seven-test average to be 85, she needs a total of 7 × 85 = 595 points. Therefore, she needs at least 595 – 520 = 75 points.

3. (D). Adam could not have earned exactly 80 on three tests. If he did, his average for those three tests would clearly be 80; and since adding the fourth score didn’t change his average, KEY FACT E3 tells us that his fourth score must also be 80. Therefore, it is not possible for him to have earned exactly 80 on each of three tests.
Alternative solution. Could Adam have earned a total of 320 points with:

0 grade of 80?	Easily; for example, 20, 100, 100, 100 or 60, 70, 90, 100.
1 grade of 80?	Lots of ways; 80, 40, 100, 100, for instance.
2 grades of 80?	Yes; 80, 80, 60, 100, for instance.
4 grades of 80?	Sure: 80, 80, 80, 80.
3 grades of 80?	No! If 80 + 80 + 80 + x = 320, then x = 80, as well.

4. (E). Calculate the average:

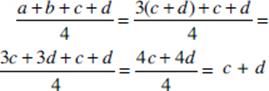
5. (C). Use TACTIC E1. The sum of the four numbers is 4 × 8 = 32. Then

6. (C). a + b + c + d = 360 and w + x + y + z = 360 (see Section 9-I); so the sum of the measures of all eight angles is 360° + 360° = 720°, and their average, A, is 720° ÷ 8 = 90°.

7. (C). The average of 2¹⁰ and 2²⁰ is

(See Section 9-A if you had trouble with the exponents.)

Alternative solution. Use your calculator and estimate: 2¹⁰ is about 1000 and 2²⁰ is about 1,000,000. Their average is about 500,000. None of the wrong choices is even close.

8. (D). Arrange the numbers in increasing order: 10, 20, 40, 70, 70, 90. The median, M, is the average of the middle two numbers:

 the mode, m, is 70, the number that appears most frequently. The average of M and m, therefore, is the average of 55 and 70, which is 62.5.

9. (A). Find the sum of the three expressions, and divide by 3:

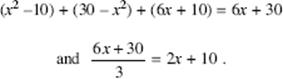
Alternative solution. If you get bogged down in the algebra, use TACTIC 6 from Chapter 8. Choose an easy number for x: 1, for example. Then, the three numbers become –9, 29, and 16, whose average is 12. Only A has a value of 12 when x = 1. This is also an easy way to check your answer, if you use the first solution.

10. (20) Let x = number of students in the Spanish Club, and write the weighted average:

              Cross-multiply:

11.  Since 10a + 10b = 35, dividing both sides of the equation by 10 gives a + b = 3.5. Therefore, the average of a and b is 3.5 ÷ 2 = 1.75 or 

12. (108) The average of the measures of the five angles is the sum of their measures divided by 5. The sum is (5 – 2) × 180 = 3 × 180 = 540 (see Section 9-K), so their average is 540 ÷ 5 = 108.

ALGEBRA

For the SAT you need to know only a small part of the algebra normally taught in high school. Sections 9-F, 9-G, and 9-H review only the albegraic topics that you need for the SAT.

9-F Polynomials

Even though the terms monomial, binomial, trinomial, and polynomial are not used on the SAT, you must be able to work with simple polynomials, and the use of these terms will make it easy to discuss the important concepts.

A monomial is any number or variable or product of numbers and variables. Each of the following is a monomial:

3   –4   x   y   3x   –4xyz   5x³   1.5xy²   a³b⁴

The number that appears in front of the variable or variables in a monomial is called the coefficient. The coefficient of 5x ³ is 5. If there is no number, the coefficient is 1 or –1, because x means 1x and –ab² means –1ab².

On the SAT, you are often asked to evaluate a monomial for specific values of the variables.

EXAMPLE 1

What is the value of –3a² b when a = –4 and b = 0.5?

Solution. Rewrite the expression, replacing the letters a and b by the numbers –4 and 0.5, respectively. Make sure to write each number in parentheses. Then evaluate: –3(–4)2(0.5) = –3(16)(0.5) = –24.

CAUTION: Be sure you follow PEMDAS: handle exponents before the other operations. In Example 1, you cannot multiply –4 by –3, get 12, and then square 12.

A polynomial is a monomial or the sum of two or more monomials. Each monomial that makes up the polynomial is called a term of the polynomial. Each of the following is a polynomial:

The first polynomial in the above list is a monomial; the second, third, fifth, and sixth polynomials are called binomials because each has two terms; the fourth and seventh polynomials are called trinomials because each has three terms. Two terms are called like terms if they have exactly the same variables and exponents; they can differ only in their coefficients: 5a²b and –3a ²b are like terms, whereas a²b and b² a are not.

The polynomial 3x² + 4x + 5x + 2x²+ x – 7 has six terms, but some of them are like terms and can be combined:

3x² + 2x² = 5x² and 4x + 5x + x = 10x.

Therefore, the original polynomial is equivalent to the trinomial 5x² + 10x – 7.

Key Fact F1

The only terms of a polynomial that can be combined are like terms.

Key Fact F2

To add two polynomials, first enclose each one in parentheses and put a plus sign between them; then erase the parentheses and combine like terms.

Helpful Hint

To add, subtract, multiply, and divide polynomials, use the usual laws of arithmetic. To avoid careless errors, write each polynomial in parentheses before performing any arithmetic operations.

EXAMPLE 2

What is the sum of 5x² + 10x – 7 and 3x² – 4x + 2?

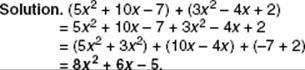
Key Fact F3

To subtract two polynomials, enclose each one in parentheses, change the minus sign between them to a plus sign, and change the sign of every term in the second parentheses. Then use KEY FACT F2 to add them: erase the parentheses and combine like terms.

CAUTION: Make sure you get the order right in a subtraction problem.

EXAMPLE 3

Subtract 3x² – 4x + 2 from 5x² + 10x – 7.

Solution. Be careful. Start with the second polynomial and subtract the first:

EXAMPLE 4

What is the average (arithmetic mean) of 5x² + 10x – 7, 3x² – 4x + 2, and 4x² + 2?

Solution. As in any average problem, add and divide:

(5x² + 10x – 7) + (3x² – 4x + 2) + (4x² + 2) = 12x² + 6x – 3,

and by the distributive law (KEY FACT A22):

Key Fact F4

To multiply monomials, first multiply their coefficients, and then multiply their variables by adding the exponents (see Section 9-A).

EXAMPLE 5

What is the product of 3xy²z³ and –2x²y?

Solution. (3xy²z³)(–2x²y ) = 3(–2)(x)(x²)(y²)(y)(z³) = –6x³y³z³.

All other polynomials are multiplied by using the distributive law.

Key Fact F5

To multiply a monomial by any polynomial, just multiply each term of the polynomial by the monomial.

EXAMPLE 6

What is the product of 2a and 3a² – 6ab + b² ?

On the SAT, the only other polynomials that you may be asked to multiply are two binomials.

Key Fact F6

To multiply two binomials, use the so-called FOIL method, which is really nothing more than the distributive law. Multiply each term in the first parentheses by each term in the second parentheses and simplify by combining terms, if possible.

EXAMPLE 7

What is the value of (x – 2)(x + 3) – (x – 4)(x + 5)?

Solution. First, multiply both pairs of binomials:

(x – 2)(x + 3) = x² + 3x – 2x – 6 = x² + x – 6

(x – 4)(x + 5) = x² + 5x – 4x – 20 = x² + x – 20

Now, subtract: (x² + x – 6) – (x² + x – 20) = x² + x – 6 – x² – x + 20 = 14.

Key Fact F7

The three most important binomial products on the SAT are these:

• (x – y)(x + y) = x² + xy – yx – y² = x² – y²

• (x – y)² = (x – y)(x – y) = x² – xy – yx + y² = x² – 2xy + y²

• (x + y)² = (x + y)(x + y) = x² + xy + yx + y² = x² + 2xy + y²

Helpful Hint

If you memorize the products in KEY FACT F7, you won’t have to multiply the binomials out each time you need them.

EXAMPLE 8

If a – b = 17.5 and a + b = 10, what is the value of a² – b²?

Solution. Section 9-G reviews the methods used to solve such a pair of equations; but even if you know how to solve them, you should not do so here. You don’t need to know the values of a and b to answer this question. The moment you see a² – b², you should think (a – b)(a + b). Then:

a² – b² = (a – b)(a + b) = (17.5)(10) = 175.

EXAMPLE 9

If x² + y² = 36 and (x + y)² = 64, what is the value of xy?

Solution. Here, 64 = (x + y)² = x² + 2xy + y² = x² + y² + 2xy = 36 + 2xy. Therefore:

2xy = 64 – 36 = 28  xy = 14.

On the SAT, the only division of polynomials you will have to do is to divide a polynomial by a monomial. You will not have to do long division of polynomials.

Key Fact F8

To divide a polynomial by a monomial, use the distributive law. Then simplify each term by reducing the fraction formed by the coefficients to lowest terms and applying the laws of exponents.

EXAMPLE 10

What is the quotient when 32a²b + 12ab³c is divided by 8ab?

Solution. By the distributive law,

Now reduce each fraction: 

On the SAT, the most important way to use the three formulas in KEY FACT F7 is to recognize them in reverse. In other words, whenever you see x² – y², you should realize that it can be rewritten as (x –y )(x + y). This process, which is the reverse of multiplication, is called factoring.

EXAMPLE 11

If x² – y² = 14 and x – y = 7, what is the value of x + y?

Solution. Since x ² – y² = (x – y)(x + y), you have

14 = 7(x + y)  x + y = 2.

Note that you could solve for x and y (x = 4.5, y = –2.5) and then add; but you shouldn’t because this method takes much more time.

To factor a polynomial, you must find other polynomials whose product is the original polynomial. For example, since 2x(3x – 5) = 6x ² – 10x, then 2x and 3x – 5 are each factors of 6x ² – 10x; and since (a –b)(a + b) = a² – b², then (a –b) and (a + b) are factors of a² – b². On the SAT, you will have to do almost no factoring. Occasionally, an SAT will have a question which requires you to solve a very simple quadratic equation such as x² – x – 6 = 0. Often you can solve it by inspection since the roots will be two small integers. At worst you will have to factor:

x² – x – 6 = 0  (x – 3)(x + 2) = 0  x – 3 = 0 or x + 2 = 0  x = 3 or x = –2.

A typical SAT may also have one question that requires you to simplify an algebraic expression. In that case, you will probably have to do some simple factoring.

Key Fact F9

To factor a polynomial, the first step is always to use the distributive property to remove the greatest common factor of all the terms.

For example:

6xy + 8yz = 2y(3x + 4z)     and     x³ + x² + x = x(x² + x + 1)

Key Fact F10

To factor a trinomial use trial and error to find the binomials whose product is the given trinomial.

For example:

x² + 4x + 4 = (x + 2)(x + 2) (see KEY FACT F7).

x² – 3x – 10 = (x – 5)(x + 2).

2x² + 18x + 16 = 2(x² + 9x + 8) = 2(x + 8)(x + 1).

EXAMPLE 12

Which of the following is equivalent to 

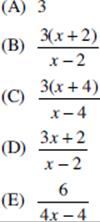
Solution.

In Example 12, when x = 3, the value of 

Only choice B is 15 when 

Note that this method does not depend on the choice of x. You can verify, for example, that, if x = 5, the original expression and the correct answer are both equal to 7.

Although the coefficient of any term in a polynomial can be a fraction, such as  the variable itself cannot be in the denominator. An expression such as,  which has a variable 2 in the denominator, is called an algebraic fraction. Fortunately, you should have no trouble with algebraic fractions since they are handled just like regular fractions. The rules that you reviewed in Section 9-B for adding, subtracting, multiplying, and dividing fractions apply also to algebraic fractions.

Helpful Hint

If you ever get stuck trying to simplify an algebraic expression, just plug in a number and test the answers.

EXAMPLE 13

What is the sum of the reciprocals of x² and y²?

Solution. To add,  you need a common denominator, which is x²y².

Multiply the numerator and denominator of  by y² and the numerator and denominator of 

Exercises on Polynomials

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

1. If a² – b² = 21 and a² + b² = 29, which of the following could be the value of ab?

  I. –10

 II. 

III. 10

(A) I only

(B) II only

(C) III only

(D) I and III only

(E) II and III only

2. What is the average (arithmetic mean) of x² + 2x – 3, 3x² – 2x – 3, and 30 – 4x²?

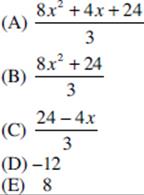
3. If a² + b² = 4 and (a – b)² = 2, what is the value of ab?

(A)1

(B) 

(C) 2

(D) 3

(E) 4

4. If  and ab = c, what is the average (arithmetic mean) of a and b?

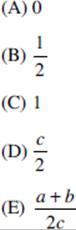
5. If  and  which of the following is equivalent to 

Grid-in Questions

6. What is the value of  when a =17.9 and b = 19.7?

7. If x² – y² = 28 and x – y = 8, what is the average (arithmetic mean) of x and y?

8. What is the value of (2x + 3)(x + 6) – (2x – 5)(x + 10)?

9. What is the value of x² + 12x + 36 when x = 64?

10. If   what is the value of 

Answer Key

1. D 2. E 3. A 4. B 5. B

Answer Explanations

1. (D).   Add the two equations:

2a² = 50  a² = 25  b² = 4.

Then, a = 5 or –5 and b = 2 or –2. The only possibilities for the product ab are –10 and 10. (Only I and III are true.)

2. (E).   To find the average, take the sum of the three polynomials and then divide by 3. The sum is (x² + 2x – 3) + (3x² – 2x – 3) + (30 – 4x²) = 24, and 24 ÷ 3 = 8.

3. (A).   Start by squaring a – b: (a – b)² = a² – 2ab + b². Then

                    2 = 4 – 2ab  2ab = 2  ab = 1.

4. (B).   

5. (B).   

6. (37.6) 

7. (1.75)  Since x² − y² = (x − y)(x + y), we have:

8. (68)   First, multiply out both pairs of binomials:

                    (2x + 3)(x + 6) = 2x² + 15x + 18
and        (2x – 5)(x + 10) = 2x² + 15x – 50.
Now subtract:
               (2x² + 15x + 18) – (2x² + 15x – 50) = 18 – (–50) = 68.

Alternative solution. Note that, since this is a grid-in question, the answer must be a (positive) number. All of the x’s must cancel out. Therefore, the answer will be the same no matter what x is, so pick a simple value for x. If x = 0: (3)(6) – (–5)(10) = 18 – (–50) = 68; if x = 4: (11)(10) – (3)(14) = 110 – 42 = 68.

9. (4900)   Of course, you can do this problem on your calculator; but you can do it quicker if you recognize that x² + 12x + 36 = (x + 6)². The value is (64 + 6)² = 702 = 4900.

10. (98) 

9-G Solving Equations and Inequalities

The most important thing to remember when solving an equation is that you can manipulate the equation in any way, as long as you do the same thing to both sides. For example, you may always add the same number to each side, subtract the same number from each side, multiply or divide each side by the same number (except 0), square each side, take the square root of each side (if the quantities are positive), or take the reciprocal of each side. These comments apply to inequalities, as well, but here you must be very careful because some procedures, such as multiplying or dividing by a negative number and taking reciprocals, reverse inequalities (see KEY FACT A25).

Equations and inequalities that have only one variable and no exponents can be solved using the simple six-step method outlined in the solution of Example 1.

EXAMPLE 1

If  what is the value of x?

Solution. Follow the steps outlined in the following table.

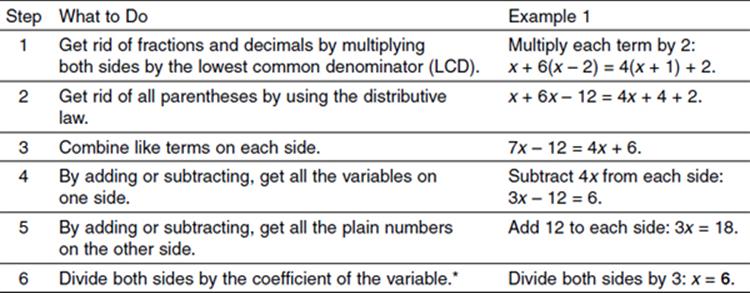
*If you start with an inequality and in Step 6 you divide by a negative number, remember to reverse the inequality (see KEY FACT A25).

Example 1 is actually much harder than any equation on the SAT, because it requires all six steps. On the SAT that never happens. Think of the six steps as a list of questions that must be answered. Ask whether each step is necessary. If it is, do it; if it isn’t, move on to the next one.

Let’s look at Example 2, which does not require all six steps.

EXAMPLE 2

For what real number n is it true that 3(n – 20) = n?

(A) –10

(B)     0

(C)   10

(D)   20

(E)   30

Solution. Do each of the six steps necessary.

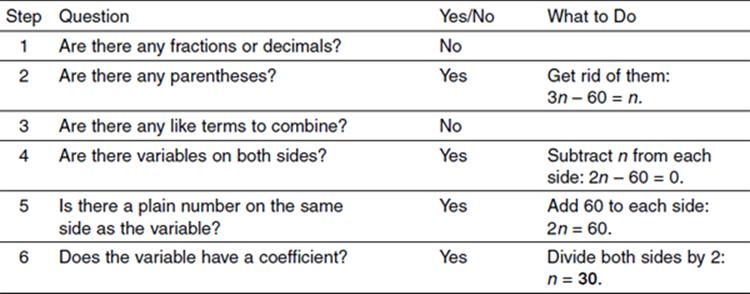
TACTIC G1

Memorize the six steps in order, and use this method whenever you have to solve this type of equation or inequality.

EXAMPLE 3

Three brothers divided a prize as follows. The oldest received , the middle brother received  and the youngest received the remaining $120. What was the value, in dollars, of the prize?

Solution. If x represents the value of the prize, then

Solve this equation using the six-step method.

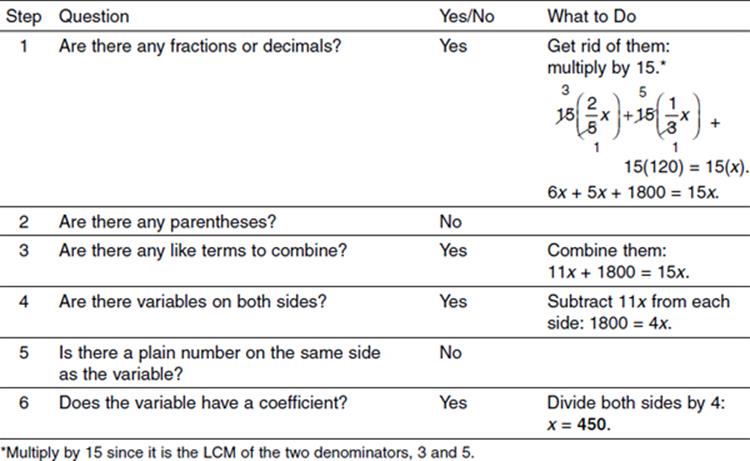
Sometimes on the SAT, you are given an equation with several variables and asked to solve for one of them in terms of the others.

TACTIC G2

When you have to solve for one variable in terms of the others, treat all of the others as if they were numbers, and apply the six-step method.

EXAMPLE 4

If a = 3b – c, what is the value of b in terms of a and c?

Solution. To solve for b, treat a and c as numbers and use the six-step method with b as the variable.

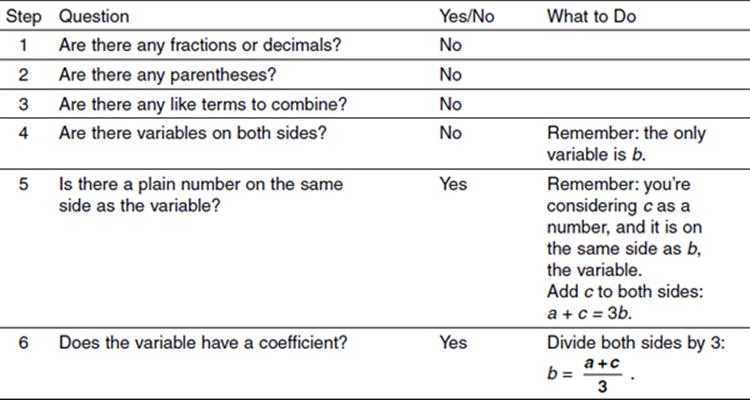
Sometimes when solving equations, you may see a shortcut. For example, to solve 7(w – 3) = 42, you can save time if you start by dividing both sides by 7, getting w – 3 = 6, rather than using the distributive law to eliminate the parentheses. Similarly, if you have to solve a proportion such as  it is easier to cross-multiply, getting 5x = 21, than to multiply both sides by 35 to get rid of the fractions (although that’s exactly what cross-multiplying accomplishes). Other shortcuts will be illustrated in the problems at the end of the section. If you spot such a shortcut, use it; but if you don’t, be assured that the six-step method always works.

EXAMPLE 5

If x – 4 = 11, what is the value of x – 8?

(A) –15

(B) –7

(C) –1

(D)   7

(E)   15

Solution. Going immediately to Step 5, add 4 to each side of the equation: x = 15. But this is not the answer. You need the value, not of x, but of x – 8: 15 – 8 = 7 (D).

Helpful Hint

In applying the six-step method, you shouldn’t actually write out the table, as was done in Examples 1–4, since it would be too time-consuming. Instead, use the method as a guideline and mentally go through each step, doing whichever ones are required.

As in Example 5, on the SAT you are often asked to solve for something other than the simple variable. In Example 5, you could have been asked for the value of x², x + 4, (x – 4)², and so on.

TACTIC G3

As you read each question on the SAT, circle in your test booklet what you are looking for. Then you will always be sure to answer the question that is asked.

Occasionally on the SAT, you will have to solve an equation such as 3 – 1 = 5, which involves a radical. Proceed normally, treating the radical as the variable and using whichever of the six steps are necessary until you have a radical equal to a number. Then raise each side to the same power. For example, if the radical is a square root, square both sides; if the radical is a cube root, cube both sides.

EXAMPLE 6

If 3 – 1 = 5, then x =

Solution.

EXAMPLE 7

If  then x =

Solution.

EXAMPLE 8

If  then x =

Solution.

Helpful Hint

Very often, solving the given equation is not the quickest way to answer a question.

EXAMPLE 9

If 2x – 5 = 98, what is the value of 2x + 5?

Solution. First, circle what you are asked for (the value of 2x + 5), and then look at the question carefully. The best approach is to observe that 2x + 5 is 10 more than 2x – 5, so the answer is 108 (10 more than 98). Next best would be to do only one step of the six-step method, and add 5 to both sides: 2x = 103. Now, again add 5 to both sides: 2x + 5 = 103 + 5 = 108. The worst method would be to divide 2x = 103 by 2, get x = 51.5, and then use that value to calculate 2x + 5.

EXAMPLE 10

If w is an integer, and the average (arithmetic mean) of 3, 4, and w is less than 10, what is the greatest possible value of w?

Solution.

• Set up the inequality: 

• Get rid of fractions: 3 + 4 + w < 30.

• Combine like terms: 7 + w < 30.

• Subtract 7 from both sides: w < 23.

Since w is an integer, the most it can be is 22.

Consider the following variation of Example 10.

EXAMPLE 10A

Assume that this is a grid-in question.

If the average (arithmetic mean) of 3, 4, and w is less than 10, what is the greatest possible value of w that can be entered in the grid?

Solution. Just as in Example 10, you get w < 23. The largest number less than 23 that can be entered in a grid is 22.9.

The six-step method works also when there are variables in denominators.

EXAMPLE 11

For what value of x is 

Solution. Multiply each side by the LCD, 5x:

Now solve normally:

20 + 3x = 50  3x = 30  x = 10.

EXAMPLE 12

If x is positive, and y = 5x² + 3, which of the following is an expression for x in terms of y?

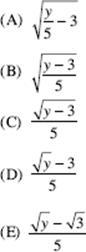
Solution. The six-step method works only when there are no exponents. So, treat x² as a single variable, and use the method as far as you can:

Now take the square root of each side: 

CAUTION: Doing the same thing to each side of an equation does not mean doing the same thing to each term of the equation. Study Examples 13 and 14 carefully.

EXAMPLE 13

If  what is a in terms of b and c?

Note: You cannot just take the reciprocal of each term; the answer is not a = b + c. Here are two solutions.

Solution 1. First add the fractions on the right-hand side:

Now, take the reciprocal of each side: 

Solution 2. Use the six-step method. Multiply each term by abc, the LCD:

EXAMPLE 14

If a > 0 and a² + b² = c², what is a in terms of b and c?

Note: You cannot take the square root of each term and write a + b = c.

Solution. a² + b² = c² a² = c² – b². Now, take the square root of each side:

EXAMPLE 15

If a = b(c + d), what is d in terms of a, b, and c?

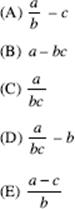
Solution. Use the six-step method:

Now what? This answer isn’t one of the choices. It is, however, equivalent to one of the choices. Use the distributive law to divide a by b and bc by b:

There are a few other types of equations that you may need to solve on the SAT. Fortunately, they are quite easy. You probably will not have to solve a quadratic equation, one in which the variable is raised to the second power. If you do, however, you will not need the quadratic formula, and you will probably not have to factor. Here are two examples.

Helpful Hint

On a multiple-choice question, if your answer is not among the five choices, check to see whether it is equivalentto one of the choices.

EXAMPLE 16

If x is a positive number and x² + 4 = 125, what is the value of x?

Solution. When there is an x²-term, but no x-term, just take the square root:

If the equation had been x² + 9 = 125, the solution would have been  Since 116 = 4 × 29, this can be reduced to .

 Calculator Shortcut

If you can easily simplify a square root, that’s great; but on the SAT, you never have to. The answers to grid-in problems don’t involve square roots, and if the answer to a multiple-choice question turns out to be  you can use your calculator to see which of the five choices is equal to 10.77.

EXAMPLE 17

What is the largest value of x that satisfies the equation 2x² – 3x = 0?

Solution. When an equation has an x²-term and an x-term but no constant term, solve by factoring out the x and using the fact that, if the product of two numbers is 0, one of them must be 0 (KEY FACT A3):

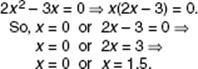
The largest value is 1.5.

In another type of equation that occasionally appears on the SAT, the variable is in the exponent. Equations of this type can often be solved by inspection.

EXAMPLE 18

If  what is the value of 

Solution. How many 2’s do you have to multiply together to get 32? If you don’t know that the answer is 5, just multiply and keep track. Count the 2’s on your fingers as you say to yourself, “2 times 2 is 4, times 2 is 8, times 2 is 16, times 2 is 32.” Then

Therefore, 

Occasionally, both sides of an equation have variables in the exponents. In that case, it is necessary to write both exponentials with the same base.

EXAMPLE 19

If 4^w+3 = 8^w–1, what is the value of w?

Solution. Since it is necessary to have the same base on each side of the equation, write 4 = 2² and 8 = 2³. Then

4^w+3 = (2²)^w+3 = 2^2(w+3) = 2^2w+6

and

8^w–1 = (2³)^w–1 = 2^3(w–1) = 2^3w–3.

Therefore, 2^2w+6 = 2^3w–3  2w + 6 = 3w – 3  w = 9.

Systems of Linear Equations

The equations x + y = 10 and x – y = 2 each have lots of solutions (infinitely many, in fact). Some of them are given in the following tables.

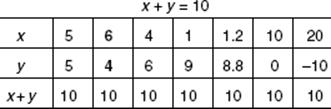
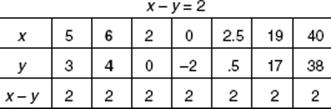
However, only one pair of numbers, x = 6 and y = 4, satisfies both equations simultaneously: 6 + 4 = 10 and 6 – 4 = 2. These numbers, then, are the only solution of the system of

equations 

A system of equations is a set of two or more equations involving two or more variables. To solve such a system, you must find, for all of the variables, values that will make each equation true. In an algebra course you learn several ways to solve systems of equations. On the SAT, the most useful way is to add or subtract (usually add) the equations. Examples 20 and 21 demonstrate this method, and Example 22 shows one other way to handle some systems of equations.

TACTIC G4

To solve a system of equations, add or subtract them. If there are more than two equations, add them.

EXAMPLE 20

If the sum of two numbers is 10 and their difference is 2, what is their product?

Solution. Letting x and y represent the two numbers, write two equations and then add them:

Replacing x by 6 in x + y = 10 yields y = 4. The product of the two numbers is 24.

EXAMPLE 21

If 3a + 5b = 10 and 5a + 3b = 30, what is the average (arithmetic mean) of a and b?

(A) 2.5

(B) 4

(C) 5

(D) 20

(E) It cannot be determined from the information given.

Note: It is not only unnecessary but also foolish to first solve for a and b (a = 7.5 and b = –2.5).

Helpful Hint

On the SAT, most problems involving systems of equations do not require you to solve the systems. These problems usually ask for something other than the value of each variable. Read the questions very carefully, circle what you need, and do not do more than is required.

For additional examples of the proper use of TACTIC G4, see the examples following TACTIC 17 in Chapter 8.

Occasionally on the SAT, it is as easy, or easier, to solve a system of equations by substitution.

TACTIC G5

If one of the equations in a system of equations consists of a single variable equal to some expression, substitute that expression for the variable in the other equation.

EXAMPLE 22

If x + y = 10 and y = x – 2, what is the value of xy?

Solution. This is essentially the same problem as Example 20. However, since here the second equation states that a single variable (y) is equal to some expression (x – 2), substitution is a better method than adding. Replace y by x – 2 in the first equation: x + y = 10 becomes x + (x – 2) = 10. Then

2x – 2 = 10  2x = 12  x = 6.

To find the value of y, replace x by 6 in either of the original equations:

6 + y = 10  y = 4 or y = 6 – 2 = 4.

Finally, xy = (6)(4) = 24.

Exercises on Solving Equations and Inequalities

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

  1. If 4x + 12 = 36, what is the value of x + 3?

(A) 3

(B) 6

(C) 9

(D) 12

(E) 18

  2. If 4x + 13 = 7 – 2x, what is the value of x?

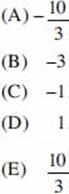
  3. If ax – b = c – dx, what is the value of x in terms of a, b, c, and d?

  4. If , what is the value of x?

(A)   3

(B) 18

(C) 27

(D) 54

(E) 72

  5. If  what is the value of x?

  6. If 32^a+b = 16^a+2b, then a =

(A) b

(B) 2b

(C) 3b

(D) b + 2

(E) b – 2

  7. If the average (arithmetic mean) of 3a and 4b is less than 50, and a is twice b, what is the largest integer value of a?

(A) 9

(B) 10

(C) 11

(D) 19

(E) 20

  8. If  then a =

  9. If x = 3a + 7 and y = 9a², what is y in terms of x?

(A) (x – 7)²

(B) 3(x – 7)²

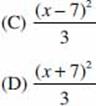
(E) (x + 7)²

10. Which of the following is a solution of 

(A) –2

(B)   1

(C) 

(D)   2

(E) The equation has no solution.

Grid-in Questions

11. If x – 4 = 9, what is the value of x² – 4?

12. If 7x + 10 = 44, what is the value of 7x – 10?

13. If 3x – 4 = 9, what is the value of (3x – 4)²?

14. If  what is one possible value of x?

15. If x² + 3 < 4 and 2x² + 3 > 4, what is one possible value of x?

Answer Key

1. C   2. C   3. A

4. D   5. A   6. C

7. D   8. C   9. A 10. A

Answer Explanations

1.  C.     The easiest method is to recognize that x + 3 is  of 4x + 12, and, therefore, equals  of 36, which is 9. If you don’t see that, solve normally:

4x + 12 = 36  4x = 24  x = 6  x + 3 = 9.

2.  C.     Add 2x to each side: 6x + 13 = 7. Subtract 13 from each side: 6x = –6. Divide by 6: x = –1.

3.  A.     Treat a, b, c, and d as constants, and use the six-step method to solve for x:

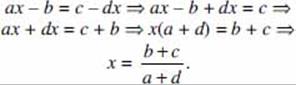
4.  D.     Multiply both sides by 18, the LCD:

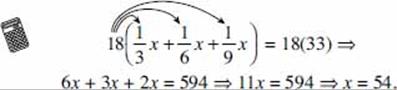
Mentally, it’s easier not to multiply 18 × 33; leave it in that form and divide by 11:

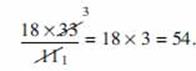 Since you have a

 calculator, however, you might as well use it.

5.  A.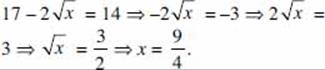     

6.  C.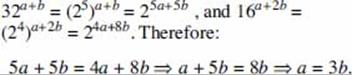     

7.  D.     Since a = 2b, then 2a = 4b. Therefore, the average of 3a and 4b is the average of 3a and 2a, which is 2.5a. Therefore, 2.5a < 50  a < 20, so the largest integer value of a is 19.

8.  C.     Take the reciprocal of each side:

9.  A.     If x = 3a + 7, then x – 7 = 3a and  Therefore

10. (A).   

The equation has two solutions, 0 and –2, but 0 is not a choice. The answer is –2.

11. (165)   x – 4 = 9  x = 13  x² = 169, and so x² – 4 = 165.

12. (24)   Subtracting 20 from each side of 7x + 10 = 44 gives 7x – 10 = 24. If you don’t see that, subtract 10 from each side, getting 7x = 34. Then subtract 10 to get 7x – 10 = 24. The worst alternative is to divide both sides of 7x = 34 by 7 to get x =  then you have to multiply by 7 to get back to 34, and then subtract 10.

13. (81)   Be alert. Since you are given the value of 3x – 4 and want the value of (3x – 4)², just square both sides: 9² = 81. If you don’t see that, you’ll waste time solving 3x – 4 = 9 x  only to use that value to calculate that 3x – 4 is equal to 9, which you aready knew.

14. (2)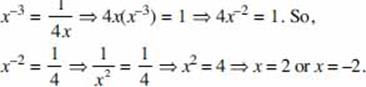   

Since –2 cannot be entered in a grid, the only acceptable solution is 2.

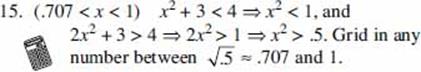
9-H Word Problems

A typical SAT has several word problems, covering almost every math topic for which you are responsible. In this chapter you have already seen word problems on consecutive integers in Section 9-A, fractions and percents in Sections 9-B and 9-C, ratios and proportions in Section 9-D, and averages in Section 9-E. Later in this chapter you will see word problems involving circles, triangles, and other geometric figures. A few of these problems can be solved just with arithmetic, but most of them require basic algebra.

To solve word problems algebraically, you must treat algebra as a foreign language and learn to translate “word for word” from English into algebra, just as you would from English into French or Spanish or any other foreign language. When translating into algebra, you use some letter (often x) to represent the unknown quantity you are trying to determine. It is this translation process that causes difficulty for some students. Once the translation is completed, solving is easy using the techniques already reviewed.

Consider the pairs of typical SAT questions in Examples 1 and 2. The first ones in each pair (1a and 2a) would be considered easy, whereas the second ones (1b and 2b) would be considered harder.

EXAMPLE 1A

What is 4% of 4% of 40,000?

EXAMPLE 1B

In a lottery, 4% of the tickets printed can be redeemed for prizes, and 4% of those tickets have values in excess of $100. If the state prints 40,000 tickets, how many of them can be redeemed for more than $100?

EXAMPLE 2A

If x + 7 = 2(x – 8), what is the value of x?

EXAMPLE 2B

In 7 years Erin will be twice as old as she was 8 years ago. How old is Erin now?

Once you translate the words into arithmetic expressions or algebraic equations, Examples 1a and 1b and 2a and 2b are clearly identical. The problem that many students have is doing the translation. It really isn’t very difficult, and you’ll learn how. First, though, look over the following English-to-algebra “dictionary.”

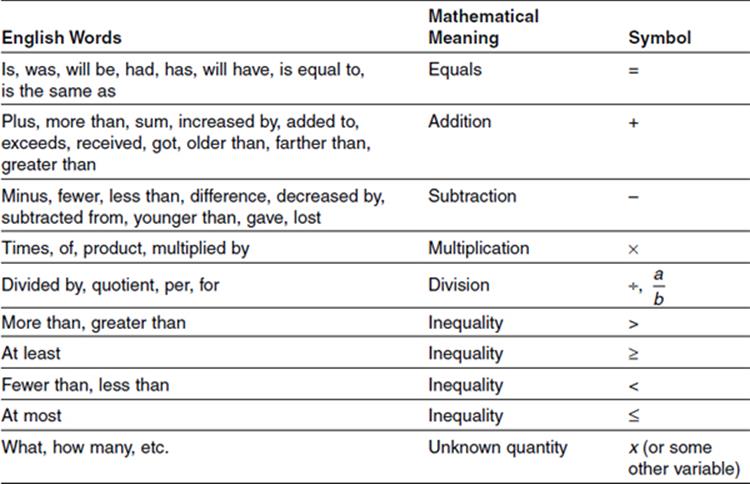
Let’s use this “dictionary” to translate some phrases and sentences.

In translating a statement, you first must decide what quantity the variable will represent. Often, this is obvious. Other times there is more than one possibility.

Let’s translate and solve the two examples at the beginning of this section, and then look at a few new ones.

EXAMPLE 1B

In a lottery, 4% of the tickets printed can be redeemed for prizes, and 4% of those tickets have values in excess of $100. If the state prints 40,000 tickets, how many of them can be redeemed for more than $100?

 Solution. Let x be the number of tickets worth more than $100. Then

x = 4% of 4% of 40,000 = 0.04 × 0.04 × 40,000 = 64,

which is also the solution to Example 1a.

EXAMPLE 2B

In 7 years Erin will be twice as old as she was 8 years ago. How old is Erin now?

Solution. Let x be Erin’s age now; 8 years ago she was x – 8 and 7 years from now she will be x + 7. Then,

x + 7 = 2(x – 8),

and

x + 7 = 2(x – 8) x + 7 = 2x – 16  7 = x – 16 x = 23, which is also the solution to Example 2a.

EXAMPLE 3

The product of 2 and 8 more than a certain number is 10 times that number. What is the number?

Solution. Let x represent the unknown number. Then

2(8 + x) = 10x,

and

2(8 + x) = 10x  16 + 2x = 10x  8x = 16  x = 2.

EXAMPLE 4

If the sum of three consecutive integers is 20 more than the middle integer, what is the smallest of the three?

Solution. Let n represent the smallest of the three integers. Then

n + (n + 1) + (n + 2) = 20 + (n + 1),

and

n + n + 1 + n + 2 = 20 + n + 1  3n + 3 = 21 + n  2n + 3 = 21  2n = 18  n = 9.

(The integers are 9, 10, and 11.)

Most algebraic word problems on the SAT are not very difficult. If, after studying this section, you still get stuck on a question, don’t despair. Use the tactics that you learned in Chapter 8. In each of Examples 3 and 4, if you had been given choices, you could have backsolved; and if the questions had been grid-ins, you could have used trial and error (effectively, backsolving by making up your own choices). Here’s how.

 Alternative Solution to Example 3. Pick a starting number and test (using your calculator, if necessary).

Try 10: 8 + 10 = 18 and 2 × 18 = 36, but 10 × 10 = 100, which is much too big.

Try 5: 8 + 5 = 13 and 2 × 13 = 26, but 10 × 5 = 50, which is still too big.

Try 2: 8 + 2 = 10 and 2 × 10 = 20, and 10 × 2 = 20. That’s it.

Alternative Solution to Example 4. You need three consecutive integers whose sum is 20 more than the middle one. Obviously, 1, 2, 3 and 5, 6, 7 are too small; neither one even adds up to 20.

Try 10, 11, 12: 10 + 11 + 12 = 33, which is 22 more than 11—a bit too much.

Try 9, 10, 11: 9 + 10 + 11 = 30, which is 20 more than 10.

Of course, if you can do the algebra, that’s usually the best way, to handle these problems. On grid-ins you might have to backsolve with several numbers before zooming in on the correct answer; also, if the correct answer was a fraction, such as  you might never find it. In the rest of this section, the proper ways to set up and solve various word problems are stressed.

Helpful Hint

In all word problems on the SAT, remember to circle what you’re looking for. Don’t answer the wrong question!

Age Problems

In problems involving averages, remember that “years ago” means you need to subtract, and “years from now” means you need to add.

EXAMPLE 5

In 1980, Judy was 3 times as old as Adam, but in 1984 she was only twice as old as he was. How old was Adam in 1990?

(A) 4

(B) 8

(C) 12

(D) 14

(E) 16

Solution. Let x be Adam’s age in 1980, and fill in the table below.

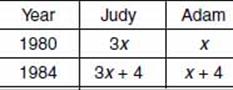
Now translate: Judy’s age in 1984 was twice Adam’s age in 1984:

Adam was 4 in 1980. However, 4 is not the answer to this question. Did you remember to circle what you’re looking for? The question could have asked for Adam’s age in 1980 (choice A) or 1984 (choice B) or Judy’s age in any year whatsoever (choice C is 1980, and choice E is 1984); but it didn’t. It asked for Adam’s age in 1990. Since he was 4 in 1980, then 10 years later, in 1990, he was 14 (D).

Helpful Hint

It is often very useful to organize the data from a word problem in a table.

Distance Problems

All distance problems involve one of three variations of the same formula:

These are usually abbreviated as 

EXAMPLE 6

How much longer, in seconds, is required to drive 1 mile at 40 miles per hour than at 60 miles per hour?

Solution. The time to drive 1 mile at 40 miles per hour is given by

The time to drive 1 mile at 60 miles per hour is given by

The difference is  minute = 30 seconds.

Note that this solution used the time formula given but required only arithmetic, not algebra.

Example 7 requires an algebraic solution.

EXAMPLE 7

Mark drove to a meeting at 60 miles per hour. Returning over the same route, he encountered heavy traffic, and was able to drive at only 40 miles per hour. If the return trip took 1 hour longer, how many miles did he drive each way?

(A)     2

(B)     3

(C)     5

(D) 120

(E) 240

Solution. Let x represent the number of hours Mark took to go, and make a table.

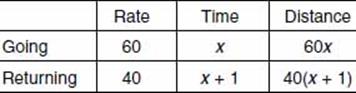
Since Mark drove the same distance going and returning:

60x = 40(x + 1)  60x = 40x + 40  20x = 40  x = 2.

Now be sure to answer the correct question. Choices A, B, and C are the times, in hours, for going, returning, and the round trip; choices D and E are the distances each way and round-trip. You could have been asked for any of the five. If you circled what you’re looking for, you won’t make a careless mistake. Mark drove 120 miles each way, and so the correct answer is D.

The d in the formula d = rt stands for distance, but it could represent any type of work that is performed at a certain rate, r, for a certain amount of time, t. Example 7 need not be about distance. Instead of driving 120 miles at 60 miles per hour for 2 hours, Mark could have read 120 pages at a rate of 60 pages per hour for 2 hours, or planted 120 flowers at the rate of 60 flowers per hour for 2 hours, or typed 120 words at a rate of 60 words per minute for 2 minutes.

This section concludes with a miscellaneous collection of word problems of the type that you may find on the SAT. Some of them are similar to problems already discussed in preceding sections.

EXAMPLE 8

At 8:00 P.M., the hostess of the party remarked that only  of her guests had arrived so far, but that, as soon as 10 more showed up,  of the guests would be there. How many people were invited?

Solution. Let x represent the number of people invited. First, translate the first sentence of the problem into algebra:  Then, use the six-step method of Section 9-G to solve the equation.

Multiply each term by 12: 3x + 120 = 4x.

Subtract 3x from each side: x = 120.

EXAMPLE 9

In a family of three, the father weighed 5 times as much as the child, and the mother weighed  as much as the father. If the three of them weighed a total of 390 pounds, how much did the mother weigh?

In this problem it is easier to let x represent the weight of the child, and 5x the weight of the father, than to let x represent the weight of the father, and  the weight of the child. The worst choice would be to let x represent the weight of the mother; in that case, since the mother’s weight is  that of the father’s, his weight would be  of hers.

Solution. Let x = weight of the child; then 5x = weight of the father, and (5x) = weight of the mother. Since their combined weight is 390:

 Multiply by 4 to get rid of the fraction:

4x + 20x + 15x = 1560.

Combine like terms and then divide:

39x = 1560  x = 40.

The child weighed 40 pounds, the father weighed 5 × 40 = 200 pounds, and the mother weighed.(200) = 150 pounds.

Helpful Hint

You often have a choice as to what you will let the variable represent. Don’t necessarily have it represent what you’re looking for; rather, choose what will make the problem easiest to solve.

EXAMPLE 10

A teacher wrote three consecutive odd integers on the board. She then multiplied the first by 2, the second by 3, and the third by 4. Finally, she added all six numbers and got a sum of 400. What was the smallest number she wrote?

Solution. Let n be the first odd integer she wrote. Since the difference between any two consecutive odd integers is 2 (3, 5, 7, 9, etc.), the next consecutive odd integer is n + 2 and the third is n + 4. The required equation is

n + (n + 2) + (n + 4) + 2n + 3(n + 2) + 4(n + 4) = 400.

 Simplifying gives

Exercises on Word Problems

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

  1. In the afternoon, Judy read 100 pages at the rate of 60 pages per hour; in the evening, when she was tired, she read another 100 pages at the rate of 40 pages per hour. In pages per hour, what was her average rate of reading for the day?

(A) 45

(B) 48

(C) 50

(D) 52

(E) 55

  2. If the sum of five consecutive integers is S, what is the largest of those integers in terms of S?

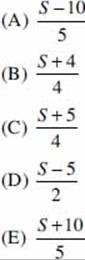
  3. A jar contains only red, white, and blue marbles. The number of red marbles is  the number of white ones, and the number of white ones is  the number of blue ones. If there are 470 marbles in all, how many of them are blue?

(A) 120

(B) 135

(C) 150

(D) 184

(E) 200

  4. As a fund-raiser, the Key Club was selling two types of candy: lollipops at 40 cents each and chocolate bars at 75 cents each. On Monday, the members sold 150 candies and raised 74 dollars. How many lollipops did they sell?

(A)   75

(B)   90

(C)   96

(D) 110

(E) 120

  5. On a certain project the only grades awarded were 75 and 100. If 85 students completed the project and the average of their grades was 85, how many earned 100?

(A) 34

(B) 40

(C) 45

(D) 51

(E) 60

  6. Aaron has 3 times as much money as Josh. If Aaron gives Josh $50, Josh will then have 3 times as much money as Aaron. How much money do the two of them have together?

(A) $ 75

(B) $100

(C) $125

(D) $150

(E) $200

  7. If  years ago Jason was 12, and  years from now he will be 2x years old, how old will he be 3x years from now?

(A) 18

(B) 24

(C) 30

(D) 54

(E) His age cannot be determined from the information given.

  8. Two printing presses working together can complete a job in 2.5 hours. Working alone, press A can do the job in 10 hours. How many hours will press B take to do the job by itself?

  9. Henry drove 100 miles to visit a friend. If he had driven 8 miles per hour faster than he did, he would 5 have arrived in  of the time he actually took. 6 How many minutes did the trip take?

(A) 100

(B) 120

(C) 125

(D) 144

(E) 150

10. Since 1950, when Martin graduated from high school, he has gained 2 pounds every year. In 1980 he was 40% heavier than in 1950. What percent of his 1995 weight was his 1980 weight?

(A) 80

(B) 85

(C) 87.5

(D) 90

(E) 95

Grid-in Questions

11. What is the greater of two numbers whose product is 900, if the sum of the two numbers exceeds their difference by 30?

12. The number of shells in Fred’s collection is 80% of the number in Phil’s collection. If Phil has 80 more shells than Fred, how many do they have altogether?

13. Karen played a game several times. She received $5 every time she won and had to pay $2 every time she lost. If the ratio of the number of times she won to the number of times she lost was 3:2, and if she won a total of $66, how many times did she play this game?

14. Each of the 10 players on the basketball team shot 100 free throws, and the average number of baskets made was 75. When the highest and lowest scores were eliminated, the average number of baskets for the remaining 8 players was 79. What is the smallest number of baskets anyone could have made?

15. In an office there was a small cash box. One day Ann took half of the money plus $1 more. Then Dan took half of the remaining money plus $1 more. Stan then took the remaining $11. How many dollars were originally in the box?

Answer Key

1. B   2. E   3. E   4. D

5. A   6. B   7. D   8. A

9. E 10. C

Answer Explanations

  1. B.    Judy’s average rate of reading is determined by dividing the total number of pages she read (200) by the total amount of time she spent reading. In the afternoon she read for  hours, and in the evening for hours, for a total time of hours.

Her average rate was

 pages per hour.

  2. E.    Let the five consecutive integers be n, n + 1, n + 2, n + 3, n + 4. Then:

Choice A,  is the smallest of the integers; the largest is

  3. E.    If there are b blue marbles, there are  Then,

  4. D.     If x represents the number of chocolate bars sold, then the number of lollipops sold is 150 – x. You must use the same units, so you can write 75 cents as 0.75 dollar or 74 dollars as 7400 cents. Avoid the decimals: xchocolates sold for 75x cents and (150 – x) lollipops sold for 40(150 – x) cents. Therefore:

  5. A.    Let x represent the number of students earning 100; then 85 – x is the number of students earning 75. Then:

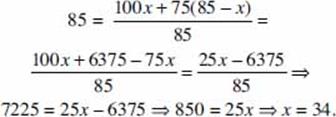
  6. B.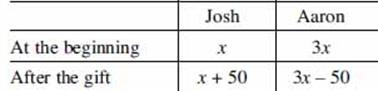    

After the gift, Josh will have 3 times as much money as Aaron:

So, 8x = 200  x = 25.

Therefore, Josh has $25 and Aaron has $75, for a total of $100.

  7. D.    Since  years ago Jason was 12, he is now  and  years from now, he will be  At that time he will be 2x years old, so 12 + x = 2x  x = 12. Thus, he is now 12 + 6 =18, and 3x, or 36, years from now he will be 18 + 36 = 54.

  8. A.    Let x represent the number of hours press B would take working alone.

        

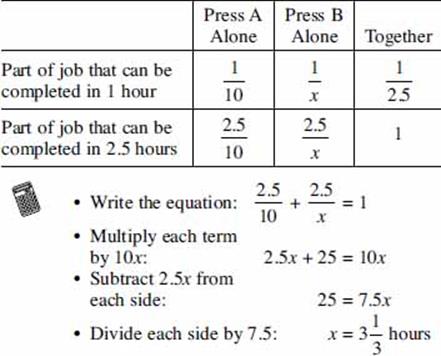
  9. E.    Let t represent the time, in hours, and r the rate, in miles per hour, that Henry drove. Then

Multiply the second equation by 

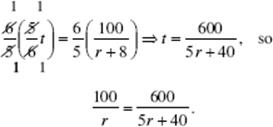
Cross-multiply:

500r + 4000 = 600r  100r = 4000  r = 40.

Henry drove at 40 miles per hour, and the trip took 100 ÷ 40 = 2.5 hours = 150 minutes. (Had he driven at 48 miles per hour, the trip would have taken 125 minutes.)

10. C.    Let x represent Martin’s weight in 1950. By 1980, he had gained 60 pounds (2 pounds per year for 30 years) and was 40% heavier:

60 = 0.40x  x = 60 ÷ 0.4 = 150.

 In 1980, he weighed 210 pounds, and 15 years later, in 1995, he weighed 240:

11. (60)    Let x be the greater and y the smaller of the two numbers; then

and, since xy = 900, x = 900 ÷ 15 = 60.

12. (720)    If x represents the number of shells in Phil’s collection, then Fred has .80x shells. Since Phil has 80 more shells than Fred:

So, x = 80 ÷ .20 = 400.
Then Phil has 400 shells and Fred has (.80) × 400 = 320 shells: a total of 720 shells.

13. (30)    Use TACTIC D1: write the letter x after each number in the ratio. Karen won 3x times and lost 2x times, and thus played a total of 5x games. Since she got $5 every time she won, she received $5(3x) = $15x. Also, since she paid $2 for each loss, she paid out $2(2x) = $4x. Therefore, her net winnings were $15x – $4x = $11x, which you are told was $66. Then, 11x = 66  x = 6, and so 5x = 30.

14. (18)     Since the average for all 10 players was 75, the total number of baskets made was

10 × 75 = 750. Also, since 8 of the players had an average of 79, they made a total of 8 × 79 = 632 baskets. The other 2 players, therefore, made 750 – 632 = 118 baskets. The most baskets that the player with the highest number could have made was 100, so the player with the lowest number had to have made at least 18.

15. (50)    You can avoid some messy algebra by working backwards. Put back the $11 Stan took; then put back the extra $1 that Dan took. There is now $12, which means that, when Dan took his half, he took $12. Put that back. Now there is $24 in the box. Put back the extra $1 that Ann took. The box now has $25, so before Ann took her half, there was $50. Algebraic solution. Assume that there were originally x dollars in the box. Ann took  Dan then took  of that plus $1 more; he took

Then Stan took $11. Since together they took all x dollars:

Therefore, 

GEOMETRY

Although about 30% of the math questions on the SAT involve geometry, you need to know only a relatively small number of facts—far less than you would learn in a geometry course—and, of course, you need provide no proofs. The next six sections review all of the geometry that you need to know to do well on the SAT. Also, the material is presented exactly as it appears on the SAT, using the same vocabulary and notation, which may be slightly different from the terminology you have used in your math classes. There are plenty of sample multiple-choice and grid-in problems for you to solve, and they will show you exactly how these topics are treated on the SAT.

9-I Lines and Angles

On the SAT, lines are usually referred to by lowercase letters, typically , m, and n. If P and Q are any points on line , we can also refer to  as PQ. In general, we have the following notations:

• PQ represents the line that goes through P and Q:

• PQ represents a ray; it consists of point P and all the points on PQ that are on the same side of P as Q:

•  represents a line segment (often referred to simply as a segment); it consists of points P and Q and all the points on PQ that are between them:

• PQ represents the length of segment .

If  and  have the same length, we say that  and  are congruent, and write  We can also write AB = PQ.

NOTE

AB ≅ PQ means exactly the same thing as AB = PQ.

An angle is formed by the intersection of two line segments, rays, or lines. The point of intersection is called the vertex.

An angle can be named by three points: a point on one side, the vertex, and a point on the other side. When there is no possible ambiguity, the angle can be named just by its vertex. For example, in the diagram below we can refer to the angle on the left as B or ABC. To talk about E, on the right, however, would be ambiguous; E might mean DEF or FEG or DEG.

NOTE

A ≅ B means exactly the same thing as mA = mB.

On the SAT, angles are always measured in degrees. The degree measure of ABC is represented by mABC. If P and Q have the same measure, we say that they are congruent and write  In the diagram below, A and B at the left are right angles. Therefore, mA = 90 and mB = 90, so mA = mB and  In equilateral triangle PQR, at the right, mP = mQ = mR = 60, and 

Key Fact I1

Angles are classified according to their degree measures.

• An acute angle measures less than 90°.
• A right angle measures 90°.
• An obtuse angle measures more than 90° but less than 180°.
• A straight angle measures 180°.

NOTE

A small square like the one in the second figure always means that the angle is a right angle. On the SAT, if an angle has a square, it must be a 90° angle, even if the figure has not been drawn to scale.

Key Fact I2

If two or more angles form a straight angle, the sum of their measures is 180°.

KEY FACT I2 is one of the facts provided in the “Reference Information” at the beginning of each math section.

EXAMPLE 1

In the figure below, R, S, and T are all on line  . What is the average (arithmetic mean) of a, b, c, d, and e?

Solution. Since RST is a straight angle, by KEY FACT I2, the sum of a, b, c, d, and e is 180, and so their average is 

In the figure below, since a + b + c + d = 180 and e + f + g = 180, a + b + c + d + e + f + g = 180 + 180 = 360.

It is also true that in the diagram below u + v + w + x + y + z = 360, even though none of the angles forms a straight angle.

Key Fact I3

The sum of the measures of all the angles around a point is 360°.

NOTE: This fact is particularly important when the point is the center of a circle, as will be seen in Section 9-L.

REFERENCE FACT

KEY FACT I3 is one of the facts provided in the “Reference Information” at the beginning of each math section.

When two lines intersect, four angles are formed. The two angles in each pair of opposite angles are called vertical angles.

Key Fact I4

Vertical angles are congruent.

NOTE

KEY FACT I4 means that if A and B are vertical angles, then mA = mB.

EXAMPLE 2

In the figure below, what is the value of a?

Solution. Because vertical angles are congruent:

a + 2b = 3a  2b = 2a  a = b.

For the same reason, b = c. Therefore, a, b, and c are all equal. Replace each b and c in the figure with a, and add:

a + a + 3a + a + 2a = 360  8a = 360  a = 45.

Consider these vertical angles:

By KEY FACT I4, a = c and b = d.

By KEY FACT I2, a + b = 180, b + c = 180, c + d = 180, and a + d = 180.

It follows that, if any of the four angles is a right angle, all the angles are right angles.

EXAMPLE 3

In the figure above, what is the value of x?

(A) 6
(B) 8 
(C) 10 
(D) 20 
(E) 40

Solution. Since vertical angles are congruent:

3x + 10 = 5(x – 2)  3x + 10 = 5x – 10  3x + 20 = 5x  20 = 2x  x = 10 (C).

In the figures below, line  divides ABC into two congruent angles, and line k divides line segment  into two congruent segments. Line  is said to bisect the angle, and line k bisects the line segment. Point M is called the midpoint of segment 

EXAMPLE 4

In the figure above, lines k, , and m intersect at O. If line m bisects AOB, what is the value of x?

Solution. Here, mAOB + 130 = 180  mAOB = 50; and since AOB is bisected, x = 25.

Two lines that intersect to form right angles are said to be perpendicular.

Two lines that never intersect are said to be parallel. Consequently, parallel lines form no angles. However, if a third line, called a transversal, intersects a pair of parallel lines, eight angles are formed, and the relationships among these angles are very important.

Key Fact I5

If a pair of parallel lines is cut by a transversal that is perpendicular to the parallel lines, all eight angles are right angles.

Key Fact I6

If a pair of parallel lines is cut by a transversal that is not perpendicular to the parallel lines:

• Four of the angles are acute, and four are obtuse.

• All four acute angles are congruent: a = c = e = g.

• All four obtuse angles are congruent: b = d = f = h.

• The sum of any acute angle and any obtuse angle is 180°: for example, d + e = 180, c + f = 180, b + g = 180,....

Helpful Hint

You must know KEY FACT I6— almost every SAT has questions based on it. However, you do not need to know the special terms you learned in your geometry class for these pairs of angles; those terms are not used on the SAT.

Key Fact I7

If a pair of lines that are not parallel is cut by a transversal, none of the statements listed in KEY FACT I6 is true.

Key Fact I8

If a line is perpendicular to each of a pair of lines, then these lines are parallel.

EXAMPLE 5

Note: Figure not drawn to scale

What is the value of x in the figure above?

(A) 40 
(B) 50 
(C) 90 
(D) 140 
(E) It cannot be determined from the information given.

Solution. Despite the fact that the figure has not been drawn to scale, the little squares assure you that the vertical line is perpendicular to both of the horizontal ones, so these lines are parallel. Therefore, the sum of the 140° obtuse angle and the acute angle marked x° is 180°:
x + 140 = 180  x = 40 (A).

NOTE: If the two little squares indicating right angles were not in the figure, the answer would be E: “It cannot be determined from the information given.” You are not told that the two lines that look parallel are actually parallel; and since the figure is not drawn to scale, you certainly cannot make that assumption. If the lines are not parallel, then 140 + x is not 180, and x cannot be determined.

EXAMPLE 6

In the figure above,  is parallel to two little squares indicating right angles were  What is the value of x?

Solution. Let y be the measure of BED. Then by KEY FACT I2:

37 + 90 + y = 180  127 + y = 180  y = 53.

Since  is parallel to  by KEY FACT I6, x = y  x = 53.

EXAMPLE 7

In the figure above, lines  and k are parallel. What is the value of a + b?

(A) 45
(B) 60
(C) 90
(D) 135
(E) It cannot be determined from the information given.

Solution. If you were asked for the value of either a or b, the answer would be E—neither one can be determined; but if you are clever, you can find the value of a + b. Draw a line parallel to  and k through the vertex of the angle. Then, looking at the top two lines, you see that a = x, and looking at the bottom two lines, you have b = y. Therefore, a + b = x + y = 45 (A).

Alternative solution. Draw a different line and use a fact from Section 9-J on triangles. Extend one of the line segments to form a triangle. Since  and k are parallel, the measure of the bottom angle in the triangle equals a. Now, use the fact that the sum of the measures of the three angles in a triangle is 180° or, even easier, that the given 45° angle is an exterior angle, and so is equal to the sum of a and b.

Exercises on Lines and Angles

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

  1. In the figure below, what is the value of b?

(A)   9

(B) 18

(C) 27

(D) 36

(E) 45

  2. In the figure below, what is the value of x if y:x = 3:2?

(A) 18

(B) 27

(C) 36

(D) 45

(E) 54

  3. What is the measure of the angle formed by the minute and hour hands of a clock at 1:50?

(A)   90°

(B)   95°

(C) 105°

(D) 115°

(E) 120°

  4. Concerning the figure below, if a = b, which of the following statements must be true?

Note: Figure not drawn to scale

  I. c = d.

 II.  and k are parallel.

III. m and  are perpendicular.

(A) None

(B) I only

(C) I and II only

(D) I and III only

(E) I, II, and III

  5. In the figure below, B and C lie on line n, m bisects AOC, and  bisects AOB. What is the measure of DOE?

Note: Figure not drawn to scale

(A)   75°

(B)   90°

(C) 105°

(D) 120°

(E) It cannot be determined from the information given.

Grid-in Questions

  6. In the figure below, what is the value of 

  7. In the figure below, a:b = 3:5 and c:b = 2:1. What is the measure of the largest angle?

Note: Figure not drawn to scale

  8. A, B, and C are points on a line, with B between A and C. Let M and N be the midpoints of  and , respectively. If AB:BC = 3:1, what is AB:MN?

  9. In the figure below, lines k and  are parallel. What is the value of y – x?

10. In the figure below, what is the average (arithmetic mean) of the measures of the five angles?

Answer Key

1. D   2. C   3. D   4. B   5. B

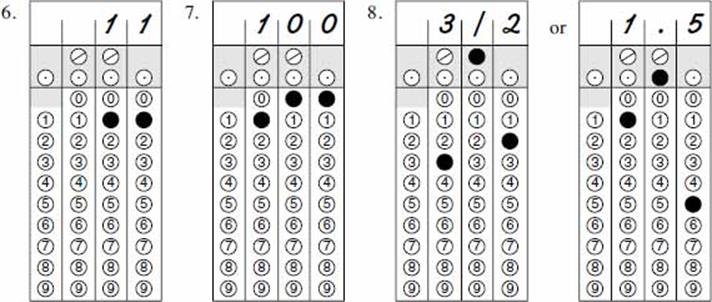
Answer Explanations

  1. D.    Since vertical angles are congruent, the measures of the two unmarked angles are 2b° and 4a°. Also, since the sum of all six angles is 360°:

360 = 4a + 2b + 2a + 4a + 2b + b = 10a + 5b.

Note that since the angles labeled a and 2b are vertical angles, b = 2a, and so 5b = 10a. Hence:

360 = 10a + 5b = 10a + 10a = 20a  a = 18  b = 36.

  2. C.    Since x + y + 90 = 180, then x + y = 90. Also, since y:x = 3:2, then y = 3t and x = 2t. Therefore:

  3. D.    For problems such as this, always draw a diagram. The measure of each of the 12 central angles from one number to the next on the clock is 30°. At 1:50 the minute hand is pointing at 10, and the hour hand has gone of the way from 1 to 2. Then, from 10 to 1 on the clock is 90°, and from 1 to the hour hand is  for a total of 90° + 25° = 115°.

  4. B.    No conclusion can be drawn about the lines; they could form any angles whatsoever. (II and III are both false.) Statement I is true: c = 180 – a = 180 – b = d.

5. B. 

  6. (11)    From the diagram, you see that 6a = 180, which implies that a = 30, and that 5b = 180, which implies that b = 36. Therefore:

  7. (100)    Since a:b = 3:5, then for some number x, a = 3x and b = 5x; and since c:b = 2:1, then c = 2b = 10x. Then:

3x + 5x + 10x = 180  18x = 180.

So, x = 10 and c = 10x = 10(10) = 100.

  8.     If a diagram is not provided on a geometry question, draw one. Since AB:BC = 3:1, let AB = 3 and BC = 1.

From the figure above, you can see that AB:MN 

  9. (45)    Since lines  and k are parallel, the angle marked y in the given diagram and the sum of the angles marked x and 45 are equal:
y = x + 45  y – x = 45.

10. (72)    The markings in the five angles are irrelevant. The sum of the measures of these angles is 360°, and 360 ÷ 5 = 72. If you calculated the measure of each angle, you should have gotten 36, 54, 72, 90, and 108; but you would have wasted time.

9-J Triangles

More geometry questions on the SAT pertain to triangles than to any other topic. To answer these questions correctly, you need to know several important facts about the angles and sides of triangles. The KEY FACTS in this section are extremely useful. Read them carefully, a few times if necessary, and make sure you learn them all.

Key Fact J1

In any triangle, the sum of the measures of the three angles is 180°.

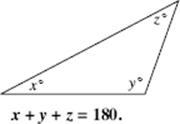
Figure 1 illustrates KEY FACT J1 for five different triangles, which will be discussed below.

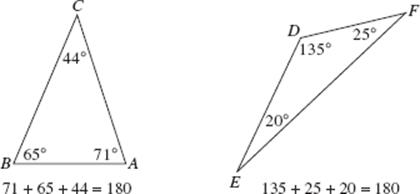
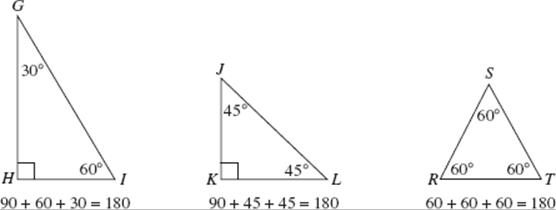
FIGURE 1

REFERENCE FACT

KEY FACT J1 is one of the facts provided in the “Reference Information” at the beginning of each math section.

EXAMPLE 1

In the figure below, what is the value of x?

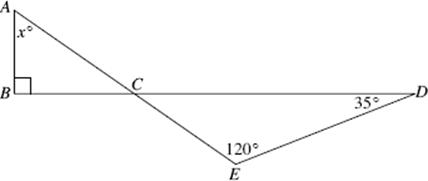
Solution. Use KEY FACT J1 twice: first, for CDE and then for ABC.

• mDCE + 120 + 35 = 180  mDCE + 155 = 180  mDCE = 25.

• Since vertical angles are congruent, mACB = 25 (see KEY FACT I4).

• x + 90 + 25 = 180  x + 115 = 180  x = 65.

EXAMPLE 2

In the figure above, what is the value of a?

Solution. First find the value of b:

180 = 45 + 75 + b = 120 + b  b = 60.

Then, a + b = 180  a = 180 – b = 180 – 60 = 120.

In Example 2, BCD, which is formed by one side of ABC and the extension of another side, is called an exterior angle. Note that, to find a, you did not have to first find b; you could just have added the other two angles: a = 75 + 45 = 120. This is a useful fact to remember.

Key Fact J2

The measure of an exterior angle of a triangle is equal to the sum of the measures of the two opposite interior angles.

Key Fact J3

In any triangle:

• the longest side is opposite the largest angle;

• the shortest side is opposite the smallest angle;

• sides with the same length are opposite angles with the same measure.

CAUTION: In KEY FACT J3 the condition “in any triangle” is crucial. If the angles are not in the same triangle, none of the conclusions holds. For example, in Figure 2 below AB, and DE are not equal even though each is opposite a 90° angle; and in Figure 3, QS is not the longest side even though it is opposite the largest angle.

FIGURE 2

FIGURE 3

Consider triangles ABC, JKL, and RST in Figure 1.

• In ABC: BC is the longest side since it is opposite A, the largest angle (71°). Similarly, AB is the shortest side since it is opposite C, the smallest angle (44°). Therefore, AB < AC < BC.

• In JKL: Angles J and L have the same measure (45°), so JK = KL.

• In RST: Since all three angles have the same measure (60°), all three sides have the same length: RS = ST = TR.

EXAMPLE 3

In the figure above, which of the following statements concerning the length of side YZ is true?

(A) YZ < 8

(B) YZ = 8

(C) 8 < YZ < 10

(D) YZ = 10

(E) YZ > 10

Solution.

• By KEY FACT J1, mX + 71 + 49 = 180  mX = 60.

• Then Y is the largest angle, Z is the smallest, and X is in between.

• Therefore, by KEY FACT J3: XY < YZ < XZ  8 < YZ < 10.

• The answer is C.

Classification of Triangles

Acute triangles are triangles such as ABC and RST, in which all three angles are acute. An acute triangle can be scalene, isosceles, or equilateral.

Obtuse triangles are triangles such as DEF, in which one angle is obtuse and two are acute. An obtuse triangle can be scalene or isosceles.

Right triangles are triangles such as GHI and JKL, which have one right angle and two acute ones. A right triangle can be scalene or isosceles. The side opposite the 90° angle is called the hypotenuse, and by KEY FACT J3 it is the longest side. The other two sides are called the legs.

If x and y are the measures of the acute angles of a right triangle, then by KEY FACT J1: 90 + x + y = 180, and so x + y = 90.

Key Fact J4

In any right triangle, the sum of the measures of the two acute angles is 90°.

EXAMPLE 4

In the figure above, what is the average (arithmetic mean) of x and y?

Solution. Since the diagram indicates that ABC is a right triangle, then, by KEY FACT J4, x + y = 90. Therefore, the average of x and y 

The most important facts concerning right triangles are the Pythagorean theorem and its converse, which are given in KEY FACT J5 and repeated as the first line of KEY FACT J6.

Key Fact J5

Let a, b, and c be the sides of ABC, with a ≤ b ≤ c.

• If ABC is a right triangle, a² + b² = c²;

• If a² + b² = c², then ABC is a right triangle.

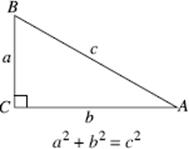
REFERENCE FACT

The Pythagorean theorem is one of the facts provided in the “Reference Information” at the beginning of each math section.

Key Fact J6

Let a, b, and c be the sides of ABC, with a ≤ b ≤ c.

• a² + b² = c² if and only if C is a right angle.

• a² + b² < c² if and only if C is obtuse.

• a² + b² > c² if and only if C is acute.

EXAMPLE 5

Which of the following CANNOT be the lengths of the sides of a right triangle?

(A) 3, 4, 5

(B) 1, 1, 

(C) 1, , 2

(D) 

(E) 30, 40, 50

Solution. Just check the choices.

• (A): 32 + 42 = 9 + 16 = 25 = 52	These are the lengths of the sides of a right triangle.
• (B): 12 + 12 = 1 + 1 = 2 =	These are the lengths of the sides of a right triangle.
• (C): 12 +  = 1 + 3 = 4 = 22	These are the lengths of the sides of a right triangle.
• (D):  = 3 + 4 = 7	These are not the lengths of the sides of a right triangle.

Stop. The answer is D. There is no need to check choice E—but if you did, you would find that 30, 40, 50 are the lengths of the sides of a right triangle.

Below are the right triangles that appear most often on the SAT. You should recognize them immediately whenever they come up in questions. Carefully study each one, and memorize KEY FACTS J7–J11.

On the SAT, the most common right triangles whose sides are integers are the 3-4-5 right triangle (A) and its multiples (B).

Key Fact J7

For any positive number x, there is a right triangle whose sides are 3x, 4x, 5x.

For example:

x = 1            3, 4, 5

x = 2            6, 8, 10

x = 3            9, 12, 15

x = 4            12, 16, 20

x = 5            15, 20, 25

x = 10          30, 40, 50

x = 50          150, 200, 250

x = 100        300, 400, 500

NOTE: KEY FACT J6 applies even if x is not an integer. For example:

x = 0.5          1.5, 2, 2.5

x =            3, 4, 5

The only other right triangle with integer sides that you should recognize immediately is the one whose sides are 5, 12, 13 (C).

Let x = length of each leg, and h = length of the hypotenuse, of an isosceles right triangle (D).
By the Pythagorean theorem,

x² + x² = h²  2x² = h²  h = 

Key Fact J8

In a 45-45-90 right triangle, the sides are x, x, and x. Therefore:

• By multiplying the length of a leg by , you get the hypotenuse.

• By dividing the hypotenuse by , you get the length of each leg.

REFERENCE FACT

KEY FACT J8 is one of the facts provided in the “Reference Information” at the beginning of each math section.

Key Fact J9

The diagonal of a square divides the square into two isosceles right triangles.

The last important right triangle is the one whose angles measure 30°, 60°, and 90°.

Key Fact J10

An altitude divides an equilateral triangle into two 30-60-90 right triangles.

Let 2x be the length of each side of equilateral triangle ABC, in which altitude AD is drawn.

Then ADB is a 30-60-90 right triangle, and its sides are x, 2x, and h. By the Pythagorean theorem, 

Key Fact J11

In a 30-60-90 right triangle the sides are x, x , and 2x.

If you know the length of the shorter leg (x):

• multiply it by  to get the length of the longer leg;

• multiply it by 2 to get the length of the hypotenuse.

If you know the length of the longer leg (a):

• divide it by  to get the length of the shorter leg;

• multiply the shorter leg by 2 to get the length of the hypotenuse.

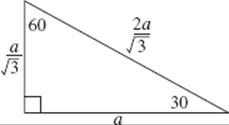
If you know the length of the hypotenuse (h):

• divide it by 2 to get the length of the shorter leg;

• multiply the shorter leg by  to get the length of the longer leg.

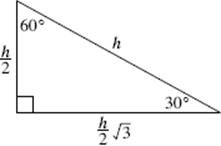
REFERENCE FACT

KEY FACT J11 is one of the facts provided in the “Reference Information” at the beginning of each math section.

EXAMPLE 6

What is the area of a square whose diagonal is 10?

(A)   20

(B)   40

(C)   50

(D) 100

(E) 200

Solution. Draw a diagonal in a square of side s, creating a 45-45-90 right triangle. By KEY FACT J8:

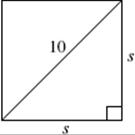
The answer is C.

[KEY FACT K8 gives the formula for the area of a square based on this example:  where d is the length of a diagonal.]

EXAMPLE 7

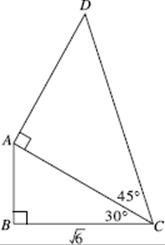
In the diagram above, if BC = , what is the value of CD?

Helpful Hint

If you know some elementary trigonometry, you could use the sine, cosine, and tangent ratios to solve questions involving 30-60-90 triangles and 45-45-90 triangles. But YOU SHOULDN’T. Rather, you should use KEY FACTS J8 and J11. You should know these facts by heart; but in case you forget, they are given to you in the Reference Information on the first page of each math section.

Solution. ABC and DAC are 30-60-90 and 45-45-90 right triangles, respectively. Use KEY FACTS J11 and J8.

• Divide BC, the length of the longer leg, by  to get AB, the length of the shorter leg:

• Multiply AB by 2 to get the length of the hypotenuse: AC = 2 .

• Since AC is also a leg of isosceles right triangle DAC, to get the length of hypotenuse CD, multiply AC by 

Key Fact J12    Triangle Inequality

The sum of the lengths of any two sides of a triangle is greater than the length of the third side.

The best way to remember this is to see that, in ABC, x + y, the length of the path from A to C through B, is greater than z, the length of the direct path from A to C.

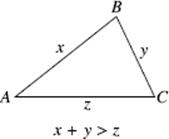
NOTE: If you subtract x from each side of x + y > z, you see that z – x < y.

Helpful Hint

Almost every SAT has at least one question whose solution requires you to use the triangle inequality. Be sure you know KEY FACTS J12 and J13.

Key Fact J13

The difference between the lengths of any two sides of a triangle is less than the length of the third side.

EXAMPLE 8

NOTE

If a and b are the lengths of two sides of a triangle with a > b, then any number greater than a – b and less than a + b could be the length of the third side.

If the lengths of two sides of a triangle are 6 and 7, which of the following could be the length of the third side?

  I. 1

 II. 5

III. 15

(A) None

(B) I only

(C) II only

(D) I and II only

(E) I, II, and III

Solution. Use KEY FACTS J12 and J13.

• The length of the third side must be less than 6 + 7 = 13. (III is false.)

• The length of the third side must be greater than 7 – 6 = 1. (I is false.)

• Any number between 1 and 13 could be the length of the third side. (II is true.)

The answer is C.

The following diagram illustrates several triangles two of whose sides have lengths of 6 and 7.

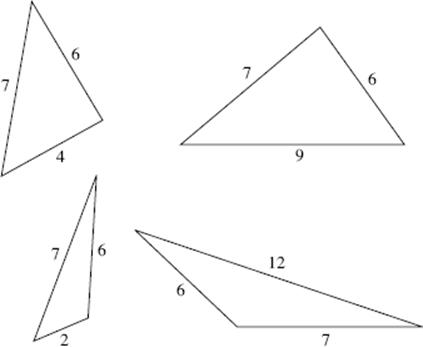
On the SAT, two other terms that appear regularly in triangle problems are perimeter and area (see Section 9-K).

EXAMPLE 9

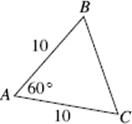
In the figure above, what is the perimeter of ABC?

Solution. First, use KEY FACTS J3 and J1 to find the measures of the angles.

• Since AB = AC, mB = mC. Represent each measure by x.

• Then, x + x + 60 = 180  2x = 120  x = 60.

• Since the measure of each angle of ABC is 60°, the triangle is equilateral.

• Then, BC = 10, and the perimeter is 10 + 10 + 10 = 30.

Key Fact J14

The area of a triangle is given by  where b = base and h = height.

NOTE:

1. Any side of the triangle can be taken as the base.

2. The height is a line segment drawn perpendicular to the base from the opposite vertex.

3. In a right triangle, either leg can be the base and the other the height.

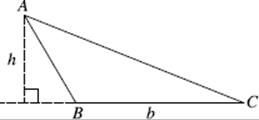
4. The height may be outside the triangle. [See the figure above.]

In the figure above:

• If AC is the base, BD is the height.

• If AB is the base, CE is the height.

• If BC is the base, AF is the height.

REFERENCE FACT

KEY FACT J14 is one of the facts provided in the “Reference Information” at the beginning of each math section.

EXAMPLE 10

What is the area of an equilateral triangle whose sides are 10?

(A) 30

(B) 25 

(C) 50

(D) 50 

(E) 100

Solution. Draw an equilateral triangle and one of its altitudes.

• By KEY FACT J10, ADB is a 30-60-90 right triangle.

• By KEY FACT J11, BD = 5 and AD = 5.

• The area of ABC = (10)(5) = 25  (B).

Replacing 10 by s in Example 10 yields a very useful result.

Key Fact J15

If A represents the area of an equilateral triangle with side s, then 

Two triangles, such as I and II in the figure below, that have the same shape, but not necessarily the same size, are said to be similar.

KEY FACT J16 makes this intuitive definition mathematically precise.

Key Fact J16

Two triangles are similar provided that the following two conditions are satisfied.

1. The three angles in the first triangle are congruent to the three angles in the second triangle.

2. The lengths of the corresponding sides of the two triangles are in proportion:

NOTE: Corresponding sides are sides opposite angles of the same measure.

An important theorem in geometry states that, if condition 1 in KEY FACT J16 is satisfied, then condition 2 is automatically satisfied. Therefore, to show that two triangles are similar, it is sufficient to show that their angles have the same measure. Furthermore, if the measures of two angles of one triangle are equal to the measures of two angles of a second triangle, then the measures of the third angles are also equal. This is summarized in KEY FACT J17.

Key Fact J17

If the measures of two angles of one triangle are equal to the measures of two angles of a second triangle, the triangles are similar.

EXAMPLE 11

In the diagram above, what is BC?

Solution. Since vertical angles are congruent, mECD = mACB. Also, mA = mE since both A and E are right angles. Then the measures of two angles of CAB are equal to the measures of two angles of CED, and by KEY FACT J17, the two triangles are similar. Finally, by KEY FACT J16, corresponding sides are in proportion. Therefore:

If two triangles are similar, the common ratio of their corresponding sides is called the ratio of similitude.

Key Fact J18

If two triangles are similar, and if k is the ratio of similitude, then:

• The ratio of all the linear measurements of the triangles is k.

• The ratio of the areas of the triangles is k².

In the figure below, ABC and PQR are similar with mC = mR.

Then AB and PQ are corresponding sides, and the ratio of similitude is 

Therefore,

• All the sides are in the ratio of 3:1:

BC = 3 × QR,

AC = 3 × PR.

• The altitudes are in the ratio of 3:1:

BD = 3 × QS.

• The perimeters are in the ratio of 3:1:

Perimeter of ABC = 3 × (perimeter of PQR).

• The areas are in the ratio of 9:1:

Area of ABC = 9 × (area of PQR).

Exercises on Triangles

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

1.   In the triangle above, what is the value of x?

(A) 20

(B) 30

(C) 40

(D) 50

(E) 60

2.   What is the area of an equilateral triangle whose altitude is 6?

(A) 18

(B) 12 

(C) 18 

(D) 36

(E) 24 

3.   Two sides of a right triangle are 12 and 13. Which of the following could be the length of the third side?

  I. 5

 II. 11

III. 

(A) I only

(B) II only

(C) I and II only

(D) I and III only

(E) I, II, and III

4.   What is the smallest integer, x, for which x, x + 5, and 2x – 15 can be the lengths of the sides of a triangle?

(A)   8

(B)   9

(C) 10

(D) 11

(E) 12

5.   What is the value of x in the figure above?

(A)   80

(B) 100

(C) 115

(D) 120

(E) 130

6.   What is the value of PS in the triangle above?

(A) 5 

(B) 10

(C) 11

(D) 13

(E) 12 

Questions 7 and 8 refer to the following figure.

7.   What is the area of BED?

(A) 12

(B) 24

(C) 36

(D) 48

(E) 60

8.   What is the perimeter of BED?

(A) 19 + 5

(B) 28

(C) 17 + 

(D) 32

(E) 36

Questions 9 and 10 refer to the following figure.

9.   What is the area of DFH?

(A) 3

(B) 4.5

(C) 6

(D) 7.5

(E) 10

10. What is the perimeter of DFH?

(A) 

(B) 

(C) 16

(D) 17

(E) 18

Questions 11 and 12 refer to the following figure.

11. What is the perimeter of ABC?

(A) 48

(B) 

(C) 

(D) 72

(E) It cannot be determined from the information given.

12. What is the area of ABC?

(A) 108

(B) 

(C) 

(D) 198

(E) It cannot be determined from the information given.

13. Which of the following expresses a true relationship between x and y in the figure above?

(A) y = 60 – x

(B) y = x

(C) x + y = 90

(D) y = 180 – 3x

(E) x = 90 – 3y

Questions 14 and 15 refer to the following figure, in which rectangle ABCD is divided into two 30-60-90 triangles, a 45-45-90 triangle, and shaded triangle ABF.

14. What is the perimeter of shaded triangle ABF?

(A) 

(B) 

(C) 

(D) 

(E) 

15. What is the area of shaded triangle ABF?

(A) 

(B) 1

(C) 

(D) 

(E) 

Grid-in Questions

16. If the difference between the measures of the two smaller angles of a right triangle is 20°, what is the measure, in degrees, of the smallest angle?

Questions 17 and 18 refer to the figure below.

17. What is the perimeter of ABC?

18. What is the area of ABC?

19. Reanna and Jason each drew a triangle. Both triangles have sides of length 10 and 20, and the length of the third side of each triangle is an integer. What is the greatest possible difference between the perimeters of the two triangles?

20. If the measures of the angles of a triangle are in the ratio of 1:2:3, and if the perimeter of the triangle is 30 + 10, what is the length of the smallest side?

Answer Key

1. D   2. B   3. D   4. D   5. C

6. D   7. B   8. D   9. B 10. B

11. C 12. C 13. A 14. E 15. B

Answer Explanations

  1. D.    x + 2x + 30 = 180  3x + 30 = 180  3x = 150  x = 50.

  2. B.    Sketch and label equilateral triangle ABC, and draw in altitude AD, whose length is given as 6.

By KEY FACT J11:

Since BD is one-half the base of the triangle, the area is 2 × 6 = 12.

  3. D.    If the triangle were not required to be right, by KEY FACTS J11 and J12 any number greater than 1 and less than 25 could be the length of the third side. For a right triangle, however, there are only two possibilities.

• If 13 is the hypotenuse and one of the legs is 12, then the other leg is 5. (I is true.) (If you didn’t recognize the 5-12-13 triangle, use the Pythagorean theorem: 12² + x² = 13², and solve.)

• If 12 and 13 are the lengths of the two legs, then use the Pythagorean theorem to find the length of the hypotenuse:

So, 

(III is true.)

Since  an 11-12-13 triangle is not a right triangle. (II is false.)

  4. D.    In a triangle the sum of the lengths of any two sides must be greater than the third side. For x + (x + 5) to be greater than 2x – 15, 2x + 5 must be greater than 2x – 15; but that’s always true. For x + (2x – 15) to be greater than x + 5, 3x – 15 must be greater than x + 5; but 3x – 15 > x + 5 is true only if 2x > 20, which means x > 10. The smallest integer value of x is 11.

  5. C.    Label the other angles:

50 + a + b = 180  a + b = 130,

and since the triangle is isosceles, a = b. Therefore, a and b are each 65, and x = 180 – 65 = 115.

  6. D.    Use the Pythagorean theorem twice, unless you recognize the common right triangles in this figure (which you should). Since PR = 20 and QR = 16, PQR is a 3x-4x-5x right triangle with x = 4. Then PQ = 12, and PQSis a right triangle whose legs are 5 and 12. The hypotenuse, PS, therefore, is 13. [If you had difficulty with this question, review the material, but in the meantime remember TACTIC 2: trust the diagram.  is longer than , so you can eliminate A, B, and C, and  is clearly shorter than , so eliminate E.]

  7. B.    You could calculate the area of the rectangle and subtract the areas of the two white right triangles, but don’t. If BE is the base of BED, DC is the height.

The area is 

  8. D.    Since both BD and ED are the hypotenuses of right triangles, their lengths can be calculated by the Pythagorean theorem, but again these are triangles you should recognize: the sides of DCE are 5-12-13, and those of BAD are 9-12-15 (3x-4x-5x, with x = 3). Therefore, the perimeter of BED is 4 + 13 + 15 = 32.

  9. B.    Since DGH is a right triangle, whose hypotenuse is 5 and one of whose legs is 3, the other leg, GH, is 4. Since GF = DE = 7, HF = 3. Now, DFH has a base of 3 (HF) and a height of 3 (DG), and its area is (3)(3) = 4.5.

10. B.    For DFH, you already have that DH = 5 and HF = 3; you need only find DF, which is the hypotenuse of DEF. By the Pythagorean theorem,

So, 

The perimeter is 

11. C.    Triangle ADB is a right triangle whose hypotenuse is 15 and one of whose legs is 9, so this is a 3x-4x-5x triangle with x = 3, and AD = 12. Now ADC is a 30-60-90 triangle, whose shorter leg is 12. Hypotenuse AC is 24, and leg CD is 12, so the perimeter is

12. C.    From the solution to Exercise 11, you have the base (9 + 12) and the height (12) of ABC. Then, the area is

13. A.    x + 2x + 3y = 180  3x + 3y = 180  x + y = 60  y = 60 – x.

14. E.

You are given enough information to determine the sides of all the triangles. Both 30-60-90 triangles have sides 1, , 2; and the 45-45-90 triangle has sides 2, 2, 2 . Also,

AB = CD = 1 + , and
BF = AD – CF=  – 1.
Then, the perimeter of the shaded triangle is 

15. B.    The area of ABF = ( + 1) ( – 1) = (3 – 1) = (2) = 1.

16. (35)

• Draw a diagram and label it. Let x be the measure of the larger angle and y be the measure of the smaller angle.

Then,

• Add the equations:

Then x = 55, and y = 90 – 55 = 35.

17. (100)  By the Pythagorean theorem, 8² + 15² = (CE)²  (CE)² = 64 + 225 = 289.
So, CE=  = 17.
Then the perimeter of CDE is 8 + 15 + 17 = 40.
Triangles ABC and CDE are similar (each has a 90° angle, and the vertical angles at C are congruent). The ratio of similitude is =  so the perimeter of ABC is 2.5 × 40 = 100.

18. (375) The area of CDE = (8)(15) = 60.
Since the ratio of similitude for the two triangles (as calculated in Solution 17) is 2.5, the area of ABC is (2.5)² times the area of CDE:
(2.5)² × 60 = 6.25 × 60 = 375.

19. (18) Assume a triangle has sides of length 10, 20, and x. Then, since the sum of the lengths of any two sides of a triangle is greater than the length of the third side, 

Since x must be an integer,  and the perimeter P satisfies  The greatest possible difference then between the two perimeters is 59 – 41 = 18.

20. (10) If the measures of the angles are in the ratio of 1:2:3, then:

x + 2x + 3x = 180  6x = 180  x = 30.

The triangle is a 30-60-90 right triangle, and the sides are a, 2a, and a . The perimeter therefore is 3a + a = a(3 + ), so a(3 + ) = 30 + 10 = 10(3 + ). So, a = 10.

9-K Quadrilaterals and Other Polygons

A polygon is a closed geometric figure made up of line segments. The line segments are called sides, and the endpoints of the line segments are called vertices (each one is a vertex). Line segments inside the polygon drawn from one vertex to another are called diagonals

The simplest polygons, which have three sides, are the triangles, which you studied in Section 9-J. A polygon with four sides is called a quadrilateral. There are special names (such as pentagon and hexagon) for polygons with more than four sides, but you do not need to know any of them for the SAT.

This section will present a few facts about polygons in general and then review the key facts you need to know about three special quadrilaterals.

Every quadrilateral has two diagonals. If you draw in either one, you will divide the quadrilateral into two triangles.

Since the sum of the measures of the three angles in each of the triangles is 180°, the sum of the measures of the angles in the quadrilateral is 360°.

Key Fact K1

In any quadrilateral, the sum of the measures of the four angles is 360°.

In exactly the same way as shown above, any polygon can be divided into triangles by drawing in all of the diagonals emanating from one vertex.

Notice that a five-sided polygon is divided into three triangles, and a six-sided polygon is divided into four triangles. In general, an n-sided polygon is divided into (n – 2) triangles, which leads to KEY FACT K2.

Key Fact K2

The sum of the measures of the n angles in a polygon with n sides is (n – 2) × 180°.

EXAMPLE 1

In the figure above, what is the value of x?

Solution. Since DEF is equilateral, all of its angles measure 60°; also, since the two angles at vertex D are vertical angles, their measures are equal. Therefore, the measure of D in quadrilateral ABCD is 60°. Also, A and C are right angles, so each measures 90°.

Finally, since the sum of the measures of all four angles of ABCD is 360°:

60 + 90 + 90 + x = 360  240 + x = 360  x = 120.

An exterior angle of a polygon is formed by extending a side. In the polygons below, one exterior angle has been drawn in at each vertex. Surprisingly, if you add the measures of all of the exterior angles in any of the polygons, the sums are equal.

Key Fact K3

In any polygon, the sum of the measures of the exterior angles, taking one at each vertex, is 360°.

EXAMPLE 2

A 10-sided polygon is drawn in which each angle has the same measure. What is the measure, in degrees, of each angle?

Solution 1. By KEY FACT K2, the sum of the degree measures of the 10 angles is (10 – 2) × 180 = 8 × 180 = 1440. Then, each angle is 1440 ÷ 10 = 144.

Solution 2. By KEY FACT K3, the sum of the degree measures of the 10 exterior angles is 360, so each one is 36. Therefore, the degree measure of each interior angle is 180 – 36 = 144.

A parallelogram is a quadrilateral in which both pairs of opposite sides are parallel.

Key Fact K4

Parallelograms have the following properties:

• Opposite sides are congruent: AB = CD and AD = BC.

• Opposite angles are congruent: a = c and b = d.

• Consecutive angles add up to 180°: a + b = 180, b + c = 180, c + d = 180, and a + d = 180.

• The two diagonals bisect each other: AE = EC and BE = ED.

• A diagonal divides the parallelogram into two triangles that have exactly the same size and shape. (The triangles are congruent.)

EXAMPLE 3

In the figure above, ABCD is a parallelogram. Which of the following statements must be true?

(A) x < y

(B) x = y

(C) x > y

(D) x + y < 90

(E) x + y > 90

Solution. Since AB and CD are parallel line segments cut by transversal BD, mABD = y. In ABD, AB > AD, so by KEY FACT J3 the measure of the angle opposite AB is greater than the measure of the angle opposite AD. Therefore, x > y (C).

A rectangle is a parallelogram in which all four angles are right angles. Two adjacent sides of a rectangle are usually called the length (  ) and the width (w). Note that the length is not necessarily greater than the width.

Key Fact K5

Since a rectangle is a parallelogram, all of the properties listed in KEY FACT K4 hold for rectangles. In addition:

• The measure of each angle in a rectangle is 90°.

• The diagonals of a rectangle are congruent: AC  BD.

A square is a rectangle in which all four sides have the same length.

Key Fact K6

Since a square is a rectangle, all of the properties listed in KEY FACTS K4 and K5 hold for squares. In addition:

• All four sides have the same length.

• Each diagonal divides the square into two 45-45-90 right triangles.

• The diagonals are perpendicular to each other: AC  BD.

EXAMPLE 4

What is the length of each side of a square if its diagonals are 10?

Solution. Draw a diagram. In square ABCD, diagonal AC is the hypotenuse of a 45-45-90 right triangle, and side AB is a leg of that triangle. By KEY FACT J7,

The perimeter (P) of any polygon is the sum of the lengths of all of its sides. The only polygons for which we have formulas for the perimeter are the rectangle and the square.

Key Fact K7

In a rectangle, P = 2( + w); in a square, P = 4s.

EXAMPLE 5

The length of a rectangle is twice its width. If the perimeter of the rectangle is the same as the perimeter of a square of side 6, what is the square of the length of a diagonal of the rectangle?

Solution. Don’t do anything until you have drawn diagrams.

Since the perimeter of the square is 24, the perimeter of the rectangle is also 24. Then

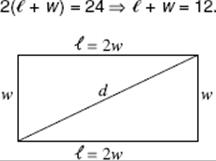
But  = 2w, so

2w + w = 3w = 12  w = 4 (and  = 8).

Finally, use the Pythagorean theorem:

d² = 4² + 8² = 16 + 64 = 80.

In Section 9-J you reviewed the formula for the area of a triangle. The only other polygons for which you need to know area formulas are the parallelogram, rectangle, and square.

• Parallelogram: Since the area of each of the two triangles formed by drawing a diagonal in a parallelogram is bh, the area of the parallelogram is twice as great:

• Rectangle: In a rectangle the same formula holds, but it is usually written as

A = w,

using the terms length and width instead of base and height.

• Square: In a square the length and width are equal; we label each of them s (side), and write A = s × s = s².

If d is the diagonal of a square,

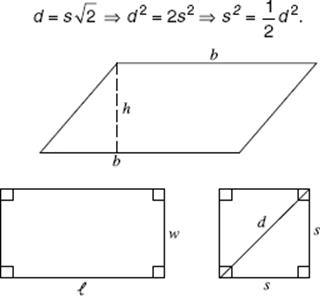
REFERENCE FACT

The formula for the area of a rectangle is one of the facts provided in the “Reference Information” at the beginning of each math section.

Key Fact K8

Here are the area formulas you need to know:

• For a parallelogram: A = bh.

• For a rectangle: A = w.

• For a square: A = s² or A = d²

EXAMPLE 6

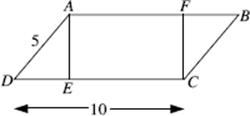
In the figure above, the area of parallelogram ABCD is 40. What is the area of rectangle AFCE?

(A) 20

(B) 24

(C) 28

(D) 32

(E) 36

Solution. Since the base, CD, is 10 and the area is 40, the height, AE, must be 4. Then AED must be a 3-4-5 right triangle with DE = 3, which implies that EC = 7. The area of the rectangle is 7 × 4 = 28 (C).

Exercises on Quadrilaterals and Other Polygons

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

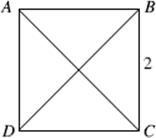
1.    In the figure above, the two diagonals divide square ABCD into four small triangles. What is the sum of the perimeters of those triangles?

(A) 2 + 2

(B) 8 + 4

(C) 8 + 8

(D) 16

(E) 24

2.    If the length of a rectangle is 4 times its width, and if its area is 144, what is its perimeter?

(A)   6

(B) 24

(C) 30

(D) 60

(E) 96

3.    If the angles of a five-sided polygon are in the ratio of 2:3:3:5:5, what is the degree measure of the smallest angle?

(A) 20

(B) 40

(C) 60

(D) 80

(E) 90

Questions 4 and 5 refer to a rectangle in which the length of each diagonal is 12, and one of the angles formed by the diagonal and a side measures 30°.

4.    What is the area of the rectangle?

(A) 18

(B) 72

(C) 18

(D) 36

(E) 36

5.    What is the perimeter of the rectangle?

(A) 18

(B) 24

(C) 12 + 12

(D) 18 + 6

(E) 24

6.    The length of a rectangle is 5 more than the side of a square, and the width of the rectangle is 5 less than the side of the square. If the area of the square is 45, what is the area of the rectangle?

(A) 20

(B) 25

(C) 45

(D) 50

(E) 70

Questions 7 and 8 refer to the following figure, in which M, N, O, and P are the midpoints of the sides of rectangle ABCD.

7.    What is the perimeter of quadrilateral MNOP?

(A) 24

(B) 32

(C) 40

(D) 48

(E) 60

8.    What is the area of quadrilateral MNOP?

(A)   48

(B)   60

(C)   72

(D)   96

(E) 108

Questions 9 and 10 refer to the following figure, in which M and N are midpoints of two of the sides of square ABCD.

9.    What is the perimeter of the shaded region?

(A) 3

(B) 2 + 3

(C) 3 + 2

(D) 5

(E) 8

10. What is the area of the shaded region?

(A) 1.5

(B) 1.75

(C) 3

(D) 2

(E) 3

Grid-in Questions

11. In the figure below, ABCD is a parallelogram. What is the value of y – z?

12. In the figure below, what is the sum of the degree measures of all of the marked angles?

13. If, in the figures below, the area of rectangle ABCD is 100, what is the area of rectangle EFGH?

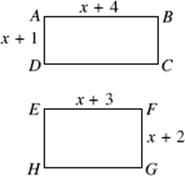
14. How many sides does a polygon have if the measure of each interior angle is 8 times the degree measure of each exterior angle?

15. In quadrilateral WXYZ, the measure of Z is 10 more than twice the average of the measures of the other three angles. What is the measure, in degrees, of Z?

Answer Key

1. C   2. D   3. C   4. D

5. C   6. A   7. C   8. D

9. B 10. A

Answer Explanations

  1. C.    Each of the four small triangles is a 45-45-90 right triangle whose hypotenuse is 2. Therefore, each leg is  The perimeter of 2 each small triangle is 2 + 2, and the sum of the perimeters is 4 times as great: 8 + 8

  2. D.    Draw a diagram and label it.

Since the area is 144, then 144 = 4x²  x² = 36  x = 6.

The width is 6, the length is 24, and the perimeter is 60.

  3. C.    The sum of the degree measures of the angles of a five-sided polygon is (5 – 2) × 180 = 3 × 180 = 540. Then: 540 = 2x + 3x + 3x + 5x + 5x = 18x.

So, x = 540 ÷ 18 = 30.

The degree measure of the smallest angle is 2x: 2 × 30 = 60.

  4. D.    Draw a diagram and label it. Since BCD is a 30-60-90 right triangle, BC is 6 (half the hypotenuse) and CD is 6 .

Then the area of rectangle ABCD is w = 6(6) = 36.

  5. C.    The perimeter of the rectangle is 2( + w) = 2(6 + 6) = 12 + 12.

  6. A.    Let x represent the side of the square. Then the dimensions of the rectangle are (x + 5) and (x – 5), and its area is (x + 5)(x – 5) = x² – 25. Since 45 is the area of the square, x² = 45, and so x² – 25 = 20.

  7. C.    Each triangle surrounding quadrilateral MNOP is a 6-8-10 right triangle. Then, each side of the quadrilateral is 10, and its perimeter is 40.

  8. D.    The area of each of the triangles is (6)(8) = 24, so together the four triangles have an area of 96. The area of the rectangle is 16 × 12 = 192. Therefore, the area of quadrilateral MNOP is 192 – 96 = 96.
NOTE: Joining the midpoints of the four sides of any quadrilateral creates a parallelogram whose area is one-half the area of the original quadrilateral.

  9. B.    Since M and N are midpoints of sides of length 2, AM, MB, AN, and ND are each equal to 1. Also, MN = , since it’s the hypotenuse of an isosceles right triangle whose legs are 1; and BD = 2, since it’s the hypotenuse of an isosceles right triangle whose legs are 2. Then, the perimeter of the shaded region is 1 +  + 1 + 2 = 2 + 3.

10. A.    The area of ABD = (2)(2) = 2, and the area of AMN = (1)(1) = 0.5. The area of the shaded region is 2 – 0.5 = 1.5.

11. (50) The sum of the degree measures of two consecutive angles of a parallelogram is 180, so

180 = (3x – 5) + (2x – 15) = 5x – 20.

So, 5x = 200  x = 40.

Since opposite angles of a parallelogram are equal, y = 3x – 5 = 115 and z = 2x – 15 = 65. Then y – z = 50.

12.    (720) Each of the 10 marked angles is an exterior angle of the pentagon. If you take one angle at each vertex, the sum of the degree measures of those five angles is 360; the sum of the degree measures of the other five is also 360: 360 + 360 = 720.

13.    (102) The area of rectangle ABCD = (x + 1)(x + 4) = x² + 5x + 4. The area of rectangle EFGH = (x + 2)(x + 3) = x² + 5x + 6, which is exactly 2 more than the area of rectangle ABCD: 100 + 2 = 102.

14.    (18) The sum of the degree measures of an interior and exterior angle is 180, so 180 = 8x + x = 9x  x = 20.

Since the sum of the degree measures of all the exterior angles of a polygon is 360, there are 360 ÷ 20 = 18 angles and, of course, 18 sides.

15.    (150) Let W, X, Y, and Z represent the degree measures of the four angles. Since

9-L Circles

A circle consists of all the points that are the same distance from one fixed point, called the center. That distance is called the radius of the circle. The figure at the right is a circle of radius 1 unit whose center is at point O. A, B, C, D, and E, which are each 1 unit from O, are all

points on circle O. The word radius is also used to represent any of the line segments joining the center and a point on the circle. The plural of radius is radii. In circle O, above, OA, OB, OC, OD, and OE are all radii. If a circle has radius r, each of the radii is r units long.

Key Fact L1

Any triangle, such as COD in the figure above, formed by connecting the endpoints of two radii is isosceles.

EXAMPLE 1

If P and Q are points on circle O, what is the value of x?

Solution. Since OP  OQ (each is a radius of the circle), POQ is isosceles. Then P and Q are congruent, so

70 + x + x = 180  2x = 110  x = 55.

A line segment, such as BE in circle O at the beginning of this section, whose endpoints are on a circle and that passes through the center is called a diameter. Since BE is made up of two radii, OB and OE, a diameter is twice as long as a radius.

Key Fact L2

If d is the diameter and r the radius of a circle, then d = 2r.

Key Fact L3

A diameter is the longest line segment that can be drawn in a circle.

The total length around a circle, from A to B to C to D to E and back to A in the circle at the beginning of this section, is called the circumference of the circle. In every circle the ratio of the circumference to the diameter is exactly the same and is denoted by the symbol  (the Greek letter pi).

Key Fact L4

For every circle:

REFERENCE FACT

The formula for the circumference of a circle is one of the facts provided in the “Reference Information” at the beginning of each math section.

Key Fact L5

The value of  is approximately 3.14.

 CALCULATOR HINT

On almost every question on the SAT that involves circles, you are expected to leave your answer in terms of , so don’t multiply by 3.14 unless you must. If you need an approximation—to test a choice, for example—then use your calculator. If you have a scientific calculator, use the  key. This not only is faster and more accurate than punching in 3.14, but also avoids careless mistakes in entering.

EXAMPLE 2

In the figure above, square ABCD is inscribed in circle O. If the area of the square is 50, what is the circumference of the circle?

(A) 

(B) 10

(C) 25

(D) 50

(E) 100

Solution. Since the area of square ABCD is 50, the length of each side is  Diagonal AC divides the square into two isosceles right triangles whose legs are  and whose hypotenuse is  But since AC is also a diameter of circle O, the circumference is d = 10 (B).

An arc consists of two points on a circle and all the points between them. If two points, such as P and Q in circle O, are the endpoints of a diameter, they divide the circle into two arcs called semicircles. On the SAT, arc AB always refers to the small arc joining A and B. To refer to the large arc going from A to B through P and Q, we would say arc APB or arc AQB.

An angle whose vertex is at the center of a circle is called a central angle.

Key Fact L6

The degree measure of a complete circle is 360.

Key Fact L7

The degree measure of an arc equals the degree measure of the central angle that intercepts it.

CAUTION: Degree measure is not a measure of length. In the circles above, arc AB and arc CD each measure 72°, even though arc CD is much longer.

How long is arc CD? Since the radius of circle P is 10, its circumference is 20 [2r = 2(10) = 20]. Since there are 360° in a circle, arc CD is  of the circumference: 

Key Fact L8

The formula for the area of a circle of radius r is A = r ².

The area of circle P in Key Fact L7 is (10)² = 100 square units.

The area of sector CPD is  of the area of the circle: (100) = 20.

REFERENCE FACT

KEY FACT L8 is one of the facts provided in the “Reference Information” at the beginning of each math section.

Key Fact L9

If an arc measures x°, the length of the arc is  and the area of the sector formed by the arc and two radii is 

Examples 3 and 4 refer to the circle below.

EXAMPLE 3

What is the area of the shaded region?

(A) 144 – 144

(B) 144 – 36

(C) 144 – 72

(D) 24 – 36

(E) 24 – 72

Solution. The area of the shaded region is equal to the area of sector COD minus the area of COD. The area of the circle is  the area of sector COD is (144) = 24. Since mO = 60, mC + mD = 120; but COD is isosceles, so C = D. Therefore, each measures 60°, and the triangle is equilateral. Finally, by KEY FACT J15, 

so the area of the shaded region is 24 – 36  (D).

EXAMPLE 4

What is the perimeter of the shaded region?

(A) 12 + 4

(B) 12 + 12

(C) 12 + 24

(D) 12 + 4

(E) 12 + 24

Solution. Since COD is equilateral, CD = 12. Since

the perimeter is 12 + 4 (A).

A line and a circle or two circles are tangent if they have only one point of intersection. A circle is inscribed in a triangle or square if it is tangent to each side. A polygon is inscribed in a circle if each vertex is on the circle.

EXAMPLE 5

A is the center of a circle whose radius is 10, and B is the center of a circle whose diameter is 10. If these two circles are tangent to one another, what is the area of the circle whose diameter is AB?

(A) 30

(B) 56.25 

(C) 100

(D) 225

(E) 400

Solution. Draw a diagram. Since the diameter of circle B is 10, its radius is 5. Then the diameter, AB, of the dotted circle is 15, its radius is 7.5, and its area is (7.5)² = 56.25 (B). (Note that you should use your calculator to square 7.5 but not to multiply by .)

Helpful Hint

On multiple-choice questions involving circles, the choices are almost always in terms of , so you shouldn’t multiply anything by 3.14.

EXAMPLE 6

In the figure above, square ABCD is inscribed in a circle whose center is O and whose radius is 4. If EO  AB at F, what is the length of EF?

(A) 2

(B) 

(C) 2 

(D) 4 – 

(E) 4 – 2

Solution. Draw diagonal AC. Then, AFO is a 45-45-90 right triangle. Since hypotenuse AO is a radius, its length is 4; and by KEY FACT J8:

EO = 4 since it is also a radius. Then

EF = EO – OF = 4 – 2 (E).

In the figure below, line  is tangent to circle O at point P.

An important theorem in geometry states that radius OP is perpendicular to .

Key Fact L10

A line tangent to a circle is perpendicular to the radius drawn to the point of contact.

EXAMPLE 7

In the figure above, AB is tangent to circle O at point P. If OB = 15 and PB = 12, what is QB?

Solution. Draw in radius OP, creating OPB. By KEY FACT L10, OP  AB, so OPB is a right triangle. Then, by the Pythagorean theorem,

Since all radii are equal, OQ = 9 and so QB = 15 – 9 = 6.

Helpful Hint

You don’t have to take the time to use the Pythagorean theorem if you recognize this as a multiple of a 3-4-5 triangle.

Exercises on Circles

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

1.   What is the circumference of a circle whose area is 100?

(A) 10

(B) 20

(C) 10

(D) 20

(E) 25

2.   What is the area of a circle whose circumference is ?

(A) 

(B) 

(C) 

(D) 2

(E) 4

3.   What is the area of a circle that is inscribed in a square of area 2?

(A) 

(B) 

(C) 

(D) 

(E) 2

4.   A square of area 2 is inscribed in a circle. What is the area of the circle?

(A) 

(B) 

(C) 

(D) 

(E) 2

Questions 5 and 6 refer to the following figure.

5.   What is the length of arc RS?

(A)   8

(B) 20

(C)   8

(D) 20

(E) 40

6.   What is the area of the shaded sector?

(A)   8

(B) 20

(C)   8

(D) 20

(E) 40

7.   In the figure above, what is the value of x?

(A) 30

(B) 36

(C) 45

(D) 54

(E) 60

8.   If A is the area and C the circumference of a circle, which of the following is an expression for A in terms of C?

(A) 

(B) 

(C) 

(D) 

(E) 

9.   What is the area of a circle whose radius is the diagonal of a square whose area is 4?

(A) 2

(B) 2

(C) 4

(D) 8

(E) 16

10. In the figure above,  is tangent to circle O at A, and OA = AB = 2. What is the area of the shaded region?

(A) 

(B) 4 – 

(C) 2 – 

(D) 2 – 

(E) 4 – 4

Grid-in Questions

11. The circumference of a circle is a units, and the area of the circle is b square units. If a = b, what is the radius of the circle?

12. A 9 × 12 rectangle is inscribed in a circle. What is the radius of the circle?

13. In the figure below, the ratio of the length of arc AB to the circumference of the circle is 2 to 15. What is the value of y?

14. If the area of the shaded region is k, what is the value of k?

15. If line  is tangent to circle O at point P, if B is a point on  such that PB = 8, and if OB = 10, what is the radius of the circle?

Answer Key

1. D   2. A   3. B   4. C

5. C   6. E   7. D   8. A

9. D 10. C

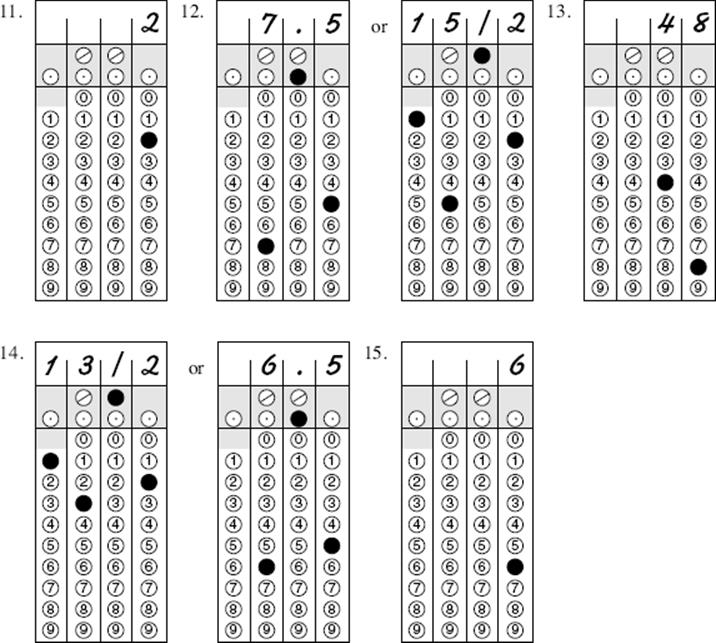
Answer Explanations

  1. C.    A = r² = 100  r² = 100  r = 10.
C = 2r = 2(10) = 20.

  2. A.    C = 2r =   2r = 1  r = .

  3. B.    Draw a diagram. Since the area of square ABCD is 2, AD = .
Then, diameter EF = 
and radius OE =  So 

  4. C.    Draw a diagram. Since the area of square ABCD is 2, AD=  Then diagonal BD = × = 2. But BD is also a diameter of the circle, so the diameter is 2 and the radius is 1. Therefore, the area is (1)² = .

  5. C.     The length of arc   [Note that, instead of reducing  you should use your calculator and divide: 144 ÷ 360 = 0.4, and (0.4)(20) = 8.]

  6. E.    The area of the shaded sector is

  7. D.    The triangle is isosceles, so the third (unmarked) angle is also x:

  8. A.    

  9. D.    If the area of the square is 4, each side is 2, and the length of a diagonal is 2  .
The area of a circle whose radius is 2  is (2  )² = 8.

10. C.    Since  is tangent to circle O at A, OA   and OAB is an isosceles right triangle. Then m O = 45. 
The area of the shaded region is the area of OAB minus the area of sector OAC.
The area of OAB is (2)(2) = 2. Since the area of the circle is (2²) = 4, the area of sector OAC is  of 4, or .
Finally, the area of the shaded region is 2 – .

11. (2)     Since a = b, then C = a = b = A, so 2r = r²  2r = r²  r = 2.

12.     Draw a diagram. By the Pythagorean 7 5 theorem (or by recognizing a 3x-4x-5x triangle with x = 3), the length of diagonal AC is 15. But AC is also a diameter of the circle, so the diameter is 15 and the radius is 7.5 or 

13. (48)    Since arc AB is  of the circumference, y is  × 360 = 48.

14.      The area of the circle is 9; and since the white region is  of the circle, the shaded region is  of it: 

15. (6) Draw a diagram and label it.

Since radius OP is perpendicular to , OPB is a right triangle.
By the Pythagorean theorem, OP² + 8² = 10²  OP² + 64 = 100.
So, OP² = 36  OP = 6.

(Of course, you should save time by recognizing a 6-8-10 right triangle.)

9-M Solid Geometry

There is very little solid geometry on the SAT. Basically, all you need to know are the formulas for the volumes and surface areas of rectangular solids (including cubes) and cylinders.

A rectangular solid or box is a solid formed by six rectangles, called faces. The sides of the rectangles are called edges. As shown in the diagram that follows, the edges are the lengthwidth, and height.

A cube is a rectangular solid in which the length, width, and height are equal, so that all the edges are the same length.

The volume of a solid, which is the amount of space it occupies, is measured in cubic units. One cubic unit is the amount of space occupied by a cube all of whose edges are 1 unit long. In the figure above, if the length of each edge of the cube is 1 inch, the area of each face is 1 square inch, and the volume of the cube is 1 cubic inch.

Key Fact M1

The formula for the volume of a rectangular solid is V = wh.

In a cube, all the edges are equal. Therefore, if e is the length of an edge, the formula for the volume is V = e³.

REFERENCE FACT

KEY FACT M1 is one of the facts provided in the “Reference Information” at the beginning of each math section.

EXAMPLE 1

The base of a rectangular tank is 2 feet wide and 4 feet long; the height of the tank is 20 inches. If water is pouring into the tank at the rate of 2 cubic inches per second, how many hours will be required to fill the tank?

Solution. Draw a diagram. Change all the units to inches (2 feet = 24 inches and 4 feet = 48 inches). Then the volume of the tank is 24 × 48 × 20 = 23,040 cubic inches. At 2 cubic inches per second:

      

The surface area of a rectangular solid is the sum of the areas of the six faces. Since the top and bottom faces are equal, the front and back faces are equal, and the left and right faces are equal, you can calculate the area of one face from each pair and then double the sum. In a cube, each of the six faces has the same area.

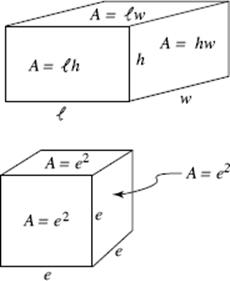
Key Fact M2

The formula for the surface area of a rectangular solid is . The formula for the surface area of a cube is A = 6e².

EXAMPLE 2

The volume of a cube is v cubic yards, and its surface area is a square feet. If v = a, what is the length, in inches, of each edge?

Solution. Draw a diagram. If e is the length of the edge in yards, then 3e is the length in feet, and 36e is the length in inches.

Therefore, v = e³ and a = 6(3e)² = 6(9e²) = 54e².

Since v = a, e³ = 54e²  e = 54; the length of each edge is 36(54) = 1944 inches.

A diagonal of a box is a line segment joining a vertex on the top of the box to the opposite vertex on the bottom. A box has four diagonals, all the same length. In the box below they are line segments AG, BH, CE, and DF.

Key Fact M3

A diagonal of a box is the longest line segment that can be drawn between two points on the box.

Key Fact M4

If the dimensions of a box are , w, and h, and if d is the length of a diagonal, then d² =  ² + w² + h².

For example, in the box below:

d² = 3² + 4² + 12² = 9 + 16 + 144 = 169  d = 13.

This formula is really just an extended Pythagorean theorem. EG is the diagonal of rectangular base EFGH. Since the sides of the base are 3 and 4, EG is 5. Now, CGE is a right triangle whose legs are 12 and 5, so diagonal CE is 13. (The only reason not to use the Pythagorean theorem is that these triangles are so familiar.)

EXAMPLE 3

What is the length of a diagonal of a cube whose sides are 1?

Solution. Use the formula:

Without the formula you would draw a diagram and label it. Since the base is a 1 × 1 square, its diagonal is . Then the diagonal of the cube is the hypotenuse of a right triangle whose legs are 1 and , so

A cylinder is similar to a rectangular solid except that the base is a circle instead of a rectangle. The volume of a cylinder is the area of its circular base (r²) times its height (h). The surface area of a cylinder depends on whether you are envisioning a tube, such as a straw, without a top or bottom, or a can, which has both a top and a bottom.

Key Fact M5

• The volume, V, of a cylinder whose circular base has radius r and whose height is h is the area of the base times the height:

V = r²h.

• The surface area, A, of the side of the cylinder is the circumference of the circular base times the height:

A = 2rh.

REFERENCE FACT

The formula for the volume of a cylinder is one of the facts provided in the “Reference Information” at the beginning of each math section.

EXAMPLE 4

The volume of a cube and the volume of a cylinder are equal. If the edge of the cube and the radius of the cylinder are each 6, which of the following is the best approximation of the height of the cube?

(A) 1

(B) 2

(C) 3

(D) 6

(E) 12

Solution. The volume of the cube is 6³ = 216. The volume of the cylinder is (6²)h = 36h.

Then

Since  is approximately 3, h is approximately 2 (B).

You now know the only formulas you will need. Any other solid geometry questions that may appear on the SAT will require you to visualize a situation and reason it out, rather than to apply a formula.

EXAMPLE 5

How many small blocks are needed to construct the tower in the figure above?

Solution. You need to “see” the answer. The top level consists of 1 block, the second and third levels consist of 9 blocks each, and the bottom layer consists of 25 blocks. The total is 1 + 9 + 9 + 25 = 44.

Exercises on Solid Geometry

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

1.   What is the volume of a cube whose surface area is 150?

(A)        25

(B)      100

(C)      125

(D)    1000

(E) 15,625

2.   What is the surface area of a cube whose volume is 64?

(A)   16

(B)   64

(C)   96

(D) 128

(E) 384

3.   A solid metal cube of side 3 inches is placed in a rectangular tank whose length, width, and height are 3, 4, and 5 inches, respectively. What is the volume, in cubic units, of water that the tank can now hold?

(A) 20

(B) 27

(C) 33

(D) 48

(E) 60

4.   The height, h, of a cylinder is equal to the edge of a cube. If the cylinder and the cube have the same volume, what is the radius of the cylinder?

(A) 

(B) 

(C) 

(D) 

(E) 

5.   If the height of a cylinder is 4 times its circumference, what is the volume of the cylinder in terms of its circumference, C?

(A) 

(B) 

(C) 

(D) 

(E) 

Grid-in Questions

6.   The sum of the lengths of all the edges of a cube is 6 centimeters. What is the volume, in cubic centimeters, of the cube?

7.   A 5-foot-long cylindrical pipe has an inner diameter of 6 feet and an outer diameter of 8 feet. If the total surface area (inside and out, including the ends) is k, what is the value of k?

8.   What is the number of cubic inches in 1 cubic foot?

9.   A rectangular tank has a base that is 10 centimeters by 5 centimeters and a height of 20 centimeters. If the tank is half full of water, by how many centimeters will the water level rise if 325 cubic centimeters are poured into the tank?

10. Three identical balls fit snugly into a cylindrical can: the radius of the spheres equals the radius of the can, and the balls just touch the bottom and the top of the can. If the formula for the volume of a sphere is  what fraction of the volume of the can is taken up by the balls?

Answer Key

1. C   2. C

3. C   4. A

5. A

Answer Explanations

  1. C.    Since the surface area is 150, each of the six faces of the cube is a square whose area is 150 ÷ 6 = 25. Then, each edge is 5, and the volume is 5³ = 125.

  2. C.    Since the volume of the cube is 64, then e³ = 64  e = 4. The surface area is 6e² = 6 × 16 = 96.

  3. C.    The volume of the tank is 3 × 4 × 5 = 60 cubic units, but the solid cube is taking up 3³ = 27 cubic units. Therefore, the tank can hold 60 – 27 = 33 cubic units of water.

  4. A.    Since the volumes are equal, r²h = e³ = h³. Therefore, 

  5. A.    Since V = r²h, you need to express r and h in terms of C. It is given that h = 4C; and since C = 2r, then  Therefore,

  6. A.     Since a cube has 12 edges:

Therefore: 

  7. (84)    Draw a diagram and label it. Since the surface of a cylinder is given by A = 2rh, the area of the exterior is 2(4)(5) = 40, and the area of the interior is 2(3)(5) = 30. The area of each shaded end is the area of the outer circle minus the area of the inner circle: 16 – 9 = 7, so

total surface area = 40 + 30 + 7 + 7 = 84  k = 84.

  8. (1728)     The volume of a cube whose edges are 1 foot can be expressed in either of two ways:

(1 foot)³ = 1 cubic foot or
(12 inches)³ = 1728 cubic inches.

  9. (6.5)     Draw a diagram. Since the area of the base is 5 × 10 = 50 square centimeters, each 1 centimeter of depth has a volume of 50 cubic centimeters. Therefore, 325 cubic centimeters will raise the water level 325 ÷ 50 = 6.5 centimeters. (Note that the fact that the tank was half full was not used, except to be sure that the tank didn’t overflow. Since the tank was half full, the water was 10 centimeters deep, and the water level could rise by 6.5 centimeters. Had the tank been three-fourths full, the water would have been 15 centimeters deep, and the extra water would have caused the level to rise 5 centimeters, filling the tank; the rest of the water would have spilled out.)

10.     To avoid using r, assume that the radii of the spheres and the can are 1. Then the volume of each ball is  and the total volume of the three balls is  Since the volume of the can is (1)²(6) = 6, the balls take up of  the can. Grid in  or .666 or .667.

9-N Coordinate Geometry

The coordinate plane is formed by two perpendicular number lines called the x-axis and y-axis, which intersect at the origin. The axes divide the plane into four quadrants, labeled, in counterclockwise order, I, II, III, and IV.

Each point in the plane is assigned two numbers, an x-coordinate and a y-coordinate, which are written as an ordered pair, (x, y).

• Points to the right of the y-axis have positive x-coordinates, and those to the left have negative x-coordinates.

• Points above the x-axis have positive y-coordinates, and those below it have negative y-coordinates.

• If a point is on the x-axis, its y-coordinate is 0.

• If a point is on the y-axis, its x-coordinate is 0.

For example, point A in the figure below is labeled (2, 3), since it is 2 units to the right of the y-axis and 3 units above the x-axis. Similarly, point B(–3, –5) is in Quadrant III, 3 units to the left of the y-axis and 5 units below the x-axis.

EXAMPLE 1

In the figure above, all of the following are equal EXCEPT

(A) ab

(B) ac

(C) ad

(D) bc

(E) bd

Solution. Since (a, b) lies on the x-axis, b = 0. Since (c, d) lies on the y-axis, c = 0. Each of the choices is equal to 0 except ad (C).

EXAMPLE 2

In the figure above, which of the following must be true?

  I. rs < 0

 II. r < s

III. r + s = 0

(A) None

(B) I only

(C) II only

(D) I and II only

(E) I, II, and III

Solution. Since (r, s) is in Quadrant II, r is negative and s is positive. Then rs < 0 (I is true) and r < s (II is true). Although r + s could be equal to 0, it does not have to equal 0 (III is false). Only I and II must be true (D).

Often a question requires you to calculate the distance between two points. This task is easiest when the points lie on the same horizontal or vertical line.

Key Fact N1

• All the points on a horizontal line have the same y-coordinate. To find the distance between them, subtract their x-coordinates.

• All the points on a vertical line have the same x-coordinate. To find the distance between them, subtract their y-coordinates.

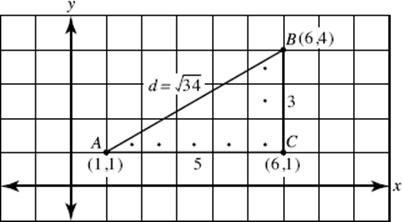
In the graph, the distance from A to C is 6 – 1 = 5. The distance from B to C is 4 – 1 = 3.

It is a little harder, but not much, to find the distance between two points that are not on the same horizontal or vertical line; just use the Pythagorean theorem. For example, in the preceding graph, if d represents the distance from Ato B,

Key Fact N2

The distance, d, between two points, A(x₁, y₁) and B(x₂, y₂), can be calculated using the distance formula:

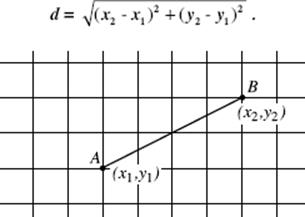
The distance formula is nothing more than the Pythagorean theorem, so you never need to use it. You can always create a right triangle by drawing a horizontal line through one of the points and a vertical line through the other, and then use the Pythagorean theorem. For example, to find the distance between A(1, 1) and B(5, 4), create a right triangle by drawing a horizonal line through A and a vertical line through B.

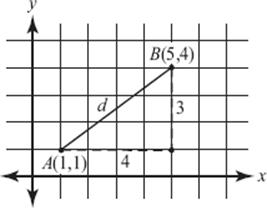
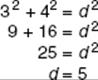
Examples 3 and 4 refer to the triangle in the following figure.

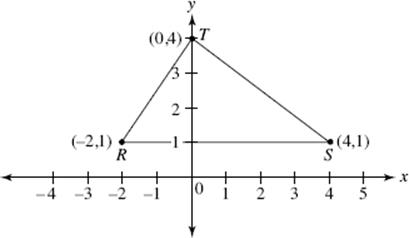
EXAMPLE 3

What is the area of RST?

(A) 6

(B) 9

(C) 12

(D) 15

(E) 18

Solution. R(–2, 1) and S(4, 1) lie on the same horizontal line, so RS = 4 – (–2) = 6. Let that be the base of the triangle. Then the height is the distance along the vertical line from T to RS:

4 – 1 = 3. The area is (6)(3) = 9 (B).

EXAMPLE 4

What is the perimeter of RST?

(A) 13

(B) 14

(C) 16

(D) 11 +

(E) 11 +

Solution. The perimeter is RS + ST + RT. From the solution to Example 3, you know that RS = 6. Also, ST = 5, since it is the hypotenuse of a 3-4-5 right triangle. To calculate RT, use either the distance formula:

or the Pythagorean theorem:

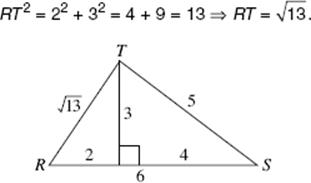
Then the perimeter is 

Key Fact N3

If P (x₁, y₁) and Q (x₂, y₂) are any two points, then the midpoint, M, of segment PQ is the point whose coordinates are 

EXAMPLE 5

A (2, –3) and B (8, 5) are the endpoints of a diameter of a circle. What are the coordinates of the center of the circle?

(A) (3, 1)

(B) (3, 4)

(C) (5, 1)

(D) (5, 4)

(E) (10, 2)

Solution. The center of a circle is the midpoint of any diameter. Therefore, the coordinates are 

The slope of a line is a number that indicates how steep the line is.

Key Fact N4

• Vertical lines do not have slopes.

• To find the slope of any other line, proceed as follows:

1. Choose any two points, A (x₁ , y₁) and B (x₂, y₂), on the line.

2. Take the differences of the y-coordinates, y₂ – y₁, and the x-coordinates, x₂ – x₁.

3. Divide: slope = 

We will illustrate each part of KEY FACT N5 by using the slope formula to calculate the slopes of RS, RT, and ST from Example 3: R(–2, 1), S(4, 1), T(0, 4).

Key Fact N5

• The slope of any horizontal line is 0:

• The slope of any line that goes up as you move from left to right is positive:

• The slope of any line that goes down as you move from left to right is negative:

EXAMPLE 6

In the figure above, which line has the greatest slope?

(A) 

(B) m

(C) n

(D) p

(E) q

Solution. Since the slope of line  is 0 and the slopes of lines n and q are negative, eliminate choices A, C, and E. Lines m and p have positive slopes, but line p is steeper. (D)

The next key fact concerns the relationships between the slopes of parallel and perpendicular lines.

Key Fact N6

• If two nonvertical lines are parallel, their slopes are equal.

• If two nonvertical lines are perpendicular, the product of their slopes is –1.

If the product of two numbers, r and s, is –1, then

Therefore, another way to express the second part of KEY FACT N6 is to say that, if two nonvertical lines are perpendicular, the slope of one is the negative reciprocal of the slope of the other.

EXAMPLE 7

In the figure above, line  passes through points (1, 2) and (3, 5). Line m (not shown) is perpendicular to . What is the slope of line m?

(A) 

(B) 

(C) 0

(D) 

(E) 

Solution. First use the slope formula to calculate the slope of line 

Then the slope of line m is the negative reciprocal of  which is 

Note that you can see from the diagram in Example 7 that the slope of  is positive. If you sketch any line perpendicular to , you can see that its slope is negative. So immediately you know the answer must be A or B.

Every line that is drawn in the coordinate plane has an equation. All the points on a horizontal line have the same y-coordinate. For example, in the following figure, horizontal line  passes through (–3, 3), (0, 3), (2, 3), (5, 3), and (10, 3).

The equation of line  is y = 3.

Similarly, every point on vertical line m has an x-coordinate equal to 5, and the equation of m is x = 5.

Every other line in the coordinate plane has an equation that can be written in the form y = mx + b, where m is the slope of the line and b is the y-intercept—the y-coordinate of the point where the line crosses the y-axis. These facts are summarized in KEY FACT N7.

Key Fact N7

• For any real number a: x = a is the equation of the vertical line that crosses the x-axis at (a, 0).

• For any real number b: y = b is the equation of the horizontal line that crosses the y-axis at (0, b).

• For any real numbers b and m: y = mx + b is the equation of the line that crosses the y-axis at (0, b) and whose slope is m.

On the SAT, you won’t have to graph a line, but you may have to recognize the graph of a line. In a multiple-choice question, you may be given the graph of a line and asked which of the five choices is the equation of that line; or you may be given the equation of a line and asked which of the five choices is the correct graph.

EXAMPLE 8

Which of the following is the equation of the line in the figure above?

(A) y = 2x + 4

(B) y = x + 4

(C) y = 2x – 2

(D) y = x – 4

(E) y = 4x + 2

There are two different ways to handle this question.

Solution 1. Since the line is neither horizontal nor vertical, its equation has the form y = mx + b. Since the line crosses the y-axis at 4, b = 4. Also, since the line passes through (–2, 0) and (0, 4), its slope is 

So m = 2, and the equation is y = 2 x + 4 (A).

Solution 2. Test some points. Since the line passes through (0, 4), y = 4 when x = 0. Plug in 0 for x in the five choices; only in A and B does y equal 4. The line also passes through (–2, 0), so when x = –2, y = 0.

Replace x by –2 in choices A and B.

• 2 (–2) + 4 = –4 + 4 = 0, so A works.

• (–2) + 4 = –1 + 4 = 3, so B does not work.

EXAMPLE 9

Which of the following is the graph of the line whose equation is 3y = 2x + 6?

Solution 1. Express 3y = 2x + 6 in standard form by dividing each term by . From this equation you see that the y-intercept is 2. Eliminate choices A, B, and E. Since the slope  is positive, eliminate C. The answer must be D.

Solution 2. Test some points.

• When x = 0, 3y = 2(0) + 6 = 6  y = 2, so (0, 2) is a point on the graph.

• When x = 3, 3y = 2(3) + 6 = 12  y = 4, so (3, 4) is on the graph.

Only choice D passes through both (0, 2) and (3, 4).

Exercises on Coordinate Geometry

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

1.   If A(–1, 1) and B(3, –1) are the endpoints of one side of square ABCD, what is the area of the square?

(A) 12

(B) 16

(C) 20

(D) 25

(E) 36

2.   If P(2, 1) and Q(8, 1) are two of the vertices of a rectangle, which of the following cannot be another of the vertices?

(A) (2, 8)

(B) (8, 2)

(C) (2, –8)

(D) (–2, 8)

(E) (8, 8)

3.   A circle whose center is at (6,8) passes through the origin. Which of the following points is NOT on the circle?

(A) (12, 0)

(B) (6, –2)

(C) (16, 8)

(D) (–2, 12)

(E) (–4, 8)

4.   What is the slope of the line that passes through 

(A) 0

(B) 

(C) 

(D) 

(E) Undefined

5.   If c  0 and the slope of the line passing through (–c, c) and (3c, a) is 1, which of the following is an expression for a in terms of c?

(A) –3c

(B) 

(C) 2c

(D) 3c

(E) 5c

6.   What is the slope of the line that passes through (3, 2) and is parallel to the line that passes through (–2, 3) and (2, –3)?

(A) 

(B) 

(C)    

(D)    1

(E)    

7.   What is the slope of the line that passes through (3, 2) and is perpendicular to the line that passes through (–2, 3) and (2, –3)?

(A) 

(B) 

(C)    

(D)    1

(E)    

8.   What is the equation of the line that passes through (4, –4) and (4, 4)?

(A) x = 4

(B) y = 4

(C) y = 4x

(D) y = 4x + 4

(E) y = 4x – 4

9.   Line  is tangent to a circle whose center is at (3, 2). If the point of tangency is (6, 6), what is the slope of line ?

(A) 

(B) 

(C)    0

(D)    

(E)    

10. What is the equation of the line that crosses the y-axis at (0, 5) and crosses the x-axis at (5, 0)?

(A) x = 5

(B) y = 5

(C) y = x + 5

(D) y = x – 5

(E) y = –x + 5

Grid-in Questions

11. If the coordinates of RST are R(0, 0), S(7, 0), and T(2, 5), what is the sum of the slopes of the three sides of the triangle?

12. If the area of circle O below is k, what is the value of k?

Questions 13 and 14 concern parallelogram JKLM, whose coordinates are J(–5, 2), K(–2, 6), L(5, 6), M(2, 2).

13. What is the area of parallelogram JKLM?

14. What is the perimeter of parallelogram JKLM?

15. What is the area of quadrilateral ABCD?

Answer Key

1. C   2. D   3. D   4. A

5. E   6. A   7. C   8. A

9. B 10. E

Answer Explanations

  1. C.    The area of square ABCD is s², where s = AB. To calculate s, use the distance formula:

Then s² = 20.

  2. D.    Draw a diagram. Any point whose x-coordinate is 2 or 8 could be another vertex. Of the choices, only (–2, 8) is not possible.

  3. D.    Draw a diagram. The radius of the circle is 10 (since it’s the hypotenuse of a 6-8-10 right triangle). Which of the choices is (are) 10 units from (6, 8)?

• First, check the easy ones; E: (–4, 8) and C: (16, 8) are 10 units to the left and right of (6, 8), and B: (6, –2) is 10 units below.

• Check A: (12, 0), which works, and D: (–2, 12), which doesn’t.

The answer is D.

  4. A.    The formula for the slope is  but before using it, look at the question again. Since the y-coordinates are equal, the numerator, and thus the fraction, equals 0.

  5. E.    The slope is equal to

  6. A.    Use TACTIC 1: draw a diagram. Quickly sketch the line through (–2, 3) and (2, –3) and the line parallel to it that goes through (3, 2).

Clearly, the slopes of both lines are negative. The answer must be A or B. By KEY FACT N4, the slope of the line through (–2, 3) and (2, –3) is

By KEY FACT N6, nonvertical parallel lines have equal slopes, so the answer is  Note 2 that it is irrelevant that the second line passes through (3, 2).

  7. C.    By KEY FACT N4, the slope of the line through (–2, 3) and (2, –3) is

By KEY FACT N6, if two nonvertical lines are perpendicular, the product of their slopes is –1. Then, if m is the slope of the perpendicular line,

As in Exercise 6, it is irrelevant that the line passes through (3, 2).

  8. A.    A quick sketch shows that the line that passes through (4, –4) and (4, 4) is vertical. Then, by KEY FACT N7, its equation is x = 4.

  9. B.    Draw a rough sketch.

Line segment OP, joining (3, 2) and (6, –6) is a radius and so, by KEY FACT L10, is perpendicular to line . The slope of OP is  Therefore, the slope of  is 

10. E.    Since the line is neither horizontal nor vertical, its equation has the form y = mx + b. Since it crosses the y-axis at (0, 5), b = 5. Since it passes through (0, 5) and (5, 0), its slope is  and its equation is y = –1x + 5 or y = –x + 5.

11. (1.5)    Sketch the triangle, and then calculate the slopes. Since RS is horizontal, its slope is 0.

The slope of 

The slope of 

Now add: 0 + 2.5 + (–1) = 1.5.

12. (18)    Since the line segment joining (3, 3) and (0, 0) is a radius of the circle, the radius equals 3.

Therefore,

     area = 

Here is the diagram for solutions 13 and 14.

13. (28)    The base is 7, and the height is 4. The area is 7 × 4 = 28.

14. (24)    Sides JM and KL are each 7. Also, sides JK and LM are each the hypotenuse of a 3-4-5 right triangle, and so they are 5. The perimeter is 2(7 + 5) = 24.

15.     Draw in line segment BE, dividing quadrilateral ABCD into rectangle ABED and BEC. The area of the rectangle is 4 × 7 = 28, and the area of the triangle is (7)(3) = 10.5. The total area is 38.5 or 

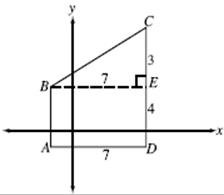
MISCELLANEOUS TOPICS

9-O Counting and Probability

Some questions on the SAT begin, “How many … .” In these problems you are being asked to count something: how many apples can Maria buy, how many dollars did Jose spend, how many pages did Elizabeth read, how many numbers satisfy a certain property, or how many ways are there to complete a particular task. Sometimes these problems can be handled by simple arithmetic. Other times it helps to use TACTIC 14 and systematically make a list. Occasionally it helps to know the counting principle and other strategies that will be reviewed in this section.

Counting

USING ARITHMETIC TO COUNT

Examples 1–3 require only arithmetic. Be careful, though; they are not the same.

EXAMPLE 1

John bought some apples. If he entered the store with $113 and left with $109, how much did the apples cost?

EXAMPLE 2

Kim was selling tickets for the school play. One day she sold tickets numbered 109 through 113. How many tickets did she sell that day?

EXAMPLE 3

John is the 109th person in a line, and Kim is the 113th person. How many people are there between John and Kim?

Solutions 1–3. It may seem that each of these examples requires a simple subtraction: 113 – 109 = 4. In Example 1, John did spend $4 on apples. In Example 2, however, Kim sold 5 tickets; and in Example 3, only 3 people are on line between John and Kim! Assume that John went into the store with 113 one-dollar bills, numbered 1 through 113; he spent the 4 dollars numbered 113, 112, 111, and 110, and still had the dollars numbered 1 through 109; Kim sold the 5 tickets numbered 109, 110, 111, 112, and 113; and between John and Kim the 110th, 111th, and 112th persons—3 people—were on line.

• In Example 1, you just need to subtract: 113 – 109 = 4.

• In Example 2, you need to subtract and then add 1: 113 – 109 + 1 = 4 + 1 = 5.

• In Example 3, you need to subtract and then subtract 1 more: 113 – 109 – 1 = 3.

Although Example 1 is too easy for the SAT, questions such as Examples 2 and 3 appear frequently, because they’re not as obvious and they require that little extra thought. When do you have to add or subtract 1?

The issue is whether or not the first and last numbers are included. In Example 1, John spent dollar number 113, but he still had dollar 109 when he left the store. In Example 2, Kim sold both ticket number 109 and ticket 113. In Example 3, neither Kim (the 113th person) nor John (the 109th person) should be counted.

Key Fact O1

To count how many integers there are between two integers, follow these rules:

• If exactly one of the endpoints is included: subtract.

• If both endpoints are included: subtract and then add 1.

• If neither endpoint is included: subtract and then subtract 1 more.

EXAMPLE 4

From 1:09 to 1:13, Elaine read pages 109 through 113 in her English book. What was her rate of reading, in pages per minute?

(A) 

(B) 

(C) 

(D) 0

(E) 

Solution. Since Elaine read both pages 109 and 113, she read 113 – 109 + 1 = 5 pages. She started reading during the minute that started at 1:09 (and ended at 1:10). Since she stopped reading at 1:13, she did not read during the minute that began at 1:13 (and ended at 1:14), so she read for 1:13 – 1:09 = 4 minutes. She read at the rate of  pages per minute (E).

SYSTEMATICALLY MAKING A LIST

When the numbers in a problem are small, it is often better to systematically list all of the possibilities than to risk making an error in arithmetic. In Example 4, rather than even thinking about whether or not to add 1 or subtract 1 after subtracting the numbers of pages, you could have just quickly jotted down the pages Elaine read (109, 110, 111, 112, 113), and then counted them.

EXAMPLE 5

Blair has 4 paintings in the basement. She is going to bring up 2 of them and hang 1 in her den and 1 in her bedroom. In how many ways can she choose which paintings go in each room?

(A)   4

(B)   6

(C) 12

(D) 16

(E) 24

Solution. Label the paintings 1, 2, 3, and 4, write B for bedroom and D for den, and make a list.

There are 12 ways to choose (C).

For additional examples of systematically making lists, see TACTIC 14 in Chapter 8.

In Example 5, making a list was feasible, but if Blair had 10 paintings and needed to hang 4 of them, it would be impossible to list all the different ways of hanging them. In such cases you need the counting principle.

USING THE COUNTING PRINCIPLE

Key Fact O2

If two jobs need to be completed and there are m ways to do the first job and n ways to do the second job, then there are m × n ways to do one job followed by the other. This principle can be extended to any number of jobs.

In Example 5, the first job was to pick 1 of the 4 paintings and hang it in the bedroom. That could be done in 4 ways. The second job was to pick a second painting to hang in the den. That job could be accomplished by choosing any of the remaining 3 paintings. There are 4 × 3 = 12 ways to hang the 2 paintings.

Now, assume there are 10 paintings to be hung in 4 rooms. The first job is to choose 1 of the 10 paintings for the bedroom. The second job is to choose 1 of the 9 remaining paintings to hang in the den. The third job is to choose 1 of the 8 remaining paintings for, say, the living room. Finally, the fourth job is to pick 1 of the 7 remaining paintings for the dining room. These 4 jobs can be completed in 10 × 9 × 8 × 7 = 5040 ways.

EXAMPLE 6

How many integers are there between 100 and 1000, all of whose digits are odd?

Solution. You’re looking for three-digit numbers, such as 135, 711, 353, and 999, in which all three digits are odd. Note that you are not required to use three different digits. Although you certainly wouldn’t want to list all of the possibilities, you could count them by listing some of them and seeing whether a pattern develops. In the 100’s there are 5 numbers that begin with 11: 111, 113, 115, 117, 119. Similarly, there are 5 numbers that begin with 13: 131, 133, 135, 137, 139; 5 numbers that begin with 15, 5 that begin with 17, and 5 that begin with 19, for a total of 5 × 5 = 25 in the 100’s. In the same way there are 25 in the 300’s, 25 in the 500’s, 25 in the 700’s, and 25 in the 900’s, for a grand total of 5 × 25 = 125. You can actually do this calculation in less time than it takes to read this paragraph.

The best way to solve Example 6, however, is to use the counting principle. Think of writing a three-digit number as three jobs that need to be done. The first job is to select one of the five odd digits and use it as the digit in the hundreds place. The second job is to select one of the five odd digits to be the digit that goes in the tens place. Finally, the third job is to select one of the five odd digits to be the digit in the units place. Each of these jobs can be done in 5 ways, so the total number of ways is 5 × 5 × 5 = 125.

COMBINATIONS AND PERMUTATIONS

Some students, by the time they take the SAT, have learned in a math class about combinations and permutations; as a result, they try to use the formulas for them on the SAT. The problem is that there has never been a single question on any SAT that requires you to know or use those formulas, and very few SATs have even one question on which you could even use those formulas. The occasional question on which you could use one of the formulas can always be solved as quickly, or even more quickly, without them.

For example, Example 6—How many integers are there between 100 and 1000, all of whose digits are odd?—could not be answered using the formula for permutations. That question should be answered using the counting principle: 5 × 5 × 5 = 125. Consider now a slight variation of Example 6: How many integers are there between 100 and 1000, all of whose digits are different odd integers? Here, because the digits have to be different, we can consider each number as a permutation of the five numbers 1, 3, 5, 7, and 9, taken three at a time. On any scientific or graphing calculator we could enter 5, then _nP_r, the button for permutations, then 3, and finally the “enter” or “equals” button. That would evaluate ₅P₃, the number of permutations of 5 things taken 3 at a time, which is equal to 60. The better thing to do would be to again use the counting principle: 5 × 4 × 3 = 60. That is just as fast, and you don’t have to worry about whether or not the formula for permutations will work; you can always use the counting principle.

Consider the following question: From a group of 4 students, in how many ways can 2 of them be chosen to attend a conference? This question can be answered by evaluating ₄C₂ on a calculator. Enter 4, then _nC_r, the button for combinations, then 2, and finally the “enter” or “equals” button. The answer is 6. You could also think of the students as A, B, C, and D, and in about the same amount of time write AB, AC, AD, BC, BD, CD and see that the answer is 6. Or you could use the counting principle: there are 4 ways to choose the first student and 3 ways to choose the second one, so it seems as if there are 4 × 3 = 12 ways; however, since each pair of students has been counted twice (AB and BA, for example), you need to divide 12 by 2 to get 6.

The bottom line is this. On any question on the SAT, you may use anything you know. Just because questions about 30-60-90 right triangles can be answered using trigonometry, doesn’t mean they should be. You never need to use the formulas for combinations and permutations. If you don’t know them, you certainly shouldn’t learn them for the SAT; if you do know them and are sure you know when they can be used and when they can’t, and you won’t ever use _nC_r instead of _nP_r (or vice versa), then you may use them if you choose to. Of course, if you do, you should never actually use the formulas; you should always just use the appropriate buttons on your calculator.

USING VENN DIAGRAMS

A Venn diagram is a figure with two or three over lapping circles, usually enclosed in a rectangle, that is used to solve certain counting problems. To illustrate, assume that a school has 100 seniors. The following Venn diagram, which divides the rectangle into four regions, shows the distribution of those students in the band and the orchestra.

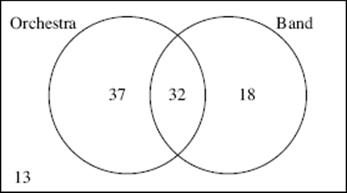
The 32 written in the part of the diagram where the two circles overlap represents the 32 seniors who are in both band and orchestra. The 18 written in the circle on the right represents the 18 seniors who are in the band but not in the orchestra, while the 37 written in the left circle represents the 37 seniors who are in the orchestra but not in the band. Finally, the 13 written in the rectangle outside the circles represents the 13 seniors who are in neither band nor orchestra. The numbers in all four regions must add up to the total number of seniors: 32 + 18 + 37 + 13 = 100.

Note that there are 50 seniors in the band—32 who are also in the orchestra and 18 who are not in the orchestra. Similarly, there are 32 + 37 = 69 seniors in the orchestra. Be careful: the 50 names on the band roster and the 69 names on the orchestra roster add up to 119 names—more than the number of seniors. The reason is that 32 names are on both lists and so have been counted twice. The number of seniors who are in band or orchestra is only 119 – 32 = 87. Those 87, together with the 13 who are in neither band nor orchestra, make up the total of 100.

Although no problem on an SAT requires the use of a Venn diagram, occasionally there will be a problem that you will be able to solve more easily if you draw a Venn diagram, as in Example 7.

EXAMPLE 7

Of the 410 students at Kennedy High School, 240 study Spanish and 180 study French. If 25 students study neither language, how many students study both?

Solution. Draw a Venn diagram. Let x represent the number of students who study both languages, and write x in the part of the diagram where the two circles overlap.

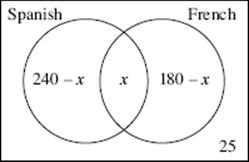
Then the number who study only Spanish is 240 – x, and the number who study only French is 180 – x. The number who study at least one of the languages is 410 – 25 = 385, so

385 = (240 – x) + x + (180 – x) = 420 – x.

So, x = 420 – 385 = 35 who study both.

Probability

The probability that an event will occur is a number between 0 and 1, usually written as a fraction, that indicates how likely it is that the event will happen. For example, for the spinner at the right, there are 4 possible outcomes: it is equally likely that the spinner will stop in any of the four regions. There is 1 chance in 4 that it will stop in the region marked 2, so we say that the probability of spinning a 2 is one-fourth and write  Since 2 is the only even number on the spinner, we could also say  Also, there are 3 chances in 4 that the spinner will land in a region with an odd number in it, so 

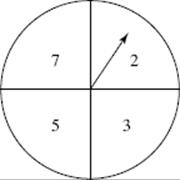
Key Fact O3

If E is any event, the probability that E will occur is given by

assuming that all of the possible outcomes are equally likely.

In the preceding example, each of the four regions is the same size, so it is equally likely that the spinner will land on the 2, 3, 5, or 7. Therefore:

Note that the probability of not getting an odd number is 1 minus the probability of getting an odd number:

Let’s look at some other probabilities associated with spinning this spinner once:

NOTE

Although probabilities are defined as fractions, they can also be written as decimals or percents.

Key Fact O4

Let E be an event, and let P(E) be the probability that it will occur.

• If E is impossible (such as getting a number greater than 10 in the spinner example), P(E) = 0.

• If it is certain that E will occur (such as getting a prime number in the spinner example), P(E) = 1.

• In all cases, 

• The probability that event E will not occur is 1 – P(E).

• If two or more events constitute all the outcomes, the sum of their probabilities is 1.

• The more likely it is that an event will occur, the higher (the closer to 1) its probability is; the less likely it is that an event will occur, the lower (the closer to 0) its probability is.

Even though probability is defined as a fraction, probabilities can also be written as decimals or percents.

Instead of writing P(E) = , you can write

P(E) = .50 or P(E) = 50%.

REMEMBER

The answer to a probability problem can never be negative and can never be greater than 1.

EXAMPLE 8

In 2003, Thanksgiving was on Thursday, November 27, and there are 30 days in November. If one day in November 2003 was chosen at random for a concert, what is the probability that the concert was on a weekend (Saturday or Sunday)?

There are two ways to answer this: either quickly draw a calendar, or reason out the solution.

Solution 1. Make a blank calendar and put 27 in the Thursday column:

Now just go forward and backward from 27. Enter 28, 29, 30 and then 26, 25, 24, … 1.

Finally, count (or circle) the Saturdays and Sundays. There are 5 of each for a total of 10, so the probability is 

Solution 2. Since the 27th was a Thursday, the 28th, 29th, and 30th were Friday, Saturday, and Sunday, respectively. Repeatedly subtracting 7, you see that the Saturdays were on November 29, 22, 15, 8, 1 and the Sundays were on November 30, 23, 16, 9, 2 for a total of 10 weekend days. Then 

EXAMPLE 9

An integer between 100 and 999, inclusive, is chosen at random. What is the probability that all the digits of the number are odd?

Solution. By KEY FACT O1, since both endpoints are included, there are 999 – 100 + 1 = 900 integers between 100 and 999. In Example 6, you saw that there are 125 three-digit numbers all of whose digits are odd. Therefore, the probability is

Occasionally, on an SAT there will be a question that relates probability and geometry. The next KEY FACT will help you deal with that type of question.

Key Fact O5

If a point is chosen at random inside a geometrical figure, the probability that the chosen point lies in a particular region is:

EXAMPLE 10

In the figure above, a white square whose sides are 4 has been pasted on a black square whose sides are 5. If a point is chosen at random from the large square, what is the probability that the point is in the black area?

Solution. The area of the large square is 5² = 25, and the area of the white square is 4² = 16. Therefore, the area of the black region is 25 – 16 = 9, and the probability that the chosen point is in the black area is 

Exercises on Counting and Probability

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

1.   Let A be the set of primes less than 6, and B be the set of positive odd numbers less than 6. How many different sums of the form a + b are possible if a is in A and b is in B?

(A)   6

(B)   7

(C)   8

(D)   9

(E) 10

2.   Dwight Eisenhower was born on October 14, 1890, and died on March 28, 1969. What was his age, in years, at the time of his death?

(A) 77

(B) 78

(C) 79

(D) 80

(E) 81

3.   There are 27 students in Mr. White’s homeroom. What is the probability that at least 3 of them have their birthdays in the same month?

(A) 0

(B) 

(C) 

(D) 

(E) 1

4.   A jar has 5 marbles, 1 of each of the colors red, white, blue, green, and yellow. If 4 marbles are removed from the jar, what is the probability that the yellow marble was removed?

(A) 

(B) 

(C) 

(D) 

(E) 

5.   A cafeteria has a lunch special, consisting of soup or salad, a sandwich, coffee or tea, and a dessert. If the menu lists 3 soups, 2 salads, 8 sandwiches, and 7 desserts, how many different lunches can you choose? (NOTE: Two lunches are different if they differ in any aspect.)

(A)   22

(B) 280

(C) 336

(D) 560

(E) 672

6.   A printer that can print 1 page in 5 seconds shuts down for 3 minutes to cool off after every hour of operation. How many minutes will the printer take to print 3600 pages?

(A)      300

(B)      312

(C)      315

(D) 18,000

(E) 18,897

7.   In the figure above, how many paths are there from A to X if the only ways to move are up and to the right?

(A) 4

(B) 5

(C) 6

(D) 8

(E) 9

8.   A jar contains 20 marbles: 4 red, 6 white, and 10 blue. If you remove 1 marble at a time, randomly, what is the minimum number that you must remove to be certain that you have at least 2 marbles of each color?

(A)   6

(B) 10

(C) 12

(D) 16

(E) 18

9.   At the audition for the school play, n people tried out. If k people went before Judy, who went before Liz, and m people went after Liz, how many people tried out between Judy and Liz?

(A) n – m – k – 2

(B) n – m – k – 1

(C) n – m – k

(D) n – m – k + 1

(E) n – m – k + 2

Note: Figure not drawn to scale

10. In the figure above, each of the small circles has a radius of 2 and the large circle has a radius of 6. If a point is chosen at random inside the large circle, what is the probability that the point lies in the shaded region?

(A) 

(B) 

(C) 

(D) 

(E) 

Grid-in Questions

11. There are 100 people on a line. Andy is the 37th person, and Ali is the 67th person. If a person on line is chosen at random, what is the probability that the person is standing between Andy and Ali?

12. How many four-digit numbers have only even digits?

13. How many ways are there to rearrange the letters in the word elation, if the first and last letter must each be a vowel?

Questions 14 and 15 refer to the following diagram. A is the set of positive integers less than 20; B is the set of positive integers that contain the digit 7; and C is the set of primes.

14. How many numbers are members of the region labeled x?

15. What is one number less than 50 that is a member of the region labeled y?

Answer Key

1. B   2. B   3. E   4. D

5. D   6. B   7. C   8. E

9. A 10. A

Answer Explanations

  1. B.    A = {2, 3, 5} and B = {1, 3, 5}. Any of the 3 numbers in A could be added to any of the 3 numbers in B, so 9 sums could be formed. However, there could be some duplication. List the sums systematically; first add 1 to each number in A, then 3, and then 5: 3, 4, 6;  There are 7 different sums.

  2. B.     President Eisenhower’s last birthday was in October 1968. His age at death was 1968 – 1890 = 78 years.

  3. E.    If there were no month in which at least 3 students had a birthday, then each month would have the birthdays of at most 2 students. But that’s not possible; even if there were 2 birthdays in January, 2 in February, ...., and 2 in December, only 24 students would be accounted for. It is guaranteed that, with more than 24 students, at least 1 month will have 3 or more birthdays. The probability is 1.

  4. D.    It is equally likely that any 1 of the 5 marbles will be the one that is not removed. Therefore, the probability that the yellow marble is left is  and the probability that it is removed is 

  5. D.     You can choose your first course (soup or salad) in 5 ways, your beverage in 2 ways, your sandwich in 8 ways, and your dessert in 7 ways. The counting principle says to multiply: 5 × 2 × 8 × 7 = 560. (Note that, if you got soup and a salad, then, instead of 5 choices for the first course, there would have been 2 × 3 = 6 choices for the first two courses.)

  6. B.     Use the given information to find the rate of pages per hour.

so 3600 pages will take 3600 ÷ 720 = 5 hours, or 300 minutes, of printing time. There will also be 12 minutes (4 × 3 minutes) when the printer is shut down to cool off, for a total of 312 minutes. Note that there are 5 printing periods and 4 cooling-off periods.

  7. C.    Either label all the vertices and systematically list the possibilities, or systematically trace the diagram. If you start by going from A to B, there are 3 paths: you can get up to the top by BC, EF, or HX, and once there must proceed to the right. Similarly, there are 3 paths if you start by going right from A to D. In all, there are 6 paths from A to X.

  8. E.    In a problem like this one, the easiest thing to do is to see what could go wrong in your attempt to get 2 marbles of each color. If you were really unlucky, you might remove 10 blue ones in a row, followed by all 6 white ones. At that point you would have 16 marbles, and you still wouldn’t have even 1 red. The next 2 marbles, however, must both be red. The answer is 18.

  9. A.    It may help to draw a line and label it. Since k people went before Judy, she was number k + 1 to try out; and since m people went after Liz, she was number n – m to try out. Then, the number of people to try out between Judy and Liz was

10. A.    Since the formula for the area of a circle is r ², the area of each small circle is (2²) = 4. Then the total white area is 8. The area of the large circle is (6²) = 36. Therefore, the area of the shaded region is 36 – 8 = 28, and the probability that a point chosen at random lies in that shaded region is

11. (.29)    There are 67 – 37 – 1 = 29 people between Andy and Ali. The probability that the person chosen is standing between them is

12. (500)    The easiest way to answer this question is to use the counting principle. The first digit can be chosen in any of 4 ways (2, 4, 6, 8), whereas the second, third, and fourth digits can be chosen in any of 5 ways (0, 2, 4, 6, 8). Therefore, the total number of four-digit numbers with only even digits is 4 × 5 × 5 × 5 = 500.

13. (1440)     Again, use the counting principle. How many ways are there to fill in seven blanks, _ _ _ _ _ _ _, with letters from the word elation? Think of this as seven jobs to do. The first job is to choose one of the 4 vowels in the word to be the first letter; the second job is to choose one of the remaining 3 vowels to be the last letter. Thus, there are 4 × 3 = 12 ways to choose the first and last letters. Since there are no other restrictions, the five other jobs are to place the remaining 5 letters in the five remaining blanks. There are 5 choices for the first blank, 4 for the next, then 3, then 2, and finally 1. There are 12 × 5 × 4 × 3 × 2 × 1 = 1440 arrangements.

14. (6)    In the diagram, the region labeled x contains all of the primes less than 20 that do not contain the digit 7. They are 2, 3, 5, 11, 13, 19—6 numbers in all.

15. (37 or 47)    Region y consists of primes that contain the digit 7 and are greater than 20.

9-P Logical Reasoning

All of the questions on the SAT (even the critical reading ones) require some logical reasoning. In fact, the official name of the test is the “SAT Reasoning Test.” However, there are often a few questions on the mathematics sections of the SAT that do not fit into any of the standard mathematics topics. They require “logical reasoning” as opposed to knowledge of a particular fact from arithmetic, algebra, or geometry. Some of the problems don’t even involve numbers or geometric figures. This section and the exercises that follow it present a variety of examples to illustrate the kinds of “logic” questions that you may encounter.

Alphanumeric Problems

An alphanumeric problem is an arithmetic problem in which some or all of the digits have been replaced by letters, and it is your job to determine what numbers the letters represent. The easiest way to explain this is to work out a few examples.

EXAMPLE 1

In the correctly worked out addition problem at the right, each letter represents a different digit. What is the value of A?

Solution. Since the two-digit number AB is less than 100, AB + AB < 200, implying that BCC is a number between 100 and 199. No matter what, B must be 1. Replace each B in the problem with 1.

The addition now looks like this:
Since 1 + 1 = 2, rewrite the problem again, replacing each C with 2:
Finally, since A + A = 12, then A = 6.

Key Fact P1

If the sum of two two-digit numbers is a three-digit number, the first digit of the sum is 1. Similarly, if the sum of two three-digit numbers is a four-digit number, the first digit of the sum is 1.

EXAMPLE 2

In the correctly worked our multiplication problem at the right, each letter represents a different digit. What is the value of A + B + C + D?

Solution. The first step in the multiplication is to multiply A × A. Since 5 is the only digit whose square ends in 5, A must be 5, so replace each A with 5.

The problem now looks like this:
Since 5 × 500 = 2500 and 5 × 600 = 3000, the product CBC5 is someone somewhere between. Therefore, C = 2 and B ≥ 5. Rewrite the problem again, replacing C with 2;
Since A is 5, B isnt't 5, so B is at least 6. Notice that the second digit of 5B5 and the second digit of 2BD5 are the same. But 5 × 565 = 2825; 5 × 575 = 2875; and 5 × 585 = 2925, none of which works.
Try 5 × 595 = 2975, which does
Then B = 9 and D = 7:

A + B + C + D = 5 + 9 + 2 + 7 = 23.

Example 2 is harder than most alphanumerics on an SAT because you have to find the values of all four letters, but the reasoning for each step is exactly what you must be able to do. If the solution wasn’t completely clear, go back and reread it.

Sequences

A sequence is just a list of numbers separated by commas. It can be finite, such as 1, 3, 5, 7, 9; or it can be infinite, such as 5, 10, 15, 20, 25, … . Each number in the list is called a term of the sequence. The terms of a sequence don’t have to follow any pattern or rule, but on the SAT they always do. The most common type of sequence question presents you with a rule for finding the terms of a sequence, and then asks you for a particular term.

TACTIC P1

Never answer a question involving a sequence without writing out at least the first five terms.

EXAMPLE 3

A sequence is formed as follows: the first term is 3, and every other term is 4 more than the term that precedes it. What is the 100th term?

Solution. The sequence begins 3, 7, 11, 15, 19, 23 (7 is 4 more than 3, 11 is 4 more than 7, etc.). Clearly, you could continue writing out the terms, and if the question asked for the 10th term, that would be the easiest thing to do. You are not, however, going to write out 100 terms. What you need now is a little imagination or inspiration. How else can you describe the terms of this sequence? The terms are just 1 less than the corresponding multiples of 4 (4, 8, 12, 16, 20, 24 ...): 7, which is the 2nd term, is 1 less than 2 × 4; 19, which is the 5th term, is 1 less than 5 × 4. Now you have the solution. The 100th term is 1 less than 100 × 4: 400 – 1 = 399.

In Examples 4–6, the sequences S_n are formed as follows:

For any positive integer n: the first term of the sequence S_n is n, and every term after the first is 1 more than twice the preceding term.

EXAMPLE 4

What is the value of the smallest term of S₅ that is greater than 100?

Solution. Sequence S₅ proceeds as follows: 5, 11, 23, 47, 95, 191, ..., so the smallest term greater than 100 is 191.

EXAMPLE 5

What is the units digit of the 500th term of S₉?

Solution. Of course, you’re not going to write out 500 terms of any sequence, but you always write out the first five: 9, 19, 39, 79, 159, … .

There’s no question about it: the units digit of every term is 9.

EXAMPLE 6

If one of the first 10 terms of S₁₀₀₀ is chosen at random, what is the probability that it is odd?

Solution. For any integer m whatsoever, 2m is even and 2m + 1 is odd. The first term of S₁₀₀₀ is 1000, but every other term is odd. The probability is 

Two types of sequences that occasionally appear on the SAT are arithmetic sequences and geometric sequences.

An arithmetic sequence is a sequence such as the one in Example 3, in which the difference between any two consecutive terms is the same. In Example 3 that difference was 4. An easy way to find the nth term of such a sequence is to start with the first term and add the common difference n – 1 times. In Example 3, the sixth term is 23, which can be obtained by taking the first term, 3, and adding the common difference, 4, five times: 3 + 5(4) = 23. In the same way, the 100th term is 3 + 99(4) = 3 + 396 = 399.

Key Fact P2

If a₁, a₂, a₃, … is an arithmetic sequence whose common difference is d, then a_n = a₁ + (n – 1) d.

A geometric sequence is a sequence in which the ratio between any two consecutive terms is the same. For example, the sequence, 2, 10, 50, 250, 1250, … is a geometric sequence: the ratios  are all equal to 5.

An easy way to find the nth term of a geometric sequence is to start with the first term and multiply it by the common ratio n – 1 times. For example, in the sequence 2, 10, 50, 250, 1250, … the fourth term is 250, which can be obtained by taking the first term, 2, and multiplying it by the common ratio, 5, three times: 2 × 5 × 5 × 5 = 2 × 5³ = 2 × 125 = 250. In the same way, the 100th term is 2 × 5⁹⁹.

Key Fact P3

If a₁, a₂, a₃, … is a geometric sequence whose common ratio is r, then a_n = a₁ (r)^{n – 1}.

Consider the following three sequences:

(i) 1, 7, 13, 19, 25, 31, …

(iii) 1, 2, 3, 5, 8, 13, …

Sequence (i) is an arithmetic sequence in which the common difference is 6. A reasonable SAT question would be: What is the 75th term of this sequence? By KEY FACT P2, the answer is 1 + 74(6) = 1 + 444 = 445. This could be a multiple-choice or a grid-in question.

Sequence (ii) is a geometric sequence in which the common ratio is  A reasonable SAT question would be: What is the 75th term of this sequence? By KEY FACT P3, the answer is  This could only be a multiple-choice question because there is no way to grid in such an answer. It is likely that one of the answer choices would, in fact, be But since

the correct answer choice could also be 

Sequence (iii) is neither an arithmetic sequence nor a geometric sequence: there is no common difference (13 – 8 ≠ 8 – 5), and there is no common ratio

Therefore, you have no formula for evaluating the nth term of this sequence, and it would not be reasonable to ask for the 75th term. If you were told that the rule for the sequence is that each term is the sum of the two preceding terms (3 = 1 + 2, 5 = 2 + 3, 8 = 3 + 5, …), then it would be reasonable to ask: What is the smallest term in this sequence that is greater than 100? The answer is 144, which you could get just by calculating five more terms. 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.

In some sequences the terms repeat in a cyclical pattern.

TACTIC P2

When k numbers form a repeating sequence, to find the nth number, divide n by k and take the remainder r. The rth term and the nth term are the same.

Examples 7 and 8 refer to the infinite sequence 1, 4, 2, 8, 5, 7, 1, 4, 2, 8, 5, 7,..., in which the six digits 1, 4, 2, 8, 5, and 7 keep repeating in that order.

EXAMPLE 7

What is the 500th term of the sequence?

Solution. When 500 is divided by 6, the quotient is 83 (6 × 83 = 498) and the remainder is 2.

Therefore, the first 498 terms are just the numbers 1, 4, 2, 8, 5, 7 repeated 83 times. The 498th term is the 83rd 7 in the sequence. Then the pattern repeats again: the 499th term is 1, and the 500th term is 4.

In this example, notice that the 500th term is the same as the 2nd term. This occurs because 2 is the remainder when 500 is divided by 6.

EXAMPLE 8

What is the sum of the 800th through the 805th terms of the sequence?

Solution. Don’t waste time determining what the 800th term is. Any six consecutive terms of the sequence consist, in some order, of exactly the same six numbers: 1, 4, 2, 8, 5, and 7. Their sum is 27.

Patterns

Some SAT questions are based on repeating patterns. These are very similar to repeating sequences, except that the terms don’t have to be numbers.

EXAMPLE 9

In order to divide the campers at a camp into six teams (the reds, whites, blues, greens, yellows, and browns), the director had all the campers form a line. Then, starting with the first person, each camper on line called out a color, repeating this pattern: red, white, blue, green, yellow, brown, red, white, blue, green, yellow, brown, .... What color was called out by the 500th camper?

(A) Red

(B) White

(C) Green

(D) Yellow

(E) Brown

Solution. This is exactly the same as Example 9. When 500 is divided by 6, the quotient is 83 and the remainder is 2. Then, by TACTIC P2, the 500th camper called out the same color as the 2nd camper: white (B).

EXAMPLE 10

Last year Elaine’s birthday was on Friday. If Susan’s birthday was 150 days after Elaine’s, how many Sundays were there between Elaine’s birthday and Susan’s birthday?

Solution. The 7 days of the week repeat in cyclical pattern. Using TACTIC P2, divide 150 by 7, getting a quotient of 21 and a remainder of 3. Thus, the 150th day after Elaine’s birthday was Monday, the same as the 3rd day after her birthday. During the 21 full weeks between Elaine’s and Susan’s birthdays, there were 21 Sundays, and there was 1 more during the last 3 days, for a total of 22.

Exercises on Logical Reasoning

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

1. In the correctly worked out addition problem at the right, each letter represents a different digit. What is the value of A?

(A) 5

(B) 6

(C) 7

(D) 8

(E) 9

2. In the United States, Thanksgiving is celebrated on the fourth Thursday in November. Which of the following statements is (are) true?

  I. Thanksgiving is always the last Thursday in November.

 II. Thanksgiving is never celebrated on November 22.

III. Thanksgiving cannot be celebrated on the same date 2 years in a row.

(A) None

(B) I only

(C) II only

(D) III only

(E) I and III only

3. A gum-ball dispenser is filled with exactly 1000 pieces of gum. The gum balls always come out in the following order: 1 red, 2 blue, 3 green, 4 yellow, and 5 white. After the fifth white, the pattern repeats, starting with 1 red, and so on. What is the color of the last gum ball to come out of the machine?

(A) Red

(B) Blue

(C) Green

(D) Yellow

(E) White

4. The Declaration of Independence was signed in July 1776. What month and year was it 500 months later?

(A) March 1817

(B) August 1817

(C) November 1817

(D) March 1818

(E) May 1818

5. In the correctly worked out multiplication problem at the right, each letter represents a different digit. What is the value of A + B+C?

(A) 12

(B) 15

(C) 18

(D) 21

(E) 27

6. If a population that is initially 100 triples every year, which of the following is an expression for the size of the population after t months?

Grid-in Questions

7. In the correctly worked out addition problem below, each letter represents a different digit. What is the number CBA?

8. Three children guessed the number of jelly beans in a jar. The guesses were 98, 137, and 164. None of the guesses was correct. One guess was off by 12, another by 27, and the third by 39. How many jelly beans were in the jar?

9. The pointer on the dial below moves 3 numbers clockwise every minute. If it starts at 1, what number will it be pointing to in exactly 1 hour?

10. A sequence is formed by choosing a number, x, to be the first term. Every term after the first is y more than the preceding term. If the 8th term is 19 and the 12th term is 29, what is xy?

Answer Key

1. C   2. D

3. D   4. D

5. B   6. C

Answer Explanations

1. C. By KEY FACT P1, B = 1, so the sum looks like this:
If A ≤ 6, then the A + 3 in each column will be a one-digit number, so A is at least 7. In fact, 7 works.

2. D. If November 1 is a Thursday, then so are November 8, 15, 22, and 29. Therefore, Thanksgiving could fall on November 22 (II is false); and if it does, it is not the last Thursday in November (I is false). Assume that one year Thanksgiving falls on Thursday, November X. Then exactly 52 weeks (or 7 × 52 = 364 days) later it will again be Thursday, but it won’t be November X, because November X comes 365 (or 366) days after the preceding November X (III is true).

3. D. Since the pattern repeats itself after every 15 gum balls, divide 1000 by 15. The quotient is 66, and the remainder is 10. Therefore, the 1000th gum ball is the same color as the 10th, which is yellow.

4. D.  The 12 months of the year form a repeating sequence.   500 ÷ 12 = 41.666…. and 41 × 12 = 492. Therefore, exactly 41 years (or 492 months) after July 1776 it will be July in the year 1776 + 41 = 1817. Since 500 – 492 = 8, 500 months after July 1776 is 8 months after July 1817, which is March 1818.

5. B. Since AB < 100, 3 times AB is less AB than 3 × 100 = 300, so C is 1 or 2. Since 3 times B ends in B, B is CBB either 0 or 5. It can’t be 0 because neither 100 nor 200 is a multiple of 3: so B = 5.

The simplest thing to do now is test A5 whether 155 or 255 is a multiple of 3: 155 isn’t, but 255 = 3 × 85. Then C = 2 and A = 8. Finally, A + B + C = 8 + 5 + 2 = 15.

6. C. Since t months is  years, the population triples  times. After t months, the population will be 

7. (135) A can’t be 0, and the only other digit A that, multiplied by 3, ends in A is 5 (3 × 5 = 15). A = 5, and CBA = 35 + 45 + 55 = 135.

8. (125)There are lots of ways to reason this out. Here is one. The number must be over 100; otherwise the guess of 164 would be off by more than 64, and none of the guesses was that far wrong, Thus, the guess of 98 was too low. If it was 12 too low, there would be 110 jelly beans, but then 164 would be off by 54, which isn’t right. If 98 was 27 too low, the number would be 125, which is 12 less than 137 and 39 less than 164. That’s it.

9. (6)To see the pattern develop, write out the locations of the pointer for the first few minutes. Advancing 3 numbers per minute, it goes from 1→ 4→ 7→ 3→ 6→ 2→ 5→ 1; and when it is back to 1, the whole cycle repeats. To know where the pointer will be in 60 minutes, divide 60 by 7. Since the quotient is 8 and the remainder is 4, after 60 minutes the pointer will be pointing to the same number it pointed to after 4 minutes. Be careful. That number is not 3; it’s 6. After 1 minute the pointer is at 4, after 2 minutes it’s at 7, and so on.
Alternative solution. Since the pointer advances 3 numbers per minute, it advances 3 × 60 = 180 minutes per hour. Dividing 180 by 7 gives a quotient of 25 and a remainder of 5, so the pointer makes 25 complete cycles and then advances 5 more numbers, from 1 to 6.

10.  Each term is y more than the preceding term; therefore, the 9th term is 19 + y, the 10th term is 19 + y + y = 19 + 2y, the 11th term is 19 + 2y + y = 19 + 3y, and the 12th term is 19 + 3y + y = 19 + 4y. But the 12th term is 29, so

29 = 19 + 4y ⇒ 10 = 4y ⇒ y = 2.5.

You could now count backward from the 8th term to the 1st term, subtracting 2.5 each time. Instead, note that, to get from the 1st to the 8th term, it was necessary to add 2.5 seven times. Therefore:
x + (7 × 2.5) = 19 ⇒ x + 17.5 = 19 ⇒ x = 1.5.
Finally, 

9-Q Interpretation of Data

Typically, the SAT has a few questions that require you to interpret and/or manipulate the data that appear in some type of table or graph. The graphs will be no more complicated, and probably will be simpler, than the ones that you usually see in newspapers and magazines or in your science or social studies textbooks.

Sometimes you are asked two questions based on the same set of data. In this case, the first question is usually quite easy, requiring only that you read the information in the table or graph. The second question is usually a little more challenging and may ask you to interpret the data, or manipulate them, or make a prediction based on them.

Helpful Hint

Before even reading the questions based on a graph or table, take 10 or 15 seconds to look it over. Make sure you understand the information that is being displayed and the units of the quantities involved.

The data can be presented in the columns of a table or displayed graphically. The graphs that appear most often are bar graphs, line graphs, circle graphs, and scatter-plot diagrams. This section illustrates each of these and gives examples of the types of questions that may be asked.

Although the second hint is good advice on all SAT questions, it is particularly important on table and graph problems because there is so much information that can be used, and so many different questions can be asked.

Let’s start by looking at a line graph. A line graph indicates how one or more quantities change over time. The horizontal axis is usually marked off in units of time; the units on the vertical axis can represent almost any type of numerical data: dollars, weights, exam grades, number of people, and so on.

Here is a typical line graph:

Helpful Hint

After looking over the entire graph, read the first question. Be clear about what is being asked, and circle it in your test booklet. Answer the questions based only on the information provided in the graph.

Before reading even one of the questions based on the above graph, you should have acquired at least the following information:

(i) The graph gives the values of two different stocks.

(ii) The graph covers the period from January 1, 2005, to January 1, 2010.

(iii) During that time, both stocks rose in value.

There are literally dozens of questions that could be asked about the data in this graph. The next seven examples are typical of the types of questions that appear on the SAT.

EXAMPLE 1

What is the difference, in dollars, between the highest and lowest values of a share of stock A?

Solution. The lowest value of stock A was $25 (in 2005); the highest value was $40 (in 2010). The difference is $15.

EXAMPLE 2

On January 1 of what year was the difference in the values of a share of stock A and a share of stock B the greatest?

Solution. Just look at the graph. The difference was clearly the greatest in 2007. (Note that you don’t have to calculate what the difference was.)

EXAMPLE 3

On January 1 of what year was the ratio of the value of a share of stock A to the value of a share of stock B the greatest?

Solution. From 2008 to 2010 the values of the two stocks were fairly close, so those years are not candidates. In 2007 the ratio was 40:10 or 4:1 or 4. In 2006 the ratio was 35:20 or 7:4 or 1.75. In 2005 the ratio was 30:10 or 3:1 or 3. The ratio was greatest in 2005.

EXAMPLE 4

In what year was the percent increase in the value of a share of stock B the greatest?

Solution. Just look at the graph. Since the slope of the graph is steepest in 2007 (between January 1, 2007 and January 1, 2008), the rate of growth was greatest then.

EXAMPLE 5

During how many years did the value of stock B grow at a faster rate than that of stock A?

Solution. Again, look at the slopes.

• In 2005, B rose more sharply than A. 

• In 2006, B fell while A rose.

• In 2007, B rose while A fell. 

• In 2008, A rose more sharply than B.

• In 2009, A rose; B stayed the same.

B grew at a faster rate during 2 years.

EXAMPLE 6

What was the average yearly increase in the value of a share of stock A from 2005 to 2010?

Solution. Over the 5-year period from January 1, 2005, to January 1, 2010, the value of a share of stock A rose from $30 to $45, an increase of $15. The average yearly increase was $15 ÷ 5 years or $3 per year.

EXAMPLE 7

If from 2005 to 2015 the value of each stock increases at the same rate as it did from 2005 to 2010, what will then be the ratio of the value of a share of stock B to the value of a share of stock A?

Solution. From 2005 to 2010, the value of stock A increased by 50% (from $30 to $45) and the value of stock B quadrupled (from $10 to $40). At the same rates, stock A will grow from $45 to $67.50 in the years 2010–2015, while stock B will grow from $40 to $160. The ratio of the value of a share of stock B to the value of a share of stock A will be 160 to 67.5, or approximately 2.37.

To answer these seven questions, most (but not all) of the data contained in the graph was used. On the SAT, if you had two questions based on that line graph, you can see that there would be many items of information you would not use.

Helpful Hint

On data interpretation questions ignore the extraneous information you are given. Zero in on exactly what you need.

The same information that was given in the preceding line graph could have been presented in a table or in a bar graph.

PRICE PER SHARE OF STOCKS A AND B ON
JANUARY 1 OF 6 YEARS

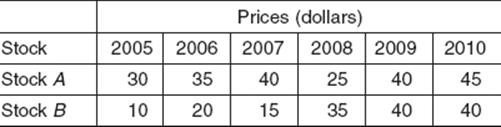
PRICE PER SHARE OF STOCKS A AND B ON 
JANUARY 1 OF 6 YEARS

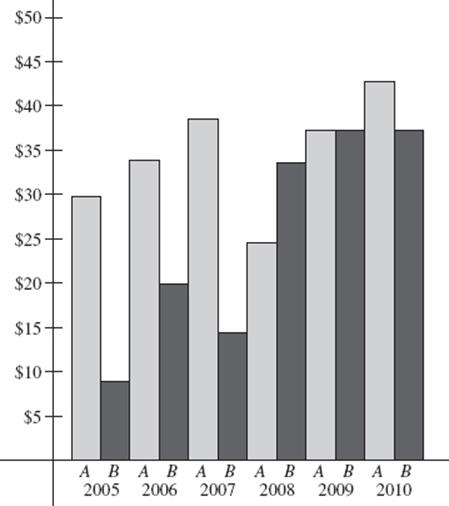
In a bar graph, the taller the bar, the greater is the value of the quantity. Bar graphs can also be drawn horizontally; in that case the longer the bar, the greater is the quantity. You will see examples of each type in the exercises at the end of this section, in the model tests, and, of course, on the SAT.

The following bar graph shows the numbers of students taking courses in the various foreign languages offered at a state college.

NUMBERS OF STUDENTS ENROLLED IN
LANGUAGE COURSES AT STATE COLLEGE IN 2010

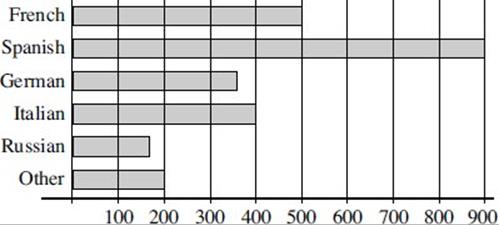
In a slight variation of the horizontal bar graph, the bars are replaced by a string of icons, or symbols. For example, the graph below, in which each picture of a person represents 100 students, conveys the same information as does the preceding bar graph.

NUMBERS OF STUDENTS ENROLLED IN 
LANGUAGE COURSES AT STATE COLLEGE IN 2010

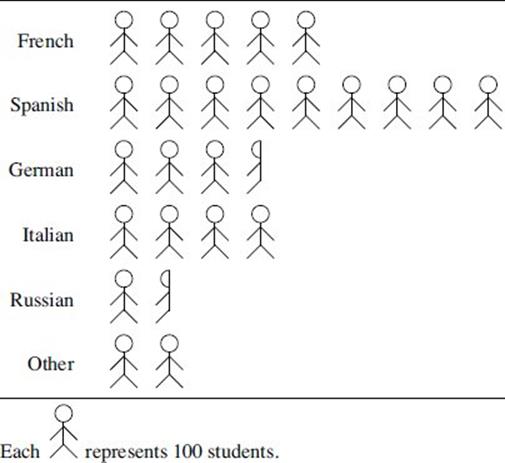
From either of the two preceding graphs, many questions could be asked. Examples 8–10 illustrate a few types.

EXAMPLE 8

What is the total number of students enrolled in language classes in 2010?

Solution. Just read the graph and add: 2500.

EXAMPLE 9

If the “Other” category includes five languages, what is the average (arithmetic mean) number of students studying each language offered at the college?

Solution. There are 2500 students divided among 10 languages (the 5 listed plus the 5 in the “Other” category): 2500 ÷ 10 = 250.

EXAMPLE 10

If the number of students studying Italian in 2011 was the same as the number taking Spanish in 2010, by what percent did the number of students taking Italian increase?

Solution. The number of students taking Italian increased by 500 from 400 to 900. This represents a  increase.

A circle graph is another way to present data pictorially. In a circle graph, which is sometimes called a pie chart, the circle is divided into sectors, with the size of each sector exactly proportional to the quantity it represents.

For example, the information included in the preceding bar graph is presented in the following circle graph.

NUMBERS OF STUDENTS ENROLLED IN 
LANGUAGE COURSES AT STATE COLLEGE IN 2010

Usually on the SAT, in each sector of the circle is noted the number of degrees of its central angle or the percent of the total data it contains. For example, in the circle graph above, since in 2010, 500 of the 2500 language students at State College were studying French, the sector representing French is exactly  of the circle. On the SAT this sector would also be marked either  The SAT graph would look like one of the graphs below.

DISTRIBUTION OF THE 2500 STUDENTS 
ENROLLED IN LANGUAGE COURSES

DISTRIBUTION OF THE 2500 STUDENTS 
ENROLLED IN LANGUAGE COURSES

Very often on the SAT, some data are omitted from a circle graph, and it is your job to determine the missing item. Examples 11 and 12 are based on the following circle graph, which shows the distribution of marbles by color in a large jar.

EXAMPLE 11

If the jar contains 1200 marbles and there are twice as many orange marbles as there are green, how many green marbles are there?

Solution. Since the red, blue, and yellow marbles constitute 75% of the total (30% + 25% + 20%), the orange and green ones combined account for 25% of the total: 25% of 1200 = 300. Then, since the ratio of orange marbles to green ones is 2:1, there are 200 orange marbles and 100 green ones.

EXAMPLE 12

Assume that the jar contains 1200 marbles, and that all of the red ones are removed and replaced by an equal number of marbles, all of which are blue or yellow. If the ratio of blue to yellow marbles remains the same, how many additional yellow marbles are there?

Solution. Since 30% of 1200 is 360, the 360 red marbles were replaced by 360 blue and yellow ones. To maintain the current blue to yellow ratio of 25 to 20, or 5 to 4,  of the new marbles would be blue and would be yellow: of 360 = 160.

Exercises on Interpretation of Data

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

Questions 1–3 refer to the following graph.

SPEEDS AT WHICH MARC DROVE 
ON SUNDAY MORNING

  1. For what percent of the time was Marc driving at 40 miles per hour or faster?

(A) 20

(B) 25

(D) 40

(E) 50

  2. How far, in miles, did Marc drive between 8:30 and 9:00?

(A) 0

(B) 20

(C) 30

(D) 40

(E) It cannot be determined from the information given.

  3. What was Marc’s average speed, in miles per hour, between 8:30 and 9:30?

(A) 40

(C) 42.5

(D) 45

(E) It cannot be determined from the information given.

Questions 4–6 refer to the following graph.

CRITICAL READING SAT SCORES OF ALL THE 
JUNIORS AT CENTRAL HIGH SCHOOL

  4. How many juniors at Central High School took the SAT?

(A) 1000

(B) 1100

(C) 1200

(D) 1250

(E) 1300

  5. What percent of the juniors had Critical Reading SAT scores of less than 600?

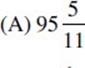
(D) 80

(E) It cannot be determined from the information given.

  6. How many juniors had Critical Reading SAT scores between 450 and 550?

(A) 360

(B) 375

(C) 525

(D) 750

(E) It cannot be determined from the information given.

Questions 7 and 8 refer to the following graph.

2010 SMITH FAMILY HOUSEHOLD BUDGET

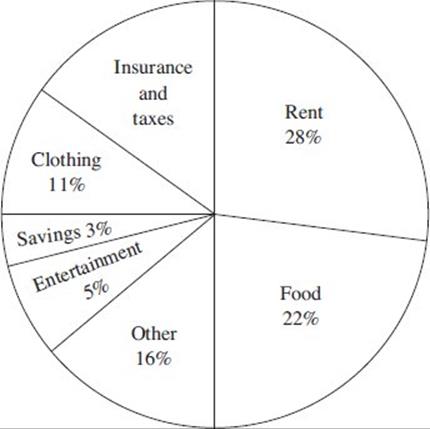
  7. If the Smiths’ income in 2010 was $40,000, how much more did they spend on insurance and taxes than they did on clothing?

(A) $1600

(B) $2000

(C) $3200

(D) $4400

(E) $6000

  8. What is the degree measure of the central angle of the sector representing insurance and taxes?

(A) 45

(B) 54

(C) 60

(D) 72

(E) 90

Grid-in Questions

Questions 9 and 10 refer to the following graph.

DISTRIBUTION OF GRADES OF 500 STUDENTS ON THE FINAL EXAM IN MATH

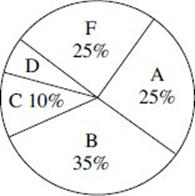
  9. How many students earned a grade of D?

10. What percent of the students who failed the exam would have had to pass it, in order for the percent of students passing the exam to be at least 85%?

Answer Key

1. E   2. B   3. C

4. B   5. C   6. E

7. A   8. B

 

Answer Explanations

1. E. Of the  hours (from 8:00 until 10:30) that Marc was driving, he was going 40 miles per hour or faster for  hours (from 8:30 until 9:45). Therefore, he was driving at 40 miles per hour or faster 50% of the time.

2. B. During the half hour between 8:30 and 9:00, Marc was driving at a constant rate of 40 miles per hour, so he drove  miles.

3. C. From the graph it is clear that, from 9:00 to 9:30, Marc’s speed increased steadily from 40 to 50 miles per hour and that his average speed was 45 miles per hour. From 8:30 to 9:00 his average speed was clearly 40 miles per hour. Then, for the entire hour, he averaged  miles per hour.

4. B.  Just read the graph carefully, and add the numbers of juniors who had scores in each range:

50 + 100 + 400 + 350 + 150 + 50 = 1100.

5. C.  Of the 1100 students, 900 had scores less than

6. E. There is no way of knowing. It is possible, though very unlikely, that all of the scores between 400 and 590 were between 400 and 420 or 570 and 590, and that no one scored between 450 and 550. Undoubtedly, some did, but you can’t tell how many.

7. A.  The total percent for the six categories for which percents are given is 28 + 22 + 16 + 5 + 3 + 11 = 85, so the percent of their income that the Smiths spend on insurance and taxes is 15%. Since they spend 11% on clothing, the difference between the two categories is 4%. Finally, 4% of $40,000 is $1600.

8. B.  Since insurance and taxes take up 15% of the Smiths’ income (see solution 7), the sector representing insurance and taxes must be 15% of the circle. The degree measure of the central angle for this sector is 15% of 360 = 54.

9. (25) Since 25% + 35% + 10% + 25% = 95% of the students earned grades of A, B, C, or F, 5% earned grades of D: 5% of 500 = 25.

10. (40)  For the passing rate to have been at least 85%, no more than 75 students (15% of 500) could have failed. Of the 125 students (25% of 500) who actually failed, 50 of them would have had to pass: 50 of 125 is 40%.

9-R Functions and Their Graphs

You have undoubtedly studied functions many times in your math classes. However, most of what you learned about functions is not tested on the SAT. This section reviews the basic facts about functions and their graphs that you do need for the SAT.

As used on the SAT, a function is a rule that assigns to each number in one set a number in another set. The function is usually designated by the letter f, although other letters such as g and h are sometimes used. The numbers in the first set are labeled x, and the number in the second set to which x is assigned by the function is designated by the letter y or by f(x).

For example, we can write y = f(x) = 2x + 3. This function assigns, to each real number x, the number 2x + 3.

The number assigned to 5 is 2(5) + 3 = 10 + 3 = 13, and the number assigned to –5 is 2(–5) + 3 = –10 + 3 = –7.

To express these facts, we write

f(5) = 13 and f(–5) = –7.

The proper way to think of the function f(x) = 2x + 3 is that f takes anything and assigns to it 2 times that thing plus 3:

f(anything) = 2(that thing) + 3.

• f(100) = 2(100) + 3 = 203

• f(0) = 2(0) + 3 = 0 + 3 = 3

• f(a) = 2a + 3

• f(a + b) = 2(a + b) + 3

• f(x²) = 2x ² + 3

• f(2x ² + 3) = 2(2x ² + 3) + 3 = 4x ² + 9

• f(f(x)) = 2(f(x)) + 3 = 2(2x + 3) + 3 = 4x + 6 + 3 = 4x + 9

EXAMPLE 1

If f(x) = x² + 2x, what is f(3) + f(–3)?

Solution.     f(3) = 3² + 2(3) = 9 + 6 = 15,

                   f(–3) = (–3)² + 2(–3) = 9 – 6 = 3.

Then            f(3) + f(–3) = 15 + 3 = 18.

EXAMPLE 2

If f(x) = x² + 2x, what is f(x + 2)?

(A) x² + 2x + 4

(B) x² + 2x + 8

(C) x² + 6x + 4

(D) x² + 6x + 8

(E) x³ + 4x² + 4x

Solution. f(x + 2) = (x + 2)² + 2(x + 2) = (x² + 4x + 4) + (2x + 4) = x² + 6x + 8 (D).

Sometimes on the SAT, you are asked a question that tests both your understanding of what a function is and your ability to do some basic algebra. The following example does just that.

EXAMPLE 3

If f(x) = 3x + 3, for what value of a is it true that 3f(a) = f(2a)?

(A) –3

(B) –2

(C)   0

(D)   2

(E)   3

Solution.     3f(a) = 3(3a + 3) = 9a + 9,

                   f(2a) = 3(2a) + 3 = 6a + 3.

The graph of a function, f, is a certain set of points in the coordinate plane. Point (a, b) is on the graph of f if and only if b = f(a). For example, the graph of f(x) = 2x + 3 consists of all points (x, y) such that y = 2x + 3. Since f(5) = 13 and f(–5) = –7, then (5, 13) and (–5, –7) are both points on the graph of f(x) = 2x + 3. In Section 9-N, you saw that the graph of y= 2x + 3 is a line whose slope is 2 and whose y-intercept is 3.

On the SAT you may have to know whether a certain point is on the graph of a given function, but you won’t have to actually graph the function.

EXAMPLE 4

Which of the following is NOT a point on the graph of

(A) (1, 5)

(B) (–1, 5)

(C) (2, 5)

(D) (–2, –5)

(E) (4, 16.25)

Solution.

Test each answer choice until you find one that does NOT work.

The answer is choice D.

EXAMPLE 5

Which of the following could be the equation of the graph shown in the figure above?

(A) y = –2x + 4

(B) y = 2x + 4

(C) y = x²

(D) y = 2x² – 4

(E) y = x² – 4x + 4

Solution. Since the graph passes through (2, 0), x = 2 and y = 0 must satisfy the equation. Test each of the five choices in order.

• (A) Does 0 = –2(2) + 4?                    Yes

• (B) Does 0 = 2(2) + 4?                       No

• (C) Does 0 = 2²?                                No

• (D) Does 0 = 2(2²) – 4?                      No

• (E) Does 0 = 2² – 4(2) + 4?                 Yes

The answer is A or E. To break the tie, try another point on the graph, say (0, 4) and test choices A and E.

• (A) Does 4 = –2(0) + 4? Yes

• (E) Does 4 = (0)2 – 4(0) + 4? Yes

Unfortunately, that didn’t help. Try one more, point (1, 1).

• (A) Does 1 = –2(1) + 4? No

• (E) Does 1 = 1² – 4(1) + 4? Yes

The answer is y = x² – 4x + 4 (E).

You can think of a function as a machine. A washing machine performs a function. It cleans clothes: dirty clothes go in and clean clothes come out. In the same way you can think of f(x) = 2x + 3 as a machine. When 5 goes in, 13 comes out; when –5 goes in, –7 comes out.

The domain of a function is the set of all real numbers that can go into the machine without causing a problem. The domain of f(x) = 2x + 3 is the set of all real numbers, because, for any real number whatsoever, you can double it and add 3. No number will cause the machine to jam.

, however, the domain is not the set of all real numbers. Although 5 is in the domain of f, because,  is not in the domain of f. The reason is that , which is not a real number. If you try to evaluate  on your calculator (a machine that evaluates many functions), you will get an error message. Since the domain of a function is the set of all real numbers except those that cause problems, you need to know what can cause a problem. Many things can be troublesome, but for the SAT you need to know about only two of them.

Key Fact R1

A number x is not in the domain of y = f (x) if evaluating f (x) would require you to divide by 0 or to take the square root of a negative number.

EXAMPLE 6

Which of the following numbers is NOT in the domain of ?

(A) –6

(B) –4

(C)   0

(D)   4

(E)   6

Solution. Since you cannot take the square root of a negative number, the domain of  is the set of all real numbers x such that  Only 6, E is not in the domain.

Note that 4 is in the domain of  because . But 4 is not in the domain of  because , which is undefined. Remember, you can never divide by 0.

Again, if a function is thought of as a machine, the range of a function is the set of all real numbers that can come out of the machine. Recall that, if f(x) = 2x + 3, then f(5) = 13 and f(–5) = –7, so 13 and –7 are both in the range of f(x). In general, it is much harder to find the range of a function than to find its domain, but you will usually be able to test whether a particular number is in the range.

EXAMPLE 7

Which of the following is NOT in the range of f(x) = x² – 3?

(A)   6

(B)   1

(C)   0

(D) –1

(E) –6

Solution. Since for any real number x, x² ≥ 0, then x² – 3 ≥ –3. Therefore, –6 (E) is not in the range of f(x).

Note that in the solution to Example 6 you do not have to test each of the choices, but you can. To test whether 6 is in the range of f(x), see whether there is a number x such that f(x) = 6: 

Then f(3) = 6, and 6 is in the range. Similarly, f(2) = 1, f()=0, and f()= –1, so 1, 0, and –1 are also in the range. If you test –6, you see that f(x) = –6 ⇒x² – 3 = –6 ⇒ x² = –3.

But there is no real number whose square is –3. Nothing that can go into the machine will cause –6 to come out.

On the SAT, questions such as Examples 5 and 6 above may be phrased without using the words “domain” and “range.” For example, Example 5 may be expressed as follows:

The function  is defined for each of the following numbers EXCEPT

(A) –6

(B) –4

(C)   0

(D)   4

(E)   6

Similarly, Example 7 may be expressed as follows:

For the function f(x) = x² – 3, which of the following numbers may NOT be the value of f(x)?

(A)   6

(B)   1

(C)   0

(D) –1

(E) –6

On the SAT you take, it is likely that there will be one question that shows you a graph and asks you which of five other graphs is related to the original one in a certain way. To answer such a question, you can either test points or use the five facts listed in the following KEY FACT.

Key Fact R2

If f(x) is a function and r is a positive number:

1. The graph of y = f (x) + r is obtained by shiftingthe graph of y = f (x) UP r units.

2. The graph of y = f (x) – r is obtained by shifting the graph of y = f (x) DOWN r units.

3. The graph of y = f (x + r) is obtained by shifting the graph of y = f (x) r units to the LEFT.

4. The graph of y = f (x – r) is obtained by shifting the graph of y = f (x) r units to the RIGHT.

5. The graph of y = –f (x) is obtained by reflecting the graph of y = f (x) in the x-axis.

Each part of KEY FACT R2 is illustrated below.

Figure (a) is the graph of the absolute-value function: y = f(x) = |x|. Figures (b)–(f) are transformations of the original graph.

EXAMPLE 8

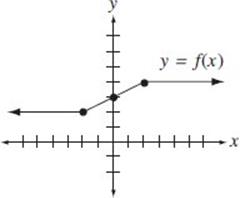
If the figure above is the graph of y = f(x), which of the following is the graph of y = f(x + 2)?

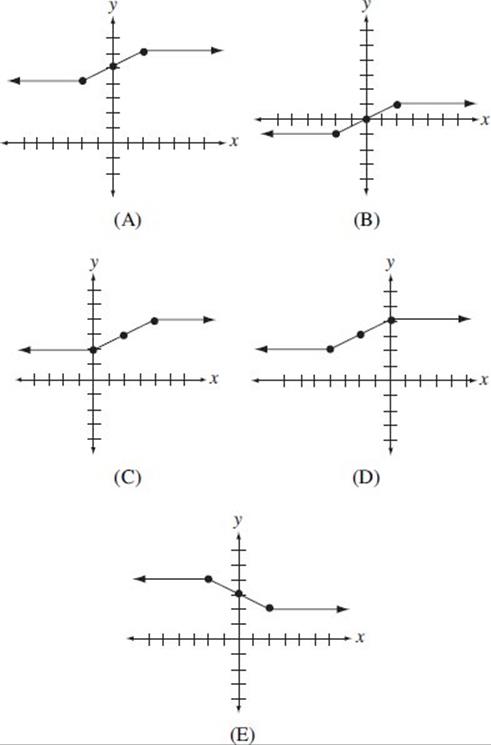
Solution 1. Since (0, 3) is a point on the graph of y = f(x), f(0) = 3. Then 3 = f(0) = f(–2 + 2) and so (–2, 3) is a point on the graph of y = f(x + 2). Only choice D passes through (–2, 3). Note that, if two or three of the graphs passed through (–2, 3), you would test those graphs with a second point, say (2, 4).

Solution 2. By KEY FACT R2, the graph of y = f(x + 2) results from shifting the graph of y = f(x) 2 units to the left. Only choice D is 2 units to the left of the graph in question.

Exercises on Functions and Their Graphs

NOTE: On all the model tests in this book, the difficulty level of the math questions in each section proceeds from easy to medium to hard, just as they do on all real SATs. The questions in this exercise set, however, are not presented in any particular order of difficulty.

Multiple-Choice Questions

Questions 1–4 concern the function y = f (x) = , whose graph is shown below. Choices (A)–(E) are graphs of functions that are somehow related to f(x).

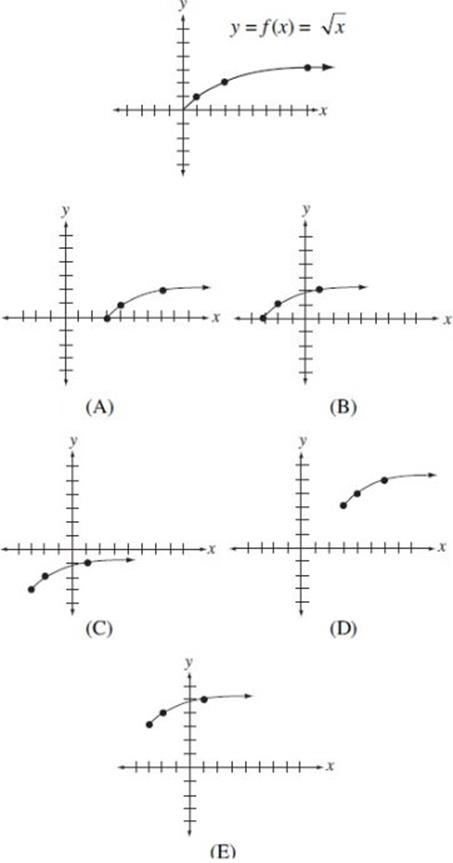
1. Which of the graphs is the graph of y = f (x – 3)?

(A) A

(B) B

(C) C

(D) D

(E) E

2. What is the domain of the function y = f(x – 3)?

(A) All real numbers

(B) All real numbers except 3

(C) All real numbers greater than 3

(D) All real numbers greater than or equal to 3

(E) All real numbers less than 3

3. Which of the graphs is the graph of y = f(x + 3) + 3?

(A) A

(B) B

(C) C

(D) D

(E) E

4. If g(x) = f(f(x)), what is g(4)?

(A) 4

(B) 2

(C) 1

(D) 

(E) 2

5. If f(x) = |x|, for what value of x does f(x – 3) = f(x + 3)?

(A) –3

(B) 0

(C) 3

(D) No value of x

(E) All values of x

Grid-in Questions

6. If f(x) = x² – 2^x, what is the value of f(3)?

7. What is the smallest integer that is NOT in the domain 

Questions 8 and 9 concern the function f(x)= 8 – 2x².

8. How many integers satisfy the condition that f(x) is positive?

9. How many positive integers are in the range of f(x)?

10. If f(x) = x + 5, for what value of x does f(4x) = f(x + 4)?

Answer Key

1. A   2. D   3. E

4. D   5. B

Answer Explanations

1. A. The graph of y = f(x – 3) is the result of shifting the given graph 3 units to the right.

2. D. The domain of  is the set of all real numbers such that x – 3 ≥ 0. So, the domain consists of all real numbers greater than or equal to 3.

3. E. To get the graph of y = f(x + 3), you need to shift the original graph 3 units to the left (this is graph (B)). Then, to get the graph of y = f(x + 3) + 3, shift graph (B) 3 units up, yielding graph (E).

4. D. 

5. B. 
which is impossible, or

Then x= –x, and so x = 0.

6. (1) f(3) = 3²–2³ = 9 – 8 = 1.

7. (4) Since you can’t take the square root of a negative number, the domain of f(x) consists of every real number, x, such that π – x ≥ 0. The numbers that are not in the domain of f(x) satisfy the inequalitysmallest integer greater than π is 4.

8. (3) 
The only integers whose squares are less than 4 are –1, 0, and 1; there are 3 of them. Note that f(2) and f(–2) are both 0, which is not positive.

9. (8) Since x², and hence 2x², must be greater than or equal to 0, the maximum value of f(x) is 8. This means that 8 is the largest number in the range of f(x). In fact, every number less than or equal to 8 is in the range. There are 8 positive integers in the range: 1, 2, 3, 4, 5, 6, 7, 8. For example, f(0) = 8, f(1) = 6, 

10.