CHEMISTRY THE CENTRAL SCIENCE
12 SOLIDS AND MODERN MATERIALS
12.3 METALLIC SOLIDS
Metallic solids, also simply called metals, consist entirely of metal atoms. The bonding in metals is too strong to be due to dispersion forces, and yet there are not enough valence electrons to form covalent bonds between atoms. The bonding, called metallic bonding, results from the fact that the valence electrons are delocalized throughout the entire solid. That is, the valence electrons are not associated with specific atoms or bonds but are spread throughout the solid. In fact, we can visualize a metal as an array of positive ions immersed in a “sea” of delocalized valence electrons.
You have probably held a length of copper wire or an iron bolt. Perhaps you have even seen the surface of a freshly cut piece of sodium metal. These substances, although distinct from one another, share certain similarities that enable us to classify them as metallic. A clean metal surface has a characteristic luster. In addition, metals that we can handle with bare hands have a characteristic cold feeling related to their high thermal conductivity. Metals also have high electrical conductivity, which means that electrically charged particles flow easily through them. The thermal conductivity of a metal usually parallels its electrical conductivity. Silver and copper, for example, which possess the highest electrical conductivities among the elements, also possess the highest thermal conductivities.
Most metals are malleable, which means that they can be hammered into thin sheets, and ductile, which means that they can be drawn into wires (
FIGURE 12.10). These properties indicate that the atoms are capable of slipping past one another. Ionic and covalent-network solids do not exhibit such behavior. They are typically brittle and fracture easily. Consider, for example, the difference between dropping a ceramic plate and an aluminum cooking pan onto a concrete floor.
FIGURE 12.10 Malleability and ductility. Gold leaf demonstrates the characteristic malleability of metals, and copper wire demonstrates their ductility.
The Structures of Metallic Solids
The crystal structures of many metals are simple enough that we can generate the structure by placing a single atom on each lattice point. The structures corresponding to the three cubic lattices are shown in 
FIGURE 12.11. Metals with a primitive cubic structure are rare, one of the few examples being the radioactive element polonium. Body-centered cubic metals include iron, chromium, sodium, and tungsten. Examples of face-centered cubic metals include aluminum, lead, copper, silver, and gold.
Notice in the bottom row of Figure 12.11 that the atoms on the corners and faces of a unit cell do not lie wholly within the unit cell. These corner and face atoms are shared by neighboring unit cells. Because a cube has eight corners, each primitive cubic unit cell contains (1/8) × 8 = 1 atom, as shown in 
FIGURE 12.12 (a). Similarly, each body-centered cubic unit cell [Figure 12.12(b)] contains two atoms, (1/8) × 8 = 1 from the corners and 1 at the center of the unit cell. Atoms that lie on the face of a unit cell, as they do in a face-centered cubic metal, are shared by two unit cells so that only one-half of the atom belongs to each unit cell. Therefore, a face-centered cubic unit cell [Figure 12.12(c)] contains four atoms, (1/8) × 8 = 1 atom from the corners and (1/2) × 6 = 3 atoms from the faces.
FIGURE 12.11 The structures of (a) primitive cubic, (b) body-centered cubic, and (c) face-centered cubic metals. Each structure can be generated by the combination of a single-atom motif and the appropriate lattice.
TABLE 12.1 summarizes how the fractional part of each atom that resides within a unit cell depends on the atom's location in the cell.
TABLE 12.1 • Fraction of Any Atom as a Function of Location Within the Unit Cell*
* It is only the position of the center of the atom that matters. Atoms that reside near the boundary of the unit cell but not on a corner, edge, or face are counted as residing 100% within the unit cell.
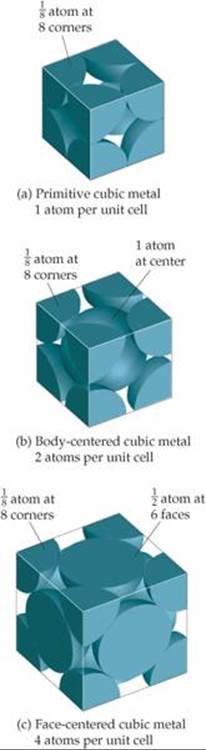
FIGURE 12.12 A space-filling view of unit cells for metals with a cubic structure. Only the portion of each atom that falls within the unit cell is shown.
Close Packing
The shortage of valence electrons and the fact that they are collectively shared make it favorable for the atoms in a metal to pack together closely. Because atoms are spherical objects, we can understand the structures of metals by considering how spheres pack. The most efficient way to pack one layer of equal-sized spheres is to surround each sphere by six neighbors, as shown at the top of FIGURE 12.13. To form a three-dimensional structure, we need to stack additional layers on top of this base layer. To maximize packing efficiency the second layer of spheres must sit in the depressions formed by the spheres in the first layer. If we start by placing an atom in the depression marked b1, the remaining spheres will fill all of the depressions marked with yellow dots. If we were to first fill the depression marked with a c1, all of the depressions marked with red dots would be filled. It's important to realize that the spheres are too large to simultaneously fill both sets of depressions. For the sake of discussion we arbitrarily put the second layer in the depressions marked with yellow dots.
For the third layer, we have two choices for where to place the spheres. One possibility is to put the third layer in the depressions that lie directly over the spheres in the first layer. This is done on the left-hand side of Figure 12.13, as shown by the dashed red lines in the side view. Continuing with this pattern, the fourth layer would lie directly over the spheres in the second layer, leading to the ABAB ... stacking shown on the left. This type of stacking is called hexagonal close packing (hcp). Alternatively, the third-layer spheres could lie directly over the depressions that were marked with red dots in the first layer. In this arrangement the spheres in the third layer do not sit directly above the spheres in either of the first two layers, as shown by the dashed red lines on the lower right hand side of Figure 12.13. Subsequent layers repeat this sequence to give the ABCABC ... stacking pattern shown on the right. This type of stacking is called cubic close packing (ccp). In both hexagonal close packing and cubic close packing, each sphere has 12 equidistant nearest neighbors: six neighbors in the same layer, three from the layer above, and three from the layer below. We say that each sphere has a coordination number of 12. The coordination number is the number of atoms immediately surrounding a given atom in a crystal structure.
GO FIGURE
What type of two-dimensional lattice describes the structure of a single layer of close-packed atoms?
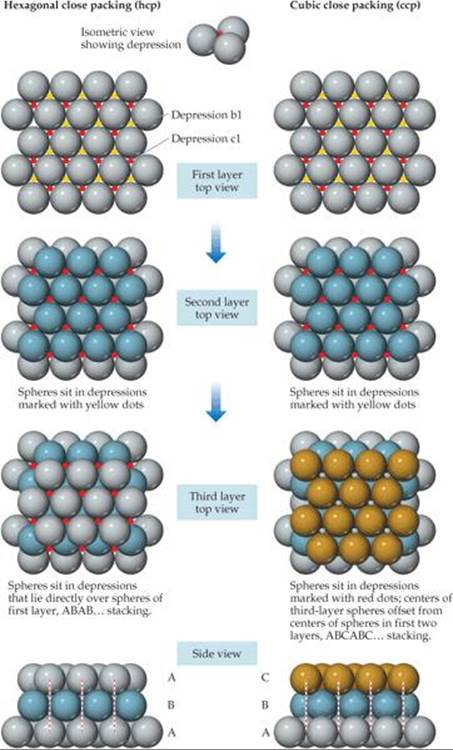
FIGURE 12.13 Close packing of equal-sized spheres. Hexagonal (left) close packing and cubic (right) close packing are equally efficient ways of packing spheres.
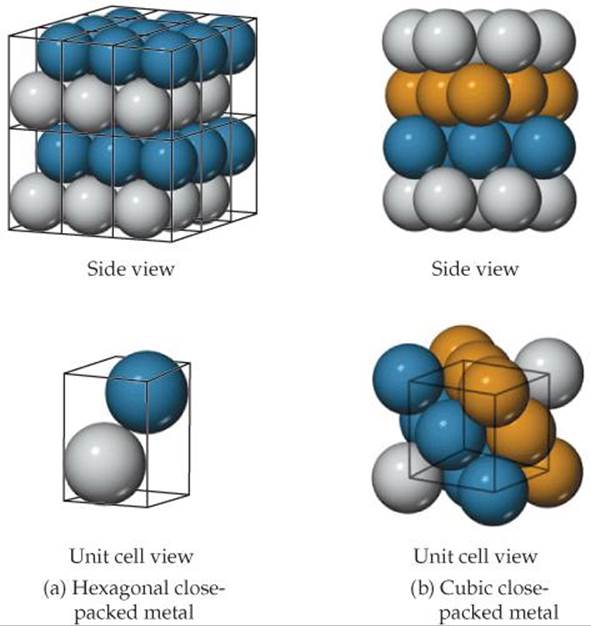
FIGURE 12.14 The unit cells for (a) a hexagonal close-packed metal and (b) a cubic close-packed metal. The solid lines indicate the unit cell boundaries.
The extended structure of a hexagonal close-packed metal is shown in 
FIGURE 12.14 (a). There are two atoms in the primitive hexagonal unit cell, one from each layer. Neither atom sits directly on the lattice points, which are located at the corners of the unit cell. The presence of two atoms in the unit cell is consistent with the two-layer ABAB ... stacking sequence associated with hcp packing.
Although it is not immediately obvious, the structure that results from cubic close packing possesses a unit cell that is identical to the face-centered cubic unit cell we encountered earlier [Figure 12.11(c)]. The relationship between the ABC ... layer stacking and the face-centered cubic unit cell is shown in Figure 12.14(b). In this figure we see that the layers stack perpendicular to the body diagonal of the cubic unit cell.
GIVE IT SOME THOUGHT
For metallic structures, does the packing efficiency (see Sample Exercise 12.1) increase or decrease as the number of nearest neighbors (the coordination number) decreases?
SAMPLE EXERCISE 12.1 Calculating Packing Efficiency
It is not possible to pack spheres together without leaving some void spaces between the spheres. Packing efficiency is the fraction of space in a crystal that is actually occupied by atoms. Determine the packing efficiency of a face-centered cubic metal.
SOLUTION
Analyze We must determine the volume taken up by the atoms that reside in the unit cell and divide this number by the volume of the unit cell.
Plan We can calculate the volume taken up by atoms by multiplying the number of atoms per unit cell by the volume of a sphere, 4πr3/3. To determine the volume of the unit cell, we must first identify the direction along which the atoms touch each other. We can then use geometry to express the length of the cubic unit cell edge, a, in terms of the radius of the atoms. Once we know the edge length, the cell volume is simply a3.
Solve As shown in Figure 12.12, a face-centered cubic metal has four atoms per unit cell. Therefore, the volume occupied by the atoms is
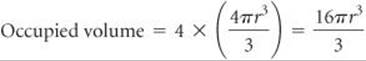
For a face-centered cubic metal the atoms touch along the diagonal of a face of the unit cell:
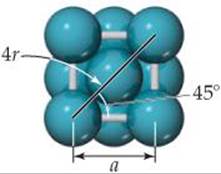
Therefore, a diagonal across a face of the unit cell is equal to 4 times the atomic radius, r. Using simple trigonometry, and the identity 
, we can show that
Finally, we calculate the packing efficiency by dividing the volume occupied by atoms by the volume of the cubic unit cell, a3:
PRACTICE EXERCISE
Determine the packing efficiency by calculating the fraction of space occupied by atoms in a body-centered cubic metal.
Answer: 0.68 or 68%
Alloys
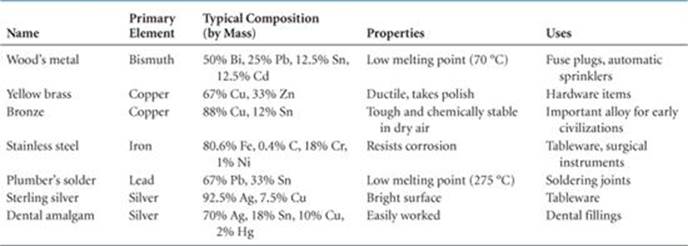
An alloy is a material that contains more than one element and has the characteristic properties of a metal. The alloying of metals is of great importance because it is one of the primary ways of modifying the properties of pure metallic elements. Nearly all the common uses of iron, for example, involve alloy compositions. Bronze is formed by alloying copper and tin, while brass is an alloy of copper and zinc. Pure gold is too soft to be used in jewelry, but alloys of gold are much harder (see “Chemistry Put to Work Box: Alloys of Gold”). Other common alloys are described in TABLE 12.2.
TABLE 12.2 • Some Common Alloys
GO FIGURE
What determines which species in a solid solution is the solute and which is the solvent?
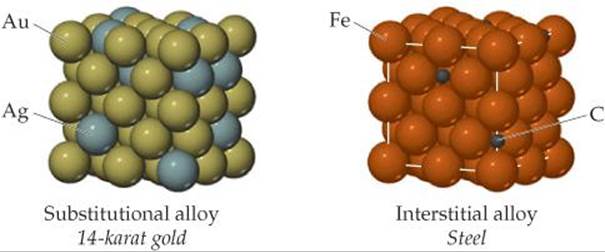
FIGURE 12.15 The distribution of solute and solvent atoms in a substitutional alloy and an interstitial alloy. Both types of alloys are solid solutions and, therefore, homogeneous mixtures.
Alloys can be divided into four categories: substitutional alloys, interstitial alloys, heterogeneous alloys, and intermetallic compounds. Substitutional and interstitial alloys are both homogeneous mixtures in which components are dispersed randomly and uniformly (FIGURE 12.15). 
(Section 1.2) Solids that form homogeneous mixtures are called solid solutions. When atoms of the solute in a solid solution occupy positions normally occupied by a solvent atom, we have a substitutional alloy. When the solute atoms occupy interstitial positions in the “holes” between solvent atoms, we have an interstitial alloy (Figure 12.15).
Substitutional alloys are formed when the two metallic components have similar atomic radii and chemical-bonding characteristics. For example, silver and gold form such an alloy over the entire range of possible compositions. When two metals differ in radii by more than about 15%, solubility is generally more limited.
For an interstitial alloy to form, the solute atoms must have a much smaller bonding atomic radius than the solvent atoms. Typically, the interstitial element is a nonmetal that makes covalent bonds to the neighboring metal atoms. The presence of the extra bonds provided by the interstitial component causes the metal lattice to become harder, stronger, and less ductile. For example, steel, which is much harder and stronger than pure iron, is an alloy of iron that contains up to 3% carbon. Mild steels contain less than 0.2% carbon; they are malleable and ductile and are used to make cables, nails, and chains. Medium steels contain 0.2-0.6% carbon; they are tougher than mild steels and are used to make girders and rails. High-carbon steel, used in cutlery, tools, and springs, contains 0.6-1.5% carbon. In all three types, other elements may be added to formalloy steels. Vanadium and chromium may be added to impart strength, for instance, and to increase resistance to fatigue and corrosion.
GIVE IT SOME THOUGHT
Would you expect the alloy PdB0.15 to be a substitutional alloy or an interstitial alloy?
One of the most important iron alloys is stainless steel, which contains about 0.4% carbon, 18% chromium, and 1% nickel. The chromium is obtained by carbon reduction of chromite (FeCr2O4) in an electric furnace. The product of the reduction is ferrochrome (FeCr2), which is added in the appropriate amount to molten iron to achieve the desired steel composition. The ratio of elements present in the steel may vary over a wide range, imparting a variety of specific physical and chemical properties to the materials.
FIGURE 12.16 Microscopic view of the structure of the heterogeneous alloy pearlite. The dark regions are body-centered cubic iron metal, and the lighter regions are cementite, Fe3C.
In a heterogeneous alloy the components are not dispersed uniformly. For example, the heterogeneous alloy pearlite contains two phases (FIGURE 12.16). One phase is essentially pure body-centered cubic iron, and the other is the compound Fe3C, known as cementite. In general, the properties of heterogeneous alloys depend on both the composition and the manner in which the solid is formed from the molten mixture. The properties of a heterogeneous alloy formed by rapid cooling of a molten mixture, for example, are distinctly different from the properties of an alloy formed by slow cooling of the same mixture.
Intermetallic compounds are compounds rather than mixtures. Because they are compounds, they have definite properties and their composition cannot be varied. Unlike the atoms in substitutional and interstitial alloys, the different types of atoms in an intermetallic compound are ordered rather than randomly distributed. The ordering of atoms in an intermetallic compound generally leads to better structural stability and higher melting points than what is observed in the constituent metals. These features can be attractive for high-temperature applications. On the negative side, intermetallic compounds are often more brittle than substitutional alloys.
Intermetallic compounds play many important roles in modern society. The intermetallic compound Ni3Al is a major component of jet aircraft engines because of its strength at high temperature and its low density. Razor blades are often coated with Cr3Pt, which adds hardness, allowing the blade to stay sharp longer. Both compounds have the structure shown on the left hand side of FIGURE 12.17. The compound Nb3Sn, also shown in Figure 12.17, is a superconductor, a substance that, when cooled below a critical temperature, conducts electricity with no resistance. In the case of Nb3Sn superconductivity is observed only when the temperature falls below 18 K. Superconductors are used in the magnets in MRI scanners widely employed for medical imaging. The need to keep the magnets cooled to such a low temperature is part of the reason why MRI devices are expensive to operate. The hexagonal intermetallic compound SmCo5, shown on the right hand side of Figure 12.17, is used to make the permanent magnets found in lightweight headsets and high-fidelity speakers. A related compound with the same structure, LaNi5, is used as the anode in nickel-metal hydride batteries.
GO FIGURE
In the unit cell drawing on the right, why do we see eight Sm atoms and nine Co atoms if the empirical formula is SmCo5?
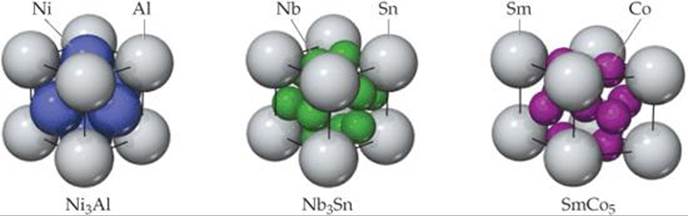
FIGURE 12.17 Three examples of intermetallic compounds.
CHEMISTRY PUT TO WORK
Alloys of Gold
Gold has long been a metal of choice for decorative objects, jewelry, and coins. The popularity of gold is driven by its unusual color (for a metal), its resistance to many chemical reactions, and the fact that it can easily be worked. However, pure gold is too soft for many applications, including jewelry. To increase its strength and hardness, as well as to modify its color, gold is often alloyed with other metals. In the jewelry trade pure gold is termed 24 karat. The karat number decreases as the mass percent of gold decreases. The most common alloys used in jewelry are 14 karat, which is (14/24) × 100 = 58% gold, and 18 karat, which is (18/24) × 100 = 75% gold. As an example of how alloying changes a metal's properties, an alloy that is 75% Au, 12.5% Ag, and 12.5% Cu (marked with the blue dot in Figure 12.18) has a tensile strength that is more than 10 times higher than that of pure gold and is more than 7 times harder than pure gold.
The color of gold varies depending on the metals it is alloyed with. Gold is typically alloyed with silver and/or copper. All three elements crystallize with a face-centered cubic structure. The fact that all three elements have similar radii (Au and Ag are nearly the same size, Cu is roughly 11% smaller) and crystallize with the same type of structure make it possible to form substitutional alloys with nearly any composition. The variations in color of these alloys as a function of composition are shown in FIGURE 12.18. Gold alloyed with equal parts silver and copper takes on the golden yellow color we associate with gold jewelry. Red or rose gold is a copper-rich alloy (
FIGURE 12.19). Silver-rich alloys take on a greenish hue, eventually giving way to silvery-white colors as silver becomes the majority constituent.
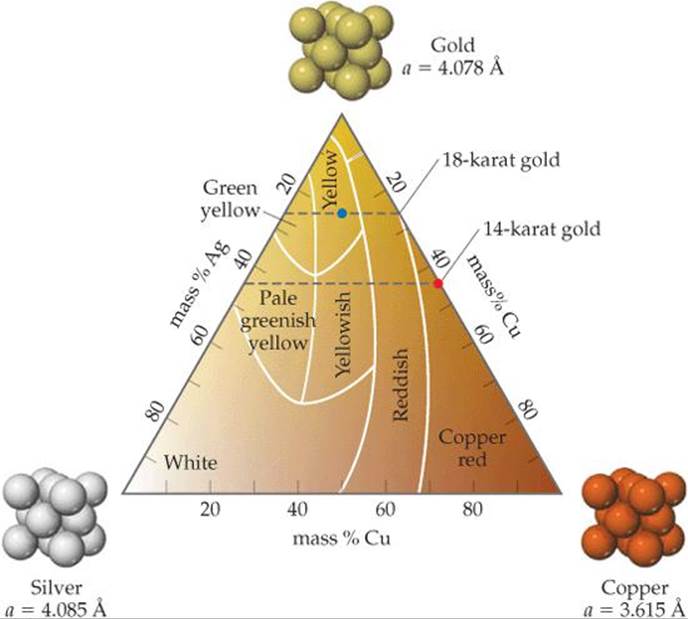
FIGURE 12.18 Colors of Au-Ag-Cu alloys as a function of composition.