CHEMISTRY THE CENTRAL SCIENCE
15 CHEMICAL EQUILIBRIUM
15.7 LE CHÂTELIER'S PRINCIPLE
Many of the products we use in everyday life are obtained from the chemical industry. Chemists and chemical engineers in industry spend a great deal of time and effort to maximize the yield of valuable products and minimize waste. For example, when Haber developed his process for making ammonia from N2 and H2, he examined how reaction conditions might be varied to increase yield. Using the values of the equilibrium constant at various temperatures, he calculated the equilibrium amounts of NH3 formed under a variety of conditions. Some of Haber's results are shown in ![]() FIGURE 15.9.
FIGURE 15.9.
![]() GO FIGURE
GO FIGURE
At what combination of pressure and temperature should you run the reaction to maximize NH3 yield?
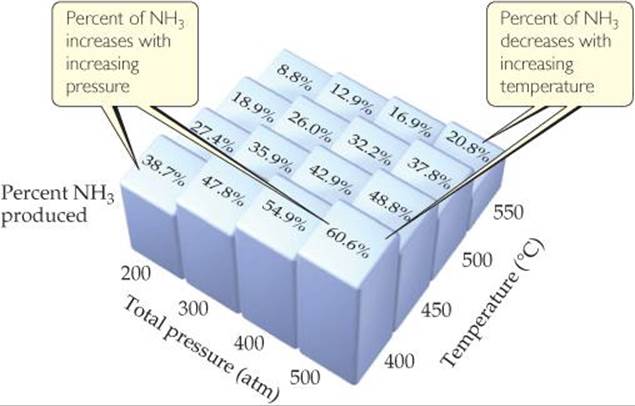
![]() FIGURE 15.9 Effect of temperature and pressure on NH3 yield in the Haber process. Each mixture was produced by starting with a 3:1 molar mixture of H2 and N2.
FIGURE 15.9 Effect of temperature and pressure on NH3 yield in the Haber process. Each mixture was produced by starting with a 3:1 molar mixture of H2 and N2.
Notice that the percent of NH3 present at equilibrium decreases with increasing temperature and increases with increasing pressure.
We can understand these effects in terms of a principle first put forward by Henri-Louis Le Châtelier* (1850–1936), a French industrial chemist: If a system at equilibrium is disturbed by a change in temperature, pressure, or a component concentration, the system will shift its equilibrium position so as to counteract the effect of the disturbance.
Le Chatelier's Principle
If a system at equilibrium is disturbed by a change in concentration, pressure, or temperature, the system will shift its equilibrium position so as to counter the effect of the disturbance.
Concentration: adding or removing a reactant or product
If a substance is added to a system at equilibrium, the system reacts to consume some of the substance. If a substance is removed from a system, the system reacts to produce more of substance.

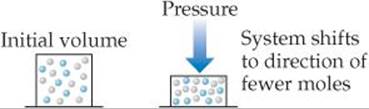
Pressure: changing the pressure by changing the volume
At constant temperature, reducing the volume of a gaseous equilibrium mixture causes the system to shift in the direction that reduces the number of moles of gas.
Temperature:
If the temperature of a system at equilibrium is increased, the system reacts as if we added a reactant to an endothermic reaction or a product to an exothermic reaction. The equilibrium shifts in the direction that consumes the “excess reactant,” namely heat.


In this section we use Le Châtelier's principle to make qualitative predictions about how a system at equilibrium responds to various changes in external conditions. We consider three ways in which a chemical equilibrium can be disturbed: (1) adding or removing a reactant or product, (2) changing the pressure by changing the volume, and (3) changing the temperature.
Change in Reactant or Product Concentration
A system at dynamic equilibrium is in a state of balance. When the concentrations of species in the reaction are altered, the equilibrium shifts until a new state of balance is attained. What does shift mean? It means that reactant and product concentrations change over time to accommodate the new situation. Shift does not mean that the equilibrium constant itself is altered; the equilibrium constant remains the same. Le Châtelier's principle states that the shift is in the direction that minimizes or reduces the effect of the change. Therefore, if a chemical system is already at equilibrium and the concentration of any substance in the mixture is increased (either reactant or product), the system reacts to consume some of that substance. Conversely, if the concentration of a substance is decreased, the system reacts to produce some of that substance.
There is no change in the equilibrium constant when we change the concentrations of reactants or products. As an example, consider our familiar equilibrium mixture of N2, H2, and NH3:
![]()
Adding H2 causes the system to shift so as to reduce the increased concentration of H2 (![]() FIGURE 15.10). This change can occur only if the reaction consumes H2 and simultaneously consumes N2 to form more NH3. Adding N2 to the equilibrium mixture likewise causes the reaction to shift toward forming more NH3. Removing NH3 also causes a shift toward producing more NH3, whereas adding NH3 to the system at equilibrium causes the reaction to shift in the direction that reduces the increased NH3 concentration: Some of the added ammonia decomposes to form N2 and H2.
FIGURE 15.10). This change can occur only if the reaction consumes H2 and simultaneously consumes N2 to form more NH3. Adding N2 to the equilibrium mixture likewise causes the reaction to shift toward forming more NH3. Removing NH3 also causes a shift toward producing more NH3, whereas adding NH3 to the system at equilibrium causes the reaction to shift in the direction that reduces the increased NH3 concentration: Some of the added ammonia decomposes to form N2 and H2.
In the Haber reaction, therefore, removing NH3 from an equilibrium mixture of N2, H2, and NH3 causes the reaction to shift right to form more NH3. If the NH3 can be removed continuously as it is produced, the yield can be increased dramatically. In the industrial production of ammonia, the NH3 is continuously removed by selectively liquefying it (![]() FIGURE 15.11). (The boiling point of NH3, –33 °C, is much higher than those of N2, –196 °C, and H2, –253 °C.) The liquid NH3 is removed, and the N2 and H2 are recycled to form more NH3. As a result of the product being continuously removed, the reaction is driven essentially to completion.
FIGURE 15.11). (The boiling point of NH3, –33 °C, is much higher than those of N2, –196 °C, and H2, –253 °C.) The liquid NH3 is removed, and the N2 and H2 are recycled to form more NH3. As a result of the product being continuously removed, the reaction is driven essentially to completion.
![]() GO FIGURE
GO FIGURE
Why does the nitrogen concentration decrease after hydrogen is added?
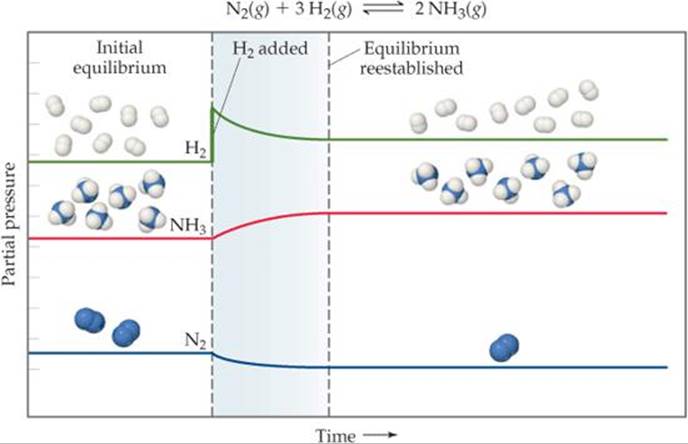
![]() FIGURE 15.10 Effect of adding H2 to an equilibrium mixture of N2, H2, and NH3. Adding H2 causes the reaction as written to shift to the right, consuming some H2 to produce more NH3.
FIGURE 15.10 Effect of adding H2 to an equilibrium mixture of N2, H2, and NH3. Adding H2 causes the reaction as written to shift to the right, consuming some H2 to produce more NH3.
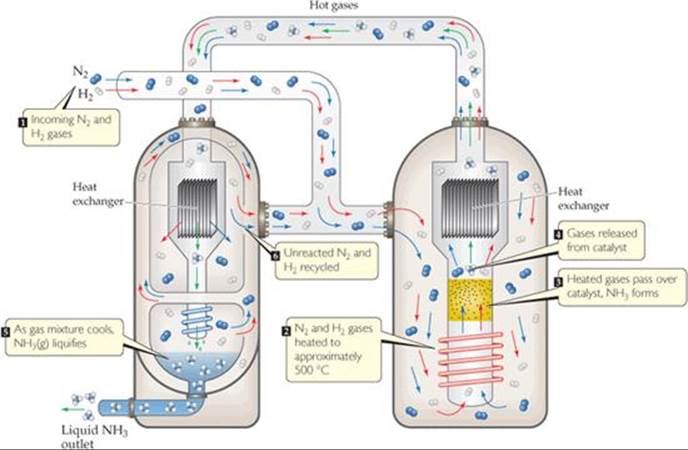
![]() FIGURE 15.11 Diagram of the industrial production of ammonia. Incoming N2(g) and H2(g) are heated to approximately 500 °C and passed over a catalyst. When the resultant N2, H2, and NH3 mixture is cooled, the NH3 liquefies and is removed from the mixture, shifting the reaction to produce more NH3.
FIGURE 15.11 Diagram of the industrial production of ammonia. Incoming N2(g) and H2(g) are heated to approximately 500 °C and passed over a catalyst. When the resultant N2, H2, and NH3 mixture is cooled, the NH3 liquefies and is removed from the mixture, shifting the reaction to produce more NH3.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
What happens to the equilibrium 2 NO(g) + O2(g) ![]() 2 NO2(g) if
2 NO2(g) if
a. O2 is added to the system,
b. NO is removed?
Effects of Volume and Pressure Changes
If a system containing one or more gases is at equilibrium and its volume is decreased, thereby increasing its total pressure, Le Châtelier's principle indicates that the system responds by shifting its equilibrium position to reduce the pressure. A system can reduce its pressure by reducing the total number of gas molecules (fewer molecules of gas exert a lower pressure). Thus, at constant temperature, reducing the volume of a gaseous equilibrium mixture causes the system to shift in the direction that reduces the number of moles of gas. Increasing the volume causes a shift in the direction that produces more gas molecules (![]() FIGURE 15.12).
FIGURE 15.12).
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
What happens to the equilibrium 2 SO2(g) + O2(g) ![]() 2 SO3(g) if the volume of the system is increased?
2 SO3(g) if the volume of the system is increased?
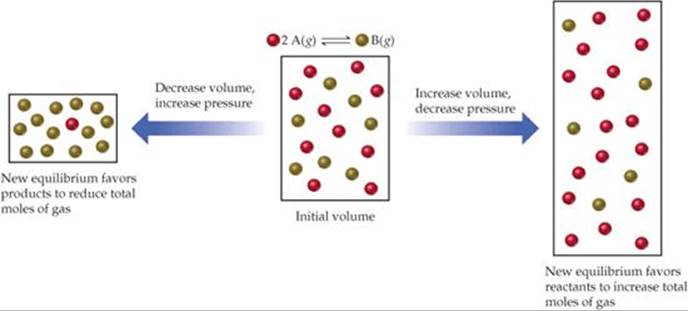
![]() FIGURE 15.12 Pressure and Le Châtelier's principle.
FIGURE 15.12 Pressure and Le Châtelier's principle.
In the reaction N2(g) + 3 H2(g) ![]() 2 NH3(g), four molecules of reactant are consumed for every two molecules of product produced. Consequently, an increase in pressure (caused by a decrease in volume) shifts the reaction in the direction that produces fewer gas molecules, which leads to the formation of more NH3, as indicated in Figure 15.9. In the reaction H2(g) + I2(g)
2 NH3(g), four molecules of reactant are consumed for every two molecules of product produced. Consequently, an increase in pressure (caused by a decrease in volume) shifts the reaction in the direction that produces fewer gas molecules, which leads to the formation of more NH3, as indicated in Figure 15.9. In the reaction H2(g) + I2(g) ![]() 2 HI(g), the number of molecules of gaseous products (two) equals the number of molecules of gaseous reactants; therefore, changing the pressure does not influence the position of equilibrium.
2 HI(g), the number of molecules of gaseous products (two) equals the number of molecules of gaseous reactants; therefore, changing the pressure does not influence the position of equilibrium.
Keep in mind that, as long as temperature remains constant, pressure-volume changes do not change the value of K. Rather, these changes alter the partial pressures of the gaseous substances. In Sample Exercise 15.8, we calculated Kp = 2.79 × 10–5 for the Haber reaction, N2(g) + 3 H2(g) ![]() 2 NH3(g), in an equilibrium mixture at 472 °C containing 7.38 atm H2, 2.46 atm N2, and 0.166 atm NH3. Consider what happens when we suddenly reduce the volume of the system by one-half. If there were no shift in equilibrium, this volume change would cause the partial pressures of all substances to double, giving PH2 = 14.76 atm, PN2 = 4.92 atm, and PNH3 = 0.332 atm. The reaction quotient would then no longer equal the equilibrium constant:
2 NH3(g), in an equilibrium mixture at 472 °C containing 7.38 atm H2, 2.46 atm N2, and 0.166 atm NH3. Consider what happens when we suddenly reduce the volume of the system by one-half. If there were no shift in equilibrium, this volume change would cause the partial pressures of all substances to double, giving PH2 = 14.76 atm, PN2 = 4.92 atm, and PNH3 = 0.332 atm. The reaction quotient would then no longer equal the equilibrium constant:

Because Qp < Kp, the system would no longer be at equilibrium. Equilibrium would be reestablished by increasing PNH3 and/or decreasing PN2 and PH2 until Qp= Kp= 2.79 × 10–5. Therefore, the equilibrium shifts to the right in the reaction as written, as Le Châtelier's principle predicts.
It is possible to change the pressure of a system in which a chemical reaction is running without changing its volume. For example, pressure increases if additional amounts of any reacting components are added to the system. We have already seen how to deal with a change in concentration of a reactant or product. The total pressure in the reaction vessel might also be increased by adding a gas that is not involved in the equilibrium. For example, argon might be added to the ammonia equilibrium system. The argon would not alter the partial pressures of any of the reacting components and therefore would not cause a shift in equilibrium.
Effect of Temperature Changes
Changes in concentrations or partial pressures shift equilibria without changing the value of the equilibrium constant. In contrast, almost every equilibrium constant changes as the temperature changes. For example, consider the equilibrium established when cobalt(II) chloride (CoCl2) is dissolved in hydrochloric acid, HCl(aq), in the en-dothermic reaction
![]()
Because Co(H2O)62+ is pink and CoCl42– is blue, the position of this equilibrium is readily apparent from the color of the solution (![]() FIGURE 15.13). When the solution is heated it turns blue, indicating that the equilibrium has shifted to form more CoCl42–. Cooling the solution leads to a pink solution, indicating that the equilibrium has shifted to produce more Co(H2O)62+. We can monitor this reaction by spectroscopic methods, measuring the concentration of all species at the different temperatures.
FIGURE 15.13). When the solution is heated it turns blue, indicating that the equilibrium has shifted to form more CoCl42–. Cooling the solution leads to a pink solution, indicating that the equilibrium has shifted to produce more Co(H2O)62+. We can monitor this reaction by spectroscopic methods, measuring the concentration of all species at the different temperatures. ![]() (Section 14.2) We can then calculate the equilibrium constant at each temperature. How can we explain the fact that the equilibrium constants and therefore the position of equilibrium both depend on temperature?
(Section 14.2) We can then calculate the equilibrium constant at each temperature. How can we explain the fact that the equilibrium constants and therefore the position of equilibrium both depend on temperature?
We can deduce the rules for the relationship between K and temperature from Le Châtelier's principle. We do this by treating heat as a chemical reagent. In an endothermic (heat-absorbing) reaction, we consider heat a reactant, and in an exothermic (heat-releasing) reaction, we consider heat a product:
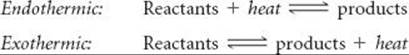
When the temperature of a system at equilibrium is increased, the system reacts as if we added a reactant to an endothermic reaction or a product to an exothermic reaction. The equilibrium shifts in the direction that consumes the excess reactant (or product), namely heat.
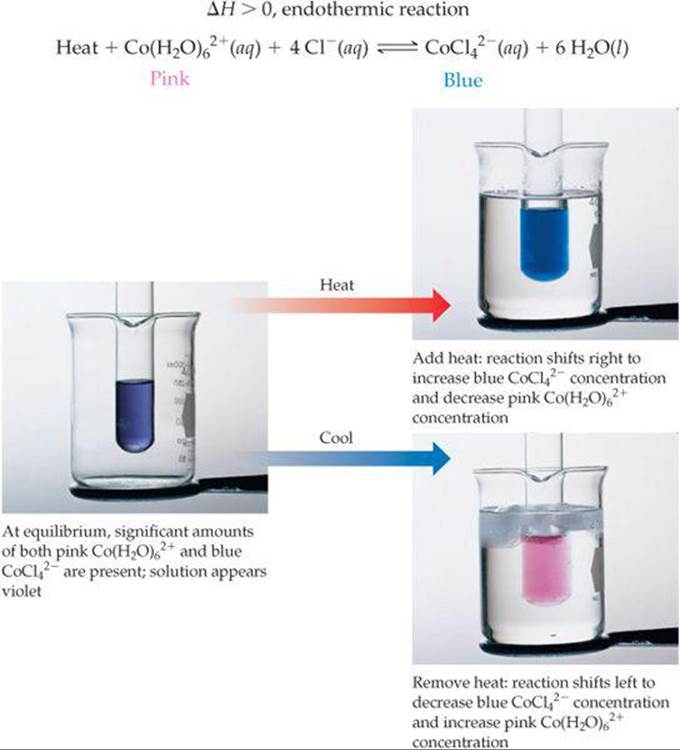
![]() FIGURE 15.13 Temperature and Le Châtelier's principle.
FIGURE 15.13 Temperature and Le Châtelier's principle.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
Use Le Châtelier's principle to explain why the equilibrium vapor pressure of a liquid increases with increasing temperature.
In an endothermic reaction, such as Equation 15.24, heat is absorbed as reactants are converted to products. Thus, increasing the temperature causes the equilibrium to shift to the right, in the direction of making more products, and K increases. In an exothermic reaction, the opposite occurs: Heat is produced as reactants are converted to products. Thus, increasing the temperature in this case causes the equilibrium to shift to the left, in the direction of making more reactants, and K decreases.

Cooling a reaction has the opposite effect. As we lower the temperature, the equilibrium shifts in the direction that produces heat. Thus, cooling an endothermic reaction shifts the equilibrium to the left, decreasing K, as shown in Figure 15.13, and cooling an exothermic reaction shifts the equilibrium to the right, increasing K.
SAMPLE EXERCISE 15.13 Using Le Châtelier's Principle to Predict Shifts in Equilibrium
Consider the equilibrium
![]()
In which direction will the equilibrium shift when (a) N2O4 is added, (b) NO2 is removed, (c) the pressure is increased by addition of N2(g), (d) the volume is increased, (e) the temperature is decreased?
SOLUTION
Analyze We are given a series of changes to be made to a system at equilibrium and are asked to predict what effect each change will have on the position of the equilibrium.
Plan Le Châtelier's principle can be used to determine the effects of each of these changes.
Solve
(a) The system will adjust to decrease the concentration of the added N2O4, so the equilibrium shifts to the right, in the direction of product.
(b) The system will adjust to the removal of NO2 by shifting to the side that produces more NO2; thus, the equilibrium shifts to the right.
(c) Adding N2 will increase the total pressure of the system, but N2 is not involved in the reaction. The partial pressures of NO2 and N2O4 are therefore unchanged, and there is no shift in the position of the equilibrium.
(d) If the volume is increased, the system will shift in the direction that occupies a larger volume (more gas molecules); thus, the equilibrium shifts to the right.
(e) The reaction is endothermic, so we can imagine heat as a reagent on the reactant side of the equation. Decreasing the temperature will shift the equilibrium in the direction that produces heat, so the equilibrium shifts to the left, toward the formation of more N2O4. Note that only this last change also affects the value of the equilibrium constant, K.
PRACTICE EXERCISE
For the reaction
![]()
in which direction will the equilibrium shift when (a) Cl2(g) is removed, (b) the temperature is decreased, (c) the volume of the reaction system is increased, (d) PCl3(g) is added?
Answers: (a) right, (b) left, (c) right, (d) left
SAMPLE EXERCISE 15.14 Predicting the Effect of Temperature on K
(a) Using the standard heat of formation data in Appendix C, determine the standard enthalpy change for the reaction
![]()
(b) Determine how the equilibrium constant for this reaction should change with temperature.
SOLUTION
Analyze We are asked to determine the standard enthalpy change of a reaction and how the equilibrium constant for the reaction varies with temperature.
Plan (a) We can use standard enthalpies of formation to calculate ΔH° for the reaction. (b) We can then use Le Châtelier's principle to determine what effect temperature will have on the equilibrium constant.
Solve
(a) Recall that the standard enthalpy change for a reaction is given by the sum of the standard molar enthalpies of formation of the products, each multiplied by its coefficient in the balanced chemical equation, less the same quantities for the reactants. ![]() (Section 5.7) At 25 °C,
(Section 5.7) At 25 °C, ![]() for NH3(g) is –46.19 kJ/mol. The
for NH3(g) is –46.19 kJ/mol. The ![]() values for H2(g) and N2(g) are zero by definition because the enthalpies of formation of the elements in their normal states at 25 °C are defined as zero.
values for H2(g) and N2(g) are zero by definition because the enthalpies of formation of the elements in their normal states at 25 °C are defined as zero. ![]() (Section 5.7) Because 2 mol of NH3 is formed, the total enthalpy change is
(Section 5.7) Because 2 mol of NH3 is formed, the total enthalpy change is
![]()
(b) Because the reaction in the forward direction is exothermic, we can consider heat a product of the reaction. An increase in temperature causes the reaction to shift in the direction of less NH3 and more N2 and H2. This effect is seen in the values for Kp presented in ![]() TABLE 15.2. Notice that Kp changes markedly with changes in temperature and that it is larger at lower temperatures.
TABLE 15.2. Notice that Kp changes markedly with changes in temperature and that it is larger at lower temperatures.
TABLE 15.2 • Variation in Kp with Temperature for N2 + 3 H2 ![]() 2 NH3
2 NH3
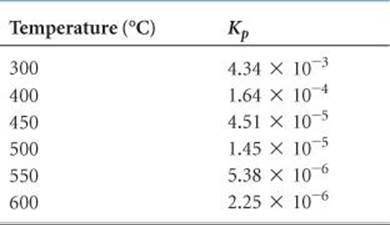
Comment The fact that Kp for the formation of NH3 from N2 and H2 decreases with increasing temperature is a matter of great practical importance. To form NH3 at a reasonable rate requires higher temperatures. At higher temperatures, however, the equilibrium constant is smaller, and so the percentage conversion to NH3 is smaller. To compensate for this, higher pressures are needed because high pressure favors NH3 formation.
PRACTICE EXERCISE
Using the thermodynamic data in Appendix C, determine the enthalpy change for the reaction
![]()
Use this result to determine how the equilibrium constant for the reaction should change with temperature.
Answer: ΔH° = 508.3 kJ; the equilibrium constant will increase with increasing temperature
The Effect of Catalysts
What happens if we add a catalyst to a chemical system that is at equilibrium? As shown in ![]() FIGURE 15.14,
FIGURE 15.14, ![]() (Figure 14.23) a catalyst lowers the activation barrier between reactants and products. The activation energies for both the forward and reverse reactions are lowered. The catalyst thereby increases the rates of both forward and reverse reactions. Since K is the ratio of the forward and reverse rate constants for a reaction, you can predict, correctly, that the presence of a catalyst, even though it changes the reaction rate, does not affect the numeric value of K(Figure 15.14). As a result, a catalyst increases the rate at which equilibrium is achieved but does not change the composition of the equilibrium mixture.
(Figure 14.23) a catalyst lowers the activation barrier between reactants and products. The activation energies for both the forward and reverse reactions are lowered. The catalyst thereby increases the rates of both forward and reverse reactions. Since K is the ratio of the forward and reverse rate constants for a reaction, you can predict, correctly, that the presence of a catalyst, even though it changes the reaction rate, does not affect the numeric value of K(Figure 15.14). As a result, a catalyst increases the rate at which equilibrium is achieved but does not change the composition of the equilibrium mixture.
The rate at which a reaction approaches equilibrium is an important practical consideration. As an example, let's again consider the synthesis of ammonia from N2 and H2. In designing his process, Haber had to deal with a rapid decrease in the equilibrium constant with increasing temperature (Table 15.2). At temperatures sufficiently high to give a satisfactory reaction rate, the amount of ammonia formed was too small. The solution to this dilemma was to develop a catalyst that would produce a reasonably rapid approach to equilibrium at a sufficiently low temperature, so that the equilibrium constant remained reasonably large. The development of a suitable catalyst thus became the focus of Haber's research efforts.
![]() GO FIGURE
GO FIGURE
How much faster is the catalyzed reaction compared to the uncatalyzed reaction?
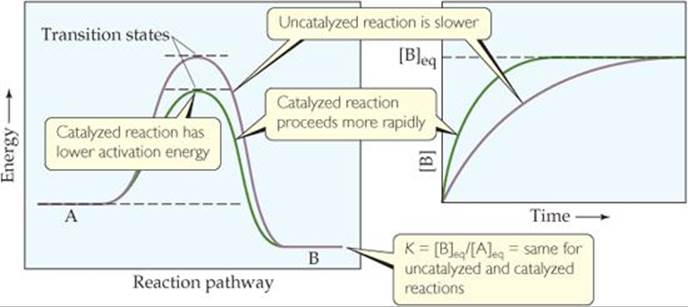
![]() FIGURE 15.14 A catalyst increases the rate at which equilibrium is reached but does not change the overall composition of the mixture at equilibrium.
FIGURE 15.14 A catalyst increases the rate at which equilibrium is reached but does not change the overall composition of the mixture at equilibrium.
After trying different substances to see which would be most effective, Carl Bosch (see “Chemistry Put to Work: The Haber Process,” page 615) settled on iron mixed with metal oxides, and variants of this catalyst formulation are still used today. These catalysts make it possible to obtain a reasonably rapid approach to equilibrium at around 400 to 500 °C and 200 to 600 atm. The high pressures are needed to obtain a satisfactory equilibrium amount of NH3. If chemists and chemical engineers could identify a catalyst that leads to sufficiently rapid reaction at temperatures lower than 400 °C, it would be possible to obtain the same extent of equilibrium conversion at pressures much lower than 200 to 600 atm. This would result in great savings in the cost of the high-pressure equipment used in ammonia synthesis today.
As noted in Section 15.2, our need for nitrogen as fertilizer is growing globally, making the fixation of nitrogen a process of ever-increasing importance.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
Does the addition of a catalyst have any effect on the position of an equilibrium?
SAMPLE INTEGRATIVE EXERCISE Putting Concepts Together
At temperatures near 800 °C, steam passed over hot coke (a form of carbon obtained from coal) reacts to form CO and H2:
![]()
The mixture of gases that results is an important industrial fuel called water gas. (a) At 800 °C the equilibrium constant for this reaction is Kp = 14.1. What are the equilibrium partial pressures of H2O, CO, and H2 in the equilibrium mixture at this temperature if we start with solid carbon and 0.100 mol of H2O in a 1.00-L vessel? (b) What is the minimum amount of carbon required to achieve equilibrium under these conditions? (c) What is the total pressure in the vessel at equilibrium? (d) At 25 °C the value of Kp for this reaction is 1.7 × 10–21. Is the reaction exothermic or endothermic? (e) To produce the maximum amount of CO and H2 at equilibrium, should the pressure of the system be increased or decreased?
SOLUTION
(a) To determine the equilibrium partial pressures, we use the ideal-gas equation, first determining the starting partial pressure of hydrogen.

We then construct a table of initial partial pressures and their changes as equilibrium is achieved:

There are no entries in the table under C(s) because the reactant, being a solid, does not appear in the equilibrium-constant expression. Substituting the equilibrium partial pressures of the other species into the equilibrium-constant expression for the reaction gives
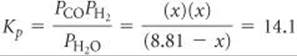
Multiplying through by the denominator gives a quadratic equation in x:
![]()
Solving this equation for x using the quadratic formula yields x = 6.14 atm. Hence, the equilibrium partial pressures are PCO = x = 6.14 atm, PH2 = x = 6.14 atm, and PH2O = (8.81 - x) = 2.67 atm.
(b) Part (a) shows that x = 6.14 atm of H2O must react for the system to achieve equilibrium. We can use the ideal-gas equation to convert this partial pressure into a mole amount.

Thus, 0.0697 mol of H2O and the same amount of C must react to achieve equilibrium. As a result, there must be at least 0.0697 mol of C (0.836 g C) present among the reactants at the start of the reaction.
(c) The total pressure in the vessel at equilibrium is simply the sum of the equilibrium partial pressures:
![]()
(d) In discussing Le Châtelier's principle, we saw that endothermic reactions exhibit an increase in Kp with increasing temperature. Because the equilibrium constant for this reaction increases as temperature increases, the reaction must be endothermic. From the enthalpies of formation given in Appendix C, we can verify our prediction by calculating the enthalpy change for the reaction, ΔH° = ![]() (CO(g)) +
(CO(g)) + ![]() (H2(g)) -
(H2(g)) - ![]() (C(s, graphite)) -
(C(s, graphite)) - ![]() (H2O(g)) = +131.3 KJ. The positive sign for ΔH° indicates that the reaction is endothermic.
(H2O(g)) = +131.3 KJ. The positive sign for ΔH° indicates that the reaction is endothermic.
(e) According to Le Châtelier's principle, a decrease in the pressure causes a gaseous equilibrium to shift toward the side of the equation with the greater number of moles of gas. In this case there are two moles of gas on the product side and only one on the reactant side. Therefore, the pressure should be decreased to maximize the yield of the CO and H2.
 CHEMISTRY PUT TO WORK
CHEMISTRY PUT TO WORK
Controlling Nitric Oxide Emissions
The formation of NO from N2 and O2,
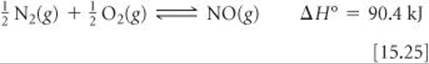
provides an interesting example of the practical importance of the fact that equilibrium constants and reaction rates change with temperature. By applying Le Châtelier's principle to this endothermic reaction and treating heat as a reactant, we deduce that an increase in temperature shifts the equilibrium in the direction of more NO. The equilibrium constant Kp for formation of 1 mol of NO from its elements at 300 K is only about 1 × 10–15 (![]() FIGURE 15.15). At 2400 K, however, the equilibrium constant is about 0.05, which is 10 times larger than the 300 K value.
FIGURE 15.15). At 2400 K, however, the equilibrium constant is about 0.05, which is 10 times larger than the 300 K value.
Figure 15.15 helps explain why NO is a pollution problem. In the cylinder of a modern high-compression automobile engine, the temperature during the fuel-burning part of the cycle is approximately 2400 K. Also, there is a fairly large excess of air in the cylinder. These conditions favor the formation of NO. After combustion, however, the gases cool quickly. As the temperature drops, the equilibrium in Equation 15.25 shifts to the left (because the reactant heat is being removed). The lower temperature also means that the reaction rate decreases, however, so the NO formed at 2400 K is essentially “frozen” in that form as the gas cools.
The gases exhausting from the cylinder are still quite hot, perhaps 1200 K. At this temperature, as shown in Figure 15.15, the equilibrium constant for formation of NO is about 5 × 10–4, much smaller than the value at 2400 K. However, the rate of conversion of NO to N2 and O2 is too slow to permit much loss of NO before the gases are cooled further.
As discussed in the “Chemistry Put to Work” box in Section 14.7, one of the goals of automotive catalytic converters is to achieve rapid conversion of NO to N2 and O2 at the temperature of the exhaust gas. Some catalysts developed for this reaction are reasonably effective under the grueling conditions in automotive exhaust systems. Nevertheless, scientists and engineers are continuously searching for new materials that provide even more effective catalysis of the decomposition of nitrogen oxides.
![]() GO FIGURE
GO FIGURE
Estimate the value of Kp at 1200 K, the exhaust gas temperature.
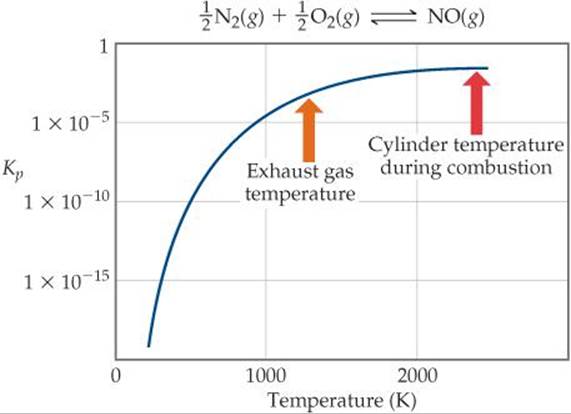
![]() FIGURE 15.15 Equilibrium and temperature. The equilibrium constant increases with increasing temperature because the reaction is endothermic. It is necessary to use a log scale for Kp because the values vary over such a large range.
FIGURE 15.15 Equilibrium and temperature. The equilibrium constant increases with increasing temperature because the reaction is endothermic. It is necessary to use a log scale for Kp because the values vary over such a large range.