CHEMISTRY THE CENTRAL SCIENCE
21 NUCLEAR CHEMISTRY
21.4 RATES OF RADIOACTIVE DECAY
Some radioisotopes, such as uranium-238, are found in nature even though they are not stable. Other radioisotopes do not exist in nature but can be synthesized in nuclear reactions. To understand this distinction, we must realize that different nuclei undergo radioactive decay at different rates. Many radioisotopes decay essentially completely in a matter of seconds, so we do not find them in nature. Uranium-238, on the other hand, decays very slowly. Therefore, despite its instability, we can still observe what remains from its formation in the early history of the universe.
Radioactive decay is a first-order kinetic process. Recall that a first-order process has a characteristic half-life, which is the time required for half of any given quantity of a substance to react. ![]() (Section 14.4) Nuclear decay rates are commonly expressed in terms of half-lives. Each isotope has its own characteristic half-life. For example, the half-life of strontium-90 is 28.8 yr (
(Section 14.4) Nuclear decay rates are commonly expressed in terms of half-lives. Each isotope has its own characteristic half-life. For example, the half-life of strontium-90 is 28.8 yr (![]() FIGURE 21.6). If we start with 10.0 g of strontium-90, only 5.0 g of that isotope remains after 28.8 yr, 2.5 g remains after another 28.8 yr, and so on. Strontium-90 decays to yttrium-90:
FIGURE 21.6). If we start with 10.0 g of strontium-90, only 5.0 g of that isotope remains after 28.8 yr, 2.5 g remains after another 28.8 yr, and so on. Strontium-90 decays to yttrium-90:
![]()
![]() GO FIGURE
GO FIGURE
If we start with a 50.0-g sample, how much of it remains after three half-lives have passed?
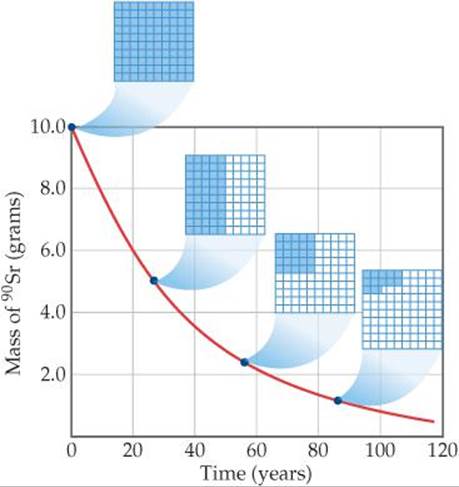
![]() FIGURE 21.6 Decay of a 10.0-g sample of strontium-90 (t1/2 = 28.8 yr). The 10 × 10 grids show how much of the radioactive isotope remains after various amounts of time.
FIGURE 21.6 Decay of a 10.0-g sample of strontium-90 (t1/2 = 28.8 yr). The 10 × 10 grids show how much of the radioactive isotope remains after various amounts of time.
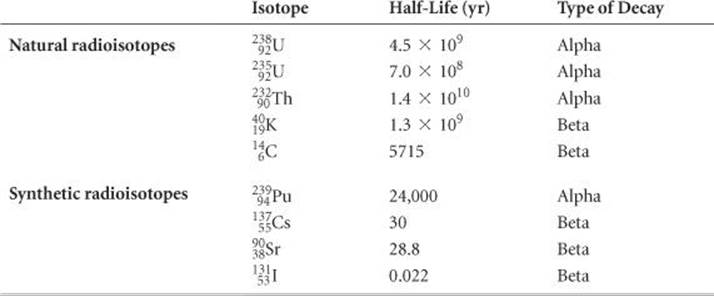
Half-lives as short as millionths of a second and as long as billions of years are known. The half-lives of some radioisotopes are listed in ![]() TABLE 21.5. One important feature of half-lives for nuclear decay is that they are unaffected by external conditions such as temperature, pressure, or state of chemical combination. Unlike toxic chemicals, therefore, radioactive atoms cannot be rendered harmless by chemical reaction or by any other practical treatment. At this point, we can do nothing but allow these nuclei to lose radioactivity at their characteristic rates. In the meantime, we must take precautions to prevent radioisotopes, such as those produced in nuclear power plants (Section 21.7), from entering the environment because of the damage radiation can cause.
TABLE 21.5. One important feature of half-lives for nuclear decay is that they are unaffected by external conditions such as temperature, pressure, or state of chemical combination. Unlike toxic chemicals, therefore, radioactive atoms cannot be rendered harmless by chemical reaction or by any other practical treatment. At this point, we can do nothing but allow these nuclei to lose radioactivity at their characteristic rates. In the meantime, we must take precautions to prevent radioisotopes, such as those produced in nuclear power plants (Section 21.7), from entering the environment because of the damage radiation can cause.
TABLE 21.5 • The Half-Lives and Type of Decay for Several Radioisotopes
SAMPLE EXERCISE 21.6 Calculation Involving Half-Lives
The half-life of cobalt-60 is 5.3 yr. How much of a 1.000-mg sample of cobalt-60 is left after 15.9 yr?
SOLUTION
Analyze We are given the half-life for cobalt-60 and asked to calculate the amount of cobalt-60 remaining from an initial 1.000-mg sample after 15.9 yr.
Plan We will use the fact that the amount of a radioactive substance decreases by 50% for every half-life that passes.
Solve Because 5.3 × 3 = 15.9, 15.9 yr is three half-lives for cobalt-60. At the end of one half-life, 0.500 mg of cobalt-60 remains, 0.250 mg at the end of two half-lives, and 0.125 mg at the end of three half-lives.
PRACTICE EXERCISE
Carbon-11, used in medical imaging, has a half-life of 20.4 min. The carbon-11 nuclides are formed, and the carbon atoms are then incorporated into an appropriate compound. The resulting sample is injected into a patient, and the medical image is obtained. If the entire process takes five half-lives, what percentage of the original carbon-11 remains at this time?
Answer: 3.12%
Radiometric Dating
Because the half-life of any particular nuclide is constant, the half-life can serve as a nuclear clock to determine the age of objects. The method of dating objects based on their isotopes and isotope abundances is called radiometric dating.
When carbon-14 is used in radiometric dating, the technique is known as radiocarbon dating. The procedure is based on the formation of carbon-14 as neutrons created by cosmic rays in the upper atmosphere convert nitrogen-14 into carbon-14 (![]() FIGURE 21.7). The 14C reacts with oxygen to form 14CO2 in the atmosphere, and this “labeled” CO2 is taken up by plants and introduced into the food chain through photosynthesis. This process provides a small but reasonably constant source of carbon-14, which is radioactive and undergoes beta decay with a half-life of 5715 yr:
FIGURE 21.7). The 14C reacts with oxygen to form 14CO2 in the atmosphere, and this “labeled” CO2 is taken up by plants and introduced into the food chain through photosynthesis. This process provides a small but reasonably constant source of carbon-14, which is radioactive and undergoes beta decay with a half-life of 5715 yr:
![]()
Because a living plant or animal has a constant intake of carbon compounds, it is able to maintain a ratio of carbon-14 to carbon-12 that is nearly identical with that of the atmosphere. Once the organism dies, however, it no longer ingests carbon compounds to replenish the carbon-14 lost through radioactive decay. The ratio of carbon-14 to carbon-12 therefore decreases. By measuring this ratio and comparing it with that of the atmosphere, we can estimate the age of an object. For example, if the ratio diminishes to half that of the atmosphere, we can conclude that the object is one half-life, or 5715 yr old.
This method cannot be used to date objects older than about 50,000 yr because after this length of time the radioactivity is too low to be measured accurately.
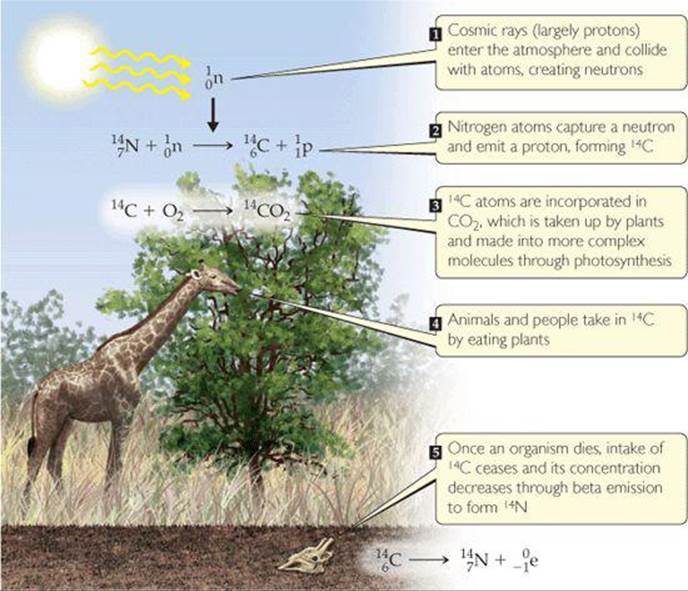
![]() FIGURE 21.7 Creation and distribution of carbon-14. The ratio of carbon-14 to carbon-12 in a dead animal or plant is related to the time since death occurred.
FIGURE 21.7 Creation and distribution of carbon-14. The ratio of carbon-14 to carbon-12 in a dead animal or plant is related to the time since death occurred.
In radiocarbon dating, a reasonable assumption is that the ratio of carbon-14 to carbon-12 in the atmosphere has been relatively constant for the past 50,000 yr. However, because variations in solar activity control the amount of carbon-14 produced in the atmosphere, that ratio can fluctuate. We can correct for this effect by using other kinds of data. Recently scientists have compared carbon-14 data with data from tree rings, corals, lake sediments, ice cores, and other natural sources to correct variations in the carbon-14 “clock” back to 26,000 yr.
Other isotopes can be similarly used to date other types of objects. For example, it takes 4.5 × 109 yr for half of a sample of uranium-238 to decay to lead-206. The age of rocks containing uranium can therefore be determined by measuring the ratio of lead-206 to uranium-238. If the lead-206 had somehow become incorporated into the rock by normal chemical processes instead of by radioactive decay, the rock would also contain large amounts of the more abundant isotope lead-208. In the absence of large amounts of this “geonormal” isotope of lead, it is assumed that all of the lead-206 was at one time uranium-238.
The oldest rocks found on Earth are approximately 3 × 109 yr old. This age indicates that Earth's crust has been solid for at least this length of time. Scientists estimate that it required 1 × 109 to 1.5 × 109 yr for Earth to cool and its surface to become solid, making the age of Earth 4.0 to 4.5 × 109 yr.
Calculations Based on Half-Life
So far, our discussion has been mainly qualitative. We now consider the topic of half-lives from a more quantitative point of view. This approach enables us to determine the half-life of a radioisotope or the age of an object.
As noted earlier, radioactive decay is a first-order kinetic process. Its rate, therefore, is proportional to the number of radioactive nuclei N in a sample:
![]()
The first-order rate constant, k, is called the decay constant.
The rate at which a sample decays is called its activity, and it is often expressed as number of disintegrations per unit time. The becquerel (Bq) is the SI unit for expressing activity. A becquerel is defined as one nuclear disintegration per second. An older, but still widely used, unit of activity is the curie (Ci), defined as 3.7 × 1010 disintegrations per second, which is the rate of decay of 1 g of radium. Thus, a 4.0-mCi sample of cobalt-60 undergoes

and so has an activity of 1.5 × 108 Bq.
As a radioactive sample decays, the amount of radiation emanating from the sample decays as well. For example, the half-life of cobalt-60 is 5.26 yr. The 4.0-mCi sample of cobalt-60 would, after 5.26 yr, have a radiation activity of 2.0 mCi, or 7.5 × 107 Bq.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
Why can't spontaneous radioactive decay be a zero-order or second-order kinetic process?
As we saw in Section 14.4, a first-order rate law can be transformed into the equation

In this equation t is the time interval of decay, k is the decay constant, N0 is the initial number of nuclei (at time zero), and Nt is the number remaining after the time interval. Both the mass of a particular radioisotope and its activity are proportional to the number of radioactive nuclei. Thus, either the ratio of the mass at any time t to the mass at time t = 0 or the ratio of the activities at time t and t = 0 can be substituted for Nt/N0 in Equation 21.19.
From Equation 21.19 we can obtain the relationship between the decay constant, k, and half-life, t1/2: ![]() (Section 14.4)
(Section 14.4)

where we have used the value ln (Nt/N0) = ln (0.5) = –0.693 for one half-life. Thus, if we know the value of either the decay constant or the half-life, we can calculate the value of the other.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
a. Would doubling the mass of a radioactive sample change the activity of the sample?
b. Would doubling the mass change the half-life for the radioactive decay?
SAMPLE EXERCISE 21.7 Calculating the Age of a Mineral
A rock contains 0.257 mg of lead-206 for every milligram of uranium-238. The half-life for the decay of uranium-238 to lead-206 is 4.5 × 109 yr. How old is the rock?
SOLUTION
Analyze We are told that a rock sample has a certain amount of lead-206 for every unit mass of uranium-238 and asked to estimate the age of the rock.
Plan Lead-206 is the product of the radioactive decay of uranium-238. We will assume that the only source of lead-206 in the rock is from the decay of uranium-238, with a known half-life. To apply first-order kinetics expressions (Equations 21.19 and 21.20) to calculate the time elapsed since the rock was formed, we first need to calculate how much initial uranium-238 there was for every 1 mg that remains today.
Solve Let's assume that the rock currently contains 1.000 mg of uranium-238 and therefore 0.257 mg of lead-206. The amount of uranium-238 in the rock when it was first formed therefore equals 1.000 mg plus the quantity that has decayed to lead-206. Because the mass of lead atoms is not the same as the mass of uranium atoms, we cannot just add 1.000 mg and 0.257 mg. We have to multiply the present mass of lead-206 (0.257 mg) by the ratio of the mass number of uranium to that of lead, into which it has decayed. Therefore, the original mass of ![]() was
was

Using Equation 21.20, we can calculate the decay constant for the process from its half-life:
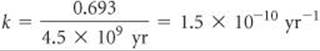
Rearranging Equation 21.19 to solve for time, t, and substituting known quantities gives
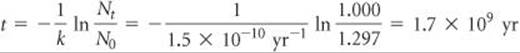
Comment To check this result, you could use the fact that the decay of uranium-237 to lead-207 has a half-life of 7 × 108 yr and measure the relative amounts of uranium-237 and lead-207 in the rock.
PRACTICE EXERCISE
A wooden object from an archeological site is subjected to radiocarbon dating. The activity due to 14C is measured to be 11.6 disintegrations per second. The activity of a carbon sample of equal mass from fresh wood is 15.2 disintegrations per second. The half-life of 14C is 5715 yr. What is the age of the archeological sample?
Answer: 2230 yr
We can also use measurements of radioactive activity to determine the half-life of a radioactive isotope, as the next sample exercise shows.
SAMPLE EXERCISE 21.8 Calculations Involving Radioactive Decay
If we start with 1.000 g of strontium-90, 0.953 g will remain after 2.00 yr. (a) What is the half-life of strontium-90? (b) How much strontium-90 will remain after 5.00 yr? (c) What is the initial activity of the sample in becquerels and curies?
SOLUTION
(a) Analyze We are asked to calculate a half-life, t1/2, based on data that tell us how much of a radioactive nucleus has decayed in a time interval t = 2.00 yr and the information N0 = 1.000 g, Nt = 0.953 g.
Plan We first calculate the rate constant for the decay, k, and then use that to compute t1/2.
Solve Equation 21.19 is solved for the decay constant, k, and then Equation 21.20 is used to calculate half-life, t1/2:
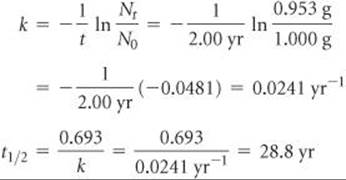
(b) Analyze We are asked to calculate the amount of a radionuclide remaining after a given period of time.
Plan We need to calculate Nt, the amount of strontium present at time t, using the initial quantity, N0, and the rate constant for decay, k, calculated in part (a).
Solve Again using Equation 21.19, with k = 0.0241 yr–1, we have
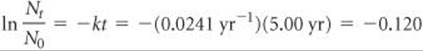
Nt/N0 is calculated from ln(Nt/N0) = –0.120 using the ex or INV LN function of a calculator:
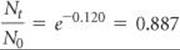
Because N0 = 1.000 g, we have
Nt = (0.887)N0 = (0.887)(1.000 g) = 0.887 g
(c) Analyze We are asked to calculate the activity of the sample in becquerels and curies.
Plan We must calculate the number of disintegrations per atom per second and then multiply by the number of atoms in the sample.
Solve The number of disintegrations per atom per second is given by the rate constant, k:
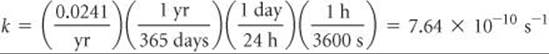
To obtain the total number of disintegrations per second, we calculate the number of atoms in the sample. We multiply this quantity by k, where we express k as the number of disintegrations per atom per second, to obtain the number of disintegrations per second:

Because 1 Bq is one disintegration per second, the activity is 5.1 × 1012 Bq. The activity in curies is given by
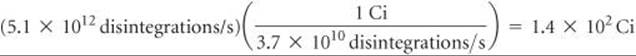
We have used only two significant figures in products of these calculations because we do not know the atomic weight of 90Sr to more than two significant figures without looking it up in a special source.
PRACTICE EXERCISE
A sample to be used for medical imaging is labeled with 18F, which has a half-life of 110 min. What percentage of the original activity in the sample remains after 300 min?
Answer: 15.1%