CHEMISTRY THE CENTRAL SCIENCE
APPENDIX A
MATHEMATICAL OPERATIONS
A.1 EXPONENTIAL NOTATION
The numbers used in chemistry are often either extremely large or extremely small. Such numbers are conveniently expressed in the form
N × 10n
where N is a number between 1 and 10, and n is the exponent. Some examples of this exponential notation, which is also called scientific notation, follow.
1,200,000 is 1.2 × 106 (read “one point two times ten to the sixth power”)
0.000604 is 6.04 × 10–4 (read “six point zero four times ten to the negative fourth power”)
A positive exponent, as in the first example, tells us how many times a number must be multiplied by 10 to give the long form of the number:
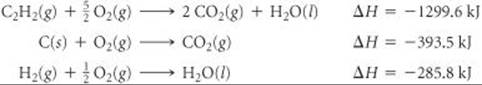
It is also convenient to think of the positive exponent as the number of places the decimal point must be moved to the left to obtain a number greater than 1 and less than 10. For example, if we begin with 3450 and move the decimal point three places to the left, we end up with 3.45 × 103
In a related fashion, a negative exponent tells us how many times we must divide a number by 10 to give the long form of the number.
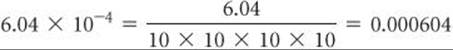
It is convenient to think of the negative exponent as the number of places the decimal point must be moved to the right to obtain a number greater than 1 but less than 10. For example, if we begin with 0.0048 and move the decimal point three places to the right, we end up with 4.8 × 10–3
In the system of exponential notation, with each shift of the decimal point one place to the right, the exponent decreases by 1:
4.8 × 10–3 = 48 × 10–4
Similarly, with each shift of the decimal point one place to the left, the exponent increases by 1:
4.8 × 10–3 = 0.48 × 10–2
Many scientific calculators have a key labeled EXP or EE, which is used to enter numbers in exponential notation. To enter the number 5.8 × 103 on such a calculator, the key sequence is
On some calculators the display will show 5.8, then a space, followed by 03, the exponent. On other calculators, a small 10 is shown with an exponent 3.
To enter a negative exponent, use the key labeled +/– For example, to enter the number 8.6 × 10–5, the key sequence is
When entering a number in exponential notation, do not key in the 10 if you use the EXP or EE button.
In working with exponents, it is important to recall that 100 = 1. The following rules are useful for carrying exponents through calculations.
1. Addition and Subtraction In order to add or subtract numbers expressed in exponential notation, the powers of 10 must be the same.
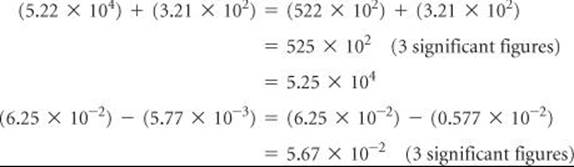
When you use a calculator to add or subtract, you need not be concerned with having numbers with the same exponents because the calculator automatically takes care of this matter.
2. Multiplication and Division When numbers expressed in exponential notation are multiplied, the exponents are added; when numbers expressed in exponential notation are divided, the exponent of the denominator is subtracted from the exponent of the numerator.
3. Powers and Roots When numbers expressed in exponential notation are raised to a power, the exponents are multiplied by the power. When the roots of numbers expressed in exponential notation are taken, the exponents are divided by the root.
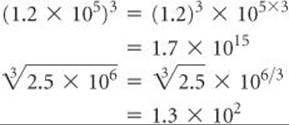
Scientific calculators usually have keys labeled x2 and 
for squaring and taking the square root of a number, respectively. To take higher powers or roots, many calculators have yx and 
(or INV yx) keys. For example, to perform the operation 
on such a calculator, you would key in 7.5 × 10–4, press the 
key (or the INV and then the yx keys), enter the root, 3, and finally press = . The result is 9.1 × 10–2
SAMPLE EXERCISE 1 Using Exponential Notation
Perform each of the following operations, using your calculator where possible:
(a) Write the number 0.0054 in standard exponential notation.
(b) (5.0 × 10–2) + (4.7 × 10–3)
(c) (5.98 × 1012)(2.77 × 10–5)
SOLUTION
(a) Because we move the decimal point three places to the right to convert 0.0054 to 5.4, the exponent is –3:
5.4 × 10–3
Scientific calculators are generally able to convert numbers to exponential notation using one or two keystrokes; frequently “SCI” for “scientific notation” will convert a number into exponential notation. Consult your instruction manual to see how this operation is accomplished on your calculator.
(b) To add these numbers longhand, we must convert them to the same exponent.
(5.0 × 10–2) + (0.47 × 10–2) = (5.0 + 0.47) × 10–2 = 5.5 × 10–2
(Note that the result has only two significant figures.) To perform this operation on a calculator, we enter the first number, strike the + key, then enter the second number and strike the = key.
(c) Performing this operation longhand, we have
(5.98 × 2.77) × 1012–5 = 16.6 × 107 = 1.66 × 108
On a scientific calculator, we enter 5.98 × 1012, press the × key, enter 2.77 × 10–5, and press the = key.
(d) To perform this operation on a calculator, we enter the number, press the key (or the INV and keys), enter 4, and press the = key. The result is 1.15 × 010–5.
PRACTICE EXERCISE
Perform the following operations:
(a) Write 67,000 in exponential notation, showing two significant figures.
(b) (3.378 × 10–3) – (4.97 × 10–5)
(c) (1.84 × 1015)(7.45 × 10–2)
(d) (6.67 × 10–8)3
Answers: (a) 6.7 × 104, (b) 3.328 × 10–3, (c) 2.47 × 1016, (d) 2.97 × 10–22
A.2 LOGARITHMS
Common Logarithms
The common, or base-10, logarithm (abbreviated log) of any number is the power to which 10 must be raised to equal the number. For example, the common logarithm of 1000 (written log 1000) is 3 because raising 10 to the third power gives 1000.
103 = 1000, therefore, log 1000 = 3
Further examples are
In these examples the common logarithm can be obtained by inspection. However, it is not possible to obtain the logarithm of a number such as 31.25 by inspection. The logarithm of 31.25 is the number x that satisfies the following relationship:
10x = 31.25
Most electronic calculators have a key labeled LOG that can be used to obtain logarithms. For example, on many calculators we obtain the value of log 31.25 by entering 31.25 and pressing the LOG key. We obtain the following result:
log 31.25 = 1.4949
Notice that 31.25 is greater than 10 (101) and less than 100 (102). The value for log 31.25 is accordingly between log 10 and log 100, that is, between 1 and 2.
Significant Figures and Common Logarithms
For the common logarithm of a measured quantity, the number of digits after the decimal point equals the number of significant figures in the original number. For example, if 23.5 is a measured quantity (three significant figures), then log 23.5 = 1.371 (three significant figures after the decimal point).
Antilogarithms
The process of determining the number that corresponds to a certain logarithm is known as obtaining an antilogarithm. It is the reverse of taking a logarithm. For example, we saw previously that log 23.5 = 1.371. This means that the antilogarithm of 1.371 equals 23.5.
The process of taking the antilog of a number is the same as raising 10 to a power equal to that number.
antilog 1.371 = 101.371 = 23.5
Many calculators have a key labeled 10x that allows you to obtain antilogs directly. On others, it will be necessary to press a key labeled INV (for inverse), followed by the LOG key.
Natural Logarithms
Logarithms based on the number e are called natural, or base e, logarithms (abbreviated ln). The natural log of a number is the power to which e (which has the value 2.71828...) must be raised to equal the number. For example, the natural log of 10 equals 2.303.
Your calculator probably has a key labeled LN that allows you to obtain natural logarithms. For example, to obtain the natural log of 46.8, you enter 46.8 and press the LN key.
ln 46.8 = 3.846
The natural antilog of a number is e raised to a power equal to that number. If your calculator can calculate natural logs, it will also be able to calculate natural antilogs. On some calculators there is a key labeled ex that allows you to calculate natural antilogs directly; on others, it will be necessary to first press the INV key followed by the LN key. For example, the natural antilog of 1.679 is given by
Natural antilog 1.679 = e1.679 = 5.36
The relation between common and natural logarithms is as follows:
ln a = 2.303 log a
Notice that the factor relating the two, 2.303, is the natural log of 10, which we calculated earlier.
Mathematical Operations Using Logarithms
Because logarithms are exponents, mathematical operations involving logarithms follow the rules for the use of exponents. For example, the product of za and zb (where z is any number) is given by
Similarly, the logarithm (either common or natural) of a product equals the sum of the logs of the individual numbers.
log ab = log a + log b ln ab = ln a + ln b
For the log of a quotient,
log(a/b) = log a – log b ln(a/b) = ln a – ln b
Using the properties of exponents, we can also derive the rules for the logarithm of a number raised to a certain power.
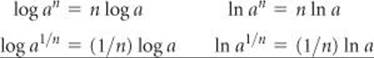
pH Problems
One of the most frequent uses for common logarithms in general chemistry is in working pH problems. The pH is defined as –log[H+], where [H+] is the hydrogen ion concentration of a solution. 
(Section 16.4) The following sample exercise illustrates this application.
SAMPLE EXERCISE 2 Using Logarithms
(a) What is the pH of a solution whose hydrogen ion concentration is 0.015 M?
(b) If the pH of a solution is 3.80, what is its hydrogen ion concentration?
SOLUTION
1. We are given the value of [H+]. We use the LOG key of our calculator to calculate the value of log[H+]. The pH is obtained by changing the sign of the value obtained. (Be sure to change the sign after taking the logarithm.)
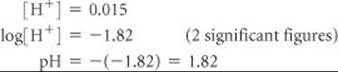
2. To obtain the hydrogen ion concentration when given the pH, we must take the antilog of –pH.
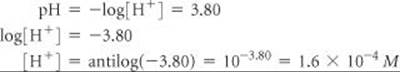
PRACTICE EXERCISE
Perform the following operations: (a) log(2.5 × 10–5),(b) ln 32.7, (c) antilog –3.47 (d) e–1.89.
Answers: (a) –4.60, (b) 3.487, (c) 3.4 × 10–4, (d) 1.5 × 10–1
A.3 QUADRATIC EQUATIONS
An algebraic equation of the form ax2 + bx + c = 0 is called a quadratic equation. The two solutions to such an equation are given by the quadratic formula:
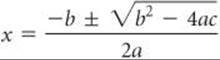
Many calculators today can calculate the solutions to a quadratic equation with one or two keystrokes. Most of the time, x corresponds to the concentration of a chemical species in solution. Only one of the solutions will be a positive number, and that is the one you should use; a “negative concentration” has no physical meaning.
SAMPLE EXERCISE 3 Using the Quadratic Formula
Find the values of x that satisfy the equation 2x2 + 4x = 1.
SOLUTION
To solve the given equation for x, we must first put it in the form
ax2 + bx + c = 0
and then use the quadratic formula. If
2x2 + 4x = 1
then
2x2 + 4x – 1 = 0
Using the quadratic formula, where a = 2, b = 4, and c = – 1, we have
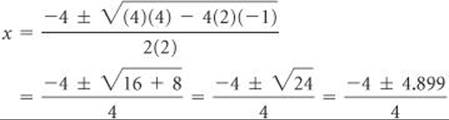
The two solutions are
If this was a problem in which x represented a concentration, we would say x = 0.225 (in the appropriate units), since a negative number for concentration has no physical meaning.
A.4 GRAPHS
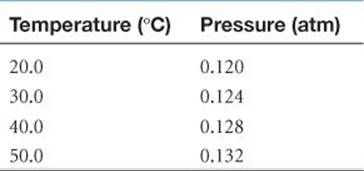
Often the clearest way to represent the interrelationship between two variables is to graph them. Usually, the variable that is being experimentally varied, called the independent variable, is shown along the horizontal axis (x-axis). The variable that responds to the change in the independent variable, called the dependent variable, is then shown along the vertical axis (y-axis). For example, consider an experiment in which we vary the temperature of an enclosed gas and measure its pressure. The independent variable is temperature, and the dependent variable is pressure. The data shown in 
TABLE A.1 can be obtained by means of this experiment. These data are shown graphically in 
FIGURE A.1. The relationship between temperature and pressure is linear. The equation for any straight-line graph has the form
y = mx + b
TABLE A.1 • Interrelation between Pressure and Temperature
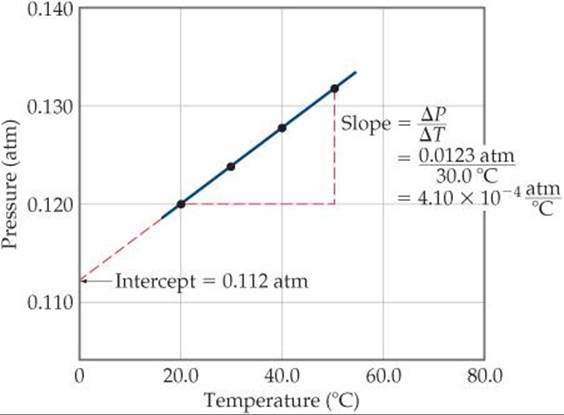
FIGURE A.1 A graph of pressure versus temperature yields a straight line for the data.
where m is the slope of the line and b is the intercept with the y-axis. In the case of Figure A.1, we could say that the relationship between temperature and pressure takes the form
P = mT + b
where P is pressure in atm and T is temperature in °C. As shown in Figure A.1, the slope is 4.10 × 10–4 atm/°C, and the intercept—the point where the line crosses the y-axis—is 0.112 atm. Therefore, the equation for the line is
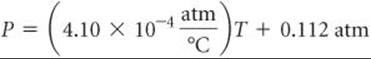
A.5 STANDARD DEVIATION
The standard deviation from the mean, s, is a common method for describing precision in experimentally determined data. We define the standard deviation as
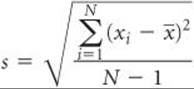
where N is the number of measurements, 
is the average (also called the mean) of the measurements, and xi represents the individual measurements. Electronic calculators with built-in statistical functions can calculate s directly by inputting the individual measurements.
A smaller value of s indicates a higher precision, meaning that the data are more closely clustered around the average. The standard deviation has statistical significance. If a large number of measurements is made, 68% of the measured values is expected to be within one standard deviation of the average, assuming only random errors are associated with the measurements.
SAMPLE EXERCISE 4 Calculating an Average and Standard Deviation
The percent carbon in a sugar is measured four times: 42.01%, 42.28%, 41.79%, and 42.25%. Calculate (a) the average and (b) the standard deviation for these measurements.
SOLUTION
(a) The average is found by adding the quantities and dividing by the number of measurements:
(b) The standard deviation is found using the preceding equation:
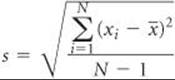
Let's tabulate the data so the calculation of a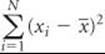 
can be seen clearly.
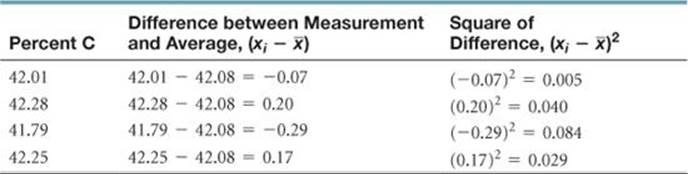
The sum of the quantities in the last column is
Thus, the standard deviation is
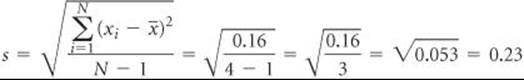
Based on these measurements, it would be appropriate to represent the measured percent carbon as 42.08 ± 0.23.