CHEMISTRY THE CENTRAL SCIENCE

1 INTRODUCTION: MATTER AND MEASUREMENT

EXERCISES

VISUALIZING CONCEPTS

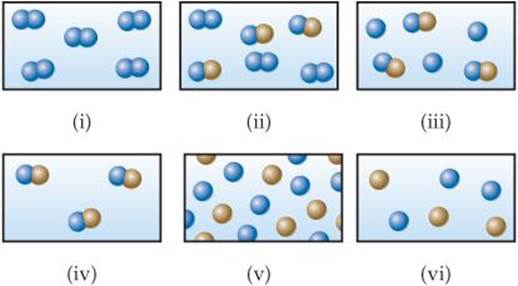
1.1 Which of the following figures represents (a) a pure element, (b) a mixture of two elements, (c) a pure compound, (d) a mixture of an element and a compound? (More than one picture might fit each description.) [Section 1.2]

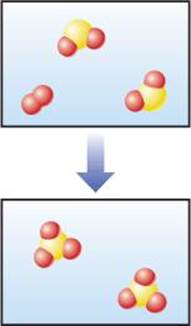
1.2 Does the following diagram represent a chemical or physical change? How do you know? [Section 1.3]

1.3 Describe the separation method(s) involved in brewing a cup of coffee. [Section 1.3]

1.4 Identify each of the following as measurements of length, area, volume, mass, density, time, or temperature: (a) 25 ps, (b) 374.2 mg, (c) 77 K, (d) 100,000 km², (e) 1.06 μm, (f) 16 nm²(g) −78 °C, (h) 2.56 g/cm³, (i) 28 cm³. [Section 1.4]

1.5 (a) Three spheres of equal size are composed of aluminum (density = 2.70 g/cm³), silver (density = 10.49 g/cm³), and nickel (density = 8.90 g/cm³). List the spheres from lightest to heaviest. (b) Three cubes of equal mass are composed of gold (density = 19.32 g/cm³), platinum (density = 21.45 g/cm³), and lead (density = 11.35 g/cm³). List the cubes from smallest to largest. [Section 1.4]

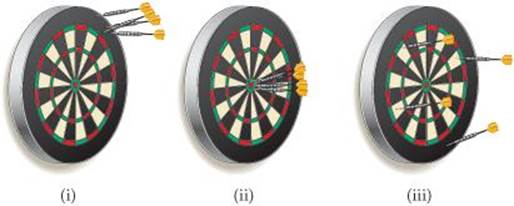
1.6 The following dartboards illustrate the types of errors often seen when one measurement is repeated several times. The bull's-eye represents the “true value,” and the darts represent the experimental measurements. Which board best represents each of the following scenarios: (a)measurements both accurate and precise, (b) measurements precise but inaccurate, (c) measurements imprecise but yielding an accurate average? [Section 1.5]

1.7 (a) What is the length of the pencil in the following figure if the ruler reads in centimeters? How many significant figures are there in this measurement? (b) An automobile speedometer with circular scales reading both miles per hour and kilometers per hour is shown. What speed is indicated, in both units? How many significant figures are in the measurements? [Section 1.5]

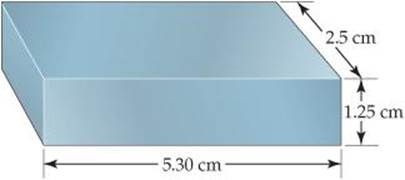
1.8 (a) How many significant figures should be reported for the volume of the metal bar shown here? (b) If the mass of the bar is 104.72 g, how many significant figures should be reported when its density is determined using the calculated volume? [Section 1.5]

1.9 When you convert units, how do you decide which part of the conversion factor is in the numerator and which is in the denominator? [Section 1.6]

1.10 Show the steps to convert the speed of sound, 344 meters per second, into miles per hour. [Section 1.6]

CLASSIFICATION AND PROPERTIES OF MATTER (sections 1.2 and 1.3)

1.11 Classify each of the following as a pure substance or a mixture. If a mixture, indicate whether it is homogeneous or heterogeneous: (a) rice pudding, (b) seawater, (c) magnesium, (d) crushed ice.

1.12 Classify each of the following as a pure substance or a mixture. If a mixture, indicate whether it is homogeneous or heterogeneous: (a) air, (b) tomato juice, (c) iodine crystals, (d) sand.

______

1.13 Give the chemical symbol or name for the following elements, as appropriate: (a) sulfur, (b) gold, (c) potassium, (d) chlorine, (e) copper, (f) U, (g) Ni, (h) Na, (i) Al, (j) Si.

1.14 Give the chemical symbol or name for each of the following elements, as appropriate: (a) carbon, (b) nitrogen, (c) titanium, (d) zinc, (e) iron, (f) P, (g) Ca, (h) He, (i) Pb, (j) Ag.

______

1.15 A solid white substance A is heated strongly in the absence of air. It decomposes to form a new white substance B and a gas C. The gas has exactly the same properties as the product obtained when carbon is burned in an excess of oxygen. Based on these observations, can we determine whether solids A and B and gas C are elements or compounds? Explain your conclusions for each substance.

1.16 You are hiking in the mountains and find a shiny gold nugget. It might be the element gold, or it might be “fool's gold,” which is a nickname for iron pyrite, FeS₂. What kinds of experiments could be done to determine if the shiny nugget is really gold?

______

1.17 In the process of attempting to characterize a substance, a chemist makes the following observations: The substance is a silvery white, lustrous metal. It melts at 649 °C and boils at 1105 °C. Its density at 20 °C is 1.738g/cm³. The substance burns in air, producing an intense white light. It reacts with chlorine to give a brittle white solid. The substance can be pounded into thin sheets or drawn into wires. It is a good conductor of electricity. Which of these characteristics are physical properties, and which are chemical properties?

1.18 Read the following description of the element zinc and indicate which are physical properties and which are chemical properties. Zinc is a silver-gray–colored metal that melts at 420 °C. When zinc granules are added to dilute sulfuric acid, hydrogen is given off and the metal dissolves. Zinc has a hardness on the Mohs scale of 2.5 and a density of 7.13 g/cm³ at 25 °C. It reacts slowly with oxygen gas at elevated temperatures to form zinc oxide, ZnO.

______

1.19 Label each of the following as either a physical process or a chemical process: (a) rusting of a metal can, (b) boiling a cup of water, (c) pulverizing an aspirin, (d) digesting a candy bar, (e) exploding of nitroglycerin.

1.20 A match is lit and held under a cold piece of metal. The following observations are made: (a) The match burns. (b) The metal gets warmer. (c) Water condenses on the metal. (d) Soot (carbon) is deposited on the metal. Which of these occurrences are due to physical changes, and which are due to chemical changes?

______

1.21 Suggest a method of separating each of the following mixtures into two components: (a) sugar and sand, (b) oil and vinegar.

1.22 Three beakers contain clear, colorless liquids. One beaker contains pure water, another contains salt water, and another contains sugar water. How can you tell which beaker is which? (No tasting allowed!)

UNITS AND MEASUREMENT (section 1.4)

1.23 What exponential notation do the following abbreviations represent: (a) d, (b) c, (c) f, (d) μ, (e) M, (f) k, (g) n, (h) m, (i) p?

1.24 Use appropriate metric prefixes to write the following measurements without use of exponents: (a) 2.3 × 10^–10 L, (b) 4.7 × 10^–6 g, (c) 1.85 × 10^–12 m, (d) 16.7 × 10⁶ s; (e) 15.7 × 10³ g, (f) 1.34 × 10^–3 m, (g) 1.84 × 10² cm.

______

1.25 Make the following conversions: (a) 72 °F to °C, (b) 216.7 °C to °F, (c) 233 °C to K, (d) 315 K to °F, (e) 2500 °F to K, (f) 0 K to °F.

1.26 (a) The temperature on a warm summer day is 87 °F. What is the temperature in °C? (b) Many scientific data are reported at 25 °C. What is this temperature in kelvins and in degrees Fahrenheit? (c) Suppose that a recipe calls for an oven temperature of 400 °F. Convert this temperature to degrees Celsius and to kelvins. (d) Liquid nitrogen boils at 77 K. Convert this temperature to degrees Fahrenheit and to degrees Celsius.

______

1.27 (a) A sample of tetrachloroethylene, a liquid used in dry cleaning that is being phased out because of its potential to cause cancer, has a mass of 40.55 g and a volume of 25.0 mL at 25 °C. What is its density at this temperature? Will tetrachloroethylene float on water? (Materials that are less dense than water will float.) (b) Carbon dioxide (CO₂) is a gas at room temperature and pressure. However, carbon dioxide can be put under pressure to become a “supercritical fluid” that is a much safer drycleaning agent than tetrachloroethylene. At a certain pressure, the density of supercritical CO₂ is 0.469 g/cm³. What is the mass of a 25.0-mL sample of supercritical CO₂ at this pressure?

1.28 (a) A cube of osmium metal 1.500 cm on a side has a mass of 76.31 g at 25 °C. What is its density in g/cm³ at this temperature? (b) The density of titanium metal is 4.51 g/cm³ at 25 °C. What mass of titanium displaces 125.0 mL of water at 25 °C? (c) The density of benzene at 15 °C is 0.8787. Calculate the mass of 0.1500 L of benzene at this temperature.

______

1.29 (a) To identify a liquid substance, a student determined its density. Using a graduated cylinder, she measured out a 45-mL sample of the substance. She then measured the mass of the sample, finding that it weighed 38.5 g. She knew that the substance had to be either isopropyl alcohol (density 0.785 g/mL) or toluene (density 0.866 g/mL). What are the calculated density and the probable identity of the substance? (b) An experiment requires 45.0 g of ethylene glycol, a liquid whose density is 1.114 g/mL. Rather than weigh the sample on a balance, a chemist chooses to dispense the liquid using a graduated cylinder. What volume of the liquid should he use? (c) A cubic piece of metal measures 5.00 cm on each edge. If the metal is nickel, whose density is 8.90 g/cm³, what is the mass of the cube?

1.30 (a) After the label fell off a bottle containing a clear liquid believed to be benzene, a chemist measured the density of the liquid to verify its identity. A 25.0-mL portion of the liquid had a mass of 21.95 g. A chemistry handbook lists the density of benzene at 15 °C as 0.8787 g/mL. Is the calculated density in agreement with the tabulated value? (b) An experiment requires 15.0 g of cyclohexane, whose density at 25 °C is 0.7781 g/mL. What volume of cyclohexane should be used? (c) A spherical ball of lead has a diameter of 5.0 cm. What is the mass of the sphere if lead has a density of 11.34 g/cm³? (The volume of a sphere is (4/3)πr³ where r is the radius.)

______

1.31 In the year 2007, an estimated amount of 31 billion tons of carbon dioxide (CO₂) was emitted worldwide due to fossil fuel combustion and cement production. Express this mass of CO₂ in grams without exponential notation, using an appropriate metric prefix.

1.32 Silicon for computer chips is grown in large cylinders called “boules” that are 300 mm in diameter and 2 m in height. The density of silicon is 2.33 g/cm³. Silicon wafers for making integrated circuits are sliced from a 2.0 m boule and are typically 0.75 mm thick and 300 mm in diameter. (a) How many wafers can be cut from a single boule? (b) What is the mass of a silicon wafer? (The volume of a cylinder is given by πr²h, where r is the radius and h is its height.)

UNCERTAINTY IN MEASUREMENT (section 1.5)

1.33 Indicate which of the following are exact numbers: (a) the mass of a piece of paper, (b) the volume of a cup of coffee, (c) the number of inches in a mile, (d) the number of ounces in a pound, (e) the number of microseconds in a week, (f) the number of pages in this book.

1.34 Indicate which of the following are exact numbers: (a) the mass of a 32-oz can of coffee, (b) the number of students in your chemistry class, (c) the temperature of the surface of the sun, (d) the mass of a postage stamp, (e) the number of milliliters in a cubic meter of water, (f) the average height of students in your school.

______

1.35 What is the number of significant figures in each of the following measured quantities? (a) 601 kg, (b) 0.054 s, (c) 6.3050 cm, (d) 0.0105 L, (e) 7.0500 × 10^–3 m³, (f) 400 g.

1.36 Indicate the number of significant figures in each of the following measured quantities: (a) 3.774 km, (b) 205 m², (c) 1.700 cm, (d) 350.00 K, (e) 307.080 g, (f) 1.3 × 10³ m/s.

______

1.37 Round each of the following numbers to four significant figures, and express the result in standard exponential notation: (a) 102.53070, (b) 656,980, (c) 0.008543210, (d) 0.000257870, (e) –0.0357202.

1.38 (a) The diameter of Earth at the equator is 7926.381 mi. Round this number to three significant figures, and express it in standard exponential notation. (b) The circumference of Earth through the poles is 40,008 km. Round this number to four significant figures, and express it in standard exponential notation.

______

1.39 Carry out the following operations, and express the answers with the appropriate number of significant figures.

(a) 14.3505 + 2.65

(b) 952.7 – 140.7389

(c) (3.29 × 10⁴)(0.2501)

(d) 0.0588/0.677

1.40 Carry out the following operations, and express the answer with the appropriate number of significant figures.

(a) 320.5 – (6104.5/2.3)

(b) [(285.3 × 10⁵) – (1.200 × 10³)] × 2.8954

(c) (0.0045 × 20,000.0) + (2813 × 12)

(d) 863 × [1255 – (3.45 × 108)]

______

1.41 You weigh an object on a balance and read the mass in grams according to the picture. How many significant figures are in this measurement?

1.42 You have a graduated cylinder that contains a liquid (see photograph). Write the volume of the liquid, in milliliters, using the proper number of significant figures.

______

DIMENSIONAL ANALYSIS (section 1.6)

1.43 Using your knowledge of metric units, English units, and the information on the back inside cover, write down the conversion factors needed to convert (a) mm to nm, (b) mg to kg, (c) km to ft, (d) in.³ to cm³.

1.44 Using your knowledge of metric units, English units, and the information on the back inside cover, write down the conversion factors needed to convert (a) μm to mm, (b) ms to ns, (c) mi to km, (d) ft³ to L.

______

1.45 (a) A bumblebee flies with a ground speed of 15.2 m/s. Calculate its speed in km/h. (b) The lung capacity of the blue whale is 5.0 × 10³L. Convert this volume into gallons. (c) The Statue of Liberty is 151 ft tall. Calculate its height in meters. (d) Bamboo can grow up to 60.0 cm/day. Convert this growth rate into inches per hour.

1.46 (a) The speed of light in a vacuum is 2.998 × 10⁸m/s. Calculate its speed in miles per hour. (b) The Sears Tower in Chicago is 1454 ft tall. Calculate its height in meters. (c) The Vehicle Assembly Building at the Kennedy Space Center in Florida has a volume of 3,666,500 m³. Convert this volume to liters and express the result in standard exponential notation. (d) An individual suffering from a high cholesterol level in her blood has 242 mg of cholesterol per 100 mL of blood. If the total blood volume of the individual is 5.2 L, how many grams of total blood cholesterol does the individual's body contain?

______

1.47 Perform the following conversions: (a) 5.00 days to s, (b) 0.0550 mi to m, (c) $1.89/gal to dollars per liter, (d) 0.510 in./ms to km/hr, (e) 22.50 gal/min to L/s, (f) 0.02500 ft³ to cm³.

1.48 Carry out the following conversions: (a) 0.105 in. to mm, (b) 0.650 qt to mL, (c) 8.75 μm/s to km/hr, (d) 1.955 m³ to yd³, (e) $3.99/lb to dollars per kg, (f) 8.75 lb/ft³ to g/mL.

______

1.49 (a) How many liters of wine can be held in a wine barrel whose capacity is 31 gal? (b) The recommended adult dose of Elixophyllin ®, a drug used to treat asthma, is 6 mg/kg of body mass. Calculate the dose in milligrams for a 185-lb person. (c) If an automobile is able to travel 400 km on 47.3 L of gasoline, what is the gas mileage in miles per gallon? (d) A pound of coffee beans yields 50 cups of coffee (4 cups = 1 qt). How many milliliters of coffee can be obtained from 1 g of coffee beans?

1.50 (a) If an electric car is capable of going 225 km on a single charge, how many charges will it need to travel from Seattle, Washington, to San Diego, California, a distance of 1257 mi, assuming that the trip begins with a full charge? (b) If a migrating loon flies at an average speed of 14m/s, what is its average speed in mi/hr? (c) What is the engine piston displacement in liters of an engine whose displacement is listed as 450 in.³? (d) In March 1989 the Exxon Valdez ran aground and spilled 240,000 barrels of crude petroleum off the coast of Alaska. One barrel of petroleum is equal to 42 gal. How many liters of petroleum were spilled?

______

1.51 The density of air at ordinary atmospheric pressure and 25 °C is 1.19g/L. What is the mass, in kilograms, of the air in a room that measures 14.5ft × 16.5ft × 8.0 ft?

1.52 The concentration of carbon monoxide in an urban apartment is 48 μg/m³. What mass of carbon monoxide in grams is present in a room measuring 11.0 ft × 11.5ft × 20.5ft?

______

1.53 By using estimation techniques, arrange these items in order from shortest to longest: a 57-cm length of string, a 14-in.-long shoe, and a 1.1-m length of pipe.

1.54 By using estimation techniques, determine which of the following is the heaviest and which is the lightest: a 5-lb bag of potatoes, a 5-kg bag of sugar, or 1 gal of water (density = 1.0 g/mL).

______

1.55 Gold can be hammered into extremely thin sheets called gold leaf. An architect wants to cover a 100 ft × 82ft ceiling with gold leaf that is five-millionths of an inch thick. The density of gold is 19.32 g/cm³, and gold costs $953 per troy ounce (1 troy ounce = 31.1034768 g). How much will it cost the architect to buy the necessary gold?

1.56 A copper refinery produces a copper ingot weighing 150 lb. If the copper is drawn into wire whose diameter is 7.50 mm, how many feet of copper can be obtained from the ingot? The density of copper is 8.94 g/cm³. (Assume that the wire is a cylinder whose volume V = πr²h, where r is its radius and h is its height or length.)

______

ADDITIONAL EXERCISES

1.57 (a) Classify each of the following as a pure substance, a solution, or a heterogeneous mixture: a gold coin, a cup of coffee, a wood plank. (b) What ambiguities are there in answering part (a) from the descriptions given?

1.58 (a) What is the difference between a hypothesis and a theory? (b) Explain the difference between a theory and a scientific law. Which addresses how matter behaves, and which addresses why it behaves that way?

1.59 A sample of ascorbic acid (vitamin C) is synthesized in the laboratory. It contains 1.50 g of carbon and 2.00 g of oxygen. Another sample of ascorbic acid isolated from citrus fruits contains 6.35 g of carbon. How many grams of oxygen does it contain? Which law are you assuming in answering this question?

1.60 Two students determine the percentage of lead in a sample as a laboratory exercise. The true percentage is 22.52%. The students' results for three determinations are as follows:

1. 22.52, 22.48, 22.54

2. 22.64, 22.58, 22.62

(a) Calculate the average percentage for each set of data, and state which set is the more accurate based on the average. (b) Precision can be judged by examining the average of the deviations from the average value for that data set. (Calculate the average value for each data set; then calculate the average value of the absolute deviations of each measurement from the average.) Which set is more precise?

1.61 Is the use of significant figures in each of the following statements appropriate? Why or why not? (a) Apple sold 22,727,000 iPods during the last three months of 2008. (b) New York City receives 49.7 inches of rain, on average, per year. (c) In the United States, 0.621% of the population has the surname Brown. (d) You calculate your grade point average to be 3.87562.

1.62 What type of quantity (for example, length, volume, density) do the following units indicate: (a) mL, (b) cm², (c) mm³, (d) mg/L, (e) ps, (f) nm, (g) K?

1.63 Give the derived SI units for each of the following quantities in base SI units: (a) acceleration = distance/time², (b) force = mass × acceleration, (c) work = force × distance, (d) pressure = force/area, (e) power = work/time, (f) velocity = distance/time, (g) energy = mass × (velocity)².

1.64 The distance from Earth to the Moon is approximately 240,000 mi. (a) What is this distance in meters? (b) The peregrine falcon has been measured as traveling up to 350 km/hr in a dive. If this falcon could fly to the Moon at this speed, how many seconds would it take? (c) The speed of light is 3.00 × 10⁸m/s. How long does it take for light to travel from Earth to the Moon and back again? (d) Earth travels around the Sun at an average speed of 29.783 km/s. Convert this speed to miles per hour.

1.65 The US quarter has a mass of 5.67 g and is approximately 1.55 mm thick. (a) How many quarters would have to be stacked to reach 575 ft, the height of the Washington Monument? (b) How much would this stack weigh? (c) How much money would this stack contain? (d) The US National Debt Clock showed the outstanding public debt to be $11,687,233,914,811.11 on August 19, 2009. How many stacks like the one described would be necessary to pay off this debt?

1.66 In the United States, water used for irrigation is measured in acre-feet. An acre-foot of water covers an acre to a depth of exactly 1 ft. An acre is 4840 yd². An acre-foot is enough water to supply two typical households for 1.00 yr. (a) If desalinated water costs $1950 per acre-foot, how much does desalinated water cost per liter? (b) How much would it cost one household per day if it were the only source of water?

1.67 Suppose you decide to define your own temperature scale using the freezing point (13 °C) and boiling point (360 °C) of oleic acid, the main component of olive oil. If you set the freezing point of oleic acid as 0 °O and the boiling point as 100 °O, what is the freezing point of water on this new scale?

1.68 The liquid substances mercury (density = 13.6 g/mL), water (1.00 g/mL), and cyclohexane (0.778 g/mL) do not form a solution when mixed but separate in distinct layers. Sketch how the liquids would position themselves in a test tube.

1.69 Two spheres of equal volume are placed on the scales as shown. Which one is more dense?

1.70 Water has a density of 0.997 g/cm³ at 25 °C; ice has a density of 0.917 g/cm³ at –10 °C. (a) If a soft-drink bottle whose volume is 1.50 L is completely filled with water and then frozen to –10 °C, what volume does the ice occupy? (b) Can the ice be contained within the bottle?

1.71 A 32.65-g sample of a solid is placed in a flask. Toluene, in which the solid is insoluble, is added to the flask so that the total volume of solid and liquid together is 50.00 mL. The solid and toluene together weigh 58.58 g. The density of toluene at the temperature of the experiment is 0.864 g/mL. What is the density of the solid?

1.72 A thief plans to steal a gold sphere with a radius of 28.9 cm from a museum. If the gold has a density of 19.3 g/cm³, what is the mass of the sphere in pounds? [The volume of a sphere is V = (4/3)πr³.] Is the thief likely to be able to walk off with the gold sphere unassisted?

1.73 Automobile batteries contain sulfuric acid, which is commonly referred to as “battery acid.” Calculate the number of grams of sulfuric acid in 1.00 gallon of battery acid if the solution has a density of 1.28 g/mL and is 38.1% sulfuric acid by mass.

1.74 A 40-lb container of peat moss measures 14 × 20 × 30 in. A 40-lb container of topsoil has a volume of 1.9 gal. (a) Calculate the average densities of peat moss and topsoil in units of g/cm³. Would it be correct to say that peat moss is “lighter” than topsoil? Explain. (b) How many bags of peat moss are needed to cover an area measuring 15.0 ft × 20.0 ft to a depth of 3.0 in.?

1.75 A package of aluminum foil contains 50 ft² of foil, which weighs approximately 8.0 oz. Aluminum has a density of 2.70 g/cm³. What is the approximate thickness of the foil in millimeters?

1.76 The total power used by humans worldwide is approximately 15 TW (terawatts). Sunlight striking Earth provides 1.336 kW per square meter (assuming no clouds). The surface area of Earth is approximately 197,000,000 square miles. How much of Earth's surface would we need to cover with solar energy collectors to power the planet for use by all humans? Assume that the solar energy collectors can only convert 10% of the available sunlight into useful power.

1.77 A 15.0-cm long cylindrical glass tube, sealed at one end, is filled with ethanol. The mass of ethanol needed to fill the tube is found to be 11.86 g. The density of ethanol is 0.789 g/mL. Calculate the inner diameter of the tube in centimeters.

1.78 Gold is alloyed (mixed) with other metals to increase its hardness in making jewelry. (a) Consider a piece of gold jewelry that weighs 9.85 g and has a volume of 0.675 cm³. The jewelry contains only gold and silver, which have densities of 19.3 g/cm³ and 10.5 g/cm³, respectively. If the total volume of the jewelry is the sum of the volumes of the gold and silver that it contains, calculate the percentage of gold (by mass) in the jewelry. (b) The relative amount of gold in an alloy is commonly expressed in units of carats. Pure gold is 24 carat, and the percentage of gold in an alloy is given as a percentage of this value. For example, an alloy that is 50% gold is 12 carat. State the purity of the gold jewelry in carats.

1.79 Chromatography (Figure 1.14) is a simple but reliable method for separating a mixture into its constituent substances. You have a mixture of two vegetable dyes, one red and one blue, that you are trying to separate. You try two different chromatography procedures and achieve the separations shown in the figure. Which procedure worked better? Can you suggest a method to quantify how good or poor the separation was?

1.80 You are assigned the task of separating a desired granular material with a density of 3.62 g/cm³ from an undesired granular material that has a density of 2.04 g/cm³. You want to do this by shaking the mixture in a liquid in which the heavier material will fall to the bottom and the lighter material will float. A solid will float on any liquid that is more dense. Using the Internet or a handbook of chemistry, find the densities of the following substances: carbon tetrachloride, hexane, benzene, and diiodomethane. Which of these liquids will serve your purpose, assuming no chemical interaction between the liquid and the solids?

1.81 In 2009, a team from Northwestern University and Western Washington University reported the preparation of a new “spongy” material composed of nickel, molybdenum, and sulfur that excels at removing mercury from water. The density of this new material is 0.20 g/cm³, and its surface area is 1242 m² per gram of material. (a) Calculate the volume of a 10.0-mg sample of this material. (b) Calculate the surface area for a 10.0-mg sample of this material. (c) A 10.0-mL sample of contaminated water had 7.748 mg of mercury in it. After treatment with 10.0 mg of the new spongy material, 0.001 mg of mercury remained in the contaminated water. What percentage of the mercury was removed from the water? (d) What is the final mass of the spongy material after the exposure to mercury?

1.82 The concepts of accuracy and precision are not always easy to grasp. Here are two sets of studies: (a) The mass of a secondary weight standard is determined by weighing it on a very precise balance under carefully controlled laboratory conditions. The average of 18 different weight measurements is taken as the weight of the standard. (b) A group of 10,000 males between the ages of 50 and 55 is surveyed to ascertain a relationship between calorie intake and blood cholesterol level. The survey questionnaire is quite detailed, asking the respondents about what they eat, smoke, drink, and so on. The results are reported as showing that for men of comparable lifestyles, there is a 40% chance of the blood cholesterol level being above 230 mg/dL for those who consume more than 40 calories per gram of body weight per day, as compared with those who consume fewer than 30 calories per gram of body weight per day.

Discuss and compare these two studies in terms of the precision and accuracy of the result in each case. How do the two studies differ in ways that affect the accuracy and precision of the results? What makes for high precision and accuracy in any given study? In each of these studies, what factors might not be controlled that could affect the accuracy and precision? What steps can be taken generally to attain higher precision and accuracy?