Chemistry Essentials for Dummies
Chapter 9. Measuring Substances with the Mole
Moles: Putting Aoogadro's Number to Good Use
When people deal with objects, they often think in terms of a convenient amount. For example, when a woman buys earrings, she normally buys a pair of them. When a man goes to the grocery store, he buys eggs by the dozen. Likewise, when chemists deal with atoms and molecules, they need a convenient unit that takes into consideration the very small size of atoms and molecules. They use a unit called the mole.
Defining the mole
REMEMBER. The world mole stands for a number — approximately 6.022 x 1023. It’s commonly called Avogadro’s number, named for Amedeo Avogadro, the scientist who laid the groundwork for the mole principle.
Now a mole — 6.022 x 1023 — is a really big number. When written in longhand notation, it’s
602,200,000,000,000,000,000,000
And that is why I like scientific notation. (If you had a mole of marshmallows, it’d cover the United States to a depth of about 600 miles. A mole of rice grains would cover the land area of the world to a depth of about 75 meters.)
Avogadro’s number stands for a certain number of things. Normally, those things are atoms and molecules. So the mole relates to the microscopic world of atoms and molecules. But how does it relate to the macroscopic world where you work?
REMEMBER. The answer is that a mole (abbreviated as mol) is equal to the following:
✓ For carbon: A mole is the number of atoms in exactly 12 grams of C-12, a particular isotope of carbon. So if you have exactly 12 grams of 12C, you have 6.022 x 1023 carbon atoms, which is also a mole of 12C atoms.
✓ For any other element: A mole is the atomic weight using grams instead of atomic mass units.
✓ For a compound: For a compound, a mole is the formula (or molecular) weight in grams instead of atomic mass units.
Calculating Weight, particles, and moles
The mole is the bridge between the microscopic and macroscopic world:
6.022 x 1023 particles ↔ 1 mole ↔ atomic/formula weight in grams
If you have any one of the three things — particles, moles, or grams — then you can calculate the other two.
For example, the weight of a water molecule is 18.015 amu. Because a mole is the formula (or molecular) weight in grams of a compound, you can now say that the weight of a mole of water is 18.015 grams. You can also say that 18.015 grams of water contains 6.022 x 1023 H2O molecules, or a mole of water. And the mole of water is composed of two moles of hydrogen and one mole of oxygen.
Suppose you want to know how many water molecules are in 5.50 moles of water. You can set up a problem like this:
5.50 mol x 6.022 x 1023 molecules/mol = 3.31 x 1024 molecules
Or suppose that you want to know how many moles are in 25.0 grams of water. You can set up the problem like this:
![]()
You can even go from grams to particles by going through the mole. For example, how many molecules are in 100.0 grams of carbon dioxide? The first thing you have to do is determine the molecular weight of CO2. Look at the periodic table to find that one carbon atom equals 12.011 amu and one oxygen atom weighs 15.000 amu. Now figure the molecular weight, like this:
[(1 x 12.011 g/mol) + (2 x 15.999 g/mol)] = 44.01 g/mol for CO2
Now you can work the problem:

And going from particles to moles to grams is just as easy.
Finding formulas of compounds
You can use the mole concept to calculate the empirical formula of a compound using the percentage composition data for that compound — the percentage by weight of each element in the compound. (The empirical formula indicates the different types of elements in a molecule and the lowest whole-number ratio of each kind of atom in the molecule. See Chapter 6 for details.)
When I try to determine the empirical formula of a compound, I often have percentage data available. The determination of the percentage composition is one of the first analyses that a chemist does in learning about a new compound. Here’s how to find an empirical formula using moles and the percentages of each element:
1. Assume you have 100 grams of the compound so you can use the percentages as weights; then convert the weight of each element to moles.
For example, suppose you determine that a particular compound has the following weight percentage of elements present: 26.4 percent Na, 36.8 percent S, and 36.8 percent O. Because you’re dealing with percentage data (amount per hundred), assume that you have 100 grams of the compound so you can write the percentages as weights. Then convert each mass to moles, like this:
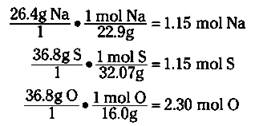
2. Write the empirical formula, changing subscripts to whole numbers if necessary.
Now you can write an empirical formula of Na1.15S1.15O2.30. Your subscripts have to be whole numbers, so divide each of these by the smallest, 1.15, to get NaSO2. (If a subscript is 1, it’s not shown.)
You can then calculate a weight for the empirical formula by adding together the atomic masses on the periodic table of one sodium (Na), one sulfur (S) and two oxygen (O). This gives you an empirical formula weight of 87.056 grams.