MCAT General Chemistry Review

Chapter 5: Chemical Kinetics

5.1 Chemical Kinetics

Reactions can be spontaneous or nonspontaneous; the change in Gibbs free energy (ΔG) determines whether or not a reaction will occur by itself without outside assistance. However, even if a reaction is spontaneous, this does not necessarily mean that it will run quickly. In fact, nearly every biochemical reaction that enables life to exist, while perhaps spontaneous, proceeds so slowly that, without the aid of enzymes and other catalysts, measurable reaction progress might not actually occur over the course of an average human lifetime. And enzymes, like many other catalyzed reactions, can be saturated and experience a maximal turnover rate, as shown in Figure 5.1. For now, however, let us review reaction mechanisms, rates, rate laws, and the factors that pertain to simple chemical systems.

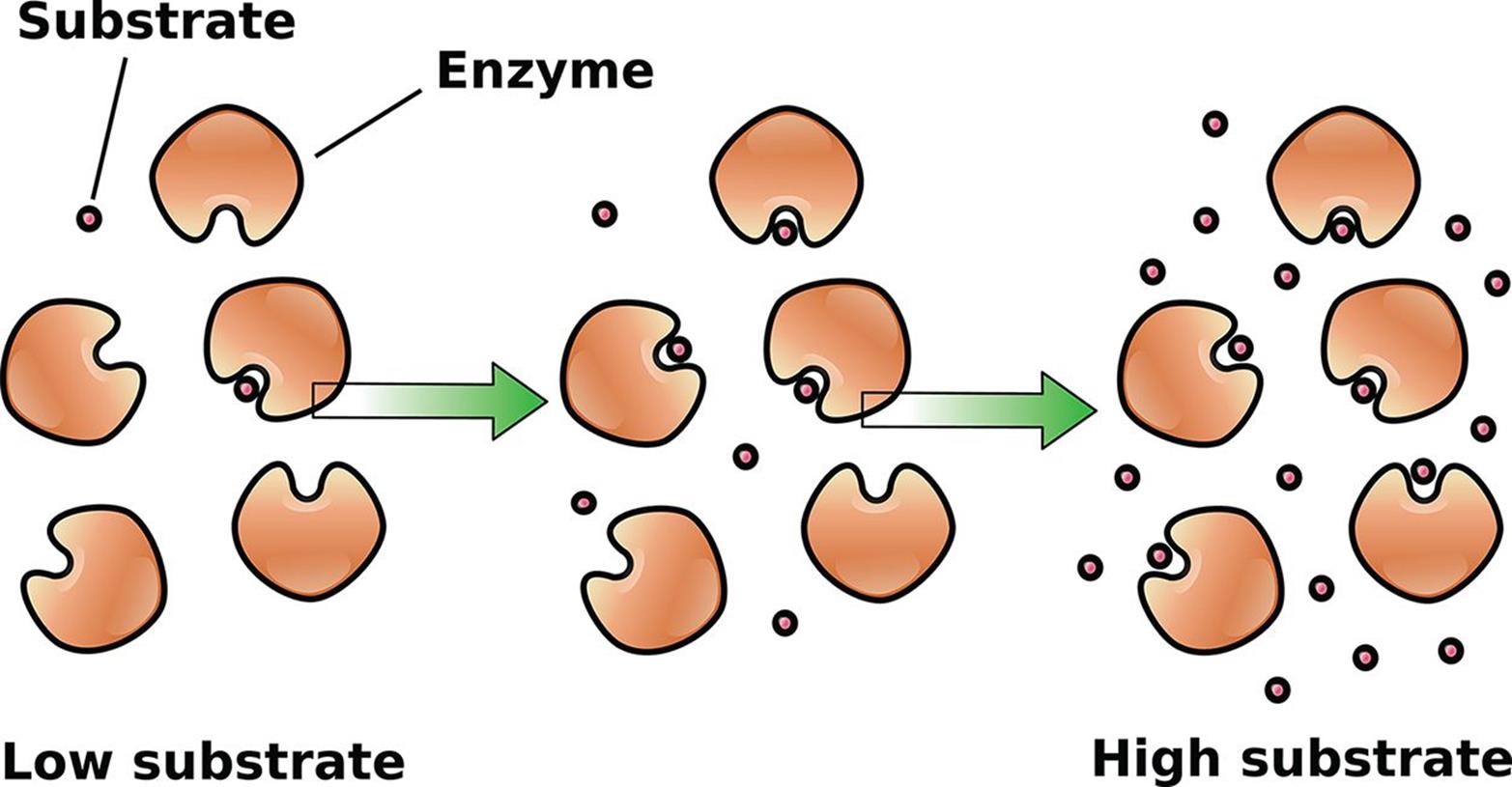Figure 5.1. Enyzmes, as Biological Catalysts, Can Be Saturated High substrate conditions saturate the active sites of the enzyme, leading to maximal turnover.

BRIDGE

Enzymes selectively enhance the rate of certain reactions by a factor of 10⁶ to 10¹⁴ over other thermodynamically feasible reaction pathways. Enzyme function is discussed in Chapter 2 of MCAT Biochemistry Review.

REACTION MECHANISMS

Very rarely is the balanced reaction equation, used for determining limiting reactants and yields, an accurate representation of the actual steps involved in the chemical process from reactants to products. Many reactions proceed by more than one step, the series of which is known as themechanism of a reaction, and the sum of which gives the overall reaction. Knowing the accepted mechanism of a reaction may help explain the reaction’s rate, position of equilibrium, and thermodynamic characteristics. Consider this generic reaction:

A₂ + 2 B → 2 AB

BRIDGE

Mechanisms are proposed pathways for a reaction that must coincide with rate data information from experimental observation. Reaction mechanisms are a major topic in organic chemistry and metabolism; Chapters 5 through 10 of MCAT Organic Chemistry Review and Chapters 9 through 12 of MCAT Biochemistry Review focus almost exclusively on reaction mechanisms in specific contexts.

On its own, this equation seems to imply a mechanism in which two molecules of B collide with one molecule of A₂ to form two molecules of AB. Suppose instead, however, that the reaction actually takes place in two steps:

Note that the two steps, taken together, give the overall net reaction. The molecule A₂B, which does not appear in the overall reaction, is called an intermediate. Reaction intermediates are often difficult to detect because they may be consumed almost immediately after they are formed, but a proposed mechanism that includes intermediates can be supported through kinetic experiments. One of the most important points to remember is that the slowest step in any proposed mechanism is called the rate-determining step because it acts like a kinetic bottleneck, preventing the overall reaction from proceeding any faster than that slowest step.

KEY CONCEPT

The rate of the whole reaction is only as fast as the rate-determining step.

MOLECULAR BASIS OF CHEMICAL REACTIONS

It’s one thing to say A₂ reacts with 2 B to form 2 AB; it’s quite another to be able to describe, as precisely as possible, the actual interactions that occur between A₂ and B to produce AB at some rate. Various theories have been proposed to explain the events that are taking place at the atomic level through the process of a reaction.

Collision Theory of Chemical Kinetics

For a reaction to occur, molecules must collide with each other. The collision theory of chemical kinetics states that the rate of a reaction is proportional to the number of collisions per second between the reacting molecules.

The theory suggests, however, that not all collisions result in a chemical reaction. An effective collision (one that leads to the formation of products) occurs only if the molecules collide with each other in the correct orientation and with sufficient energy to break their existing bonds and form new ones. The minimum energy of collision necessary for a reaction to take place is called the activation energy, Ea, or the energy barrier. Only a fraction of colliding particles have enough kinetic energy to exceed the activation energy. This means that only a fraction of all collisions are effective. The rate of a reaction can therefore be expressed as follows:

rate = Z × f

Equation 5.1

where Z is the total number of collisions occurring per second and f is the fraction of collisions that are effective. A much more quantitatively rigorous analysis of the collision theory can be applied through the Arrhenius equation which is normally given as:

Equation 5.2

where k is the rate constant of a reaction, A is the frequency factor, E_a is the activation energy of the reaction, R is the ideal gas constant, and T is the temperature in kelvins. The frequency factor, also known as the attempt frequency of the reaction, is a measure of how often molecules in a certain reaction collide, with the unit s^–1. Activation energy is a subject that will be touched upon briefly in the following subsection and more qualitatively in future chapters.

Overall, what is important here in studying the Arrhenius equation is not the actual calculation (because those involving Euler’s number, e, and natural logs, ln, are not commonly found on the MCAT), but rather the relationships between the variables and the exponent rules that govern the equation.

For example, a simple relationship between A and k is evident in the equation. As the frequency factor of the reaction increases, the rate constant of the reaction also increases in a direct relationship. More complex relationships can also be seen in this equation. For example, if the temperature (T) of a chemical system were to increase to infinity, while all other variables are held constant, the value of the exponent would have a magnitude less than 1. However, before assuming that the rate constant is going to decrease as a result, note the presence of the negative sign. As the magnitude of the exponent gets smaller, it actually moves from a more negative value toward zero. The exponent thus becomes less negative (or more positive), which means that the rate constant actually increases. This should make sense conceptually because the rate of a reaction increases with temperature.

MCAT EXPERTISE

Low activation energy and high temperatures make the negative exponent of the Arrhenius equation smaller in magnitude and thus increase the rate constant k.

The frequency factor can be increased by increasing the number of molecules in a vessel. When there are more molecules, the opportunities for collision are increased, as shown in Figure 5.2.

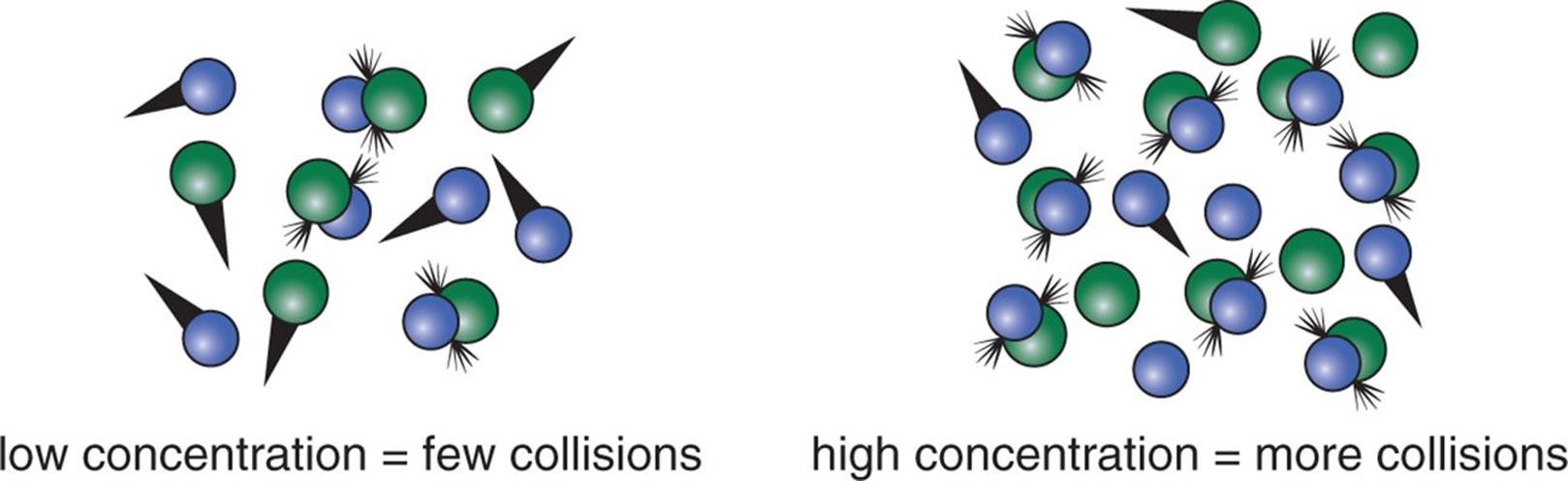Figure 5.2. Frequency Factor (A) Is Increased by Increasing Concentration

Transition State Theory

When molecules collide with energy equal to or greater than the activation energy, they form a transition state in which the old bonds are weakened and the new bonds begin to form. The transition state then dissociates into products, fully forming the new bonds. For the reaction A₂ + 2 B → 2 AB, the progress along the reaction coordinate, which traces the reaction from reactants to products, can be represented as shown in Figure 5.3.

Figure 5.3. The Transition State

The transition state, also called the activated complex, has greater energy than both the reactants and the products and is denoted by the symbol ‡. The energy required to reach this transition state is the activation energy. Once an activated complex is formed, it can either dissociate into the products or revert to reactants without any additional energy input. Transition states are distinguished from reaction intermediates in that transition states are theoretical constructs that exist at the point of maximum energy, rather than distinct identities with finite lifetimes.

KEY CONCEPT

Relative to reactants and products, transition states have the highest energy. They are only theoretical structures and cannot be isolated. Nevertheless, we can still use the proposed structures to better understand the reactions in which they are involved.

A free energy diagram illustrates the relationship between the activation energy, the free energy of the reaction, and the free energy of the system. The most important features to recognize in such diagrams are the relative energies of all of the products and reactants. The free energy change of the reaction (ΔGrxn) is the difference between the free energy of the products and the free energy of the reactants. A negative free energy change indicates an exergonic reaction (energy is given off), and a positive free energy change indicates an endergonic reaction (energy is absorbed). The transition state exists at the peak of the energy diagram. The difference in free energy between the transition state and the reactants is the activation energy of the forward reaction; the difference in free energy between the transition state and the products is the activation energy of the reverse reaction.

KEY CONCEPT

· +ΔG = endergonic = energy absorbed

· –ΔG = exergonic = energy given off

For example, consider the formation of HCl from H₂ and Cl₂. The overall reaction is:

H₂ (g) + Cl₂ (g) ⇌ 2 HCl (g)

Figure 5.4 shows that the reaction is exergonic. The free energy of the products is less than the free energy of the reactants; energy is released, and the free energy change of the reaction is negative.

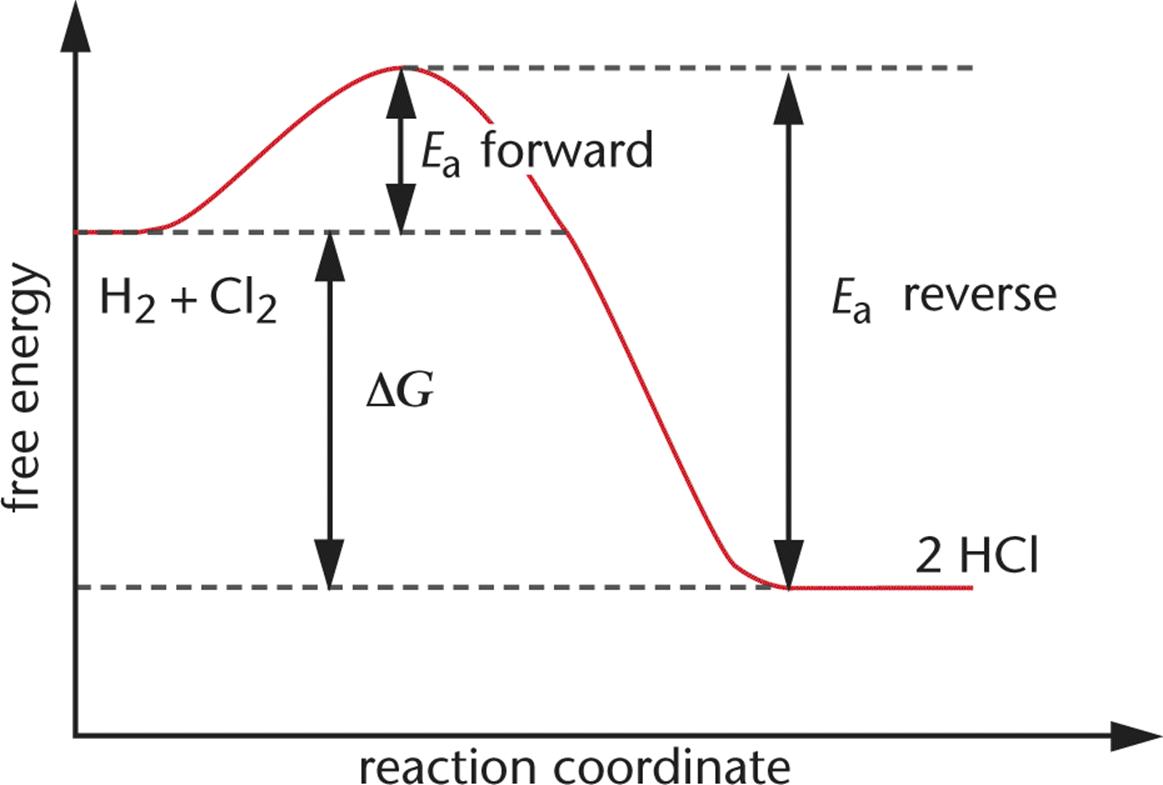Figure 5.4. Reaction Diagram for the Formation of HCl On the left are the reactants (H₂ and Cl₂) and on the right are the products (2 HCl); this reaction is exergonic, and forward and reverse activation energies are shown.

MCAT EXPERTISE

Kinetics and thermodynamics should be considered separately. Note that the free energy of the product can be raised or lowered, thereby changing the value of ΔG without affecting the value of forward E_a.

FACTORS AFFECTING REACTION RATE

Before we delve into the specifics of rate calculations, it is helpful to understand the conditions that can alter experimental rates.

Reaction Concentrations

The greater the concentrations of the reactants, the greater the number of effective collisions per unit time. Recall that this leads to an increase in the frequency factor (A) of the Arrhenius equation. Therefore, the reaction rate will increase for all but zero-order reactions, which will be discussed shortly. For reactions occurring in the gaseous state, the partial pressures of the gas reactants serve as a measure of concentration, as discussed in Chapter 8 of MCAT General Chemistry Review.

Temperature

For nearly all reactions, the reaction rate will increase as the temperature increases. Because the temperature of a substance is a measure of the particles’ average kinetic energy, increasing the temperature increases the average kinetic energy of the molecules. Consequently, the proportion of reactants gaining enough energy to surpass E_a (and thus capable of undergoing reaction) increases with higher temperature. All reactions—even the nuclear reactions shown in Figure 5.5—are temperature-dependent and experience an optimal temperature for activity.

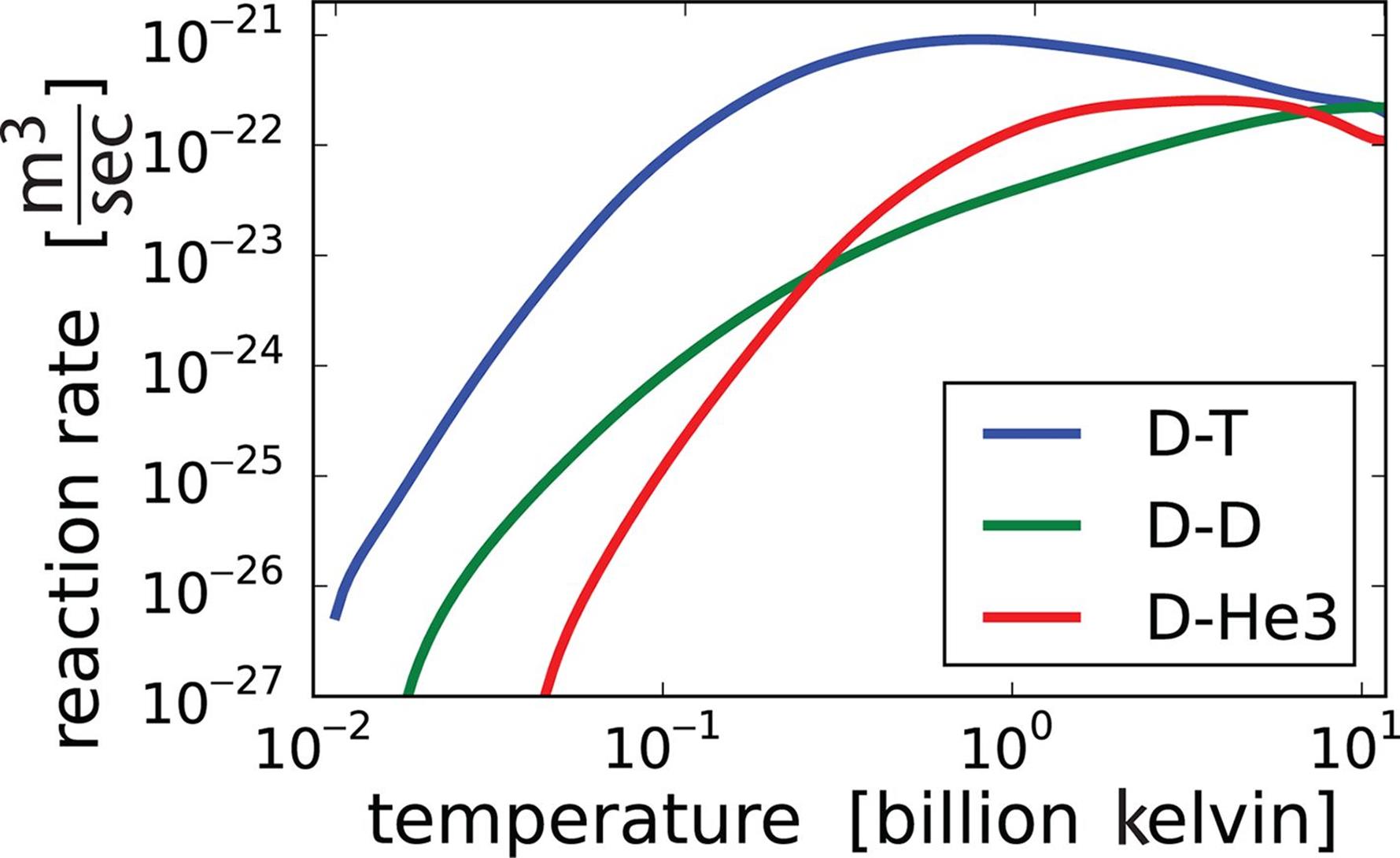Figure 5.5. All Reactions Are Temperature-Dependent Examples shown are nuclear fusion reactions; at extreme temperatures, the nucleus itself begins to break down.

You’ll often hear that raising the temperature of a system by 10°C will result in an approximate doubling of the reaction rate. Be careful with this approximation because it is generally true for biological systems but not so for many other systems. Further, even in biological systems, if the temperature gets too high, a catalyst may denature—and then the reaction rate plummets. Figure 5.6 shows a general curve for an enzymatic reaction that is optimal between 35°C and 40°C (body temperature). Notice that the curve falls sharply after 40°C, at which point denaturation has occurred.

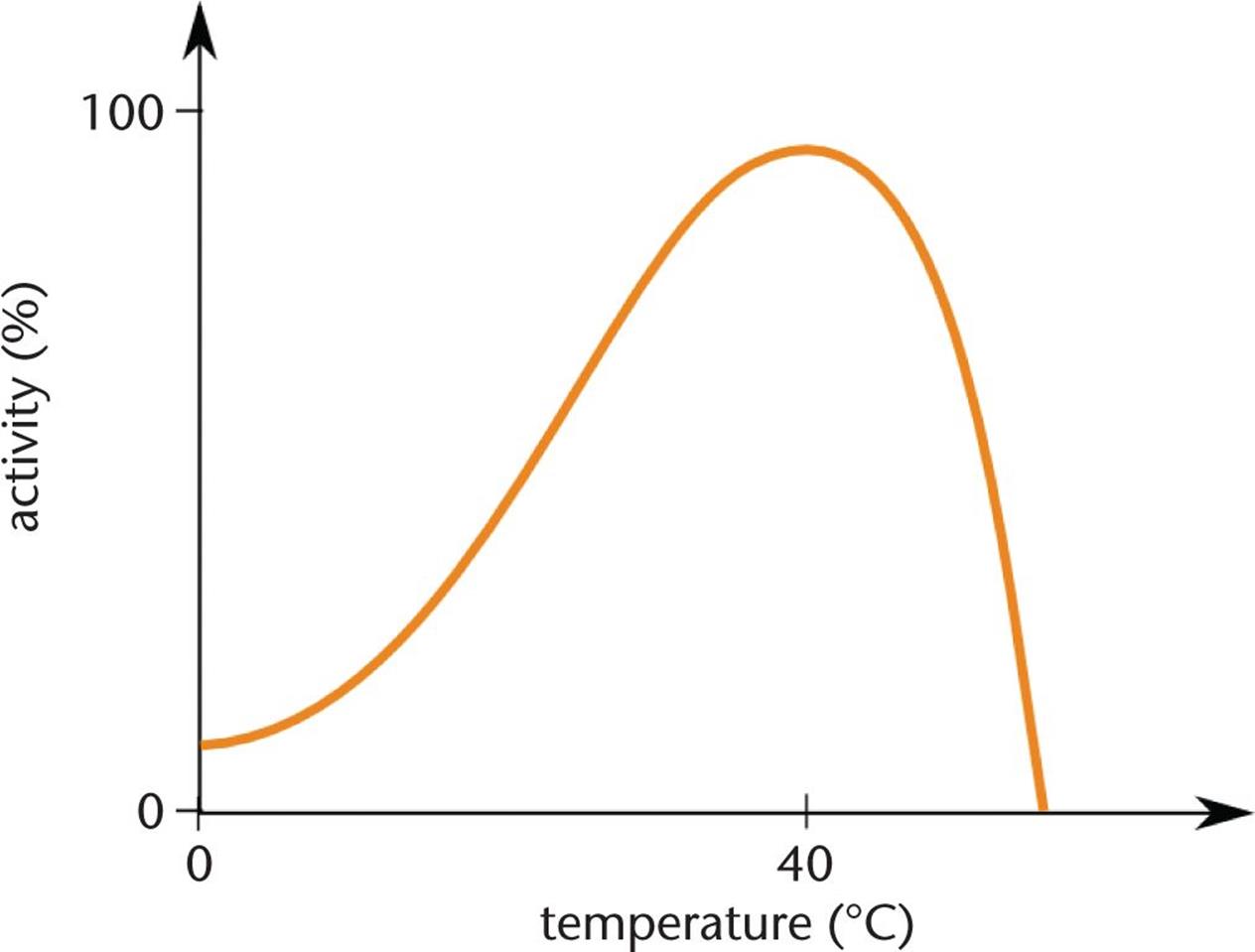Figure 5.6. An Activity vs. Temperature Curve for a Generic Human Enzyme

Medium

The rate at which a reaction takes place may also be affected by the medium in which it takes place. Some molecules are more likely to react with each other in aqueous environments, while others are more likely to react in nonaqueous solvents, such as in dimethyl sulfoxide (DMSO) or ethanol. Furthermore, the physical state of the medium (liquid, solid, or gas) can also have a significant effect. Generally, polar solvents are preferred because their molecular dipole tends to polarize the bonds of the reactants, thereby lengthening and weakening them, permitting the reaction to occur faster.

Catalysts

Catalysts are substances that increase reaction rate without themselves being consumed in the reaction. Catalysts interact with the reactants, either by adsorption or through the formation of intermediates, and stabilize them so as to reduce the activation energy necessary for the reaction to proceed. While many catalysts, including all enzymes, chemically interact with the reactants, they return to their original chemical state upon formation of the products. They may increase the frequency of collisions between the reactants; change the relative orientation of the reactants, making a higher percentage of the collisions effective; donate electron density to the reactants; or reduce intramolecular bonding within reactant molecules. In homogeneous catalysis, the catalyst is in the same phase (solid, liquid, gas) as the reactants. In heterogeneous catalysis, the catalyst is in a distinct phase. Figure 5.7 compares the energy profiles of catalyzed and uncatalyzed reactions.

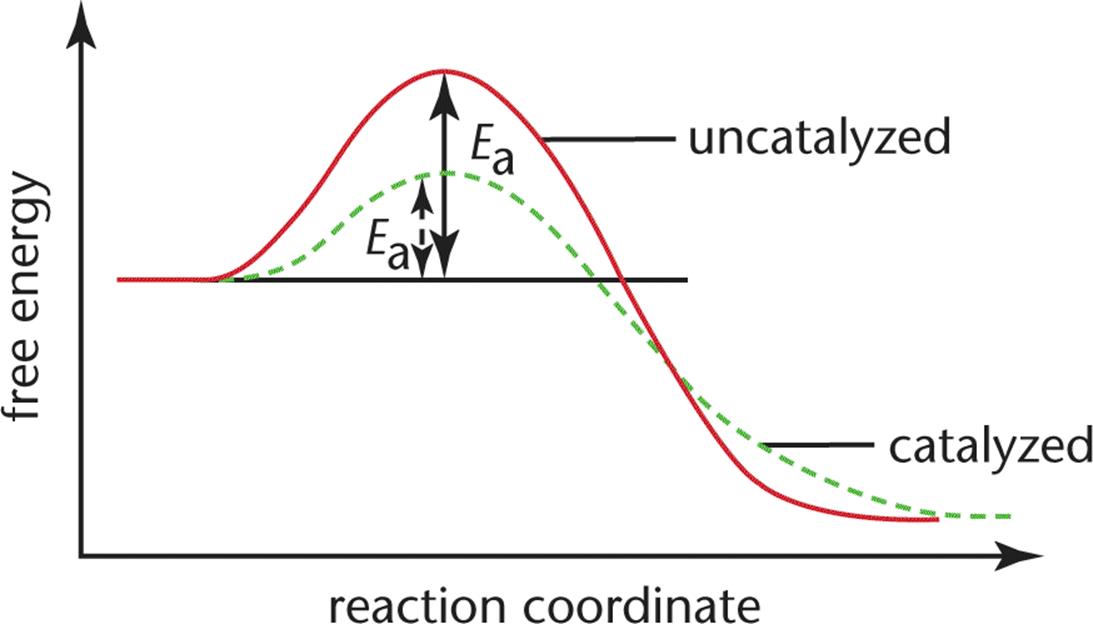Figure 5.7. Reaction Diagram for a Catalyzed and an Uncatalyzed Reaction

Notice that the only effect of the catalyst is the decrease in the energies of activation, E_a, for both the forward and reverse reactions. The presence of the catalyst has no impact on the free energies of the reactants or the products or the difference between them. This means that catalysts change only the rates of reactions, and in fact, change the forward rate and the reverse rate by the same factor. Consequently, they have no impact whatsoever on the equilibrium position or the measurement of K_eq. Remember that, as useful as catalysts are in biological and nonbiological systems, catalysts are not miracle workers: they will not transform a nonspontaneous reaction into a spontaneous one; they only make spontaneous reactions move more quickly toward equilibrium.

BRIDGE

Equilibrium, like biological homeostasis, is a dynamic process that seeks to find balance in all systems. We can use this concept to our advantage on the MCAT in all seven of the basic sciences. Equilibria are dynamic, meaning that they do undergo change but their net change will be zero.

MCAT Concept Check 5.1:

Before you move on, assess your understanding of the material with these questions.

1. Describe in words what is occurring in the following two step mechanism:

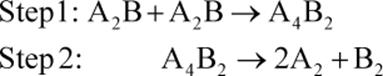
2. What does it mean for a step in a mechanism to be the rate-determining step?

3. What is activation energy?

4. How does the transition state theory compare with the collision theory of chemical kinetics?

· Transition state theory:

· Collision theory: