MCAT General Chemistry Review
Chapter 5: Chemical Kinetics
5.2 Reaction Rates
Reactions, unfortunately, do not come with handy built-in speedometers. To determine the rate at which a reaction proceeds, we must take measurements of the concentrations of reactants and products and note their change over time.
DEFINITION OF RATE
If we consider a generic reaction, 2 A + B → C, in which one mole of C can be produced from two moles of A and one mole of B, we can describe the rate of this reaction in terms of either the disappearance of reactants over time or the appearance of products over time. Because the reactants, by definition, are being consumed in the process of formation of the products, we place a negative sign in front of the rate expression for reactants. For the above reaction, the rate of the reaction with respect to A is ![]() with respect to B is
with respect to B is ![]() and with respect to C is
and with respect to C is ![]() Notice that the stoichiometric coefficients for the reaction are not equal, which means that the rates of change of concentrations are not equal. Because two moles of A are consumed for every mole of B consumed, rate–Δ[A] = 2 × rate–Δ[B]. Furthermore, for every two moles of A consumed, only one mole of C is produced; thus, we can say that the rate–Δ[A] = 2 × rateΔ[C]. Based on the stoichiometry, we can see that the rate of consumption of B is equal to the rate of production of C. To show a standard rate of reaction in which the rates with respect to all reaction species are equal, the rate of concentration change of each species should be divided by the species’ stoichiometric coefficients. Thus, for the general reaction aA + bB → cC + dD,
Notice that the stoichiometric coefficients for the reaction are not equal, which means that the rates of change of concentrations are not equal. Because two moles of A are consumed for every mole of B consumed, rate–Δ[A] = 2 × rate–Δ[B]. Furthermore, for every two moles of A consumed, only one mole of C is produced; thus, we can say that the rate–Δ[A] = 2 × rateΔ[C]. Based on the stoichiometry, we can see that the rate of consumption of B is equal to the rate of production of C. To show a standard rate of reaction in which the rates with respect to all reaction species are equal, the rate of concentration change of each species should be divided by the species’ stoichiometric coefficients. Thus, for the general reaction aA + bB → cC + dD,
![]()
Equation 5.3
Rate is expressed in the units of moles per liter per second 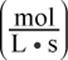 or molarity per second
or molarity per second 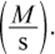
DETERMINATION OF RATE LAW
In the Chemical and Physical Foundations of Biological Systems section of the MCAT, it is unlikely that the testmakers will provide a reaction equation that one can merely look at and write the correct rate law. Therefore, on the MCAT, whenever a question asks to determine the rate law for a reaction, the first thing to look for is experimental data.
MCAT EXPERTISE
Remember that the stoichiometric coefficients for the overall reaction are often different from those for the rate law and will, therefore, not be the same as the order of the reaction.
For nearly all forward, irreversible reactions, the rate is proportional to the concentrations of the reactants, with each concentration raised to some experimentally determined exponent. For the general reaction
aA + bB → cC + dD
the rate is proportional to [A]x[B]y. By including a proportionality constant, k, we can say that rate is determined according to the following equation:
rate = k[A]x[B]y
Equation 5.4
where k is the reaction rate coefficient or rate constant and the exponents x and y are the orders of the reaction. This expression is called the rate law. Remember that rate is always measured in units of concentration over time; that is, molarity per second. The exponents x and y (or x, y, andz, if there are three reactants) can be used to state the order of the reaction with respect to each reactant or overall: x is the order with respect to reactant A, and y is order with respect to reactant B. The overall order of the reaction is the sum of x and y. These exponents may be integers or fractions and must be determined experimentally. The MCAT will focus almost exclusively on zero-, first-, second-, and third-order reactions. In most cases, the exponents will be integers.
Before we go any further in our consideration of rate laws, we must offer a few warnings about common traps in chemical kinetics. The first—and most common—is the assumption that the orders of a reaction are the same as the stoichiometric coefficients in the balanced overall equation. Pay close attention: On the MCAT, the values of x and y are almost never the same as the stoichiometric coefficients. The orders of a reaction must be determined experimentally. There are only two cases in which the stoichiometric coefficients match the orders of the reaction. The first is when the reaction mechanism is a single step and the balanced overall reaction is reflective of the entire chemical process. The second is when the complete reaction mechanism is given and the rate-determining step is indicated. The stoichiometric coefficients on the reactant side of the rate-determining step are equal to the orders of the reaction. Occasionally, even this can get a little complicated when the rate-determining step involves an intermediate as a reactant, in which case one must derive the intermediate molecule’s concentration by the law of mass action (that is, the equilibrium constant expression) for the step that produced the intermediate.
MCAT EXPERTISE
Note that the exponents in the rate law are not equal to the stoichiometric coefficients, unless the reaction occurs via a single-step mechanism. Note that product concentrations never appear in a rate law. Don’t fall into the exceedingly common trap of confusing the rate law with an equilibrium expression!
The second common trap is mistaking the equilibrium constant expression (law of mass action) for the rate law. The expressions for both look similar; if you’re not alert on Test Day, you may mistake one for the other or use one when you should be using the other. The expression for equilibrium includes the concentrations of all the species in the reaction, both reactants and products. The expression for chemical kinetics—the rate law expression—includes only the reactants. Keq indicates where the reaction’s equilibrium position lies. The rate indicates how quickly the reaction will get there.
The third trap regards the rate constant, k. Technically speaking, k is not a constant because its particular value for any specific chemical reaction will depend on the activation energy for that reaction and the temperature at which the reaction takes place. However, for a specific reaction, at a specific temperature, the rate constant is indeed a constant. For a reversible reaction, the Keq is equal to the ratio of the rate constant for the forward reaction, k, divided by the rate constant for the reverse reaction, k–1.
The fourth and final trap is that the notion and principles of equilibrium apply to the system only at the end of the reaction; that is, after the system has already reached equilibrium. On the other hand, while the reaction rate can theoretically be measured at any time, it is usually measured at or near the beginning of the reaction to minimize the effects of the reverse reaction.
Experimental Determination of Rate Law
This has already been stated a few times, but it bears repeating: The values of k, x, and y in the rate law equation (rate = k[A]x[B]y) must be determined experimentally for a given reaction at a given temperature. Although rate laws can be quite complex and the orders of the reaction difficult to discern, the MCAT limits its coverage of this topic to fairly straightforward reaction mechanisms, experimental data, and rate laws.
On the MCAT, experimental data for determining rate order is usually provided as a chart that includes the initial concentrations of the reactants and the initial rates of product formation as a function of the reactant concentrations. Often, the data for three or four trials are included in this chart.
To use this data, identify a pair of trials in which the concentration of one of the reactants is changed while the concentrations of all other reactants remain constant. Under these conditions, any change in the rate of product formation from one trial to the other (if there is any change) is fully attributable to the change in concentration of that one reactant. Consider a reaction with two reactants, A and B, forming product C. Imagine two trials in which the concentration of A is constant, while the concentration of B doubles. If the rate of the formation of product C has subsequently quadrupled, then the exponent on [B] must be two. Why? Looking at the generic rate law (rate = k[A]x[B]y), the logic should look something like this: Doubling [B] has resulted in a quadrupling of the rate, so to determine the order of the reaction, y, with respect to B, I need to calculate the exponent to which the number 2 must be raised to equal 4. Because 2y = 4, y = 2.
MCAT EXPERTISE
The testmakers love rate problems. Why? Because solving these questions requires a real understanding of proportionality and variable relationships. With practice, you’ll be able to do these quickly in your head with minimal paper-and-pencil calculations. Remember to look for pairs of reaction trials in which the concentration of only one species changes while the others remain constant.
The next step is to repeat this process for the other reactant, using data from a different pair of trials, making sure that the concentration of only the reactant we are trying to analyze is changed from one trial to the other while the concentrations of all other reactants remain the same. Once the orders of the reaction have been determined with respect to each reactant, we can write the complete rate law, replacing the exponents x and y with actual numbers. To determine the value of the rate constant k, plug in actual values from any one of the trials; pick whichever trial has the most arithmetically convenient numbers.
Example:
Given the data below, find the rate law for the following reaction at 300 K:
A + B → C + D
|
Trial |
[A]initial (M) |
[B]initial (M) |
|
|
1 |
1.00 |
1.00 |
2.0 |
|
2 |
1.00 |
2.00 |
8.1 |
|
3 |
2.00 |
2.00 |
15.9 |
Solution:
First, look for two trials in which the concentrations of all but one of the substances are held constant.
In Trials 1 and 2, the concentration of A is kept constant, while the concentration of B is doubled. The rate increases by a factor of approximately 4. Considering that k and [A] are constant between the two trials, we have set up a system where rate is proportional to [B] raised to some power (remember that the symbol means “is proportional to”):
![]()
If the rate was multiplied by 4, and [B] was multiplied by 2, this implies the expression 4 = 2y. y is therefore equal to 2.
In Trials 2 and 3, the concentration of B is kept constant, while the concentration of A is doubled. The rate increases by a factor of approximately 2. Considering that k and [B] are constant between the two trials, we have set up a system where rate is proportional to [A] raised to some power:
![]()
If the rate was multiplied by 2, and [A] was multiplied by 2, this implies the expression 2 = 2x. x is therefore equal to 1.
Therefore, rate = k[A][B]2. The order of the reaction with respect to A is 1 and with respect to B is 2; the overall reaction order is 1 + 2 = 3.
To calculate k, substitute the values from any one of the above trials into the rate law:
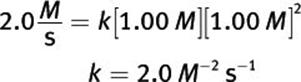
Therefore, the rate law is rate = 2.0 M–2 s–1 [A][B]2
REACTION ORDERS
We classify chemical reactions as zero-order, first-order, second-order, higher-order, or mixed-order on the basis of kinetics. We will continue to consider the generic reaction aA + bB → cC + dD for this discussion.
Zero-Order Reaction
A zero-order reaction is one in which the rate of formation of product C is independent of changes in concentrations of any of the reactants, A and B. These reactions have a constant reaction rate equal to the rate constant (rate coefficient), k. The rate law for a zero-order reaction is:
rate = k[A]0[B]0 = k
where k has units of ![]() Remember that the rate constant itself is dependent on temperature; thus, it is possible to change the rate for a zero-order reaction by changing the temperature. The only other way to change the rate of a zero-order reaction is by the addition of a catalyst, which lowers the activation energy, thereby increasing the value of k.
Remember that the rate constant itself is dependent on temperature; thus, it is possible to change the rate for a zero-order reaction by changing the temperature. The only other way to change the rate of a zero-order reaction is by the addition of a catalyst, which lowers the activation energy, thereby increasing the value of k.
MCAT EXPERTISE
Temperature and the addition of a catalyst are the only factors that can change the rate of a zero-order reaction.
Plotting a zero-order reaction on a concentration vs. time curve results in a linear graph, as shown in Figure 5.8. This line shows that the rate of formation of product is independent of the concentration of reactant. The slope of such a line is the opposite of the rate constant, k.
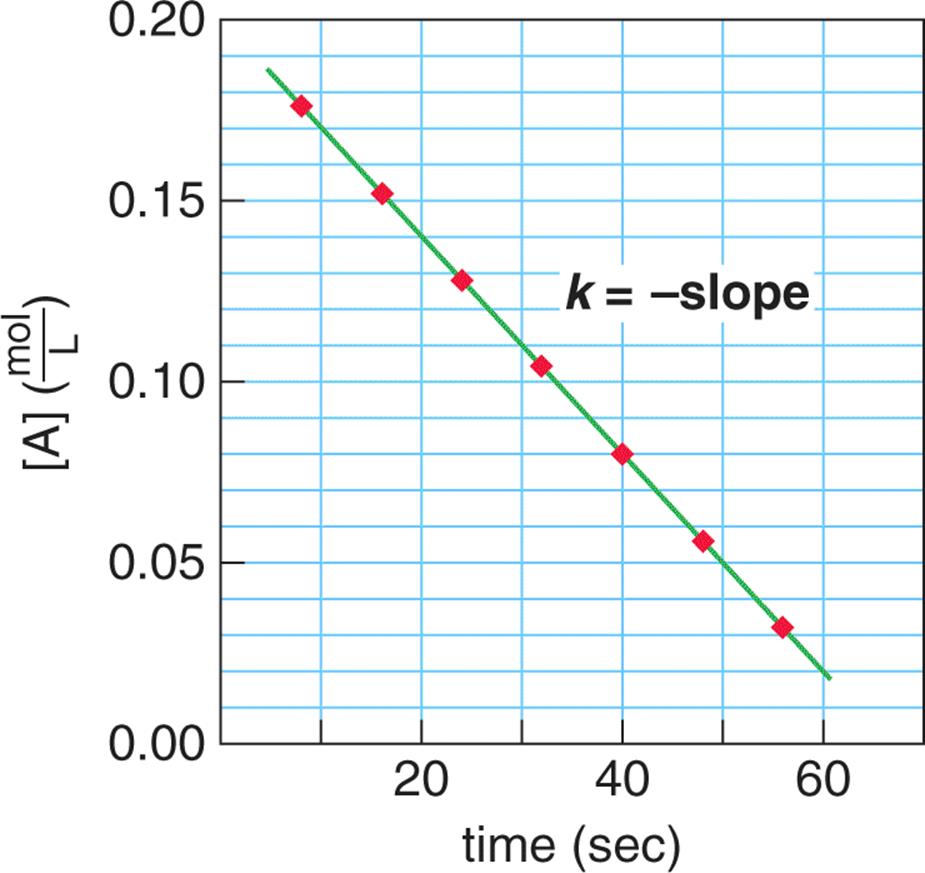 Figure 5.8. Kinetics of a Zero-Order Reaction Note that the rate of reaction, k, is the opposite of the slope.
Figure 5.8. Kinetics of a Zero-Order Reaction Note that the rate of reaction, k, is the opposite of the slope.
First-Order Reaction
A first-order reaction has a rate that is directly proportional to only one reactant, such that doubling the concentration of that reactant results in a doubling of the rate of formation of the product. The rate law for a first-order reaction is
rate = k[A]1 or rate = k[B]1
where k has units of s–1. A classic example of a first-order reaction is the process of radioactive decay. From the rate law, in which the rate of decrease of the amount of a radioactive isotope A is proportional to the amount of A,
![]()
The concentration of radioactive substance A at any time t can be expressed mathematically as:
[A]t = [A]0e–kt
Equation 5.5
where [A]t is the concentration of A at time t, [A]0 is the initial concentration of A, k is the rate constant, and t is time. It is important to recognize that a first-order rate law with a single reactant suggests that the reaction begins when the molecule undergoes a chemical change all by itself, without a chemical interaction, and usually without a physical interaction with any other molecule.
Plotting a first-order reaction on a concentration vs. time curve results in a nonlinear graph, as shown in Figure 5.9. This curve shows that the rate of formation of product is dependent on the concentration of reactant. Plotting ln [A] vs. time reveals a straight line; the slope of such a line is the opposite of the rate constant, k.
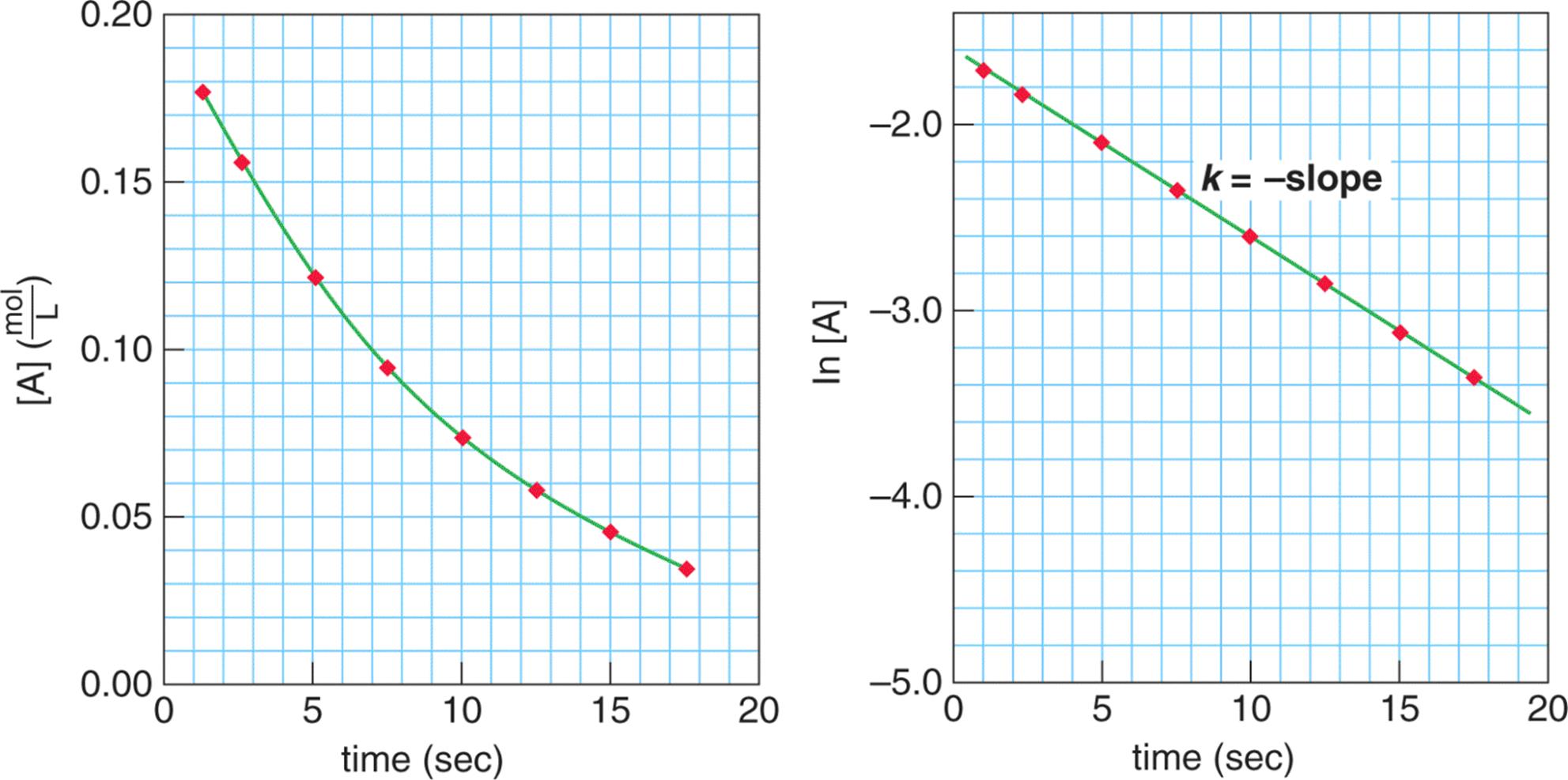 Figure 5.9. Kinetics of a First-Order Reaction On the left, note that the rate of reaction is dependent on reactant concentration; on the right, note that the rate constant is the opposite of the slope of a graph of ln [A] vs. time.
Figure 5.9. Kinetics of a First-Order Reaction On the left, note that the rate of reaction is dependent on reactant concentration; on the right, note that the rate constant is the opposite of the slope of a graph of ln [A] vs. time.
Second-Order Reaction
A second-order reaction has a rate that is proportional to either the concentrations of two reactants or to the square of the concentration of a single reactant. The following rate laws all reflect second-order reactions:
rate = k[A]1[B]1 or rate = k[A]2 or rate = k[B]2
where k has units of M–1 s–1. It is important to recognize that a second-order rate law often suggests a physical collision between two reactant molecules, especially if the rate law is first-order with respect to each of the two reactants.
Plotting a reaction that is second-order with respect to a single reactant on a concentration vs. time curve results in a nonlinear graph, as shown in Figure 5.10. This curve shows that the rate of formation of product is dependent on the concentration of reactant. Plotting ![]() vs. time reveals a linear curve; the slope of such a curve is equal to the rate constant, k.
vs. time reveals a linear curve; the slope of such a curve is equal to the rate constant, k.
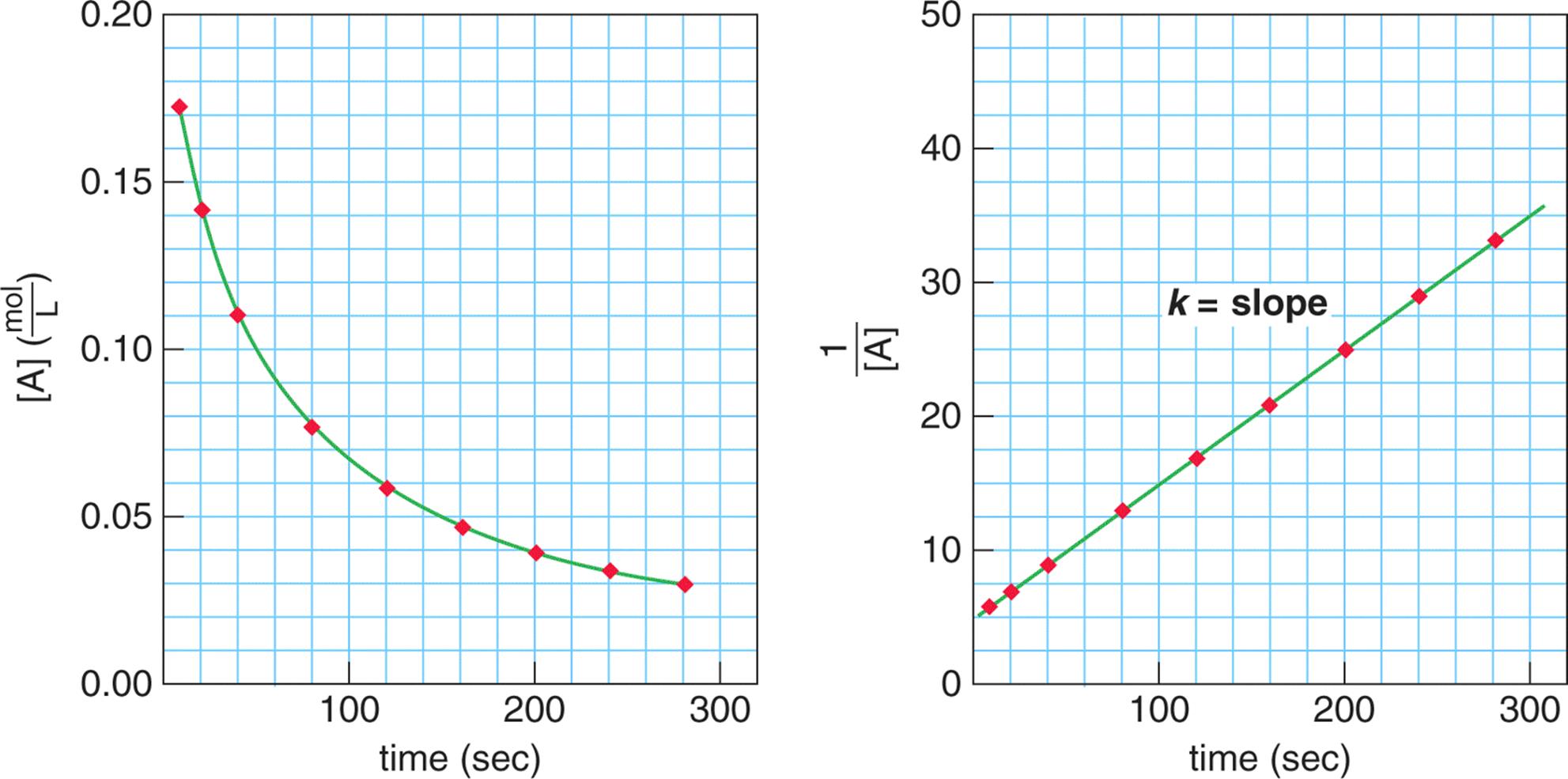 Figure 5.10. Kinetics of a Second-Order Reaction On the left, note that the rate of reaction is dependent on reactant concentration; on the right, note that the rate constant is equal to the slope of a graph of
Figure 5.10. Kinetics of a Second-Order Reaction On the left, note that the rate of reaction is dependent on reactant concentration; on the right, note that the rate constant is equal to the slope of a graph of ![]() vs. time.
vs. time.
Higher-Order Reactions
Fortunately there are very few noteworthy reactions in which a single reaction step involves a termolecular process; in other words, there are few processes with third-order rates. This is because it is far more rare for three particles to collide simultaneously with the correct orientation and sufficient energy to undergo a reaction.
Mixed-Order Reactions
Mixed-order reactions sometimes refer to non-integer orders (fractions) and in other cases to reactions with rate orders that vary over the course of the reaction. Fractions are more specifically described as broken-order. In recent times, the term mixed-order has come to refer solely to reactions that change order over time. Knowing those two definitions will be sufficient for Test Day.
An example of a mixed-order rate law is given by:
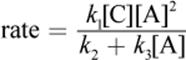
where A represents a single reactant and C, a catalyst. The overall reaction and its mechanism are beyond the relevance and scope of the MCAT, and the derivation of this rate law is even more unnecessary for Test Day. The result of the large value for [A] at the beginning of the reaction is that k3[A] >> k2, and the reaction will appear to be first-order with respect to A. At the end of the reaction, when [A] is low, k2 >> k3[A], making the reaction appear second-order with respect to A. While the MCAT will not ask you to derive a rate expression for a mixed-order reaction, you are responsible for being able to recognize how the rate order changes as the reactant concentration changes.
MCAT Concept Check 5.2:
Before you move on, assess your understanding of the material with these questions.
1. Describe the effects the following conditions would have on the initial rate of reaction, given the reaction order: (Examples: rate increased, rate divided by 2, rate unaffected)
|
Conditions |
Zero-Order |
First-Order |
Second-Order |
|
Temperature lowered |
|||
|
All reactants’ concentrations doubled |
|||
|
Catalyst added |
2. Determine the rate law and rate order for the following reaction:
A + B + C → D
|
Trial |
[A]initial (M) |
[B]initial (M) |
[C]initial (M) |
|
|
1 |
1.00 |
1.00 |
1.00 |
2.0 |
|
2 |
1.00 |
2.00 |
1.00 |
2.1 |
|
3 |
2.00 |
1.00 |
1.00 |
15.9 |
|
4 |
2.00 |
1.00 |
2.00 |
32.2 |

