MCAT General Chemistry Review
Chapter 1: Atomic Structure
1.4 Quantum Mechanical Model of Atoms
While Bohr’s model marked a significant advancement in the understanding of the structure of atoms, his model ultimately proved inadequate to explain the structure and behavior of atoms containing more than one electron. The model’s failure was a result of not taking into account the repulsion between multiple electrons surrounding the nucleus. Modern quantum mechanics has led to a more rigorous and generalizable study of the electronic structure of atoms. The most important difference between Bohr’s model and the modern quantum mechanical model is that Bohr postulated that electrons follow a clearly defined circular pathway or orbit at a fixed distance from the nucleus, whereas modern quantum mechanics has shown that this is not the case. Rather, we now understand that electrons move rapidly and are localized within regions of space around the nucleus called orbitals. The confidence by which those in Bohr’s time believed they could identify the location (or pathway) of the electron was now replaced by a more modest suggestion that the best we can do is describe the probability of finding an electron within a given region of space surrounding the nucleus. In the current quantum mechanical model, it is impossible to pinpoint exactly where an electron is at any given moment in time. This is expressed best by the Heisenberg uncertainty principle: It is impossible to simultaneously determine, with perfect accuracy, the momentum and the position of an electron. If we want to assess the position of an electron, the electron has to stop (thereby removing its momentum); if we want to assess its momentum, the electron has to be moving (thereby changing its position). This can be seen visually in Figure 1.8.
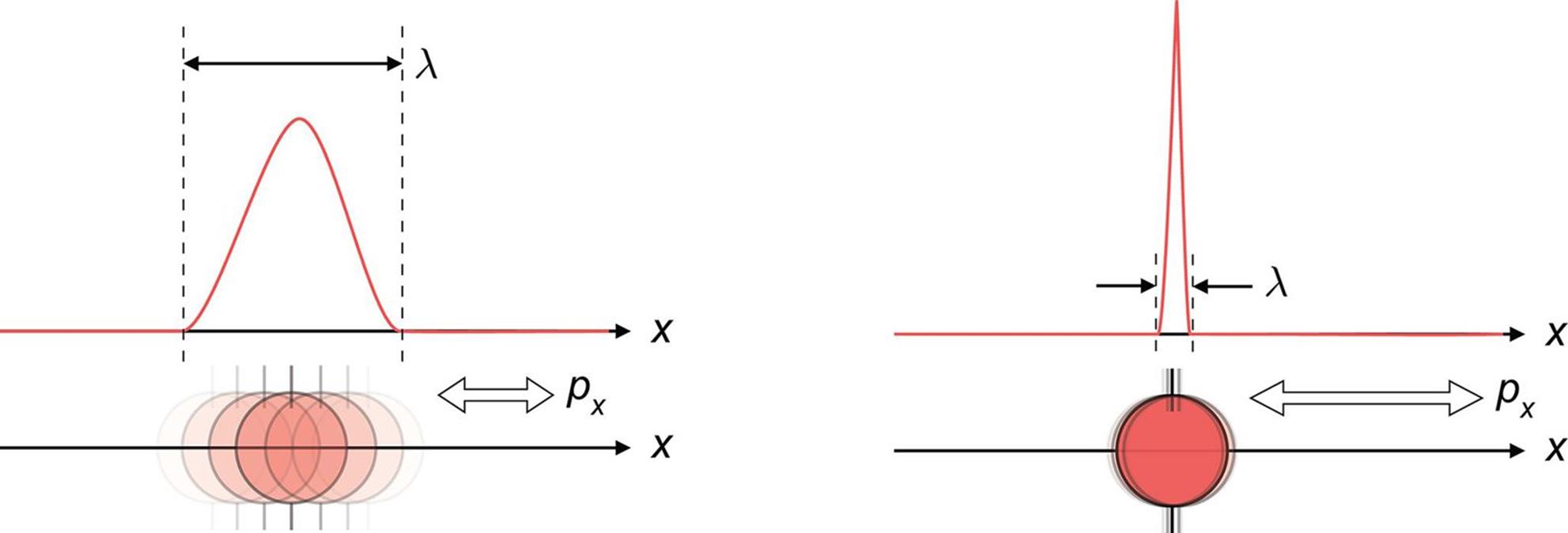 Figure 1.8. Heisenberg Uncertainty Principle Known momentum and uncertain position (left); known position but uncertain momentum (right). λ = confidence interval of position; px = confidence interval of momentum.
Figure 1.8. Heisenberg Uncertainty Principle Known momentum and uncertain position (left); known position but uncertain momentum (right). λ = confidence interval of position; px = confidence interval of momentum.
QUANTUM NUMBERS
Modern atomic theory postulates that any electron in an atom can be completely described by four quantum numbers: n, l, ml, and ms. Furthermore, according to the Pauli exclusion principle, no two electrons in a given atom can possess the same set of four quantum numbers. The position and energy of an electron described by its quantum numbers is known as its energy state. The value of n limits the values of l, which in turn limit the values of ml. In other words, for a given value of n, only particular values of l are permissible; given a value of l, only particular values of mlare permissible. The values of the quantum numbers qualitatively give information about the orientation of the orbitals. As we examine the four quantum numbers more closely, pay attention especially to l and ml because these two tend to give students the greatest difficulty.
MCAT EXPERTISE
Think of the quantum numbers as becoming more specific as one goes from n to l to ml to ms. This is like an address: one lives in a particular state (n), in a particular city (l), on a particular street (ml), at a particular house number (ms).
Principal Quantum Number
The first quantum number is commonly known as the principal quantum number and is denoted by the letter n. This is the quantum number used in Bohr’s model that can theoretically take on any positive integer value. The larger the integer value of n, the higher the energy level and radius of the electron’s shell. Within each shell, there is a capacity to hold a certain number of electrons, given by:
Maximum number of electrons within a shell = 2n2
Equation 1.6
where n is the principal quantum number. The difference in energy between two shells decreases as the distance from the nucleus increases because the energy difference is a function of 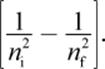 For example, the energy difference between the n = 3 and the n = 4 shells
For example, the energy difference between the n = 3 and the n = 4 shells 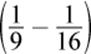 is less than the energy difference between the n = 1 and the
is less than the energy difference between the n = 1 and the 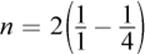 shells. This can be seen in Figure 1.7. Remember that electrons do not travel in precisely defined orbits; it just simplifies the visual representation of the electrons’ motion.
shells. This can be seen in Figure 1.7. Remember that electrons do not travel in precisely defined orbits; it just simplifies the visual representation of the electrons’ motion.
BRIDGE
Remember, a larger integer value for the principal quantum number indicates a larger radius and higher energy. This is similar to gravitational potential energy, as discussed in Chapter 2 of MCAT Physics Review, where the higher or farther the object is above the Earth, the higher its potential energy will be.
Azimuthal Quantum Number
The second quantum number is called the azimuthal (angular momentum) quantum number and is designated by the letter l. The second quantum number refers to the shape and number of subshells within a given principal energy level (shell). The azimuthal quantum number is very important because it has important implications for chemical bonding and bond angles. The value of n limits the value of l in the following way: for any given value of n, the range of possible values for l is 0 to (n – 1). For example, within the first principal energy level, n = 1, the only possible value for l is 0; within the second principal energy level, n = 2, the possible values for l are 0 and 1. A simpler way to remember this relationship is that the n-value also tells you the number of possible subshells. Therefore, there’s only one subshell (l = 0) in the first principal energy level; there are two subshells (l = 0 and 1) within the second principal energy level; there are three subshells (l = 0, 1, and 2) within the third principal energy level, and so on.
KEY CONCEPT
For any principal quantum number n, there will be n possible values for l, ranging from 0 to (n – 1).
Spectroscopic notation refers to the shorthand representation of the principal and azimuthal quantum numbers. The principal quantum number remains a number, but the azimuthal quantum number is designated by a letter: the l = 0 subshell is called s; the l = 1 subshell is called p; the l = 2subshell is called d; and the l = 3 subshell is called f. Thus, an electron in the shell n = 4 and subshell l = 2 is said to be in the 4d subshell. The spectroscopic notation for each subshell is demonstrated in Figure 1.9.
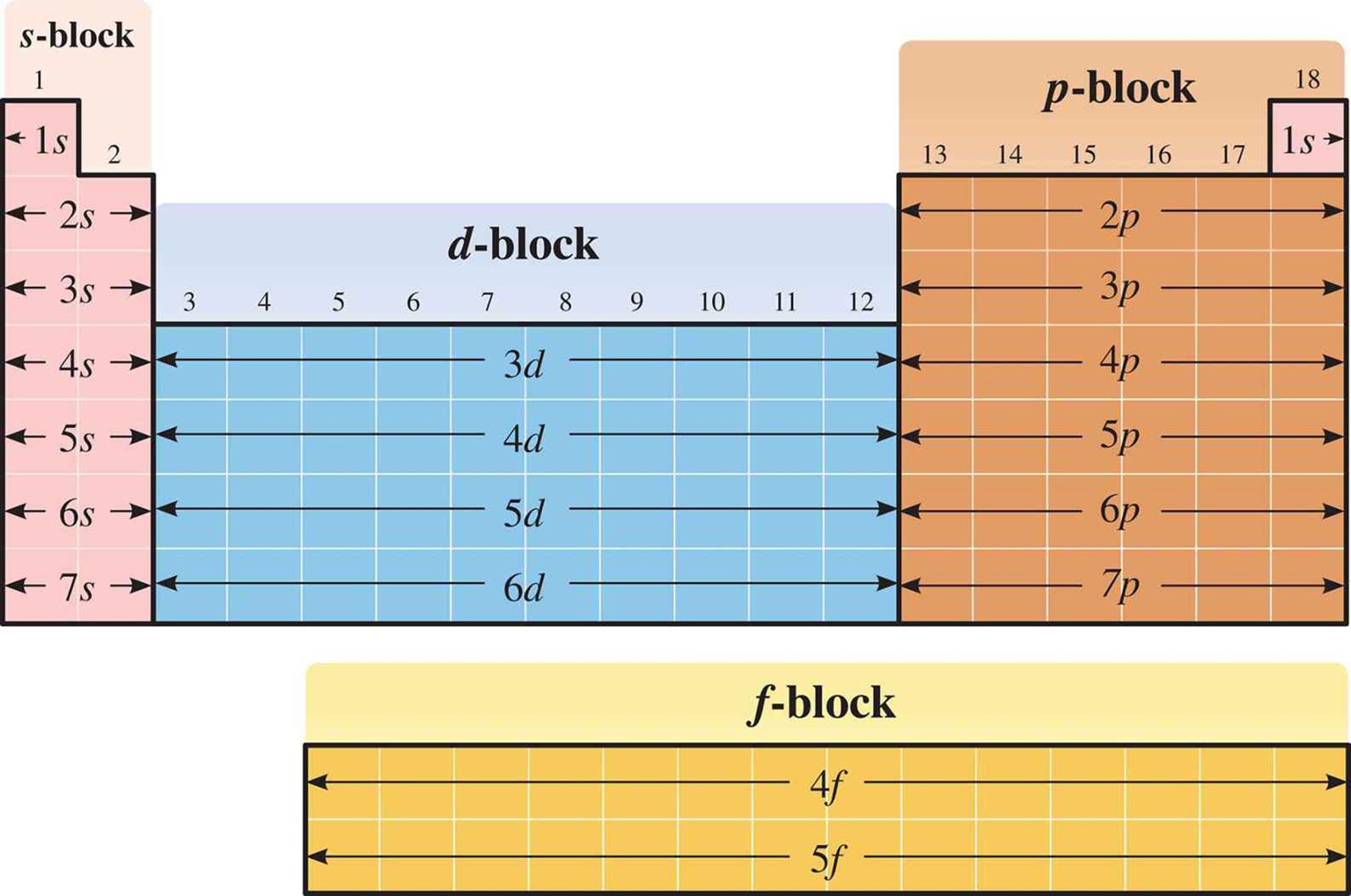 Figure 1.9. Spectroscopic Notation for Every Subshell on the Periodic Table
Figure 1.9. Spectroscopic Notation for Every Subshell on the Periodic Table
Within each subshell, there is a capacity to hold a certain number of electrons, given by:
Maximum number of electrons within a subshell = 4l + 2
Equation 1.7
where l is the azimuthal quantum number. The energies of the subshells increase with increasing l value; however, the energies of subshells from different principal energy levels may overlap. For example, the 4s subshell will have a lower energy than the 3d subshell.
Figure 1.10 provides an example of computer-generated probability maps of the first few electron clouds in a hydrogen atom. This provides a rough visual representation of the shapes of different subshells.
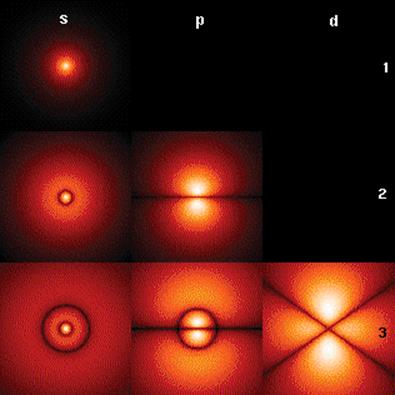 Figure 1.10. Electron Clouds of Various Subshells
Figure 1.10. Electron Clouds of Various Subshells
Magnetic Quantum Number
The third quantum number is the magnetic quantum number and is designated ml. The magnetic quantum number specifies the particular orbital within a subshell where an electron is most likely to be found at a given moment in time. Each orbital can hold a maximum of two electrons. The possible values of ml are the integers between –l and +l, including 0. For example, the s subshell, with l = 0, limits the possible ml values to 0, and because there is a single value of ml, there is only one orbital in the s subshell. The p subshell, with l = 1, limits the possible ml values to −1, 0, and +1, and because there are three values for ml, there are three orbitals in the p subshell. The d subshell has five orbitals (−2 to +2), and the f subshell has seven orbitals (−3 to +3). The shape of the orbitals, like the number of orbitals, is dependent on the subshell in which they are found. The orbitals in the s subshell are spherical, while the three orbitals in the p subshell are each dumbbell-shaped and align along the x-, y-, and z-axes. In fact, the p-orbitals are often referred to as px, py, and pz. The first five orbitals—1s, 2s, 2px, 2py, and 2pz—are demonstrated in Figure 1.11. Note the similarity to the images in Figure 1.10.
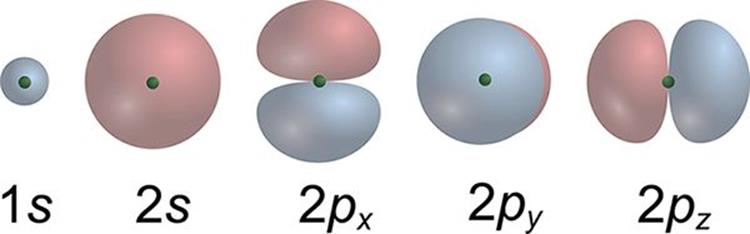 Figure 1.11. The First Five Atomic Orbitals
Figure 1.11. The First Five Atomic Orbitals
KEY CONCEPT
For any value of l, there will be 2l + 1 possible values for ml. For any n, this produces n2 orbitals. For any value of n, there will be a maximum of 2n2 electrons (two per orbital).
The shapes of the orbitals in the d and f subshells are much more complex, and the MCAT will not expect you to answer questions about their appearance. The shapes of orbitals are defined in terms of a concept called probability density, the likelihood that an electron will be found in a particular region of space.
Take a look at the 2p block in the Periodic Table. As mentioned above, 2p contains three orbitals. If each orbital can contain two electrons, then six electrons can be added during the course of filling the 2p-orbitals. As atomic number increases, so does the number of electrons (assuming the species is neutral). Therefore, it should be no surprise that the p block contains six groups of elements. The s block contains two elements in each row of the Periodic Table, the d block contains ten elements, and the f block contains fourteen elements.
Spin Quantum Number
The fourth quantum number is called the spin quantum number and is denoted by ms. In classical mechanics, an object spinning about its axis has an infinite number of possible values for its angular momentum. However, this does not apply to the electron, which has two spin orientations designated ![]() and
and ![]() Whenever two electrons are in the same orbital, they must have opposite spins. In this case, they are often referred to as being paired. Electrons in different orbitals with the same ms values are said to have parallel spins.
Whenever two electrons are in the same orbital, they must have opposite spins. In this case, they are often referred to as being paired. Electrons in different orbitals with the same ms values are said to have parallel spins.
The quantum numbers for the orbitals in the second principal energy level, with their maximum number of electrons noted in parentheses, are shown in Table 1.2.
|
n |
2 (8) |
|||
|
l |
0 (2) |
1 (6) |
||
|
ml |
0 (2) |
+1 (2) |
0 (2) |
−1(2) |
|
ms |
|
|
|
|
|
Table 1.2. Quantum Numbers for the Second Principal Energy Level |
||||
ELECTRON CONFIGURATIONS
For a given atom or ion, the pattern by which subshells are filled, as well as the number of electrons within each principal energy level and subshell, are designated by its electron configuration. Electron configurations use spectroscopic notation, wherein the first number denotes the principal energy level, the letter designates the subshell, and the superscript gives the number of electrons in that subshell. For example, 2p4 indicates that there are four electrons in the second (p) subshell of the second principal energy level. This also implies that the energy levels below 2p(that is, 1s and 2s) have already been filled, as shown in Figure 1.12.
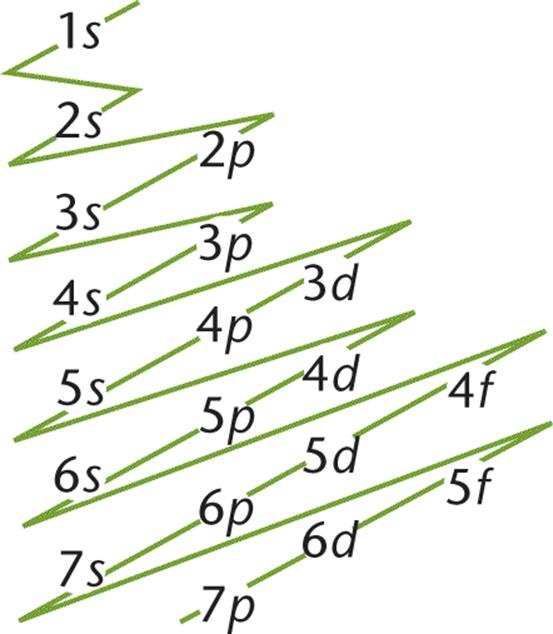 Figure 1.12. Electron Subshell Flow Diagram
Figure 1.12. Electron Subshell Flow Diagram
MCAT EXPERTISE
Remember that the shorthand used to describe the electron configuration is derived directly from the quantum numbers.
To write out an atom’s electron configuration, one needs to know the order in which subshells are filled. Electrons fill from lower- to higher-energy subshells, according to the building-up principle (also called the Aufbau principle), and each subshell will fill completely before electrons begin to enter the next one. The order need not be memorized because there are two very helpful ways of recalling this. The (n + l) rule can be used to rank subshells by increasing energy. This rule states that the lower the sum of the values of the first and second quantum numbers (n + l), the lower the energy of the subshell. This is a helpful rule to remember for Test Day. If two subshells possess the same (n + l) value, the subshell with the lower n value has a lower energy and will fill with electrons first.
Example:
Which will fill first, the 5d subshell or the 6s subshell?
Solution:
For 5d, n = 5 and l = 2, so (n + l) = 7. For 6s, n = 6 and l = 0, so (n + l) = 6. Therefore, the 6s subshell has lower energy and will fill first.
An alternative way to approach electron configurations is through simply reading the Periodic Table. One must remember that the lowest s subshell is 1s, the lowest p subshell is 2p, the lowest d subshell is 3d, and the lowest f subshell is 4f. This can be seen in Figure 1.9 earlier. Then, we can simply read across the Periodic Table to get to the element of interest, filling subshells along the way. To do this, we must know the correct position of the lanthanide and actinide series (the f block), as shown in Figure 1.13. In most representations of the Periodic Table, the f block is pulled out and placed below the rest of the Table. This is purely an effect of graphic design—placing the f block in its correct location results in a lot of excess white space on a page.
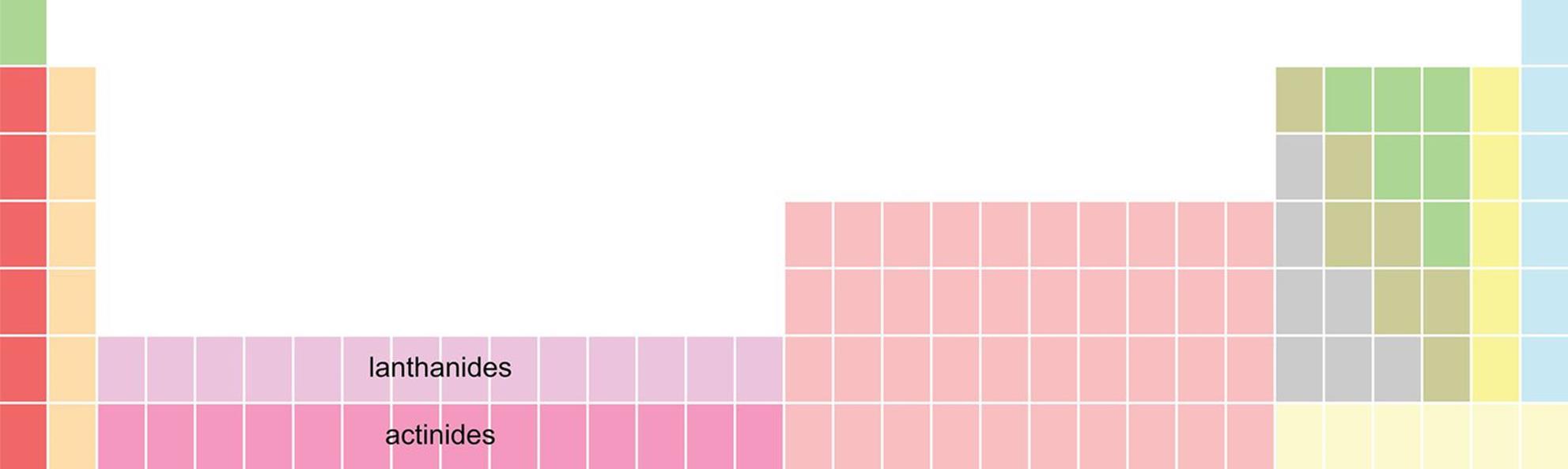 Figure 1.13. Periodic Table with Lanthanide and Actinide Series Inserted The f block fits between the s block and d block in the Periodic Table.
Figure 1.13. Periodic Table with Lanthanide and Actinide Series Inserted The f block fits between the s block and d block in the Periodic Table.
MCAT EXPERTISE
Many general chemistry courses teach the flow diagram in Figure 1.12 as a method to determine the order of subshell filling in electron configurations. However, on Test Day, it can be both time-consuming and error-prone, resulting in incorrect electron configurations. Learning to read the Periodic Table, as described here, is the best method.
Electron configurations can be abbreviated by placing the noble gas that precedes the element of interest in brackets. For example, the electron configuration of any element in period four (starting with potassium) can be abbreviated by starting with [Ar].
Example:
What is the electron configuration of osmium (Z = 76)?
Solution:
The noble gas that comes just before osmium is xenon (Z = 54). Therefore, the electron configuration can begin with [Xe]. Continuing across the Periodic Table, we pass through the 6s subshell (cesium and barium), the 4f subshell (the lanthanide series; remember its position on the Periodic Table!), and into the 5d subshell. Osmium is the sixth element in the 5d subshell, so the configuration is [Xe] 6s24f145d6
This method works for neutral atoms, but how does one write the electron configuration of an ion? Negatively charged ions (anions) have additional electrons that fill according to the same rules as above; for example, if fluorine’s electron configuration is [He] 2s22p5, then F– is [He] 2s22p6. Positively charged ions (cations) are a bit more complicated: start with the neutral atom, and remove electrons from the subshells with the highest value for n first. If multiple subshells are tied for the highest n value, then electrons are removed from the subshell with the highest l value among these.
Example:
What is the electron configuration of Fe3+?
Solution:
The electron configuration of iron is [Ar] 4s23d6. Electrons are removed from the 4s subshell before the 3d subshell because it has a higher principal quantum number. Therefore, Fe3+ has a configuration of [Ar] 3d5, not [Ar] 4s23d3.
HUND’S RULE
In subshells that contain more than one orbital, such as the 2p subshell with its three orbitals, the orbitals will fill according to Hund’s rule, which states that, within a given subshell, orbitals are filled such that there are a maximum number of half-filled orbitals with parallel spins. Like finding a seat on a crowded bus, electrons would prefer to have their own seat (orbital) before being forced to double up with another electron. Of course, the basis for this preference is electron repulsion: electrons in the same orbital tend to be closer to each other and thus repel each other more than electrons placed in different orbitals.
Example:
According to Hund’s rule, what are the orbital diagrams for nitrogen and iron?
Solution:
Nitrogen has an atomic number of 7. Thus, its electron configuration is 1s22s22p3. According to Hund’s rule, the two s-orbitals will fill completely, while the three p-orbitals will each contain one electron, all with parallel spins.
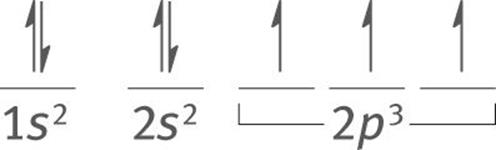
Iron has an atomic number of 26. As determined earlier, its electron configuration is [Ar] 4s23d6. The electrons will fill all of the subshells except for the 3d, which will contain four orbitals with parallel (upward) spin and one orbital with electrons of both spin directions.
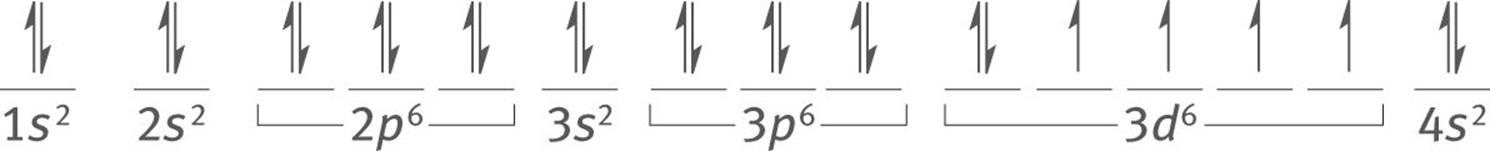
Subshells may be listed either in the order in which they fill (4s before 3d) or with subshells of the same principal quantum number grouped together, as shown here. Both methods are correct.
An important corollary from Hund’s rule is that half-filled and fully filled orbitals have lower energies (higher stability) than other states. This creates two notable exceptions to electron configuration that are often tested on the MCAT: chromium (and other elements in its group) and copper (and other elements in its group). Chromium (Z = 24) should have the electron configuration [Ar] 4s23d4 according to the rules established earlier. However, moving one electron from the 4s subshell to the 3d subshell allows the 3d subshell to be half-filled: [Ar] 4s13d5 (remember that ssubshells can hold two electrons and d subshells can hold ten). While moving the 4s electron up to the 3d-orbital is energetically unfavorable, the extra stability from making the 3d subshell half-filled outweighs that cost. Similarly, copper (Z = 29) has the electron configuration [Ar] 4s13d10, rather than [Ar] 4s23d9; a full d subshell outweighs the cost of moving an electron out of the 4s subshell. Other elements in the same group have similar behavior, moving one electron from the highest s subshell to the highest d subshell. Similar shifts can be seen with f subshells, but they arenever observed for the p subshell; the extra stability doesn’t outweigh the cost.
The presence of paired or unpaired electrons affects the chemical and magnetic properties of an atom or molecule. Materials composed of atoms with unpaired electrons will orient their spins in alignment with a magnetic field, and the material will thus be weakly attracted to the magnetic field. These materials are considered paramagnetic. An example is shown in Figure 1.14 where a ferrofluid (colloidal liquid containing a surfactant and paramagnetic particles) is influenced by the magnet beneath a glass slide. The spikes emanating from the fluid contain magnetite (an iron oxide) which is orienting along the magnetic field lines. This is similar to a typical iron filing and magnet demonstration.
 Figure 1.14. Paramagnetic Ferrofluid
Figure 1.14. Paramagnetic Ferrofluid
MNEMONIC
Remember that paramagnetic means that a magnetic field will cause parallel spins in unpaired electrons and therefore cause an attraction.
Materials consisting of atoms that have all paired electrons will be slightly repelled by a magnetic field and are said to be diamagnetic. In Figure 1.15, a piece of pyrolytic graphite is suspended in the air over strong neodymium magnets. All the electrons in this allotrope (configuration) of carbon are paired because of covalent bonding between layers of the material, and are thus opposed to being reoriented. Given sufficiently strong magnetic fields beneath an object, any diamagnetic substance can be made to levitate.
 Figure 1.15. Diamagnetic Pyrolytic Graphite
Figure 1.15. Diamagnetic Pyrolytic Graphite
REAL WORLD
The concept behind “maglev” or magnetic levitation is no longer science fiction. Using powerful magnetic fields and strongly diamagnetic materials, some transportation systems have developed frictionless, high speed rail networks such as Japan’s SCMaglev.
VALENCE ELECTRONS
The valence electrons of an atom are those electrons that are in its outermost energy shell, are most easily removed, and are available for bonding. In other words, the valence electrons are the “active” electrons of an atom and to a large extent dominate the chemical behavior of the atom. For elements in Groups IA and IIA (Groups 1 and 2), only the highest s subshell electrons are valence electrons. For elements in Groups IIIA through VIIIA (Groups 13 through 18), the highest s and p subshell electrons are valence electrons. For transition elements, the valence electrons are those in the highest s and d subshells, even though they do not have the same principal quantum number. For the lanthanide and actinide series, the valence electrons are those in the highest s and f subshells, even though they have different principal quantum numbers. All elements in period three (starting with sodium) and below may accept electrons into their d subshell, which allows them to hold more than eight electrons in their valence shell. This allows them to violate the octet rule, as discussed in Chapter 3 of MCAT General Chemistry Review.
MCAT EXPERTISE
The valence electron configuration of an atom helps us understand its properties and is ascertainable from the Periodic Table (the only “cheat sheet” available on the MCAT!). The “EXHIBIT” button on the bottom of the screen on Test Day will bring up a window with the Periodic Table. Use it as needed!
Example:
Which electrons are the valence electrons of elemental vanadium, elemental selenium, and the sulfur atom in a sulfate ion?
Solution:
Vanadium has five valence electrons: two in its 4s subshell and three in its 3d subshell.
Selenium has six valence electrons: two in its 4s subshell and four in its 4p subshell. Selenium’s 3d electrons are not part of its valence shell.
Sulfur in a sulfate ion has 12 valence electrons: its original six plus six more from the oxygens to which it is bonded. Sulfur’s 3s and 3p subshells can contain only eight of these 12 electrons; the other four electrons have entered the sulfur atom’s 3d subshell, which is normally empty in elemental sulfur.
MCAT Concept Check 1.4:
Before you move on, assess your understanding of the material with these questions.
1. If given the following quantum numbers, which element(s) do they likely refer to? (Note: Assume that these quantum numbers describe the valence electrons in the element.)
|
n |
l |
Possible Elements |
|
2 |
1 |
|
|
3 |
0 |
|
|
5 |
3 |
|
|
4 |
2 |
2. Write out and compare an orbital diagram for a neutral oxygen (O) atom and an O2– ion.
3. Magnetic resonance angiography (MRA) is a technique that can resolve defects like stenotic arteries. A contrast agent like gadolinium or manganese injected into the blood stream interacts with the strong magnetic fields of the MRI device to produce such images. Based on their orbital configurations, are these contrast agents paramagnetic or diamagnetic?
4. Determine how many valence electrons come from each subshell in the following atoms:
