Algebra Review - The Questions - 1,001 Calculus Practice Problems

1,001 Calculus Practice Problems

Part I

The Questions

In this part …

The only way to become proficient in math is through a lot of practice. Fortunately, you have now 1,001 practice opportunities right in front of you. These questions cover a variety of calculus-related concepts and range in difficulty from easy to hard. Master these problems, and you'll be well on your way to a very solid calculus foundation.

Here are the types of problems that you can expect to see:

· Algebra review (Chapter 1)

· Trigonometry review (Chapter 2)

· Limits and continuity (Chapter 3)

· Derivative fundamentals (Chapters 4 through 7)

· Applications of derivatives (Chapter 8)

· Antiderivative basics (Chapters 9 and 10)

· Applications of antiderivatives (Chapter 11)

· Antiderivatives of other common functions and L'Hôpital's rule (Chapter 12)

· More integration techniques (Chapters 13 and 14)

· Improper integrals, the trapezoid rule, and Simpson's rule (Chapter 15)

Chapter 1 Algebra Review

Performing well in calculus is impossible without a solid algebra foundation. Many calculus problems that you encounter involve a calculus concept but then require many, many steps of algebraic simplification. Having a strong algebra background will allow you to focus on the calculus concepts and not get lost in the mechanical manipulation that's required to solve the problem.

The Problems You'll Work On

In this chapter, you see a variety of algebra problems:

· Simplifying exponents and radicals

· Finding the inverse of a function

· Understanding and transforming graphs of common functions

· Finding the domain and range of a function using a graph

· Combining and simplifying polynomial expressions

What to Watch Out For

Don't let common mistakes trip you up. Some of the following suggestions may be helpful:

· Be careful when using properties of exponents. For example, when multiplying like bases, you add the exponents, and when dividing like bases, you subtract the exponents.

· Factor thoroughly in order to simplify expressions.

· Check your solutions for equations and inequalities if you're unsure of your answer. Some solutions may be extraneous!

· It's easy to forget some algebra techniques, so don't worry if you don't remember everything! Review, review, review.

Simplifying Fractions

1–13 Simplify the given fractions by adding, subtracting, multiplying, and/or dividing.

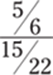
4. 9781118496718-eq01004.eps

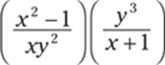
7. 9781118496718-eq01007.eps

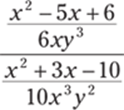
8. 9781118496718-eq01008.eps

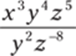
9. 9781118496718-eq01009.eps

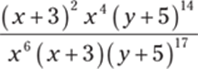
10. 9781118496718-eq01010.eps

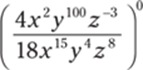
11. 9781118496718-eq01011.eps

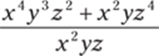
12. 9781118496718-eq01012.eps

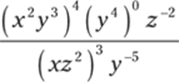
13. 9781118496718-eq01013.eps

Simplifying Radicals

14–18 Simplify the given radicals. Assume all variables are positive.

14.

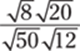
15. 9781118496718-eq01015.eps

16.

17.

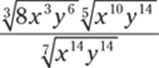
18. 9781118496718-eq01018.eps

Writing Exponents Using Radical Notation

19–20 Convert between exponential and radical notation.

19. Convert to radical notation. (Note: The final answer can have more than one radical sign.)

20. Convert to exponential notation.

The Horizontal Line Test

21–23 Use the horizontal line test to identify one-to-one functions.

21. Use the horizontal line test to determine which of the following functions is a one-to-one function and therefore has an inverse.

(A) y = x² + 4x + 6

(B)

(C)

(D) y = 3x + 8

(E)

22. Use the horizontal line test to determine which of the following functions is a one-to-one function and therefore has an inverse.

(A) y = x² – 4

(B) y = x² – 4, x ≥ 0

(D) y = x² – 4, –12 ≤ x ≤ 6

(E) y = x² – 4, –5.3 ≤ x ≤ 0.1

23. Use the horizontal line test to determine which of the following functions is a one-to-one function and therefore has an inverse.

(A) y = x⁴ + 3x² – 7

(B)

(D) y = sin x

(E) y = tan⁻¹x

Find Inverses Algebraically

24–29 Find the inverse of the one-to-one function algebraically.

24. f (x) = 4 – 5x

25. f (x) = x² – 4x, x ≥ 2

26.

27. f (x) = 3x⁵ + 7

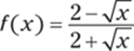
28. 9781118496718-eq01026.eps

29.

The Domain and Range of a Function and Its Inverse

30–32 Solve the given question related to a function and its inverse.

30. The set of points {(0, 1), (3, 4), (5, –6)} is on the graph of f (x), which is a one-to-one function. Which points belong to the graph of f⁻¹(x)?

31. f (x) is a one-to-one function with domain [–2, 4) and range (–1, 2). What are the domain and range of f⁻¹(x)?

32. Suppose that f (x) is a one-to-one function. What is an expression for the inverse of g(x) = f (x + c)?

Linear Equations

33–37 Solve the given linear equation.

33. 3 x + 7 = 13

34. 2 (x + 1) = 3(x + 2)

35. –4(x + 1) – 2x = 7x + 3(x – 8)

36.

37.

Quadratic Equations

38–43 Solve the quadratic equation.

38. Solve x² – 4x – 21 = 0.

39. Solve x² + 8x – 17 = 0 by completing the square.

40. Solve 2x² + 3x – 4 = 0 by completing the square.

41. Solve 6x² + 5x – 4 = 0.

42. Solve 3x² + 4x – 2 = 0.

43. Solve x¹⁰ + 7x⁵ + 10 = 0.

Solving Polynomial Equations by Factoring

44–47 Solve the polynomial equation by factoring.

44. 3 x⁴ + 2x³ – 5x² = 0

45. x⁸ + 12x⁴ + 35 = 0

46. x⁴ + 3x² – 4 = 0

47. x⁴ – 81 = 0

Absolute Value Equations

48–51 Solve the given absolute value equation.

48.

49.

50.

51.

Solving Rational Equations

52–55 Solve the given rational equation.

52.

53.

54.

55.

Polynomial and Rational Inequalities

56–59 Solve the given polynomial or rational inequality.

56. x² – 4x – 32 < 0

57. 2 x⁴ + 2x³ ≥ 12x²

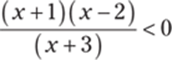
58. 9781118496718-eq01038.eps

59.

Absolute Value Inequalities

60–62 Solve the absolute value inequality.

60.

61.

62.

Graphing Common Functions

63–77 Solve the given question related to graphing common functions.

63. What is the slope of the line that goes through the points (1, 2) and (5, 9)?

64. What is the equation of the line that has a slope of 4 and goes through the point (0, 5)?

65. What is the equation of the line that goes through the points (–2, 3) and (4, 8)?

66. Find the equation of the line that goes through the point (1, 5) and is parallel to the line .

67. Find the equation of the line that goes through the point (3, –4) and is perpendicular to the line that goes through the points (3, –4) and (–6, 2).

68. What is the equation of the graph of after you stretch it vertically by a factor of 2, shift the graph 3 units to the right, and then shift it 4 units upward?

69. Find the vertex form of the parabola that passes through the point (0, 2) and has a vertex at (–2, –4).

70. Find the vertex form of the parabola that passes through the point (1, 2) and has a vertex at (–1, 6).

71. A parabola has the vertex form y = 3(x + 1)² + 4. What is the vertex form of this parabola if it's shifted 6 units to the right and 2 units down?

72. What is the equation of the graph of y = e^x after you compress the graph horizontally by a factor of 2, reflect it across the y-axis, and shift it down 5 units?

73. What is the equation of the graph of after you stretch the graph horizontally by a factor of 5, reflect it across the x-axis, and shift it up 3 units?

74. Find the equation of the third-degree polynomial that goes through the points (–4, 0), (–2, 0), (0, 3), and (1, 0).

75. Find the equation of the fourth-degree polynomial that goes through the point (1, 4) and has the roots –1, 2, and 3, where 3 is a repeated root.

76. A parabola crosses the x-axis at the points (–4, 0) and (6, 0). If the point (0, 8) is on the parabola, what is the equation of the parabola?

77. A parabola crosses the x-axis at the points (–8, 0) and (–2, 0), and the point (–4, –12) is on the parabola. What is the equation of the parabola?

Domain and Range from a Graph

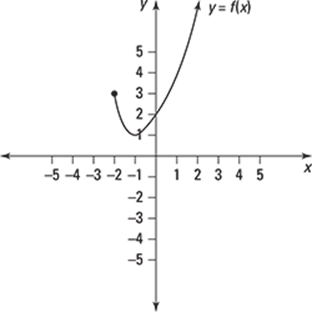
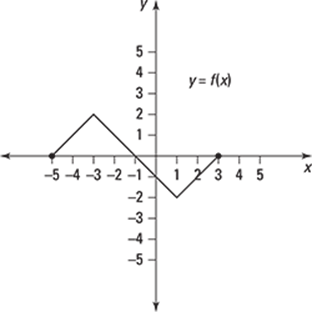
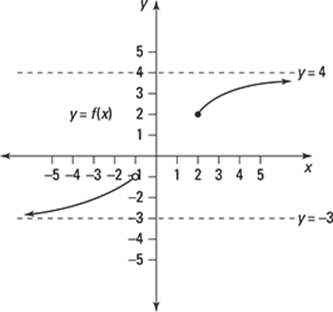
78–80 Find the domain and range of the function with the given graph.

78. 9781118496718-un0101.tif