Advanced Calculus of Several Variables (1973)

Part I. Euclidean Space and Linear Mappings

Chapter 6. DETERMINANTS

It is clear by now that a method is needed for deciding whether a given n-tuple of vectors a₁, . . . , a_n in ⁿ are linearly independent (and therefore constitute a basis for ⁿ). We discuss in this section the method of determinants. The determinant of an n × n matrix A is a real number denoted by det A or A.

The student is no doubt familiar with the definition of the determinant of a 2 × 2 or 3 × 3 matrix. If A is 2 × 2, then

For 3 × 3 matrices we have expansions by rows and columns. For example, the formula for expansion by the first row is

Formulas for expansions by rows or columns are greatly simplified by the following notation. If A is an n × n matrix, let A_ij denote the (n − 1) × (n − 1) submatrix obtained from A by deletion of the ith row and the jth column of A. Then the above formula can be written

The formula for expansion of the n × n matrix A by the ith row is

while the formula for expansion by the jth column is

For example, with n = 3 and j = 2, (2) gives

as the expansion of a 3 × 3 matrix by its second column.

One approach to the problem of defining determinants of matrices is to define the determinant of an n × n matrix by means of formulas (1) and (2), assuming inductively that determinants of (n − 1) × (n − 1) matrices have been previously defined. Of course it must be verified that expansions along different rows and/or columns give the same result. Instead of carrying through this program, we shall state without proof the basic properties of determinants (I–IV below), and then proceed to derive from them the specific facts that will be needed in subsequent chapters. For a development of the theory of determinants, including proofs of these basic properties, the student may consult the chapter on determinants in any standard linear algebra textbook.

In the statement of Property I, we are thinking of a matrix A as being a function of the column vectors of A, det A = D(A¹, . . . , Aⁿ).

(I)There exists a unique (that is, one and only one) alternating, multilinear function D, from n-tuples of vectors in ⁿ to real numbers, such that D(e₁, . . . , e_n) = 1.

The assertion that D is multilinear means that it is linear in each variable separately. That is, for each i = 1, . . . , n,

The assertion that D is alternating means that D(a₁, . . . , a_n) = 0 if a_i = a_j for some i ≠ j. In Exercises 6.1 and 6.2, we ask the student to derive from the alternating multilinearity of D that

and

Given the alternating multilinear function provided by (I), the determinant of the n × n matrix A can then be defined by

where A¹, . . . , Aⁿ are as usual the column vectors of A. Then (4) above says that the determinant of A is multiplied by r if some column of A is multiplied by r, (5) that the determinant of A is unchanged if a multiple of one column is added to another column, while (6) says that the sign of det A is changed by an interchange of any two columns of A. By virtue of the following fact, the word “column” in each of these three statements may be replaced throughout by the word “row.”

(II)The determinant of the matrix A is equal to that of its transpose A^t.

The transpose A^t of the matrix A = (a_ij) is obtained from A by interchanging the elements a_ij and a_ji, for each i and j. Another way of saying this is that the matrix A is reflected through its principal diagonal. We therefore write A^t = (a_ji) to state the fact that the element in the ith row and jth column of A^t is equal to the one in the jth row and ith column of A. For example, if

Still another way of saying this is that A^t is obtained from A by changing the rows of A to columns, and the columns to rows.

(III)The determinant of a matrix can be calculated by expansions along rows and columns, that is, by formulas (1) and (2) above.

In a systematic development, it would be proved that formulas (1) and (2) give definitions of det A that satisfy the conditions of Property I and therefore, by the uniqueness of the function D, each must agree with the definition in (7) above.

The fourth basic property of determinants is the fact that the determinant of the product of two matrices is equal to the product of their determinants.

(IV)det AB = (det A)(det B)

As an application, recall that the n × n matrix B is said to be an inverse of the n × n matrix A if and only if AB = BA = I, where I denotes the n × n identity matrix. In this case we write B = A⁻¹ (the matrix A⁻¹ is unique if it exists at all—(see Exercise 6.3), and say A is invertible. Since the fact that D(e₁, . . . , e_n) = 1 means that det I = 1, (IV) gives (det A)(det A⁻¹) = 1 ≠ 0. So a necessary condition for the existence of A⁻¹ is that det A ≠ 0. We prove in Theorem 6.3 that this condition is also sufficient. The n × n matrix A is called nonsingular if det A ≠ 0, singular if det A = 0.

We can now give the determinant criterion for the linear independence of n vectors in ⁿ.

Theorem 6.1The n vectors a₁, . . . , a_n in ⁿ are linearly independent if and only if

PROOFSuppose first that they are linearly dependent; we then want to show that D(a₁, . . . , a_n) = 0. Some one of them is then a linear combination of the others; suppose, for instance, that,

Then

because each D(a_i, a₂, . . . , a_n) = 0, i = 2, . . . , n, since D is alternating.

Conversely, suppose that the vectors a₁, . . . , a_n are linearly independent. Let A be the n × n matrix whose column vectors are a₁, . . . , a_n, and define the linear mapping L : ⁿ → ⁿ by L(x) = Ax for each (column) vector . Since L(e_i) = a_i for each i = 1, . . . , n, Im L = ⁿ and L is one-to-one by Theorem 5.1. It therefore has a linear inverse mapping L⁻¹ : ⁿ → ⁿ (Exercise 5.3); denote by B the matrix of L⁻¹. Then AB = BA = I by Theorem 4.2, so it follows from the remarks preceding the statement of the theorem that det A ≠ 0, as desired.

Determinants also have important applications to the solution of linear systems of equations. Consider the system

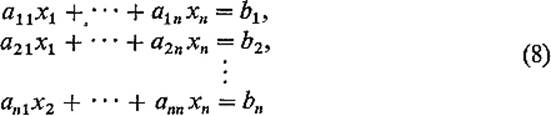
of n equations in n unknowns. In terms of the column vectors of the coefficient matrix A = (a_ij), (8) can be rewritten

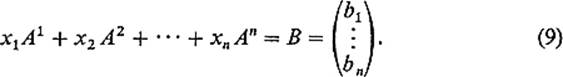
The situation then depends upon whether A is singular or nonsingular. If A is singular then, by Theorem 6.1, the vectors A¹, . . . , Aⁿ are linearly dependent, and therefore generate a proper subspace V of ⁿ. If , then (9)clearly has no solution, while if , it is easily seen that (9) infinitely many solutions (Exercise 6.5).

If the matrix A is nonsingular then, by Theorem 6.1, the vectors A¹, . . . , Aⁿ constitute a basis for ⁿ, so Eq. (9) has exactly one solution. The formula given in the following theorem, for this unique solution of (8) or (9), is known as Cramer's Rule.

Theorem 6.2Let A be a nonsingular n × n matrix and let B be a column vector. If (x₁, . . . , x_n) is the unique solution of (9), then, for each j = 1, . . . , n,

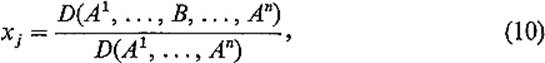
where B occurs in the jth place instead of A^j. That is,

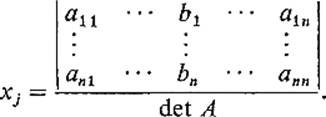
PROOFIf x₁A¹ + · · · + x_nAⁿ = B, then

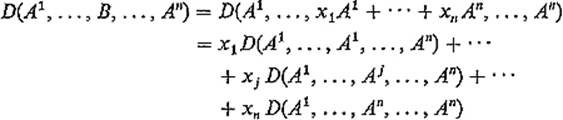
by the multilinearity of D. Then each term of this sum except the jth one vanishes by the alternating property of D, so

But, since det A ≠ 0, this is Eq. (10).

Example 1 Consider the system

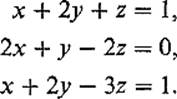
Then det A = 12 ≠ 0, so (10) gives the solution

We have noted above that an invertible n × n matrix A must be nonsingular. We now prove the converse, and give an explicit formula for A⁻¹.

Theorem 6.3Let A = (a_ij) be a nonsingular n × n matrix. Then A is invertible, with its inverse matrix B = (b_ij) given by

where the jth unit column vector occurs in the ith place.

PROOFLet X = (x_ij) denote an unknown n × n matrix. Then, from the definition of matrix products, we find that AX = I if and only if

for each j = 1, . . . , n. For each fixed j, this is a system of n linear equations in the n unknowns x_1j, . . . , x_nj, with coefficient matrix A. Since A is nonsingular, Cramer's rule gives the solution

This is the formula of the theorem, so the matrix B defined by (11) satisfies AB = I.

It remains only to prove that BA = I also. Since det A^t = det A ≠ 0, the method of the preceding paragraph gives a matrix C such that A^tC = I. Taking transposes, we obtain C^tA = I (see Exercise 6.4). Therefore

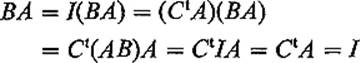
as desired.

Formula (11) can be written

Expanding the numerator along the ith column in which E^j appears, and noting the reversal of subscripts which occurs because the 1 is in the jth row and ith column, we obtain

This gives finally the formula

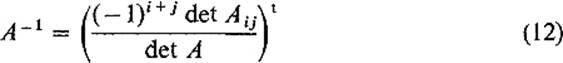
for the inverse of the nonsingular matrix A.

Exercises

6.1Deduce formulas (4) and (5) from Property I.

6.2Deduce formula (6) from Property I. Hint: Compute D(a₁, . . . , a_i + a_j, . . . , a_i + a_j, . . . , a_n), where a_i + a_j appears in both the ith place and the jth place.

6.3Prove that the inverse of an n × n matrix is unique. That is, if B and C are both inverses of the n × n matrix A, show that B = C. Hint: Look at the product CAB.

6.4If A and B are n × n matrices, show that (AB)^t = B^t A^t.

6.5If the linearly dependent vectors a₁, . . . , a_n generate the subspace V of ⁿ, and , show that b can be expressed in infinitely many ways as a linear combination of a₁, . . . , a_n.

6.6Suppose that A = (a_ij) is an n × n triangular matrix in which all elements below the principal diagonal are zero; that is, a_ij = 0 if i > j. Show that det A = a₁₁a₂₂ · · · a_nn. In particular, this is true if A is a diagonal matrix in which all elements off the principal diagonal are zero.

6.7Compute using formula (12) the inverse A⁻¹ of the coefficient matrix

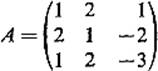
of the system of equations in Example 1. Then show that the solution

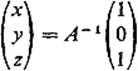
agrees with that found using Cramer's rule.

6.8Let a_i = (a_i1, a_i2, . . . , a_in), i = 1, . . . , k < n, be k linearly dependent vectors in ⁿ. Then show that every k × k submatrix of the matrix

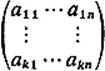
has zero determinant.

6.9If A is an n × n matrix, and x and y are (column) vectors in ⁿ, show that (Ax)·y = x·(A^ty), and then that (Ax)·(Ay) = x·(A^tAy).

6.10The n × n matrix A is said to orthogonal if and only if AA^t = I, so A is invertible with A⁻¹ = A^t. The linear transformation L: ⁿ → ⁿ is said to be orthogonal if and only if its matrix is orthogonal. Use the identity of the previous exercise to show that the linear transformation L is orthogonal if and only if it is inner product preserving (see Exercise 4.6)

6.11(a)Show that the n × n matrix A is orthogonal if and only if its column vectors are othonormal. (b) Show that the n × n matrix A is orthogonal if and only if its row vectors are orthonormal.

6.12If a₁, . . . , a_n and b₁, . . . , b_n are two different orthonormal bases for ⁿ, show that there is an orthogonal transformation L: ⁿ → ⁿ with L(a_i) = b_i for each i = 1, . . . , n. Hint: If A and B are the n × n matrices whose column vectors are a₁, . . . , a_n and b₁, . . . , b_n, respectively, why is the matrix BA⁻¹ orthogonal?