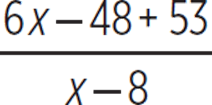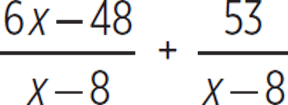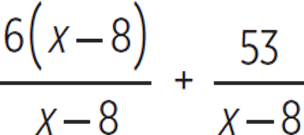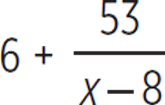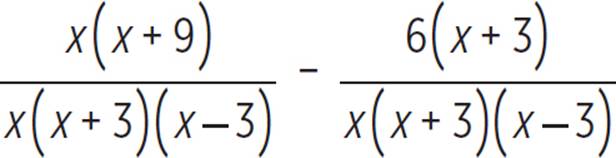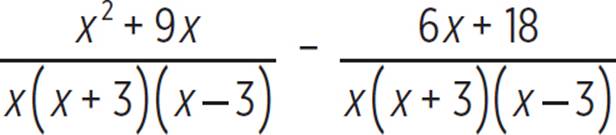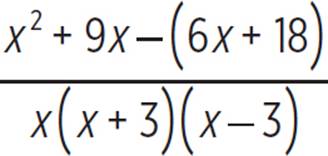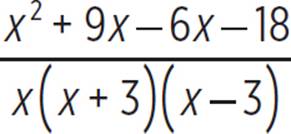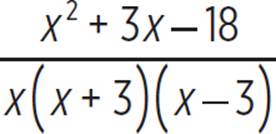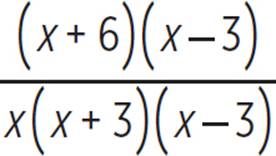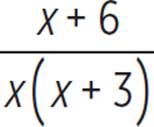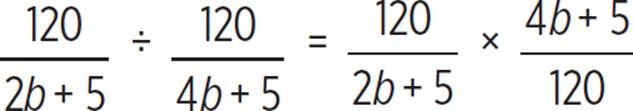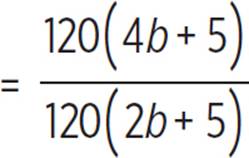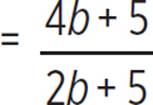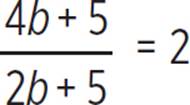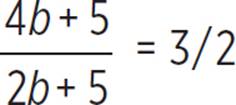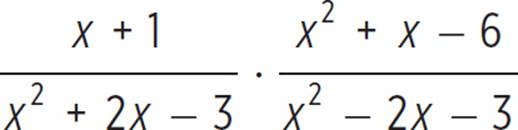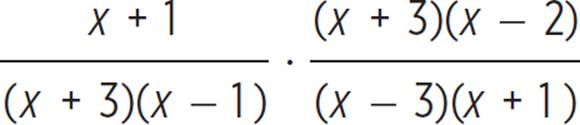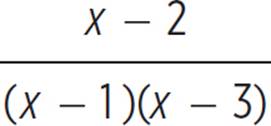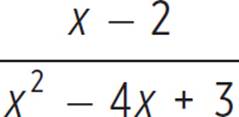High School Algebra II Unlocked (2016)

Lesson 2.4. Rational Expressions

REVIEW

RULES OF FRACTIONS:

a/1 = a

a/0 is undefined.

a/c + b/c =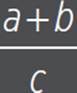

a/b ⋅ c/d = ac/bd

a/b ÷ c/d = a/b ⋅ d/c = ad/bc

ab/ac = b/c if a ≠ 0

A rational expression is an algebraic expression in the form of a ratio of two polynomials.

All those familiar rules of fractions also apply to rational expressions. For example, a ratio of the form 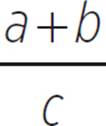can be rewritten as the sum a/c + b/c.

Keep in mind that any
polynomial is a rational
expression where the
denominator is 1.

In a direct variation, one variable is a constant multiple of the other variable, as in a = kb, where a and b are variables and k is the constant of variation. In this case, time spent setting up is equal to some constant times the square root of the number of guests, or .

An inverse variation between variables a and b is expressed in the form a = k/b. Time spent setting up is inversely proportional to the number of waiters working the event, so w must go in the denominator of the fraction set equal to time.

Only one constant of variation, c, is needed for the entire combined variation. So, the time, t, in minutes, that it takes w waiters to set up for a dinner with n guests is given by the equation t = 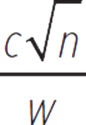. The correct answer is (E).

Rewrite the rational expression 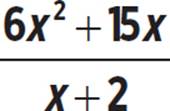as the sum of a polynomial and a rational expression.

To extract a polynomial, we need part of the numerator to be an exact multiple of the denominator. Since 6x² is 6x times x, let’s use 6x(x + 2), or 6x² + 12x.

The new expression is the sum of a polynomial (6x) and a rational expression ().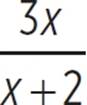

Note that x cannot equal −2, because the denominator of a fraction cannot be equal to 0.

Here is how you may see rational expressions on the SAT.

Which of the following is equivalent to the expression ?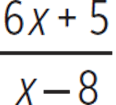

A) 6 +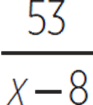

B) 6 +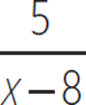

C) 6 −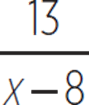

D) 6 −

A rational expression, like a numerical fraction, represents a division of the numerator by the denominator, so one way to rewrite a rational expression is to perform the long division, writing the remainder over the divisor as the remainder rational expression.

This is the same thing
we do when rewriting
an improper numerical
fraction as a mixed
number. The fraction
25/7 is the same as
25 ÷ 7, which equals 3
with a remainder of 4 over
the divisor, or 3 4/7.

Use long division to rewrite the rational expression .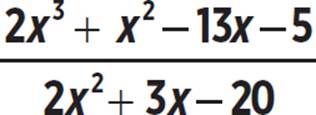

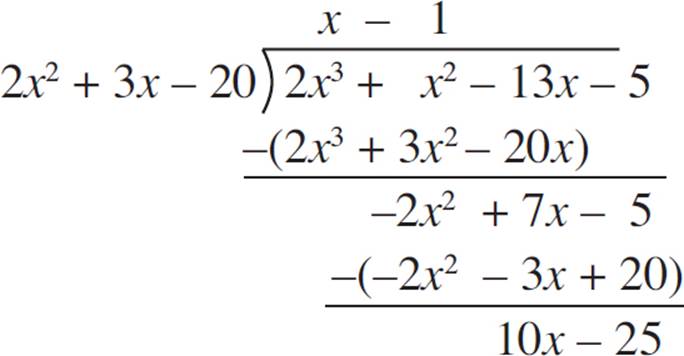
For more examples of long
division of polynomials—ones
without any remainders—see
Example 18 in Chapter 1 and
Example 4 in this chapter.

So, we can rewrite 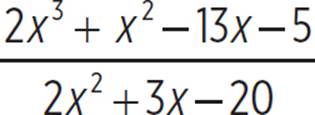as the sum of the quotient and the remainder expression: x − 1 + 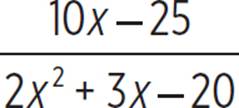. However, unless otherwise specified, we should always simplify a rational expression as much as possible.

So, 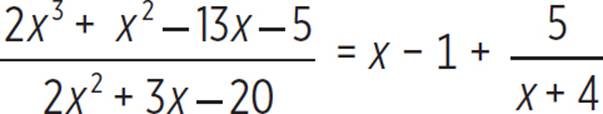, where x ≠ −4 and x ≠ 5/2.

The reason x ≠ 5/2 is because (2x − 5) was in the denominator before getting canceled out. Because 5/2 was excluded from the x-value set of the original expression, it must still be excluded from the simplified expression.

OPERATIONS WITH RATIONAL EXPRESSIONS

Like rational numbers, algebraic rational expressions are closed under addition, subtraction, multiplication, and division by a non-zero rational expression. When you perform these operations on rational expressions, the result is always a rational expression.

Use the rules of operations on rational numbers (specifically fractions) to perform operations with algebraic rational expressions. For example, to add or subtract rational expressions, find the least common denominator and convert both expressions to have that denominator.

Even when the result
of operations on
rational expressions is a
polynomial, such as 4x + 3,
this is still technically
a type of rational
expression ().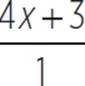

We want to rewrite the rational expression 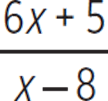as the sum of 6 and a leftover rational expression. To do this, we need to break the given rational expression into a sum of two rational expressions, one of which is equal to 6. The denominator is x − 8, so a rational expression equal to 6 and having this denominator is 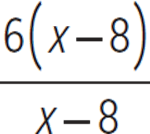, or 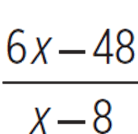. We need to include 6x − 48 in the numerator but keep the total value of 6x + 5. In other words, we must rewrite the numerator 6x + 5 as 6x − 48 + 53. (Adding 53 to −48 produces 5.)

Alternatively, we could use long division to rewrite the given rational expression.

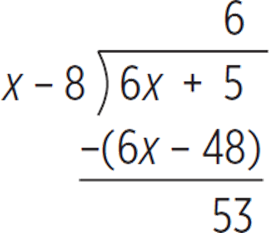
So, (6x + 5) divided by (x − 8) is equal to 6 with a remainder of 53, or 6 + 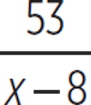. The correct answer is (A).

Subtract: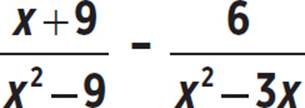

First, let’s factor each denominator, so that we can identify any common factors.

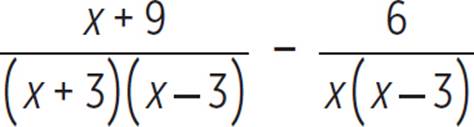
The denominators share a common factor of (x − 3). The least common multiple of x² − 9 and x² − 3x is x(x + 3)(x − 3), so the least common denominator is x(x + 3)(x − 3). To convert the first term to have that denominator, we must multiply its numerator and its denominator by x. To convert the second term, we must multiply its numerator and its denominator by (x + 3).

The difference is 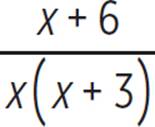, or 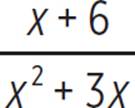, with x ≠ 3, x ≠ 0, and x ≠ −3.

To multiply two rational expressions, multiply the numerators and multiply the denominators. To divide one rational expression by another, multiply the dividend expression by the reciprocal of the divisor expression. In either situation, remember to then simplify by cancelling out any common factors in the numerator and denominator of the product.

Paula, Peyton, and Phaedra pick apples at an orchard. Paula picks at a rate of b bushels per hour. Peyton picks 5 more bushels per hour than Paula. Phaedra picks twice as many bushels per hour as Paula. Yesterday all three of them picked apples. Today only Paula and Peyton are picking apples. How many times as long will it take just Paula and Peyton to pick 120 bushels as it would for Paula, Peyton, and Phaedra working together? Express your answer as a rational expression in terms of b. At what apple-picking rate of Paula’s would it take twice as long for Paula and Peyton to pick 120 bushels as all three pickers working together? At what rate of Paula’s would it take 1 1/2 times as long for Paula and Peyton to pick 120 bushels as all three pickers working together?

b = Paula’s rate, in bushels per hour

b + 5 = Peyton’s rate, in bushels per hour

2b = Phaedra’s rate, in bushels per hour

The time it takes to pick 120 bushels is the total number of bushels (120) divided by the rate, in bushels per hour. The rate for Paula and Peyton working together is b + b + 5, or 2b + 5. So, the time it takes Paula and Peyton to pick 120 bushels together is .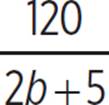

This is a variation on the
d = rt, or t = d/r, formula.
In this case, the “distance”
is instead total number
of apples picked.

The rate for all three people working together is b + b + 5 + 2b, or 4b + 5. The time it takes Paula, Peyton, and Phaedra to pick 120 bushels is .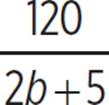

To find how many times as long it will take just Paula and Peyton to pick 120 bushels as Paula, Peyton, and Phaedra, we must divide the time for just Paula and Peyton by the time for all three pickers.

To find out at what apple-picking rate of Paula’s it would take twice as long for just the two pickers to pick 120 bushels, as compared to all three pickers working together, we must find the b-value that makes the ratio of times equal to 2.

This equation is not true, so there is no rate b such that it will take just Paula and Peyton twice as long as all three of them.

Find at what rate of Paula’s (what value of b) it will take 1 1/2 times as long for Paula and Peyton to pick 120 bushels as it would take all three pickers working together.

If Paula picks apples at a rate of 2.5 bushels per hour, then it will take Paula and Peyton 1 1/2 times as long to pick 120 bushels as Paula, Peyton, and Phaedra all working together.

DRILL

CHAPTER 2 PRACTICE QUESTIONS

Click here to download a PDF of Chapter 2 Practice Questions.

Directions: Complete the following open-ended problems as specified by each question stem. For extra practice after answering each question, try using an alternative method to solve the problem or check your work.

1. The variable b varies inversely as a, and b = 13.5 when a = 4.5. Find the constant of variation, write an equation for the relationship, and find b when a is 0.5.

2. Write an equation for the volume of a rectangular prism with a length of l inches, a width of w inches, and a height of 8 inches. Identify the type of variation and the constant of variation, then find the volume of the prism if the length of the base is 4 inches and the width of the base is 2 inches.

3. What are the roots of the polynomial 2x³ + 26ix² − 44x?

4. Simplify .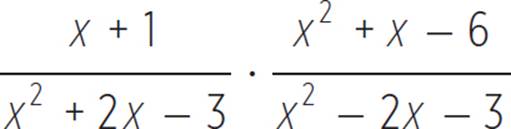

5. How many roots does x³ − 5x² + 144x − 720 have? What are the roots?

6. Solve the equation x⁵ − x⁴ = 2x³ + 4x² + 24x.

7. Simplify the expression .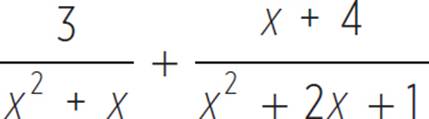

8. The monthly payment, m, on a mortgage varies directly with the amount borrowed, A. If the monthly payment on a 30-year mortgage is $7.82 for every $2,000 borrowed, find a formula that relates the monthly payment to the amount borrowed for a mortgage with these terms. Then find the monthly payment when the amount borrowed is $120,000.

9. A box has a volume given by 2x³ − 3x² − 39x + 20. If the height of the box is given by 2x − 1, what is the area of the base? If the length is given by x + 2, find a sum of a polynomial and a rational expression that would be equivalent to the width.

SOLUTIONS TO CHAPTER 2 PRACTICE QUESTIONS

1. constant of variation: 60.75; equation: ab = 60.75; b = 121.5

Start with the expression for inverse variation: ab = k and make the appropriate substitutions to evaluate the constant of variation.

ab = k

(4.5)(13.5) = k

k = 60.75

Thus, an equation for the relationship is ab = 60.75. Since we now must solve for b, it can be helpful to rewrite the equation as b = 60.75/a. Plug in a = 0.5 and evaluate for b.

b = 60.75/a

b = 60.75/(0.5)

b = 121.5

2. 64

The volume of a rectangular prism is V = lwh.

V = lwh

V = lw(8), or 8lw

Thus, volume varies jointly with the length, l, and width, w. The constant of variation is 8.

Next, use the provided dimensions to calculate the volume of the prism. V = 8lw = 8(4)(2) = 64

The volume is 64 cubic inches.

3. 0, −11i, and −2i

Since this polynomial is a cubic function (degree 3), it will have three total roots. First, factor out the common term of 2x; this will give (2x)(x² + 13ix − 22). Since there is an i term in the coefficient, rewrite −22 in terms of i; this gives the form (2x)[x² + 13ix + (−22)], or (2x)[x² + 13ix + (22i²)]. This can be factored into the form (2x)(x + 11i)(x + 2i), giving the three roots of 0, −11i, and −2i.

4.

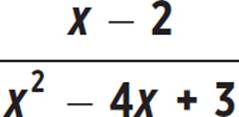
Begin by factoring the numerators and denominators to cancel out common factors.

5. 3 roots; 5, 12i, and −12i

Since the expression has a degree of 3, the expression has 3 roots. At first, this expression does not look easy to factor; however, by grouping the first two terms and the second two terms, they can be factored.

x³ − 5x² + 144x − 720 = 0

(x³ − 5x²) + (144x − 720) = 0

x²(x − 5) + 144(x − 5) = 0

(x² + 144)(x − 5) = 0

x² + 144 = 0 x − 5 = 0

x² = −144 x = 5

x = ±12i

So, the solutions are 5, 12i, and −12i.

6. −2, 0, 3, 2i, and −2i

This can be rewritten as a system of equations by setting each side of the equation equal to y, as shown here:

y = x⁵ − x⁴

y = 2x³ + 4x² + 24x

Any x-value that produces the same y-value in each equation would be a solution; therefore, graph the equations. The graph would look something like the following:

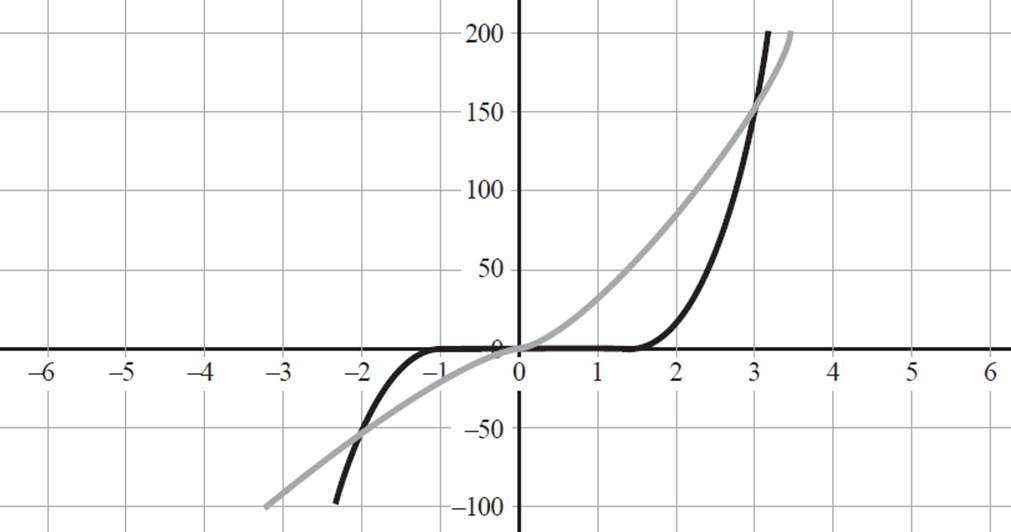
There appear to be three solutions shown, at x-values of −2, 0, and 3. If tested in the original equation, these would indeed work; an x-value of −2 would give −48 = −48, a y-value of 0 would give 0 for both, and an x-value of 3 would give 162 for both. Therefore, those are three solutions.

However, the highest exponent shown is 5, so there should be a total of 5 solutions. Start by moving everything over to one side of the equation: x⁵ − x⁴ − 2x³ − 4x² − 24x = 0

The three roots found go with factors of x, (x + 2), and (x − 3); multiply those together. x(x + 2)(x − 3) = (x² + 2x)(x − 3)= x³ − 3x² + 2x² − 6x = x³ − x² − 6x

Divide this into the original equation to find what is left over:

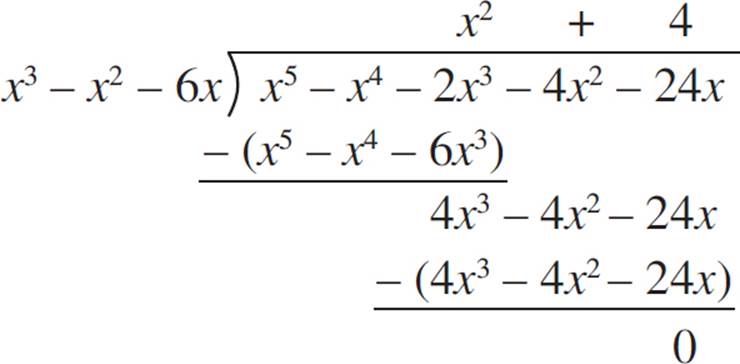
The final factor is (x² + 4), which has roots 2i and −2i. Therefore, the five solutions to the system of equations are −2, 0, 3, 2i, and −2i.

7.

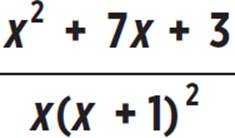
First, factor the denominators to determine the Lowest Common Denominator so it will be possible to add the numerators. The first denominator, x² + x, factors to x(x + 1), and the second denominator, x² + 2x + 1, factors to (x + 1)². Therefore, the least common denominator possible here is x(x + 1)². Multiply the first fraction by 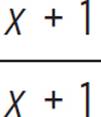and the second fraction by so both rational expressions will have the same denominator. This will give 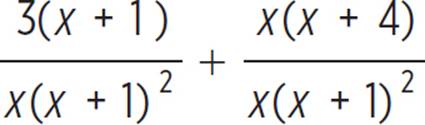. Since the denominators are now the same, the numerators can be added above the common denominator; this gives 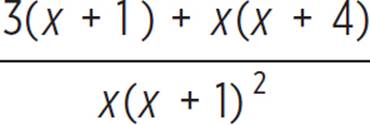. Given there are products to be found in the numerator, distribute to simplify; the result is 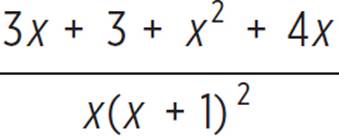. Finally, combine like terms to get the final answer of 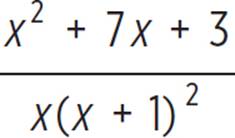. Since this final numerator does not factor there is no more simplification that can be done here, so the final answer is .

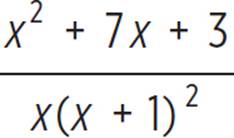8. $469.20

Because m varies directly with A, we know that m = kA. Use the given values to determine the constant of variation.

m = kA

7.82 = k(2000)

k = 0.00391

Thus, the formula is m = 0.00391A. Next, use this to determine m when A = 120,000.

m = 0.00391A

m = 0.00391(120,000)

m = 469.2

So, when the amount borrowed is $120,000, the monthly payment would be $469.20.

9. x − 3 −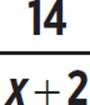

Since volume of a box is given by lwh and the area of the base of a box is given by lw, this can be set up as 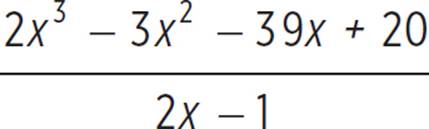. To find the area of the base, complete the division:

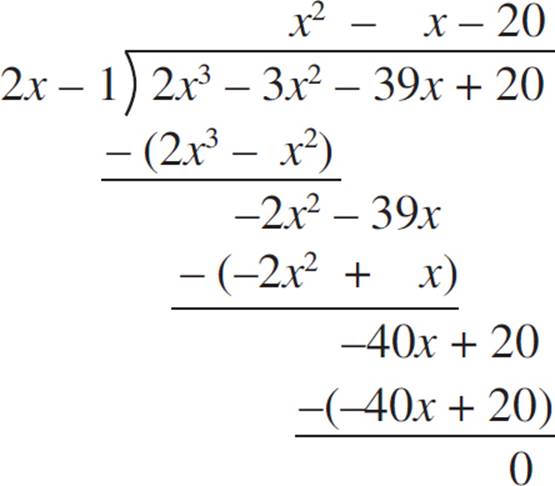
This gives the area of the base as x² − x − 20. However, as the question also wants the width of the box, this quadratic needs to be further broken down. To find the width, you must divide the quadratic by the length, which is x + 2. Write this as a rational expression: 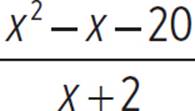. To extract a polynomial term, this needs to be rewritten in a form to allow us to extract something; for example, rewrite the numerator as x² + 2x − 3x − 20. This would allow the expression to be broken down as 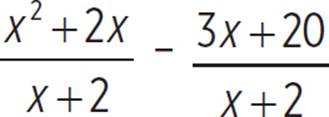. The first term would be factored as 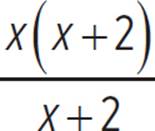, which is just x. The second piece can further be broken down by rewriting 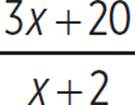as 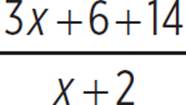; this would break into 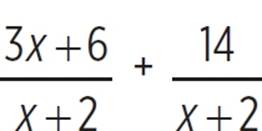, or .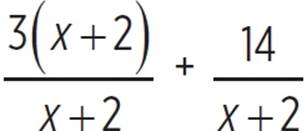

The x + 2 terms cancel in the first piece here, leaving just 3 + 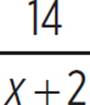. Putting everything together, this gives the expression x − (3 + 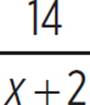), which simplifies as x − 3 − .

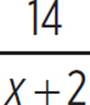REFLECT

Congratulations on completing Chapter 2!
Here’s what we just covered.
Rate your confidence in your ability to:

• Determine how many roots a polynomial has, based on the degree of the polynomial

1 2 3 4 5

• Factor polynomials with imaginary number coefficients

1 2 3 4 5

• Create and solve systems of equations to solve single-variable polynomial equations

1 2 3 4 5

• Identify and apply direct, inverse, joint, and combined variations

1 2 3 4 5

• Perform arithmetic operations with rational expressions

1 2 3 4 5

• Rewrite rational expressions as the sum of a polynomial and a remainder expression

1 2 3 4 5

If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.

Access your online student tools for a handy, printable list of Key Points for this chapter. These can be helpful for retaining what you’ve learned as you continue to explore these topics.