Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 3. Limits and Continuity
SPECIAL LIMITS
You have a number of techniques available to you now to evaluate limits and to interpret the continuity that is dependent on those limits. Before you are completely proficient at limits, however, there are four limits you need to be able to recognize on sight. (BC students have still another topic to cover concerning limits—L’Hopital’s Rule—but that occurs in Chapter 5.) I call these “special” limits because we accept them without formal proof and because of the special way they make you feel all tingly inside.
Four Special Limits
1. 
if c is a nonzero constant and n is a positive integer
Justification: In the simplest case (c = 1, n =1), you are considering 
You should know the graph of 1/x by heart, and its height clearly approaches zero as x approaches infinity. The same will happen with any c value. Remember that the denominator is approaching infinity, so it is getting very large, while the numerator is remaining fixed. The denominator will eventually get so large, in fact, that no matter how large the numerator is, the fraction has an extremely small value so close to zero that the difference is negligible. This limit rule works the same way for other eligible n values. Consider 
The denominator is growing larger more quickly than in the previous example, while 7 remains constant. Clearly, this limit is also equal to 0.
2. 
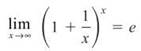
Justification: Using the first special limit rule, 
Technically, 
is a number very close to, but not quite, one. That small difference becomes magnified when raised to the x power, and the result is e. To visually verify that the limit is accurate, use your graphing calculator to calculate 
for a very large value of x. For example, if x = 100,000,000, 
which is approximately the value of e, accurate to seven decimal places.
3. 
Justification: This is easily proven by L’Hopital’s Rule, but that is outside the spectrum of Calculus AB, so ABers will have to satisfy themselves with the graph of 
as proof.
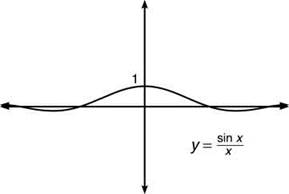
Note that the formula above uses a instead of x, because the rule holds true for more than just 
For example, you can set a = 5x3 and the formula still works: 
4. 
Justification: Again, L’Hopital’s Rule makes this easy, but the graph will suffice as proof; also, any value of a will make this true.
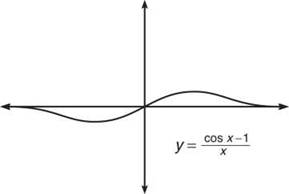
Example 11: Evaluate each of the following limits.
(a) 
You can do each of these limits separately and add the results:
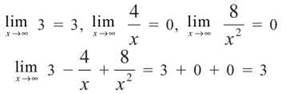
The last two limits are possible because of Special Limit Rule 1.
b)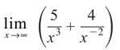 
You can rewrite this as
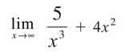
Although 5/x3 has a limit of 0 as x approaches infinity, 4x2 will grow infinitely large. The resulting sum will have no limiting value, so the limit is 0 + ∞ = ∞. (No limit exists.)
c) 
This is not quite the form of Special Limit Rule 3—the 3x and x have to match. However, if you multiply the fraction by 3/3, you get
Now, Special Limit Rule 3 applies:
Notice that 3 ∙ 1 is not affected by the limit statement at all in the last step; the x may be approaching 0, but there are no x’s left in the problem!
NOTE. You are allowed to multiply by 3/3 in Example 11(c) because doing so is the same as multiplying by 1—you are not changing the value of the fraction.
d)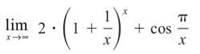 
By Special Limit Rule 2, 
Note that π/x will follow Special Limit Rule 1, since π is a constant. Therefore, you get:
Therefore, the solution is 2e + 1.
Example 11 demonstrates that the presence of addition and subtraction does not affect the outcome of the limit. Each piece of the limit can be done separately and combined at the end.
EXERCISE 7
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
DO NOT USE A GRAPHING CALCULATOR FOR ANY OF THESE PROBLEMS.
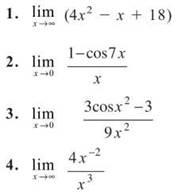
ANSWERS AND EXPLANATIONS
1. 
Some texts propose very complicated means to prove this. However, the question is very easy if you consider the graph of y = 4x2 — x + 18—it is a parabola facing upward. Therefore, It is also correct to say that no limit exists because the function increases without bound.
2. This is almost of the form 
Multiply the numerator and denominator by 7, and factor out a negative to make it match that form:
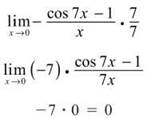
3. Again, some minor massaging is necessary to use Special Limit Rule 4:
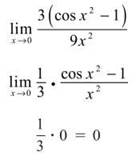
4. This fraction can be rewritten to give you 
. According to Special Limit Rule 1, this is of form c/xn, so the limit is 0.