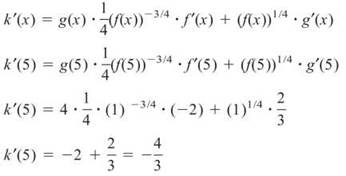Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 4. Differentiating
THE PRODUCT RULE
If asked to find the derivative of f(x) = sin x + cos x, you should have no trouble by now. You wouldn’t need to furrow your brow and scratch your chin like a gorilla trying to determine how to file its federal tax return. You’d know that f is the sum of two functions, so the derivative is simply the sum of the individual funtions’ derivatives:
f'(x) = cos x — sin x
Given the function g(x) = sin x cos x, you might be tempted to use the same strategy and give the derivative g'(x) = (cos x)(—sin x), but this is not correct. Any time you want to find the derivative of a product of two non-constant functions, you must apply the Product Rule:
The Product Rule: If h(x) = f(x)g(x), then h'(x) = f(x)g'(x) + g(x)f'(x).
Translation: To find the derivative of a product, differentiate one of the factors and multiply by the other; then, reverse the process, and add the two results together.
For example, in order to differentiate g(x) = sin x cos x, you multiply sin x by the derivative of cos x and add to that cos x times the derivative of sin x:
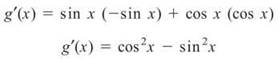
g'(x) = cos 2x (by a double angle formula)
NOTE. To find the derivatives of ln x2, arctan 2x, and e4x2 in Examples 10 and 11, you need to apply the Chain Rule.
Example 10: Find dy/dx if y = cos x ln x
Solution: Because you are given a product of two functions, apply the Product Rule. I have denoted which derivatives to take below with a prime symbol ('). It’s not wonderful notation, but it gets the point across:
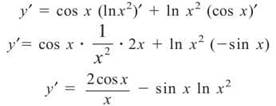
Example 11: Find dy/dx using the Product Rule if ![]()
Solution: You can rewrite the expression as the product
![]()
and apply the Product Rule as follows:
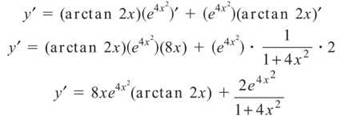
EXERCISE 5
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
DO NOT USE A GRAPHING CALCULATOR FOR ANY OF THESE PROBLEMS.
1. Why don’t you have to use the Product Rule to find the derivative of y = 7x?
2. Find dy/dx if ![]()
3. Find dp/dx if p = sec x ∙ arcsec x
4. Find d/dx ![]()
5. Evaluate y'(x) if y = sin x cos x tan x
6. Evaluate h'(2) if h(x) = 2x ∙ log2x
7. Given functions f and g such that f(5) = 1, f'(5) = —2, g(5) = 4, and g'(5) = 2/3, if ![]() evaluate k'(5).
evaluate k'(5).
ANSWERS AND EXPLANATIONS
1. The Product Rule must be applied when deriving the product of non-constant functions. 7 is a constant. However, the Product Rule will work when finding d/dx(7x)—try it! Remember that the derivative of 7 is 0 since 7 is a constant.
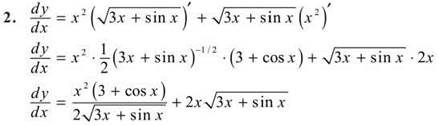
3. These functions are inverses, not reciprocals, so their product is not 1.
![]()
4. If you wish, you can expand each of the polynomials and multiply them together; only the Power Rule will be necessary, but you’ll be multiplying all day long. Best to use the Power, Chain, and Product Rules all combined:
![]()
You can rewrite the expression to make it slightly more pretty, but that is not necessary.
5. You can generalize the Product Rule to any number of factors. The key is to take only one derivative at a time, leaving the other factors alone.
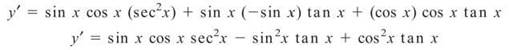
6. To find h'(2), find h’(x) and substitute 2 for x.
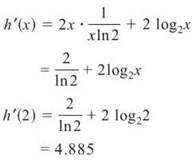
NOTE. On the AP test, either you will be told what variable to differentiate with respect to, or it will be obvious.
7. The function can be rewritten as
![]()
and now the Product Rule can be applied.