Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 7. Integration

OVERVIEW

• Basic antiderivatives

• Hands-On Activity 7.1: Approximating area with Riemann sums

• The trapezoidal rule

• The fundamental theorem of calculus

• Hands-On Activity 7.2: Accumulation functions

• The Mean Value Theorem for Integration, average value of a function

• U-Substitution

• Integrating inverse trigonometric functions

• Technology: Evaluating definite integrals with your graphing calculator

• Summing it up

Now that you know just about everything there is to know about taking derivatives, it’s time to pull the rug out from under you. The third major topic of calculus (limits and derivatives being the first two) is integration, or antidifferentiation. That’s right, Mr. Prefix; anti- means “the opposite of,” so it’s time to explore the process of derivatives reversed. Previously, you would be asked to find clearly, the answer is 3x². Now, you’ll be given 3x² and required to come up with the antiderivative, x³.

But, it’s never that easy, is it? As a matter of fact, x³ + 1 is also an antiderivative of 3x²! So is x³ — 14. Therefore, we say that the antiderivative of 3x² is x³ + C, where C can be any number at all. But, we’re getting ahead of ourselves. Let’s jump right in—the water’s fine.

BASIC ANTIDERIVATIVES

Just as the notation dy/dx or y’ indicated to you that differentiation was necessary, the notation

indicates the same for integration. The above is read “the integral (or antiderivative) of f(x) with respect to x.” Respecting variables in differentiation was sometimes a complicated procedure. Remember implicit differentiation and related rates? Luckily, respecting variables is not nearly as difficult in integration; you just have to make sure the dx gets multiplied by everything in the integral. But, enough talk—let’s get down to business.

NOTE. When deriving x^b, you multiplied by b and subtracted 1 from the power. When integrating x^b, you add 1 to the power and divide. The processes are complete opposites of each other.

Think back for a moment: The Power Rule (one of your earliest and dearest calculus friends) dealt with deriving simple expressions—a single variable to a constant power. There is an equivalent rule for integrating, so we’ll call it (get this) the Power Rule for Integration. Clever, eh?

The Power Rule for Integration: If a is a constant,

Translation: In order to find the integral of x^a, add 1 to the exponent and divide the term by the new exponent.

Example 1: Evaluate

Solution: Add one to the exponent (1 + 3 = 4), and divide by the new exponent, 4:

NOTE. It is not always impossible to find C. In fact, it is sometimes incorrect to write “+ C”. For now, however, make it a habit to automatically add the “+ C” when you integrate. You’ll learn more about the exceptions later.

More about that weird C now. It is called the constant of integration. It is simply a real number, and we have no idea exactly what that number is (for now). However, and all have a derivative of x³ (since the derivative of the constant is 0). Therefore, when we write “+ C” at the end of an antiderivative, we are admitting that there may have been a constant there, but we do not know it.

Now, let’s discuss the two major properties of integrals; both of them are very similar to derivatives:

If a constant or coefficient is present in your integral, you may ignore it, like you did with derivatives. In fact, you may pull the constant completely out of the integral.

If an integral contains numerous terms being added or subtracted, then these terms can be split apart into separate integrals. In differentiation, given the problem you could find the derivatives of the terms separately: 3x² — 5. The same goes for integration. For example,

In Example 2, we’ll apply these properties of integration to some more complex integration problems.

ALERT! You can only pull coefficients out of integrals. For example, it would be incorrect to rewrite

Example 2: Evaluate the following antiderivatives:

This expression can be rewritten as

The 5/3 is merely a coefficient, so we can apply the first rule of antiderivatives and pull it out of the integral:

Now, apply the power rule for integrals, but make sure to add 1 to the original power of -2.

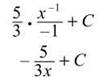
This integral must first be rewritten as

Because the two terms are being added, we can split the above into two separate integrals (and pull out the coefficients):

Now, apply the Power Rule for Integration:

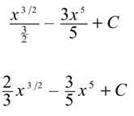
The 3/2 power is the result of adding 1 to the original exponent (1/2).

ALERT! Once you integrate, make sure to stop writing the and dx symbols. They only hang around until you’re done integrating. When their work is done, they vanish.

Again, rewriting the integral is the first order of business. Instead of one fraction, rewrite as the sum of two fractions with the same denominator. Also, apply the integration properties:

Remember way back to algebra and exponent properties: 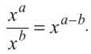Therefore, and Use this to rewrite the problem as

and apply the Power Rule for Integrals to get

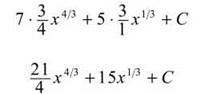
Do you see the shortcut for integrating fractional exponents? When you integrate x^1/3, instead of writing the step remember that dividing by 4/3 is the same as multiplying by 3/4. Therefore, the answer is

Well, the Power Rule for Integrals is all well and good, but there is one instance in which it is completely useless. Consider the integral:

ALERT! Although the Power Rule for Integrals is relatively easy, it is also easy to make mistakes when the exponents are fractions or have negative powers. Be careful.

This can be rewritten as but if you try to integrate, you get and the zero in the denominator spoils everything. How, then, are you to integrate 1/x? Believe it or not, you already know the answer to this—you just have to dig it out of your long-term memory. Remember, integration is the opposite of differentiation, so the expression that has the derivative of 1/x will be the integral of 1/x. You learned in Chapter 4 that Therefore,

(You need to use the absolute value signs since ln x has domain (0,∞)—the function wouldn’t know what to do with negative inputs.) If you have forgotten the large list of derivatives you were to have memorized, it’s time to refresh your memory. Only two of the integrals look a little different from their derivatives. We have already looked at the first: (its integral has that unexpected absolute value). One other problem shows a slight difference in its absolute values:

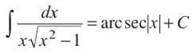
You see arcsec x so infrequently on the test, it’s hardly worth mentioning, but it is important. In addition, we will take a closer look at inverse trigonometric and exponential integrals a little later in this chapter. Here are a few problems to get you brushed up on the throwback integrals.

Example 3: Evaluate the following integrals:

This problem asks, “What has a derivative of —sin x?” The answer is, of course, cos x + C, since If the problem had been the answer would have been —cos x + C, since

First, rewrite this problem as What has a derivative of csc² x? Well, and that’s only off by a negative sign. Therefore, add a negative sign to cot x to account for the missing sign, and the answer is

This is simply the derivative of arcsin x, so the answer is arcsin x + C.

If the derivative of e^x is e^x, then

NOTE. You need to learn a technique called u-substitution before we can get too hot and heavy into integration. That’s later, though.

TIP. If you’re not sure that your integral is correct, take its derivative to check and see if you get the original problem. Because integration and differentiation are inverses, they should cancel each other out.

EXERCISE 1

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

DO NOT USE A GRAPHING CALCULATOR FOR ANY OF THESE PROBLEMS

Evaluate each of the following integrals.

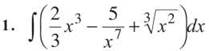
if a and b are real numbers

ANSWERS AND EXPLANATIONS

1. Begin by splitting the integral into pieces and rewriting it so that you can apply the Power Rule for Integrals:

It’s ready to be power ruled, so go to it:

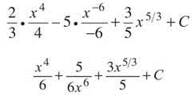
2. Because b is a coefficient, it can be pulled out of the integral.

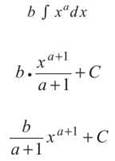
3. Rewrite this integral before starting, and remember that 2π is just a constant, so the Power Rule for Integrals still applies (just like it did to the a exponent in problem 2).

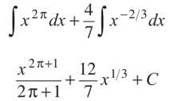
4. Before you can integrate, you need to multiply the binomials together. There is no Product Rule for Integration (which makes things tricky later) but for now, we can avoid the problem by multiplying.

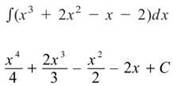
5. You can begin by writing each of the terms of the numerator over the denominator. This is a long step, and if you can do it in your head, you are encouraged to do so—carefully! So that you can see exactly what’s happening, the step is included:

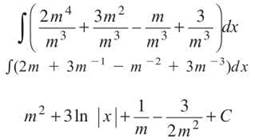
6. This problem looks pretty complicated, but if you are clever (and who doesn’t like being clever now and again?), it becomes quite easy. The trick is to rewrite the fraction as follows:

If you multiply those two fractions together, you still get so we haven’t actually changed anything’s value. However, now we can rewrite as tan x and as sec x:

Perhaps you’ll remember it better if it’s written this way:

You know that is the derivative of sec x, so the final answer is

sec x + C

7. That negative sign looks like it’s just beggin’ to get factored out, so we’ll oblige it (and bring it out of the integral as the coefficient —1):

Now that looks familiar. In fact, it is most of the Pappa Theorem! (Remember your Pappa: tan² x + 1 = sec² x.) Therefore, we’ll use a Pappa substitution to rewrite it:

Because tan x has a derivative of sec²x, the answer is

—tan x + C

8. Even though this looks ugly, begin the same way you did with problem 5—write each term of the numerator over the denominator:

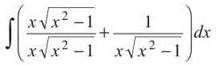
The first gigantic fraction simplifies to 1, making things much, much happier in the world:

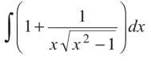
The integral of 1 is simply x (since ), and the other term is the derivative of arcsec x (don’t forget the absolute value signs we discussed earlier in this section):

x + arcsec |x| + C