Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 8. Advanced Methods of Integration
IMPROPER INTEGRALS (BC TOPIC ONLY)
Improper integrals are bizarre integrals that have at least one of the three following qualities: (1) one of the limits of integration is infinity, (2) the curve being integrated has an infinite discontinuity between the limits of integration, or (3) the integral has an obsession for fruit-scented candles. As the final condition is often difficult to measure, most mathematicians are satisfied with the first two.
Consider the integral 
The upper limit of integration causes the expression to be undefined. How can you find the area beneath a curve when x = 3 if the curve doesn’t exist at 3? This is an interesting question. To counter the dilemma, we will evaluate the limit as x approaches 3. To be completely mathematically accurate, we will evaluate the limit as x approaches 3 from the left (since those left-hand values are in our interval of [0,3] but the right-hand values are not).
Example 13: Evaluate 
Solution: Since the integration limit of 3 causes trouble, you substitute a constant (we will use b since it is the upper limit) for it and rewrite the integral as follows:
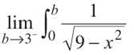
For now, ignore the limit and evaluate the integral.
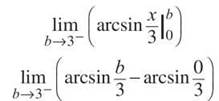
Since arcsin 0 = 0, the integral is simply arcsin b/3. It’s time to bring that limit back into the picture (to evaluate it, you just substitute 3 in for b).
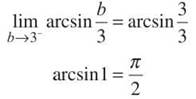
As you can see, the method was quite easy. The problem limit is replaced by a constant, and you let that constant approach the problem limit. The next example involves another tricky integration boundary, but the resulting limit is a little more complicated.
Example 14: Evaluate 
Solution: This is an improper integral because In v has an infinite discontinuity when x = 0. Therefore, we replace the 0 boundary with a constant as follows:
We know the integral of ln x from problem 5 of the integration by parts section.
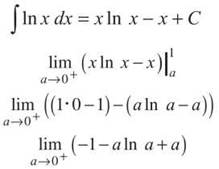
NOTE. The fact that we were finding the limit from the left really didn’t affect the integral at all.
Now it’s time to let a approach 0. The only difficult part of the above is 
Did you notice that this is the indeterminate form of 0-o° ? You can rewrite the limit as
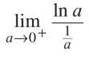
and apply L’Hopital’s Rule. This is the only difficult step in the problem, but it’s a doozy. If you find the derivative of the numerator and denominator, you get
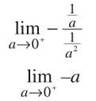
which is definitely 0. That eliminates the hardest part of the expression.
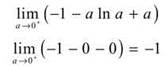
The final answer is —1. If this seemed like a bunch of smoke and mirrors rather than a real magic trick, evaluate the integral with your graphing calculator to see that we’re right—remember that the calculator only gives you an approximation!
We have yet to discuss the other major type of improper integral—an integral that actually has ∞ as one of the limits of integration. You’ll be glad to hear that the process used to solve those integrals is identical to the process we have used in the previous two examples.
Example 15: Evaluate 
Solution: You may think that the answer is automatically ∞. We are integrating from x = 1 all the way to x = ∞, for goodness sakes! Can a shape with an infinite boundary have a finite area? This one will. (I hope I didn’t ruin the suspense. If you think I did, the answer is 1/3—so there, I ruined even more of the suspense.)
The first step to solving this problem is to introduce a constant in place of the troublesome boundary.
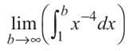
Integrate as usual and then apply the limit.
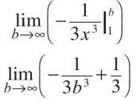
As b goes to infinity, 3b3 will become mega-gigantic, which makes 1/3b3 really tiny, or essentially 0.
0 + 1/3
Therefore, the definite integral is equal to 1/3, and I’m sorry I ruined the surprise.
TIP. Not all shapes with infinite boundaries have finite area. If the area is not finite, the integral is said to diverge, whereas a finite integral is said to converge.
Example 15 highlights a very important characteristic of improper integrals. Any improper integral of the form
(where the exponent p is a real number) will always converge (result in a finite or numerical answer) if p > 1. If, however, p ≤ 1, the integral will not have a numerical answer (the corresponding area is infinite), and the integral is termed divergent. Therefore, you can tell without any work that 
converges (although you’ll have to work it out to determine the actual value), whereas 
will diverge. This is sometimes called the p-test.
The final thing the AP test expects you to do with improper integrals is to compare them with other improper integrals. In such cases, the test will not ask you to evaluate an integral but rather ask you to determine its convergence or divergence. Rather than spending the time to integrate these, it’s best to find an integral that is extremely similar to those that are much easier to work with.
Example 16: Does e 
converge or diverge?
Solution: Compare this to 
(which is similar but much easier to integrate). Because the range of sin x is [—1,1], multiplying e-x by sin x will never give you a result larger than e-x. The most you are multiplying e-x by is 1, and that will return the same value (of course). Otherwise, you are multiplying e-x by a number smaller than one, and the result will be less than e-x. Therefore, we can unequivocally say that
NOTE. For fa ns of bathroom humor, it should come as no surprise that the p-test relies so heavily on number one. I will not elaborate...
Why is this important? We can show that 
is a finite area, so if the original area is less than a finite area, it must also be a finite area and, therefore, converge. All that remains is to actually show that is finite through improper integration.
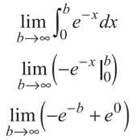
—e-∞ is essentially 0 (to visualize this, graph —ex and let x approach —∞), but e0 equals 1, so the limit is
0 + 1 = 1
Because 
converges, then 
(being smaller) must converge.
EXERCISE 5
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
USE A GRAPHING CALCULATOR TO CHECK YOUR WORK ON THESE PROBLEMS ONLY.
For problems 1 through 4, determine whether or not the improper integrals converge; if they do, evaluate them.
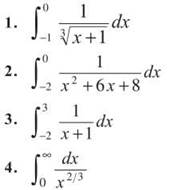
5. Determine whether or not 
converges by comparing it to another, simpler improper integral.
ANSWERS AND EXPLANATIONS
1. The lower limit of integration, —1, is the troublemaker here. Replace it with a constant and evaluate the limit:
To integrate, use «-substitution with u = (x + 1):
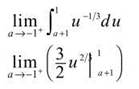
Don’t forget the u boundaries.
When you evaluate the limit, you essentially plug —1 in for a to get
2. If you factor the denominator into (x + 4)(x + 2), you can see that the integration limit of —2 will cause the fraction to be undefined, making the integral improper.
You’ll have to use partial fractions to integrate.
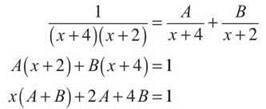
This creates the system A + B = 0 and 2A + 4B = 1. The solution to the system is A = —1/2 and B = 1/2. Substitute these into the expanded integral and solve to get
There is still a problem, however. When you substitute —2 into ln lx + 2l, the expression is still undefined. Our method could not correct the problems inherent in the integral, so the integral is divergent.
3. The infinite discontinuity in this integral does not occur at the endpoints but rather when x = —1. However, you need the discontinuity to exist at an endpoint to use the method you’ve practiced and know so well. Therefore, you can rewrite the integral (using a property of definite integrals) as a sum of smaller integrals, each with —1 as a limit of integration:
Each of these integrals needs to be done separately.
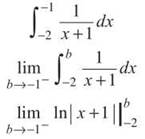
As you continue to solve this, you will end up with ln (—1 + 1) = ln 0, which is undefined. Therefore, this integral is divergent. (The same problem will occur as you integrate the second integral.)
4. Replace that infinite boundary with a constant and integrate.
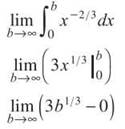
The function 3b1/3 (three times the cube root function) will grow infinitely large as o, so this integral diverges.
5. Compare this integral to 
Because 
Therefore, if you can prove 
has a finite area (and is thus convergent), our original integral must also be convergent.
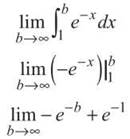
You know from Example 16 that 
Therefore, the original integral 
must also converge.