Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 10. Differential Equations

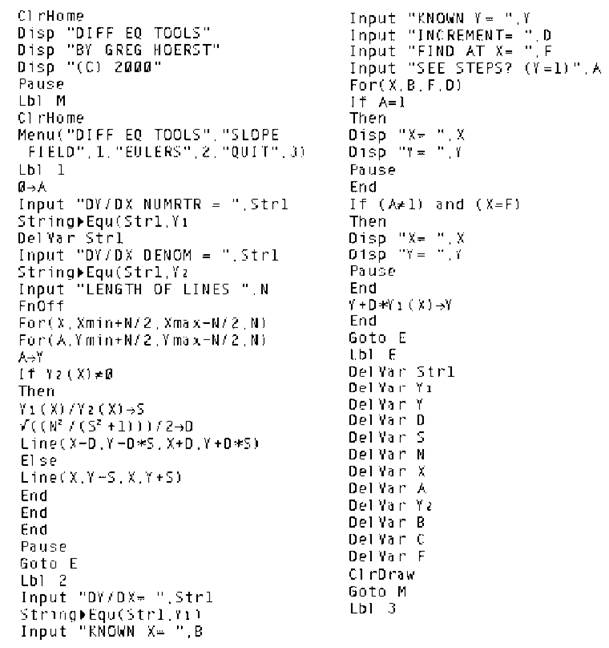
TECHNOLOGY: A DIFFERENTIAL EQUATIONS CALCULATOR PROGRAM

NOTE. You may use this program as long as you type it in exactly as listed, including the author’s name and copyright date. Do not sell this program to anyone—it is meant to be free.

BC students may be a little disappointed in the BC topics so far. All of them seem to be very computational in nature. Arc lengths, slope fields, etc., are all basically formulas you have to memorize. Even worse, the major BC topic in differential equations (Euler’s Method) requires mindless, repetitive work. Luckily, the calculator can save the day.

Thanks to Greg Hoerst, a former 5-er on the BC test and a student of mine, your calculator can help drag you through the doldrums of slope fields and Euler’s Method. Some students were so appreciative of Greg’s program, they set up small shrines in their basement in honor of him, and have voted for him as a write-in candidate for every presidential election ever since.

At the end of this section, you’ll find a relatively short program that will take the drudgery out of Euler’s and slope fields. All you have to do is type in some basic information, and the calculator takes care of the rest. Does this mean you shouldn’t know the formulas and techniques for the two methods it simplifies? No, no, no! Essentially half of the AP test is now done without a calculator, so make sure you don’t grow too dependent on the calculator. If you’d rather not type the program in, and you (or your teacher) have a TI Graphlink that hooks into your computer, you can download the program from my Web site www.calculus-help.com.

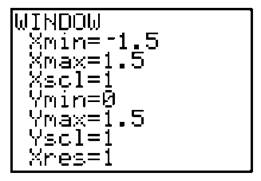
Example 6: Let’s look back at the differential equation you graphed its slope field back in Hands-on Activity 10.2. Of course graphing it with the calculator will be significantly easier. Before we run the program, make sure to set the window you want. In the exercises, we used an x interval of [—1.5,1.5] and a y interval of [0,1.5]. Push the [Window] button, and enter these values into the appropriate spots.

Now, run the program by pressing [Prgm], pressing [Enter] to select the program, and then pressing [Enter] again; you should see the title screen. Press [Enter] to go to the menu, and select “Slope Field.”

The program now asks you to type the numerator and denominator separately. In this example, the denominator is simply 1. Use the [Alpha] button to get X and Y. The program then asks you what the length of the line segments should be. Because this window setting is so detailed, you should use a small number; I used length = .25. On larger windows, you will need to use a larger length, such as 1.

Now, wait as the calculator draws the slope field for you. Once it’s finished, press [Enter] to return to the menu screen.

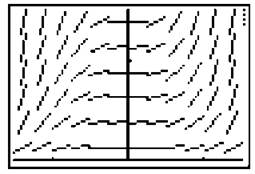
The only drawback to this program is that you can’t tell the calculator exactly where to draw the line segments, but in the grand scheme of things, that matters little. If you have a PC, go to the Web site www.graphmatica.com and download the program Graphmatica. It draws incredible slope fields and easily draws solution graphs to a slope field when you click the initial point (x,y).

Example 7: Use Euler’s Method to approximate y(6) for given that y(5) = 2; use three steps of size ∆x = 1/3.

Solution: This is one of the problems following the section on Euler’s method. Let’s solve it with the calculator. Run the program, and select “Eulers” from the menu. Enter all the information requested by the program. The “Known X” and “Known Y” prompts correspond to the point (x,y) that is on the solution to the differential equation; in this case, that point is (5,2). Before it begins its calculations, the program asks “See Steps? (Y = 1). If you want to see each step of Euler’s method, press [1] and then press [Enter], If you just want the solution, press any other number and press [Enter], Press [1] so we can see all of the steps.

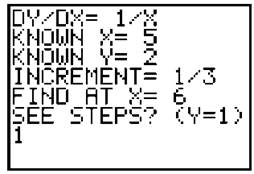
The calculator begins with the given point and takes a step toward the final approximation each time you press [Enter].

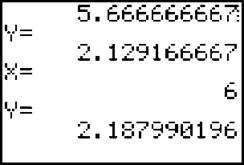
The answer is 2.188, which matches the answer we got the hard way.

Differential Equation Tools, By Greg Hoerst

EXERCISE 6

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

YOU MAY USE A GRAPHING CALCULATOR FOR PROBLEMS 5 THROUGH 8.

1. If f"(x) = 3x + 1, f'(1) = 2, and f(2) = 3, find f(x).

2. Which conic section is the solution to the differential equation Justify your answer mathematically.

3. What is the position function of a particle moving along the x-axis with velocity if the particle passes through the origin when t = 2?

4. If

(a) draw the slope field for dy/dx at all indicated points on the axes below.

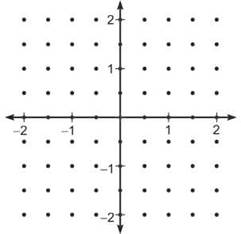
*(b) use Euler’s Method to approximate y(2) using 4 steps if y(0) = 1.

5. A human zygote consists of 1 cell at conception, and the number of cells grows to 8 by the end of one week. Assuming that the rate of cell increase is proportional to the number of cells, how many weeks will it take the babv-in-process to amass 1,000 cells?

ALERT! Problems 7 and 8 represent neither straightforward exponential nor logistic growth. You have to begin with the differential equation expressed in the problem.

*6. Sarah likes mollies above all other tropical fish. Her fish must really like each other, because they are reproducing like crazy. The rate of increase of the fish is proportional to both the population and the number of additional fish the tank could support. Her tank has a carrying capacity of 50 mollies. If she bought 10 fish to start the tank two months ago (none of which died) and has 25 fish now, how many fish will she have in one month?

7. Newton’s Law of Cooling states that an object cools down at a rate proportional to the difference between its temperature and the temperature of the ambient (surrounding) air. If my coffee was 100°F ten minutes ago, the temperature of my room is a constant 75°F, and the coffee is only 90°F now, what will the temperature of my coffee be in 15 minutes?

8. James’ Diabolical Challenge: The population of a species of jellyfish in a small harbor, appropriately called Sting Harbor, is directly proportional to 450 — Q(t), where Q is the population (in thousands) and t is the time (in years). At t = 0 (1990) the population was 100,000, and in 1992, the population was 300,000.

(a) What was the population in 1993?

(b) In what year did the population reach 400,000?

*a BC-only question

ANSWERS AND EXPLANATIONS

1. First, fin d f’(x) by integrating f"(x):

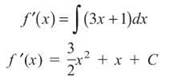
Since you know that f'(1) = 2, use that information to find C.

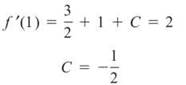
Now, repeat the process to find f(x).

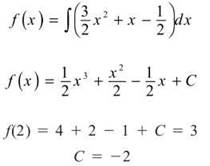
Therefore,

2. Solve this differential equation by separating the variables.

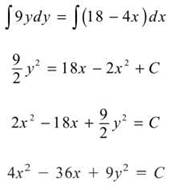
This is an ellipse, since the squared terms have unlike coefficients with the same sign. There’s no need to put it in standard form.

3. We are looking for s(t) knowing that s(t) = ∫v(t)dt and s(2) = 0.

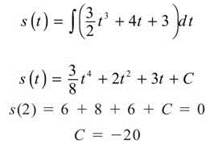
Therefore, the position equation is

4. (a)

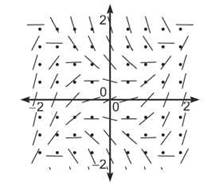
(b) Start at point (0,1), and take 4 steps of size ∆x = 1/2.

Point (0,1): The new point will be (0 + 12, 1 - 12)

Point (1/2,1/2): The new point will be

Point (1,1/2): The new point will be

Point (3/2,7/8): The new point will be

The approximation given by Euler’s method is

5. Because of the proportional relationship described, it’s time to use Nekt. Clearly, the initial value (N) is 1; find k if t is measured in weeks.

You can write k as a decimal, but for once, k is not messy in its exact form, so you can leave it for now. Time to find t when y = 1,000:

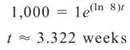
That baby’s growing like a weed.

6. This situation calls for a logistic growth model, and we know that y(0) = 10 (if t equals two months ago):

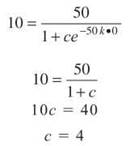
Now, use c and the fact that y(2) = 25 to find k:

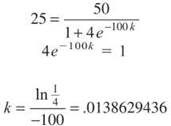
The problem asks us to find y (number of fish) when t = 3 (one month from now):

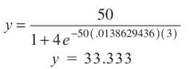
Sarah will have 33 fish and some fish “on the way.”

7. If the rate of change of the temperature is proportional to the difference between the temperature and the ambient air, then this translates to the differential equation

where y is temperature of the cooling object, R is the room temperature, and k is the constant of proportionality. You cannot use y = Ne^kt or logistic growth to model the temperature, as the rate of growth is not proportional to the temperature. However, it is not difficult to translate the given information into the above differential equation. Since R is 75, let’s plug it in and then solve by separation of variables.

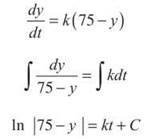
Use the fact that y(0) = 100 (temperature 10 minutes ago) to find C:

Now, use C and the fact that y(10) = 90 to find k:

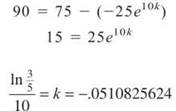
The temperature of my coffee 15 minutes later (t = 25) will be

ALERT! Remember that Q is in thousands, so don't write unnecessary zeros.

8. Much like problem 7, this problem translates into the differential equation

If you solve it using separation of variables, you get

Q = 450 - Ce^kt

Now, use the fact that Q(0) = 100 to find that C = 350. Then, use the fact that Q(2) = 300 to find k:

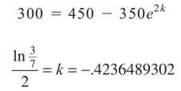
Now we can solve the individual parts of the question,

(a) Find Q if t = 3:

There should be almost 352,000 jellyfish in Sting Harbor.

b) We want to find t when Q = 400:

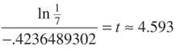
The population will reach 400,000 during mid-1994.

SUMMING IT UP

• A differential equation is simply an equation that contains a derivative.

• Your typical goal in a differential equation problem is to find the equation that has the given derivative; in other words, you are trying to find an antiderivative.

• You will use your calculator a lot in Euler’s Method. If you are allowed to use a calculator to answer an Euler’s Method question on the free response section, you still have to show your work and the setup.