Calculus AB and Calculus BC

CHAPTER 8 Further Applications of Integration

Concepts and Skills

In this chapter, we will review many ways that definite integrals can be used to solve a variety of problems, notably distance traveled by an object in motion along a line. We’ll see that in a variety of settings accumulated change can be expressed as a Riemann sum whose limit becomes an integral of the rate of change.

For BC students, we’ll expand our discussion of motion to include objects in motion in a plane along a parametrically defined curve.

A. MOTION ALONG A STRAIGHT LINE

If the motion of a particle P along a straight line is given by the equation s = F(t), where s is the distance at time t of P from a fixed point on the line, then the velocity and acceleration of P at time t are given respectively by

This topic was discussed as an application of differentiation. Here we will apply integration to find velocity from acceleration and distance from velocity.

Distance

If we know that particle P has velocity v(t), where v is a continuous function, then the distance traveled by the particle during the time interval from t = a to t = b is the definite integral of its speed:

If v(t) 0 for all t on [a, b] (i.e., P moves only in the positive direction), then (1) is equivalent to similarly, if v(t) 0 on [a, b] (P moves only in the negative direction), then (1) yields If v(t) changes sign on [a, b] (i.e., the direction of motion changes), then (1) gives the total distance traveled. Suppose, for example, that the situation is as follows:

Then the total distance traveled during the time interval from t = a to t = b is exactly

The displacement or net change in the particle’s position from t = a to t = b is equal, by the Fundamental Theorem of Calculus (FTC), to

EXAMPLE 1

If a body moves along a straight line with velocity v = t³ + 3t², find the distance traveled between t = 1 and t = 4.

SOLUTION:

Note that v > 0 for all t on [1, 4].

EXAMPLE 2

A particle moves along the x-axis so that its velocity at time t is given by v(t) = 6t² − 18t + 12.

(a) Find the total distance covered between t = 0 and t = 4.

(b) Find the displacement of the particle from t = 0 to t = 4.

SOLUTIONS:

(a) Since v(t) = 6t² − 18t + 12 = 6(t − 1)(t − 2), we see that:

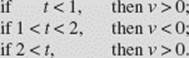
Thus, the total distance covered between t = 0 and t = 4 is

When we replace v(t) by 6t² − 18t + 12 in (2) and evaluate, we obtain 34 units for the total distance covered between t = 0 and t = 4. This can also be verified on your calculator by evaluating

This example is the same as Example 26, in which the required distance is computed by another method.

(b) To find the displacement of the particle from t = 0 to t = 4, we use the FTC, evaluating

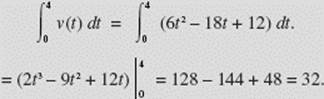
This is the net change in position from t = 0 to t = 4, sometimes referred to as “position shift.” Here it indicates the particle ended up 32 units to the right of its starting point.

EXAMPLE 3

The acceleration of an object moving on a line is given at time t by a = sin t; when t = 0 the object is at rest. Find the distance s it travels from t = 0 to

SOLUTION: Since it follows that

Also, v(0) = 0 yields C = 1. Thus v(t) = 1 − cos t; and since cos t 1 for all t we see that v(t) 0 for all t. Thus, the distance traveled is