Burn Math Class: And Reinvent Mathematics for Yourself (2016)
Act III
6. Two in One
6.5. Reunion
1.In this chapter, we wrote down an abbreviation for the area under a curvy thing, namely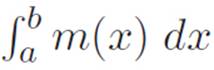 
. This abbreviation reflects the fact that we can think of a curvy area as the sum (hence the S-like ∫ thing) of an infinite number of infinitely thin rectangles (hence the m(x)dx), but it didn’t tell us how to actually calculate curvy areas.
2.Eventually, we realized that if we thought of the m in 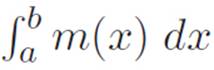as the derivative of some other machine M, then we could rewrite the curvy area as 
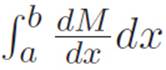, and cancel the dx’s. Since dM was our abbreviation for M(x + dx) − M(x), we knew that 
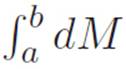must be the sum of all the tiny changes in height as we walk from x = a to x = b, which is to say M(b) − M(a). That is:
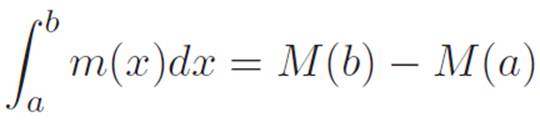
where M is any machine whose derivative is m (an “anti-derivative” of m). We called this the “fundamental hammer of calculus,” since it relates our old idea (the derivative) to our new idea (the integral) and shows us a sense in which they are opposites.
3.We tested the fundamental hammer in a few simple cases where we could compute the required areas without any calculus. In each case, the fundamental hammer gave us the results we expected, which gave us a bit more confidence that our derivation of it made sense.
4.We found that any given machine has infinitely many anti-derivatives, but in a boring sense that doesn’t make integrals any harder to compute, and doesn’t make the fundamental hammer any harder to use. That is, if M is an “anti-derivative” of m, so that M′(x) = m(x), then all the machinesM(x) + # are also anti-derivatives of m.
5.We found that each of the derivative hammers we invented in Chapters 2 and 3 had a partner “anti-hammer” that told us about integration. We proceeded to invent anti-hammers for addition, multiplication, and reabbreviation, each of which “undoes” the original hammer with the same name.
6.We discovered that there is another sense in which derivatives and integrals are opposites, which essentially amounted to a second way of writing the fundamental hammer. That was
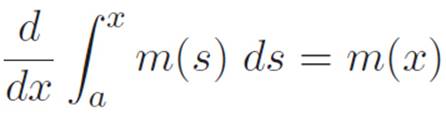
Therefore, our two calculus concepts can be thought of as opposites, irrespective of the order in which we apply them.
7.We turned our attention to the problem of curvy lengths and found that this too involved integration. We zoomed in infinitely far and used the formula for shortcut distances to discover that the length of a machine m’s graph between two points x = a and x = b was
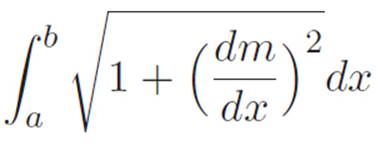
Having reduced the problem of finding curvy lengths to the problem of computing an integral (just like we did for curvy areas), we chose not to focus on a bunch of specific examples of how to compute curvy lengths. Since both problems are now phrased in the language of integrals, any skill we develop on one of these problems immediately carries over to the other. As such, we choose instead to forge ahead into new territory.