What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

1. General Theory

The concept of a class or set of objects is one of the most fundamental in mathematics. A set is defined by any property or attribute which each object considered must either possess or not possess; those objects which possess the property form a corresponding set A. Thus, if we consider the integers, and the property is that of being a prime, the corresponding set A is the set of all primes 2, 3, 5, 7, · · ·.

The mathematical study of sets is based on the fact that sets may be combined by certain operations to form other sets, just as numbers may be combined by addition and multiplication to form other numbers. The study of operations on sets comprises the “algebra of sets,” which has many formal similarities with, as well as differences from, the algebra of numbers. The fact that algebraic methods can be applied to the study of non-numerical objects like sets illustrates the great generality of the concepts of modern mathematics. In recent years it has become apparent that the algebra of sets illuminates many branches of mathematics such as measure theory and the theory of probability; it is also helpful in the systematic reduction of mathematical concepts to their logical basis.

In what follows, I will denote a fixed set of objects of any nature, called the universal set or universe of discourse, and A, B, C, · · · will denote arbitrary subsets of I. If I denotes the set of all integers, A may denote the set of all even integers, B the set of all odd integers, C the set of all primes, etc. Or I might denote the set of all points of a fixed plane, A the set of all points within some circle in the plane, B the set of all points within some other circle in the plane, etc. For convenience we include as “subsets” of I the set I itself and the “empty set” O which contains no elements. The aim of this artificial extension is to preserve the rule that to each property corresponds the subset A of all elements of I possessing this property. In case is some universally valid property such as the one specified by the trivial equation x = x, the corresponding subset of Iwill be I itself, since every object satisfies this equation, while if is some self-contradictory property like x ≠ x, the corresponding subset will contain no objects, and may be denoted by the symbol O.

The set A is said to be a subset of the set B if there is no object in A that is not also in B. When this is the case we write

A ⊂ B or B ⊃ A.

For example, the set A of all integers that are multiples of 10 is a subset of the set B of all integers that are multiples of 5, since every multiple of 10 is also a multiple of 5. The statement A ⊂ B does not exclude the possibility that B ⊂ A. If both relations hold, we say that the sets A and B are equal, and write

A = B.

For this to be true every element of A must be an element of B, and conversely, so that the sets A and B contain exactly the same elements.

The relation A ⊂ B has many similarities with the order relation a ≤ b between real numbers. In particular, it is true that

1) A ⊂ A.

2) If A ⊂ B and B ⊂ A, then A = B.

3) If A ⊂ B and B ⊂ C, then A ⊂ C.

For this reason we also call the relation A ⊂ B an “order relation.” Its chief difference from the relation a ≤ b for numbers is that, while for every pair of numbers a and b at least one of the relations a ≤ b or b ≤ a always holds, this is not true for sets. For example, if A denotes the set consisting of the integers 1, 2, 3,

A = {1, 2, 3},

and B the set consisting of the integers 2, 3, 4,

B= {2, 3, 4},

then neither A ⊂ B nor B ⊂ A. For this reason, the relation A ⊂ B is said to determine a partial ordering among sets, whereas the relation a ≤ b determines a complete ordering among numbers.

In passing, we may remark that from the definition of the relation A ⊂ B it follows that

4) O ⊂ A for any set A, and,

5) A ⊂ I,

where A is any subset of the universe of discourse I. The relation 4) may seem somewhat paradoxical, but it is in agreement with a strict interpretation of the definition of the sign ⊂. For the statement O ⊂ A could be false only if the empty set O contained an object not in A, and since the empty set contains no objects at all, this is impossible no matter what the set A.

We shall now define two operations on sets which have many of the algebraic properties of ordinary addition and multiplication of numbers, though they are conceptually quite distinct from those operations. To this end, let A and B be any two sets. By the “union” or “logical sum” of Aand B we mean the set which consists of all the objects which are in either A or B (including any that may be in both). This set we denote by the symbol A + B. By the “intersection” or “logical product” of A and B we mean the set consisting only of those elements which are in both A and B. This set we denote by the symbol A. B or simply AB. To illustrate these operations, we may again choose as A and B the sets

    A = {1, 2, 3),   B = {2, 3, 4}.

Then  A + B = {1, 2, 3, 4},  AB = {2, 3}.

Among the important algebraic properties of the operations A + B and AB we list the following. They should be verified by the reader on the basis of the definition of these operations:

6) A + B = B + A

7) AB = BA

8) A + (B + C) = (A + B) + C

9) A(BC) = (AB)C

10) A + A = A

11) AA = A

12) A(B + C) = (AB + AC)

13) A + (BC) = (A + B)(A + C)

14) A + O = A

15) AI = A

16) A + I = 1

17) AO = O

18) the relation A ⊂ B is equivalent to either of the two relations A + B = B, AB = A.

The verification of these laws is a matter of elementary logic. For example, 10) states that the set consisting of those objects which are either in A or in A is precisely the set A, while 12) states that the set consisting of those objects which are in A and also in either B or C is the same as the set consisting of those objects which are either in both A and B or in both A and C. The logical reasoning involved in this and other arguments may be illustrated by representing the sets A, B, C as areas in a plane, provided that one is careful to provide for all the possibilities of the sets involved having elements distinct from and in common with each other.

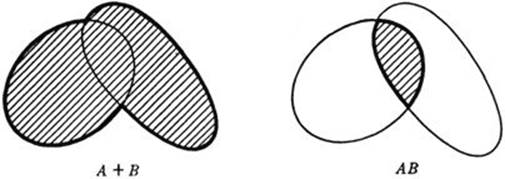
Fig. 26. Union and intersection of sets.

The reader will have observed that the laws 6, 7, 8, 9, and 12 are identical with the familiar commutative, associative, and distributive laws of algebra. It follows that all rules of the ordinary algebra of numbers which are consequences of the commutative, associative, and distributive laws are also valid in the algebra of sets. The laws 10, 11, and 13, however, have no numerical analogs, and give the algebra of sets a simpler structure than the algebra of numbers. For example, the binomial theorem of ordinary algebra is replaced in the algebra of sets by the equality

(A + B)ⁿ = (A + B).(A + B)· · · · ·(A + B) = A + B

which is a consequence of 11. Laws 14, 15, and 17 indicate that the properties of O and I with respect to union and intersection of sets are largely similar to the properties of the numbers 0 and 1 with respect to ordinary addition and multiplication. Law 16 has no analog in the algebra of numbers.

It remains to define one further operation in the algebra of sets. Let A be any subset of the universal set I. Then by the complement of A in I we mean the set which consists of all the objects in I which are not in A. This set we denote by the symbol A′. Thus if I is the set of all natural numbers and A the set of primes, A′ consists of 1 and the composites. The operation A′, which has no exact analog in the algebra of numbers, possesses the following properties:

19) A + A′ = I

20) AA′ = O

21) O′ = I

22) I′ = O

23) A″ = A

24) The relation A ⊂ B is equivalent to the relation B′ ⊂ A′.

25) (A + B)′ = A′B′

26) (AB)′ = A′ + B′.

Again we shall leave the verification of these laws to the reader.

The laws 1 to 26 form the basis of the algebra of sets. They possess the remarkable property of “duality,” in the following sense:

If in any one of the laws 1 to 26 the symbols

⊂ and ⊃

O and I

+ and ⋅

are everywhere interchanged (insofar as they appear), then the result is again one of these laws.

For example, the law 6 becomes 7, 12 becomes 13, 17 becomes 16, etc. It follows that to any theorem which can be proved on the basis of the laws 1 to 26 there corresponds another, “dual,” theorem, obtained by making the interchanges above. For, since the proof of any theorem will consist of the successive application at each step of certain of the laws 1 to 26, the application at each step of the dual law will provide a proof of the dual theorem. (For a similar duality in geometry, see Chapt. IV.)

2. Application to Mathematical Logic

The verification of the laws of the algebra of sets rested on the analysis of the logical meaning of the relation A ⊂ B and the operations A + B, AB, and A′. We can now reverse this process and use the laws 1 to 26 as the basis for an “algebra of logic.” More precisely, that part of logic which concerns sets, or what is equivalent, properties or attributes of objects, may be reduced to a formal algebraic system based on the laws 1 to 26. The logical “universe of discourse” defines the set I; each property or attribute of objects defines the set A consisting of all objects in Iwhich possess this attribute. The rules for translating the usual logical terminology into the language of sets may be illustrated by the following examples:

“Either A or B”    A + B

“Both A and B”    AB

“Not A”    A′

“Neither A nor B”    (A + B)′, or equivalently, A′B′

“Not both A and B”    (AB)’, or equivalently, A’ + B’

“All A are B” or “If A then B” or “A implies B” A ⊂ B

“Some A are B”    AB ≠ O

“No A are B”    AB = O

“Some A are not B”    AB ′ ≠ O

“There are no A”    A = O

In terms of the algebra of sets, the syllogism “Barbara,” which states: “If all A are B, and all B are C, then all A are C,” becomes simply

3) If A ⊂ B and B ⊂ C then A ⊂ C.

Likewise, the “law of contradiction,” which states: “An object cannot both possess an attribute and not possess it,” becomes

20) A A’ = O,

while the “law of excluded middle” which states: “An object must either possess a given attribute or not possess it” becomes

19) A + A′ = I.

Thus the part of logic which is expressible in terms of the symbols ⊂, +, ·, and ′ can be treated as a formal algebraic system, subject to the laws 1 to 26. This fusion of the logical analysis of mathematics with the mathematical analysis of logic has resulted in the creation of a new discipline,mathematical logic, which is now in the process of vigorous development.

From the point of view of axiomatics, it is a remarkable fact that the statements 1 to 26, together with all other theorems of the algebra of sets, can be deduced from the following three equations:

    A + B = B + A

27)    (A + B) + C = A + (B + C)

    (A′ + B′)′ + (A′ + B)′ = A.

It follows that the algebra of sets can be constructed as a purely deductive theory like Euclidean geometry on the basis of these three statements taken as axioms. When this is done, the operation AB and the order relation A ⊂ B are defined in terms of A + B and A′:

AB means the set (A′ + B′)′

A ⊂ B means that A + B = B.

A quite different example of a mathematical system satisfying all the formal laws of the algebra of sets is provided by the eight numbers 1, 2, 3, 5, 6, 10, 15, 30, where a + b is defined to mean the least common multiple of a and b, ab the greatest common divisor of a and b, a ⊂ b the statement “a is a factor of b,” and a′ the number 30/a. The existence of such examples has led to the study of general algebraic systems satisfying the laws 27). These systems are called “Boolean algebras” in honor of George Boole (1815-1864), an English mathematician and logician whose book, An Investigation of the Laws of Thought, appeared in 1854.

3. An Application to the Theory of Probability

The algebra of sets greatly illuminates the theory of probability. To consider only the simplest case, let us imagine an experiment with a finite number of possible outcomes, all of which are assumed to be “equally likely.” The experiment may, for example, consist of drawing a card at random from a well-shuffled deck of 52 cards. If the set of possible outcomes of the experiment is denoted by I, and if A denotes any subset of I, then the probability that the outcome of the experiment will belong to the subset A is defined to be the ratio

If we denote the number of elements in any set A by the symbol n(A), then this definition may be written in the form

(1)    

In our example, if A denotes the subset of hearts, then n(A) = 13, n(I) = 52, and .

The concepts of the algebra of sets enter into the calculation of probabilities when the probabilities of certain sets are known and the probability of others are required. For example, from a knowledge of p(A), p(B), and p(AB) we may compute the probability of p(A + B):

(2)   p(A+ B) = p(A) + p(B) – p{AB).

The proof is simple. We have

n(A + B) = n(A) + n(B) – n(AB),

since the elements common to A and B, i.e. the elements in AB, will be counted twice in the sum n(A) + n(B), and hence we must subtract n(AB) from this sum in order to obtain the correct count for n(A + B). Dividing each term of this equation by n(I), we obtain equation (2).

A more interesting formula arises when we consider three subsets, A, B, C, of I. From (2) we have

p(A + B + C) = p[(A + B) + C] = p(A + B) + p(C) – p[(A + B)C].

From (12) of the preceding section we know that (A + B)C = AC + BC: Hence

p[(A + B)C] = p(AC + BC) = p(AC) + p(BC) – p(ABC).

Substituting in the previous equation this value for p[(A + B)C] and the value of p(A + B) given by (2), we obtain the desired formula:

(3) p(A + B + C) = p(A) + p(B) + p(C) – p(AB) – p(AC) – p(BC) + p(ABC).

As an example, let us consider the following experiment. The three digits 1, 2, 3 are written down in random order. What is the probability that at least one digit will occupy its proper place? Let A denote the set of all arrangements in which the digit 1 comes first, B the set of all arrangements in which the digit 2 comes second, and C the set of all arrangements in which the digit 3 comes third. Then we wish to calculate p(A + B + C). It is clear that

for when one digit occupies its proper place there are two possible orders for the remaining digits, out of a total of 3·2·1 = 6 possible arrangements of the three digits. Moreover,

and

since there is only one way in which each of these cases may occur. It follows from (3) that

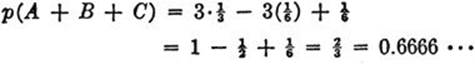
Exercise: Find a corresponding formula for p(A + B + C + D) and apply it to the case of four digits. The corresponding probability is 5/8 = 0.6250.

The general formula for the union of n subsets is

(4)

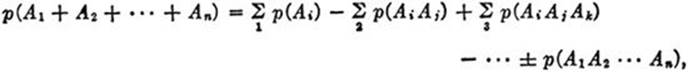
where the symbols stand for summation of the possible combinations of the sets A₁, A₂, · · ·,A_n taken one, two, three, · · ·, (n – 1) at a time. This formula may be established by mathematical induction in precisely the same way that we derived (3) from (2). From (4) it is easy to show that if the n digits 1, 2, 3, · · ·, n are written down in random order, the probability that at least one digit will occupy its proper place is

(5)    

where the last term is taken with a plus or minus sign according as n is odd or even. In particular, for n = 5 the probability is

We shall see in Chapter VIII that as n tends to infinity the expression

tends to a limit, 1/e, whose value to five places of decimals is .36788. Since from (5) p_n = 1 – S_n, this shows that as n tends to infinity

p_n → 1 – 1/e = .63212.