What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)
CHAPTER IV. PROJECTIVE GEOMETRY. AXIOMATICS. NON-EUCLIDEAN GEOMETRIES
APPENDIX. *GEOMETRY IN MORE THAN THREE DIMENSIONS
1. Introduction
The “real space” that is the medium of our physical experience has three dimensions, the plane has two dimensions, and the line one. Our spatial intuition in its ordinary sense is definitely limited to three dimensions. Still, on many occasions it is quite convenient to speak of “spaces” having four or more dimensions. What is the meaning of an n-dimensional space when n is greater than three, and what purposes can it serve? An answer can be given from the analytic as well as from the purely geometric point of view. The terminology of n-dimensional space may be regarded merely as a suggestive geometric language for mathematical ideas that are no longer within reach of ordinary geometric intuition. We shall give a brief indication of the simple considerations that motivate and justify this language.
2. Analytic Approach
We have already remarked on the inversion of meaning which came about in the course of development of analytic geometry. Points, lines, curves, etc. were originally considered to be purely “geometrical” entities, and the task of analytic geometry was merely to assign to them systems of numbers or equations, and to interpret or to develop geometrical theory by algebraic or analytic methods. In the course of time the opposite point of view began increasingly to assert itself. A number x, or a pair of numbers x, y, or a triple of numbers x, y, z were considered as the fundamental objects, and these analytic entities were then “visualized” as points on a line, in a plane, or in space. From this point of view geometrical language serves only to state relations between numbers. We may discard the primary or even the independent character of geometrical objects by saying that a number pair x, y is a point in the plane, the set of all number pairs x, y that satisfy the linear equation L(x, y) = ax + by + c = 0 with fixed numbers a, b, c is a line, etc. Similar definitions may be made in space of three dimensions.
Even if we are primarily interested in an algebraic problem, it may be that the language of geometry lends itself to an adequate brief description of it, and that geometrical intuition suggests the appropriate algebraic procedure. For example, if we wish to solve three simultaneous linear equations for three unknown quantities x, y, z:
L(x, y, z) = ax + by + cz + d = 0
L′(x, y, z) = a′x + b′y + c′z + d′ = 0
L″(x, y, z) = a″x + b″y + c″z + d″ = 0,
we may visualize the problem as that of finding the point of intersection in three dimensional space R3 of the three planes defined by the equations L = 0, L′ = 0, L″ = 0. Again, if we are considering only the number pairs x, y for which x > 0, we may visualize them as the half-plane to the right of the x-axis. More generally, the totality of number pairs x, y for which
L(x, y) = ax + by + d > 0
may be visualized as a half-plane on one side of the line L = 0, and the totality of number triples x, y, z for which
L(x, y, z) = ax + by + cz + d > 0
may be visualized as the “half-space” on one side of the plane L(x, y, z) = 0.
The introduction of a “four-dimensional space” or even an “n-dimensional space” is now quite natural. Let us consider a quadruple of numbers x, y, z, t. Such a quadruple is said to be represented by, or simply, to be a point in four-dimensional space R4. More generally, a point of n-dimensional space Rn is by definition simply an ordered set of n real numbers x1, x2,..., xn. It does not matter that we cannot visualize such a point. The geometrical language remains just as suggestive for algebraic properties involving four or n variables. The reason for this is that many of the algebraic properties of linear equations, etc. are essentially independent of the number of variables involved, or, as we may say, of the dimension of the space of the variables. For example, we call “hyperplane” the totality of all points x1, x2,..., xn in the n-dimensional space Rn which satisfy a linear equation
L(x1, x2,…, xn) = a1x1 + a2x2 + … + anxn + b = 0.
Then the fundamental algebraic problem of solving a system of n linear equations in n unknowns,
L1(x1, x2, · · ·, xn) = 0
L2(x1, x2, · · ·, xn) = 0
............................................
L3(x1, x2, · · ·, xn) = 0
is stated in geometrical language as that of finding the point of inter section of the n hyperplanes L1 = 0, L2 = 0,..., Ln = 0.
The advantage of this geometrical mode of expression is only that it emphasizes certain algebraic features which are independent of n and which are capable of visualization for n ≤ 3. In many applications the use of such a terminology has the advantage of abbreviating, facilitating, and directing the intrinsically analytic considerations. The theory of relativity may be mentioned as an example where important progress was attained by uniting the space coördinates x, y, z and the time coördinate t of an “event,” into a four-dimensional “space-time” manifold of numberquadruples x, y, z, t. By the introduction of a non-Euclidean hyperbolic geometry into this analytic framework, it became possible to describe many otherwise complex situations with remarkable simplicity. Similar advantages have accrued in mechanics and statistical physics, as well as in purely mathematical fields.
Here are some examples from mathematics. The totality of all circles in the plane forms a three-dimensional manifold, because a circle with center x, y and radius t can be represented by a point with the coördinates x, y, t. Since the radius of a circle is a positive number, the totality of points representing circles fills out a half-space. In the same way, the totality of all spheres in ordinary three-dimensional space forms a four-dimensional manifold, since each sphere with center x, y, z and radius t can be represented by a point with coördinates x, y, z, t. A cube in three-dimensional space with edge of length 2, sides parallel to the coördinate planes, and center at the origin, consists of the totality of all points x1, x2, x3 for which | x1 | ≤ 1, | x2 | ≤ 1, | x3 | ≤ 1. In the same way a “cube” in n-dimensional space Rn with edge 2, sides parallel to the coördinate planes, and center at the origin, is defined as the totality of points x1, x2,..., xn for which simultaneously
| x1 | ≤ 1, | x2 | ≤ 1, . . ., | xn | ≤ 1.
The “surface” of this cube consists of all points for which at least one equality sign holds. The surface elements of dimension n – 2 consist of those points where at least two equality signs hold, etc.
Exercise: Describe the surface of such a cube in the three-, four-, and n-dimensional cases.
*3. Geometrical or Combinatorial Approach
While the analytical approach to n-dimensional geometry is simple and well adapted to most applications, there is another method of procedure which is purely geometrical in character. It is based on a reduction from n- to (n – 1)-dimensional data that enables us to define geometry in higher dimensions by a process of mathematical induction.
Let us start with the boundary of a triangle ABC in two dimensions. By cutting the closed polygon at the point C and then rotating AC and BC into the line AB we obtain the simple straight figure of Figure 116 in which the point C appears twice. This one-dimensional figure gives a complete representation of the boundary of the two dimensional triangle. By bending the segments AC and BC together in a plane, we can make the two points C coincide again. But, and this is the important point, we need not do this bending. We need only agree to “identify,” i.e. not to distinguish between, the two points C in Figure 116, even though they do not actually coincide as geometrical entities in the naive sense. We may even go a step farther by taking the three segments apart at the points A and B, obtaining a set of three segments CA, AB, BC which can be put together again to form a “real” triangle by making the identified pairs of points coincide. This idea of identifying different points in a set of segments to form a polygon (in this case a triangle) is sometimes very practical. If we wish to ship a complicated framework of steel bars, such as the framework of a bridge, we ship it in single bars and mark by the same symbol those endpoints which are to be connected when the framework is put together in space. The system of bars with marked endpoints is a complete equivalent of the spatial framework. This remark suggests the way to reduce a two-dimensional polyhedron in three-dimensional space to figures of lower dimensions. Let us take, for example, the surface of a cube (Fig. 117). It can be immediately reduced to a system of six plane squares whose boundary segments are appropriately identified, and in another step to a system of 12 straight segments with their endpoints properly identified.
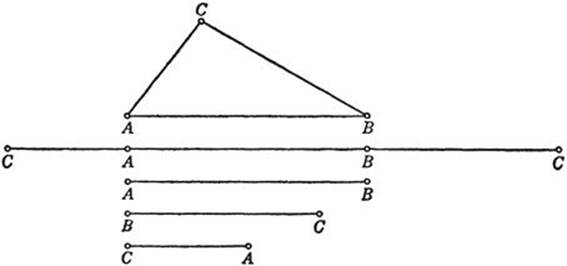
Fig. 116. Triangle defined by segments with coördinated ends.
In general, any polyhedron in three-dimensional space R3 can be reduced in this way either to a system of plane polygons, or to a system of straight segments.
Exercise: Carry out this reduction for all the regular polyhedra (see p. 237).
It is now quite clear that we can invert our reasoning, defining a polygon in the plane by a system of straight segments, and a polyhedron in R3 by a system of polygons in R2 or again, with a further reduction, by a system of straight segments. Hence it is natural to define a “polyhedron” in four-dimensional space R4 by a system of polyhedra in R3 with proper identification of their two-dimensional faces; polyhedra in R5 by systems of polyhedra in R4, and so on. Ultimately we can reduce every polyhedron in Rn to a system of straight segments.
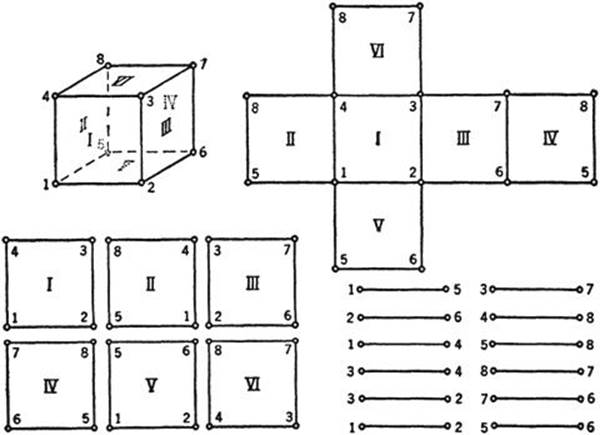
Fig. 117. Cube defined by coördination of vertices and edges.
It is not possible here to develop this subject much further. Only a few remarks without proof may be added. A cube in R4 is bounded by 8 three-dimensional cubes, each identified with a “neighbor” along a two-dimensional face. The cube in R4 has 16 vertices, in each of which four of the 32 straight edges meet. In R4 there are six regular polyhedra. Besides the “cube” there is one bounded by 5 regular tetrahedra, one bounded by 16 tetrahedra, one bounded by 24 octahedra, one bounded by 120 dodecahedra, and one bounded by 600 tetrahedra. For n > 4 dimensions it has been proved that only 3 regular polyhedra are possible: one with n + 1 vertices bounded by n + 1 polyhedra in Rn-1 with n sides of (n – 2) dimensions; one with 2n vertices bounded by 2n polyhedra in Rn–1 with 2n – 2 sides; and one with 2n vertices and 2n polyhedra of n sides in Rn–1 as boundaries.
* Exercise: Compare the definition of the cube in R4 given in Article 2 with the definition given in this article, and show that the “analytical” definition of the surface of the cube of Article 2 is equivalent to the “combinatorial” definition of this article.
From the structural, or “combinatorial,” point of view, the simplest geometrical figures of dimension 0, 1, 2, 3 are the point, the segment, the triangle, and the tetrahedron, respectively. In the interests of a uniform notation let us denote these figures by the symbols T0, T1, T2, T3, respectively. (The subscripts denote the dimension.) The structure of each of these figures is described by the statement that each Tn contains n + 1 vertices and that each subset of i + 1 vertices of a Tn (i = 0, 1, ..., n) determines a Ti. For example, the three-dimensional tetrahedron T3 contains 4 vertices, 6 segments, and 4 triangles.
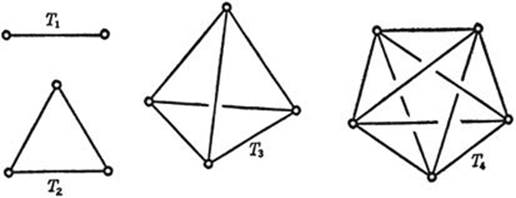
Fig. 118. The simplest elements in 1, 2, 3, 4 dimensions.
It is clear how to proceed. We define a four-dimensional “tetrahedron” T4 as a set of five vertices such that each subset of four vertices determines a T3, each subset of three vertices determines a T2, etc. The schematic diagram of T4 is shown in Figure 118. We see that T4 contains 5 vertices, 10 segments, 10 triangles, and 5 tetrahedra.
The generalization to n dimensions is immediate. From the theory of combinations it is known that there are exactly ![]() different subsets of i objects each that can be formed from a given set of r objects. Hence an n-dimensional “tetrahedron” contains
different subsets of i objects each that can be formed from a given set of r objects. Hence an n-dimensional “tetrahedron” contains
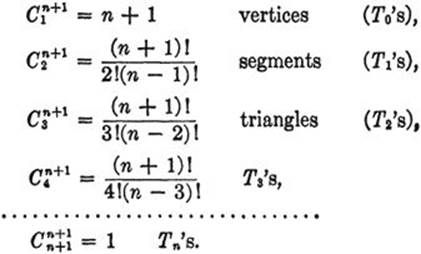
Exercise: Draw a diagram of T5 and determine the number of different Ti’s it contains, for i = 0, 1,..., 5.