What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

**§4. THE PRIME NUMBER THEOREM OBTAINED BY STATISTICAL METHODS

When mathematical methods are applied to the study of natural phenomena one is usually satisfied with arguments in the course of which the chain of strict logical reasoning is interrupted by more or less plausible assumptions. Even in pure mathematics one encounters reasoning which, while it does not provide a rigorous proof, nevertheless suggests the correct solution and points the direction in which a rigorous proof may be sought. Bernoulli’s solution of the brachistochrone problem (see p. 383) has this character, as does most of the early work in analysis.

By a procedure typical of applied mathematics and particularly of statistical mechanics we shall here present an argument that at least makes plausible the truth of Gauss’s famous law of the distribution of the primes. (A related procedure was suggested to one of the authors by the experimental physicist Gustav Hertz.) This theorem, discussed empirically in the supplement to Chapter I, states that the number A(n) of primes not exceeding n is asymptotically equivalent to the quantity n/log n:

By this is meant that the ratio of A(n) to n/log n tends to the limit 1 as n tends to infinity.

We start by making the assumption that there exists a mathematical law which describes the distribution of the primes in the following sense: for large values of n the function A(n) is approximately equal to the integral , where W(x) is a function which measures the “density” of the primes. (We choose 2 as lower limit of the integral because for x < 2 clearly A(x) = 0.) More precisely, let x be a large number and Δx another large number but such that the order of magnitude of x is greater than that of Δx. (For example, we might agree to set .) Then we are assuming that the distribution of the primes is so smooth that the number of primes in the interval from x to x + Δx is approximately equal to W(x)·Δx, and moreover that W(x) as a function of x changes so slowly that the integral may be replaced by a subsequent rectangular approximation without changing its asymptotic value. With these preliminary remarks we are ready to begin the argument.

We have proved (p. 471) that for large integers log n! is asymptotically equal to n·log n,

log n! ∼ n·log n.

Now we proceed by giving a second formula for log n! involving the primes and comparing the two expressions. Let us count how often an arbitrary prime p less than n is contained as a factor in the integer n! = 1·2·3... n. We shall denote by [a]_p the largest integer k such that p^k divides a. Since the prime decomposition of every integer is unique, it follows that [ab]_p = [a]_p + [b]_p for any two integers a and b. Hence

[n!]_p = [1]_p + [2]_p + [3]_p +... + [n]_p.

The terms in the sequence 1, 2, 3,..., n which are divisible by p^k are p^k, 2p^k, 3p^k,...; their number N_K for large n is approximately n/p^k. The number M_k of these terms which are divisible by p^k and no higher power of p is equal to N_K – N_k+1. Hence

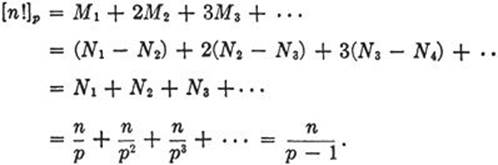
(These equalities are, of course, only approximate.)

It follows that for large n the number n! is given approximately by the product of all the expressions for all primes p < n. Thus we have the formula

Comparing this with our previous asymptotic relation for log n! we find, writing x instead of n,

(1)   

The next and decisive step is to obtain an asymptotic expression in terms of W(x) for the right side of (1). When x is very large we may subdivide the interval from 2 to x = n into a large number r of large subintervals by choosing points 2 = ξ₁, ξ₂,..., ξ_r, ξ_r+1 = x, with corresponding increments Δξ_i = ξ_i+1 – ξ_i. In each subinterval there may be primes, and all the primes in the jth subinterval will have approximately the value ξ_i. By our assumption on W(x) there are approximately W(ξ_i)·Δξ_i primes in the jth subinterval; hence the sum on the right side of (1) is approximately equal to

Replacing this finite sum by the integral which it approximates, we have as a plausible consequence of (1) the relation

(2)  

From this we shall determine the unknown function W(x). If we replace the sign ∼ by ordinary equality and differentiate both sides with respect to x, then by the fundamental theorem of the calculus

(3)    

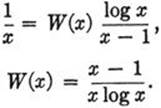
We assumed at the beginning of our discussion that A(x) is approximately equal to ; hence A(x) is approximately given by the integral

(4)    .

In order to evaluate this integral we observe that the function f(x) = x/log x has the derivative

For large values of x the two expressions

are approximately equal, since for large x the second term in both cases will be much smaller than the first. Hence the integral (4) will be asymptotically equal to the integral

since the integrands will be almost equal over most of the range of integration. The term 2/log 2 can be neglected for large x since it is a constant, and thus we obtain the final result

which is the prime number theorem.

We cannot pretend that the preceding argument has more than a suggestive value. But on closer analysis the following fact emerges. It is not difficult to give a complete justification for all the steps that we have so boldly made; in particular, for equation (1), for the asymptotic equivalence between this sum and the integral in (2), and for the step leading from (2) to (3). It is far more difficult to prove the existence of a smooth density function W(x), which we assumed at the beginning. Once we accept this, the evaluation of the function is a comparatively simple matter; from this point of view the proof of the existence of such a function is the central difficulty of the prime number problem.