Nabla Trigonometric Functions - Nabla Fractional Calculus

Discrete Fractional Calculus (2015)

3. Nabla Fractional Calculus

3.4. Nabla Trigonometric Functions

In this section we introduce the discrete nabla hyperbolic sine and cosine functions, the discrete sine and cosine functions and give some of their properties. First we define the nabla hyperbolic sine and cosine functions.

Definition 3.15.

Assume $p,-p \in \mathcal{R}$ . Then the generalized nabla hyperbolic sine and cosine functions are defined as follows:

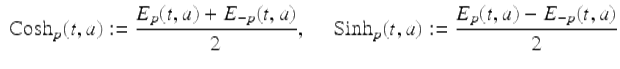
$\displaystyle{\mbox{ Cosh}_{p}(t,a):= \frac{E_{p}(t,a) + E_{-p}(t,a)} {2},\quad \mbox{ Sinh}_{p}(t,a):= \frac{E_{p}(t,a) - E_{-p}(t,a)} {2} }$

for $t \in \mathbb{N}_{a}$ .

The following theorem gives various properties of the nabla hyperbolic sine and cosine functions.

Theorem 3.16.

Assume $p,-p \in \mathcal{R}$ . Then

(i)

$\mbox{ Cosh}_{p}(a,a) = 1,\quad \mbox{ Sinh}_{p}(a,a) = 0;$

(ii)

$\mbox{ Cosh}_{p}^{2}(t,a) -\mbox{ Sinh}_{p}^{2}(t,a) = E_{p^{2}}(t,a),\quad t \in \mathbb{N}_{a};$

(iii)

$\nabla \mbox{ Cosh}_{p}(t,a) = p(t)\;\mbox{ Sinh}_{p}(t,a),\quad t \in \mathbb{N}_{a+1};$

(iv)

$\nabla \mbox{ Sinh}_{p}(t,a) = p(t)\;\mbox{ Cosh}_{p}(t,a),\quad t \in \mathbb{N}_{a+1};$

(v)

$\mbox{ Cosh}_{-p}(t,a) = \mbox{ Cosh}_{p}(t,a),\quad t \in \mathbb{N}_{a};$

(vi)

$\mbox{ Sinh}_{-p}(t,a) = -\mbox{ Sinh}_{p}(t,a),\quad t \in \mathbb{N}_{a}$ .

Proof.

Parts (i), (v), (vi) follow immediately from the definitions of the nabla hyperbolic sine and cosine functions. To see that (ii) holds, note that

$\displaystyle\begin{array}{rcl} & & \mathrm{Cosh}_{p}^{2}(t,a) -\mathrm{ Sinh}_{ p}^{2}(t,a) {}\\ & & = \frac{\left [E_{p}(t,a) + E_{-p}(t,a)\right ]^{2} -\left [E_{p}(t,a) - E_{-p}(t,a)\right ]^{2}} {4} {}\\ & & = E_{p}(t,a)E_{-p}(t,a) {}\\ & & = E_{p\boxplus (-p)}(t,a) {}\\ & & = E_{p^{2}}(t,a). {}\\ \end{array}$

To see that (iii) holds, consider

$\displaystyle\begin{array}{rcl} \nabla \mbox{ Cosh}_{p}(t,a)& =& \frac{1} {2}\nabla E_{p}(t,a) + \frac{1} {2}\nabla E_{-p}(t,a) {}\\ & =& \frac{1} {2}\;[pE_{p}(t,a) - pE_{-p}(t,a)] {}\\ & =& p\;\frac{E_{p}(t,a) - E_{-p}(t,a)} {2} {}\\ & =& p\;\mbox{ Sinh}_{p}(t,a). {}\\ \end{array}$

The proof of (iv) is similar (Exercise 3.13). □

Next, we define the nabla sine and cosine functions.

Definition 3.17.

Assume $ip,-ip \in \mathcal{R}$ . Then we define the nabla sine and cosine functions as follows:

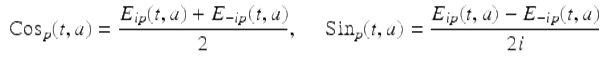
$\displaystyle{\mbox{ Cos}_{p}(t,a) = \frac{E_{ip}(t,a) + E_{-ip}(t,a)} {2},\quad \mbox{ Sin}_{p}(t,a) = \frac{E_{ip}(t,a) - E_{-ip}(t,a)} {2i} }$

for $t \in \mathbb{N}_{a}$ .

Using the definitions of Cos_p(t, a) and Sin_p(t, a) we get immediately Euler’s formula

$\displaystyle{ E_{ip}(t,a) = \mbox{ Cos}_{p}(t,a) + i\mbox{ Sin}_{p}(t,a),\quad t \in \mathbb{N}_{a} }$

(3.11)

provided $ip,-ip \in \mathcal{R}$ .

The following theorem gives some relationships between the nabla trigonometric functions and the nabla hyperbolic trigonometric functions.

Theorem 3.18.

Assume p is a constant. Then the following hold:

(i)

Sin _ip (t,a) = iSinh _p (t,a), if p ≠ ± 1;

(ii)

Cos _ip (t,a) = Cosh _p (t,a), if p ≠ ± 1;

(iii)

Sinh _ip (t,a) = iSin _p (t,a), if p ≠ ± i;

(iv)

Cosh _ip (t,a) = Cos _p (t,a), if p ≠ ± i,

for $t \in \mathbb{N}_{a}$ .

Proof.

To see that (i) holds, note that

$\displaystyle\begin{array}{rcl} \mbox{ Sin}_{ip}(t,a)& =& \frac{1} {2i}[E_{i^{2}p}(t,a) - E_{-i^{2}p}(t,a)] {}\\ & =& \frac{1} {2i}[E_{-p}(t,a) - E_{p}(t,a)] {}\\ & =& i\frac{E_{p}(t,a) - E_{-p}(t,a)} {2} {}\\ & =& i\;\mbox{ Sinh}_{p}(t,a). {}\\ \end{array}$