High School Geometry Unlocked (2016)

Lesson 2.4. Constructing Polygons

EQUILATERAL TRIANGLE

Method 1—Start with Two Points

In this exercise, you’ll use your compass and straightedge to construct an equilateral triangle. The beginning steps are the same as the methods for creating perpendicular lines, seen earlier in this chapter. Therefore, we’ll keep the instructions brief. Feel free to refer to the earlier section on constructing perpendicular lines for more details.

Supplies

For this section, you
should have your compass
and straightedge ready.

Position the compass so that the needle is on point A, and the drawing point is on B. Make an arc above the two points, in the spot where the third vertex of the triangle should go (eyeball it). You can also make a full circle if you prefer.

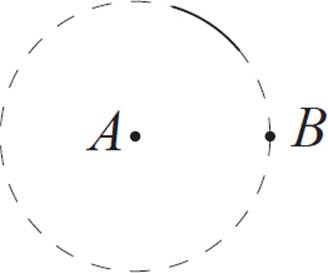
Constructing an
equilateral triangle is very
much like constructing
perpendicular lines! (See
earlier in Lesson 2.3.)

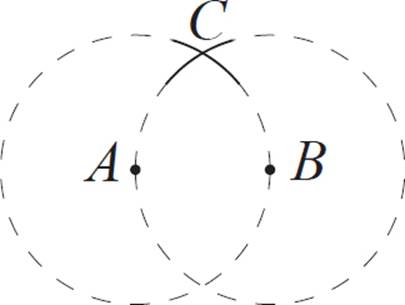
Next, position the compass so that the needle is on point B, and the drawing point is on A. With this radius, make a second arc to intersect the first one. Label this point C.

Finally, connect points A, B, and C to form a triangle. Use your straightedge.

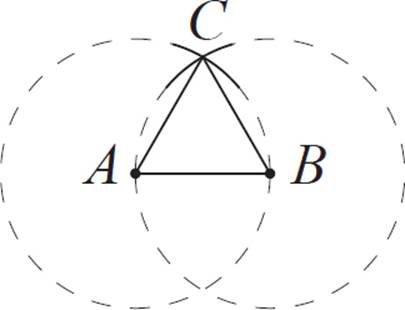
This triangle is equilateral. The reason this works is that the compass radius always matched the distance between A and B, so we know that all three sides are equal.

Try a few more for practice! Follow the steps as above to create an equilateral triangle. Repeat until you’re comfortable with the process.

Method 2—Inscribed in a Circle

For this method, begin with a circle, with a point marked for its center. Label the center point A. Also choose a point on the circle’s circumference, and label it B.

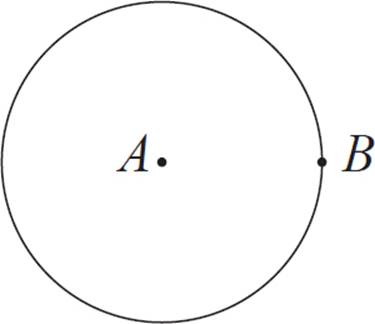
Position the compass so that the needle is on point B, and the drawing point is on A. With this radius, make two arcs that intersect the original circle. For the purposes of this exercise, label these intersection points C and G.

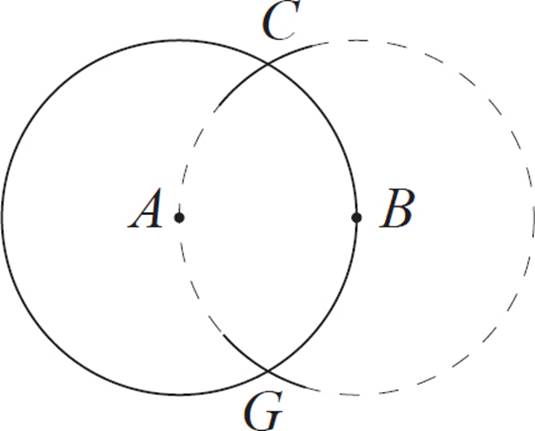
Next, position the compass so that the needle is on point C, and the drawing point is on A. With this radius, make an arc that intersects the original circle. Label this intersection point D.

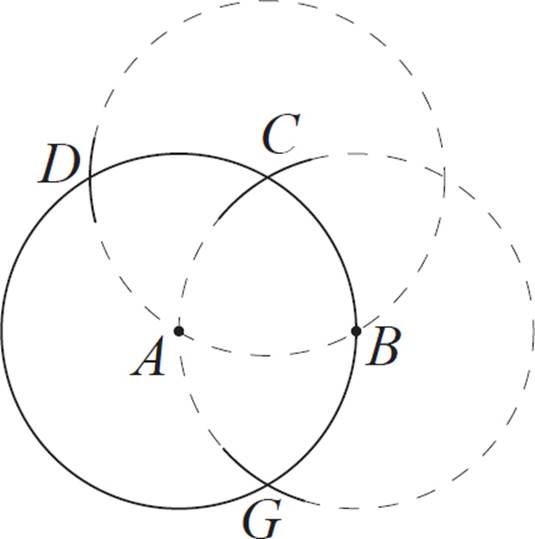
Next, position the compass so that the needle is on point D, and the drawing point is on A. With this radius, make an arc that intersects the original circle. Label this intersection point E.

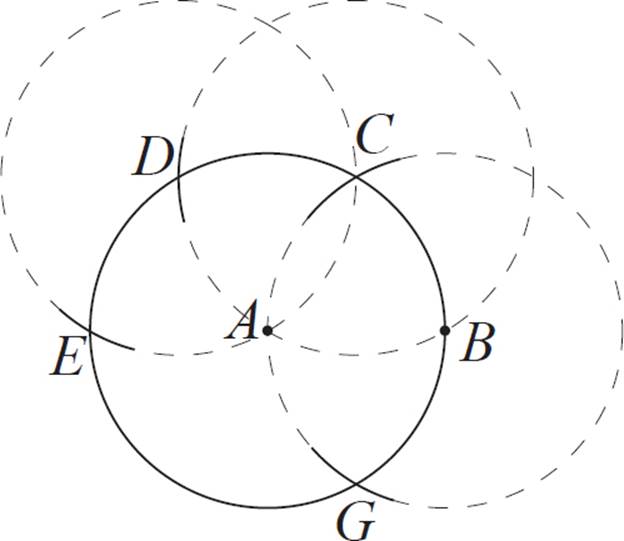
Next, position the compass so that the needle is on point E, and the drawing point is on A. With this radius, make an arc that intersects the original circle. Label this intersection point F.

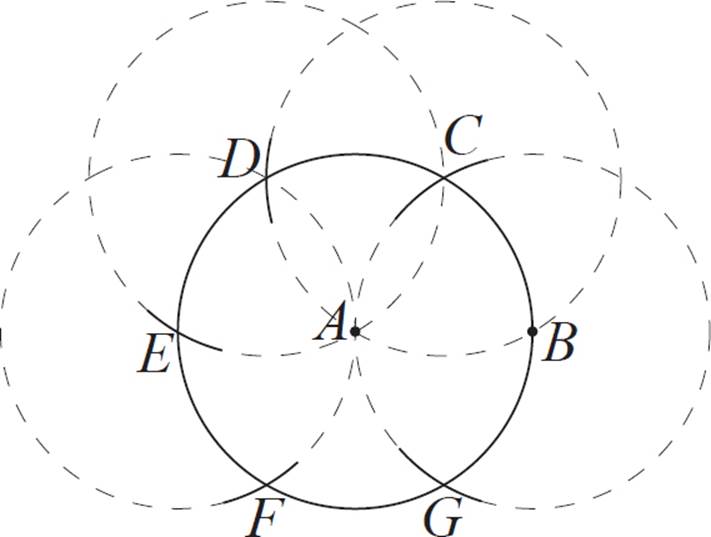
The final step is to connect points B, D, and F to make a triangle. (Alternatively, you could use points C, E, and G instead.)

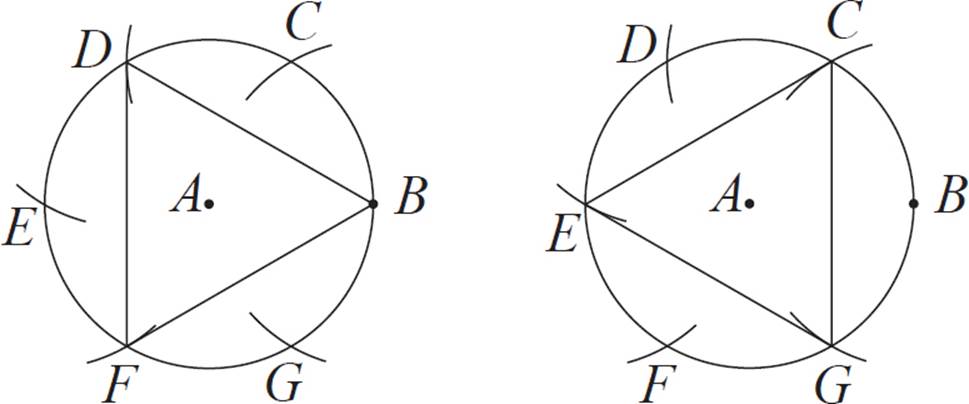
This triangle is equilateral, and it is inscribed in the circle. The reason this works is that we used the same compass radius for each arc we made—in other words, the intersection points were equally spaced from each other.

REGULAR HEXAGON

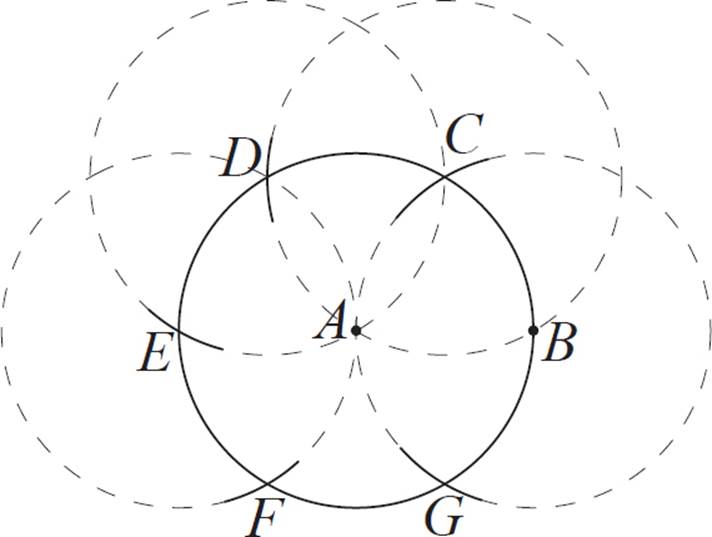
This method uses all the same steps as those used in the previous exercise (equilateral triangle inscribed in a circle). The difference is that at the end, you’ll connect all six intersection points instead of just three.

Follow the steps in the previous exercise (equilateral triangle inscribed in a circle), proceeding until you’ve drawn all six arcs on the circle. See the figure below.

The final step is to connect these six intersection points to form a hexagon, as in the figure below. Use your straightedge.

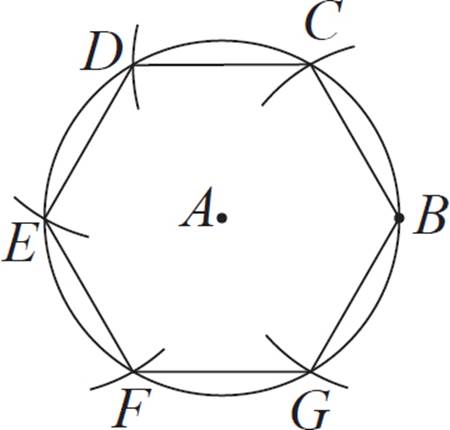
This hexagon is equilateral, and it is inscribed in the circle. The reason this works is that we used the same compass radius for each arc we made—in other words, the intersection points were equally spaced from each other.

SQUARE

Method 1—Start with Perpendicular Lines

In this exercise, you’ll use your compass and straightedge to construct a square. For this method, start by following the steps for constructing perpendicular lines, seen earlier in this chapter. You can use either of the methods recommended. It might be a good idea to erase the circles as best you can, leaving only the perpendicular lines.

Once you have perpendicular lines, proceed to the next step. Position your compass needle at the intersection point of the two lines, and make a circle. You can also just make arcs at the points where the circle crosses the two perpendicular lines.

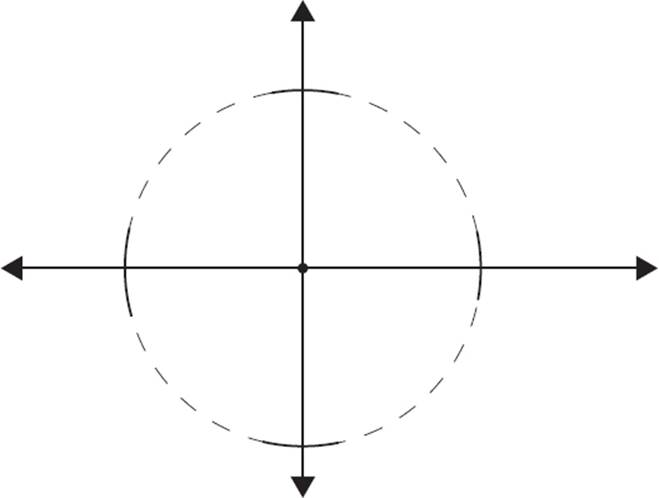
The circle crosses the two perpendicular lines, creating four intersection points. The next step is to connect those four intersection points to form a square, as in the figure below.

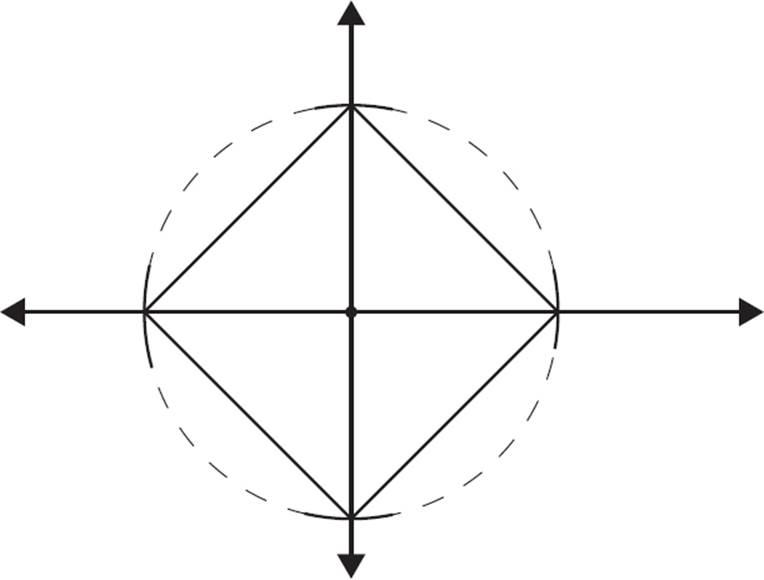
The quadrilateral drawn is a perfect square. One reason this works is that we know the two diagonals are perpendicular (we constructed them that way), and the four vertices are equidistant from the center.

Try a few more for practice! Follow the steps as above to create a square. Repeat until you’re comfortable with the process.

Method 2—Inscribed in a Circle

For this method, begin with a circle, with a point marked for its center.

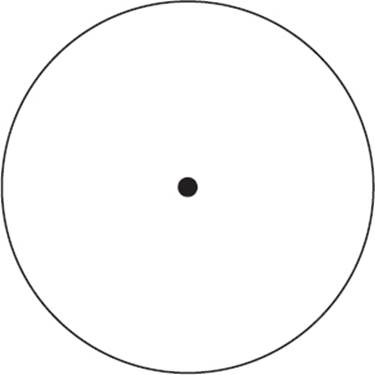
Position your straightedge carefully so that its line passes through the circle’s center. Draw a straight line, which will be the diameter of the circle, or just mark the points where the straightedge intersects the circle. Label these points Aand B.

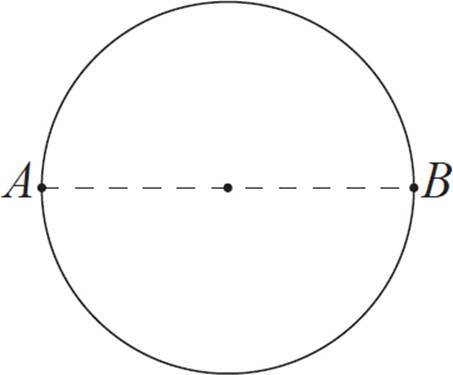
The next steps will be to construct a perpendicular bisector of this circle’s diameter. Position the compass so that the needle is on point A, and the drawing point is on B. Make a circle, which will be larger than the given circle. Or, just make two arcs, one above and one below the diameter, spanning the spots where the perpendicular bisector will go (eyeball it).

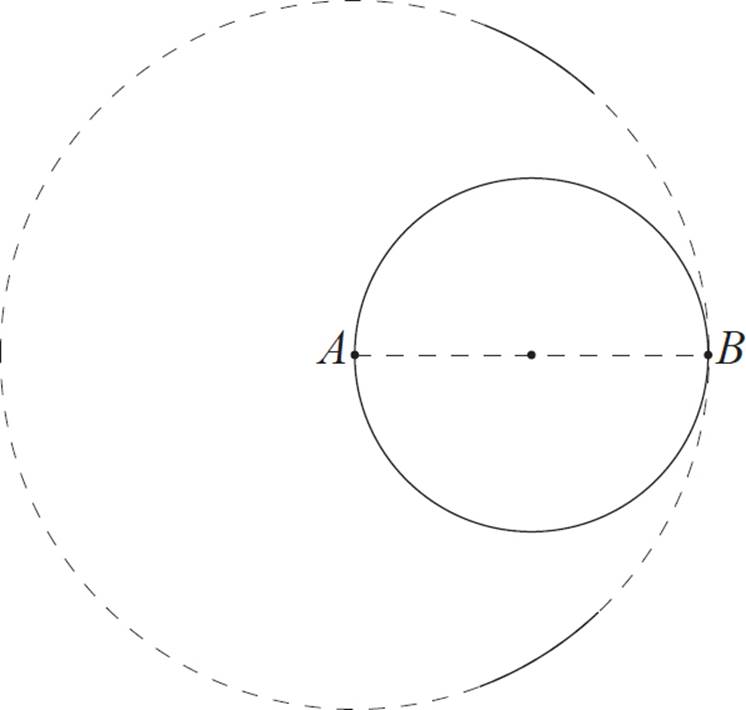
Next, position the compass so that the needle is on point B, and the drawing point is on A. Make a circle, or just two arcs, which intersect the previous arcs.

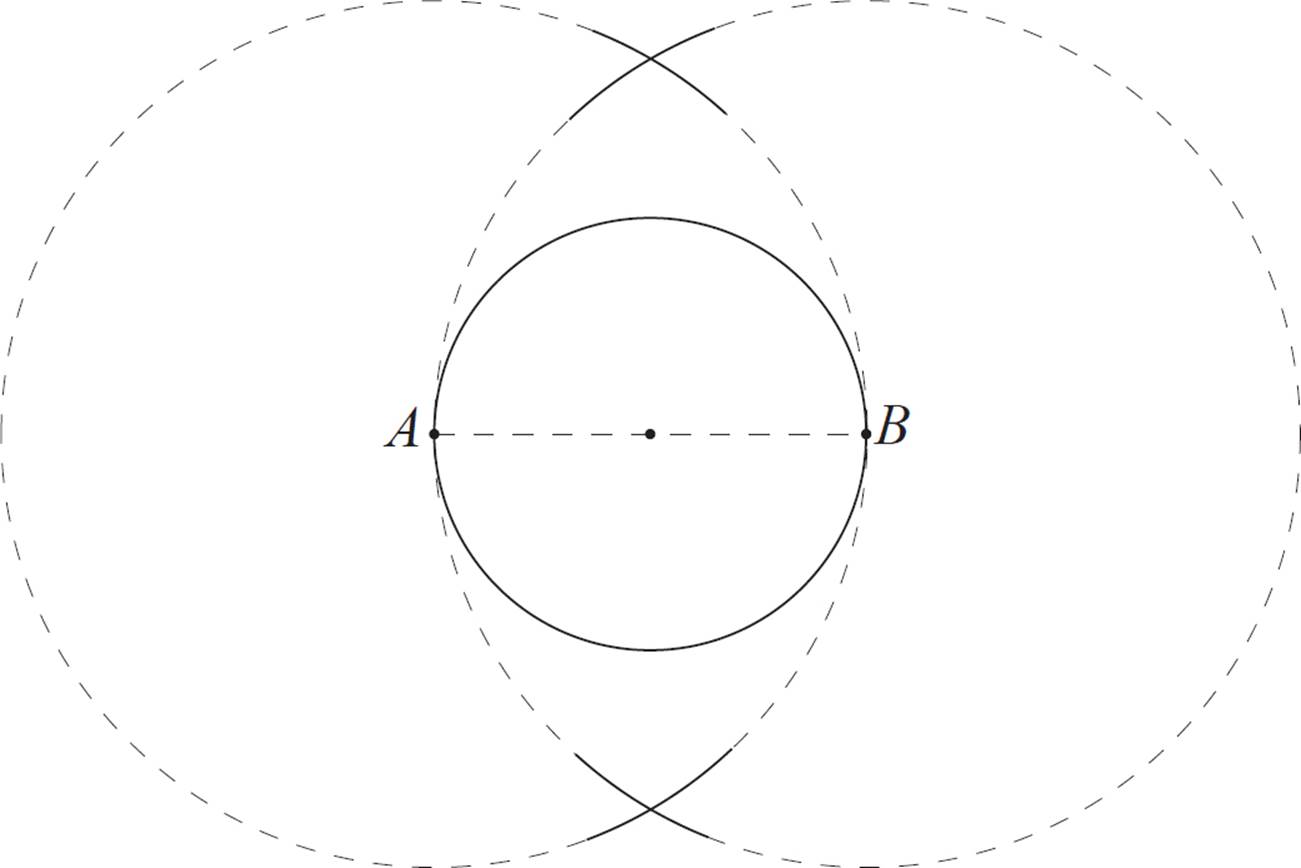
Position your straightedge to connect the two intersections of these larger arcs (it should also pass through the circle’s center). Draw a straight line, or just mark the points where the straightedge intersects the original circle. Label these points C and D.

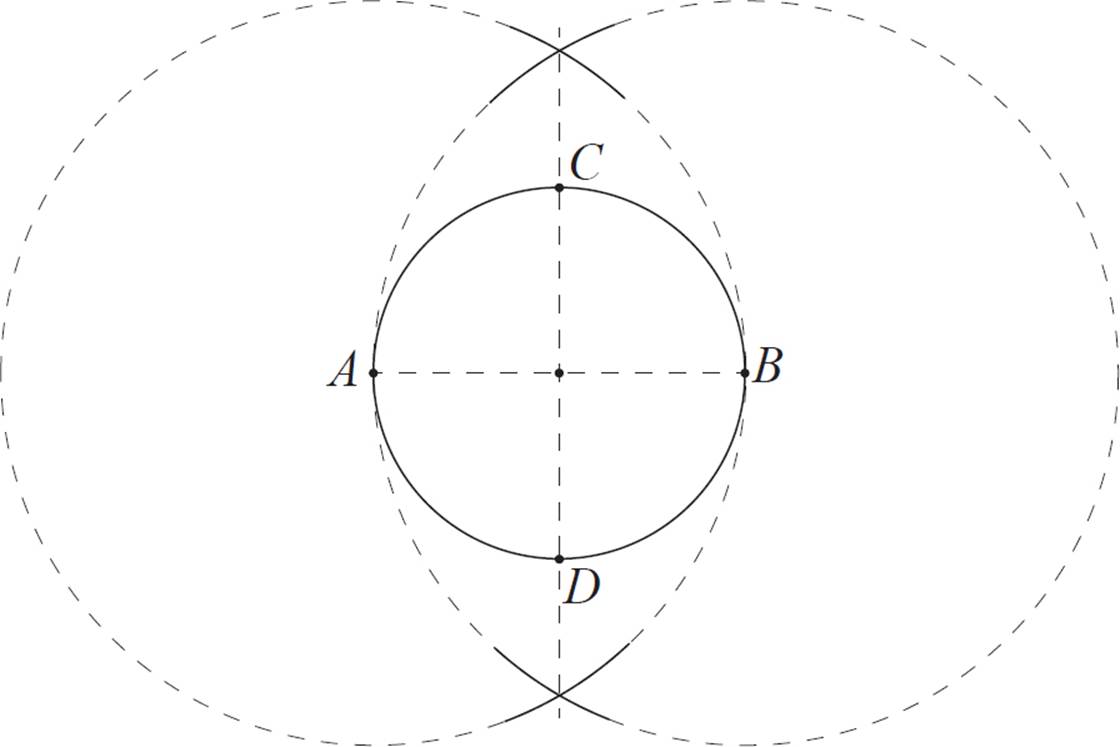
Finally, use your straightedge to connect points A, B, C, and D, forming a square.

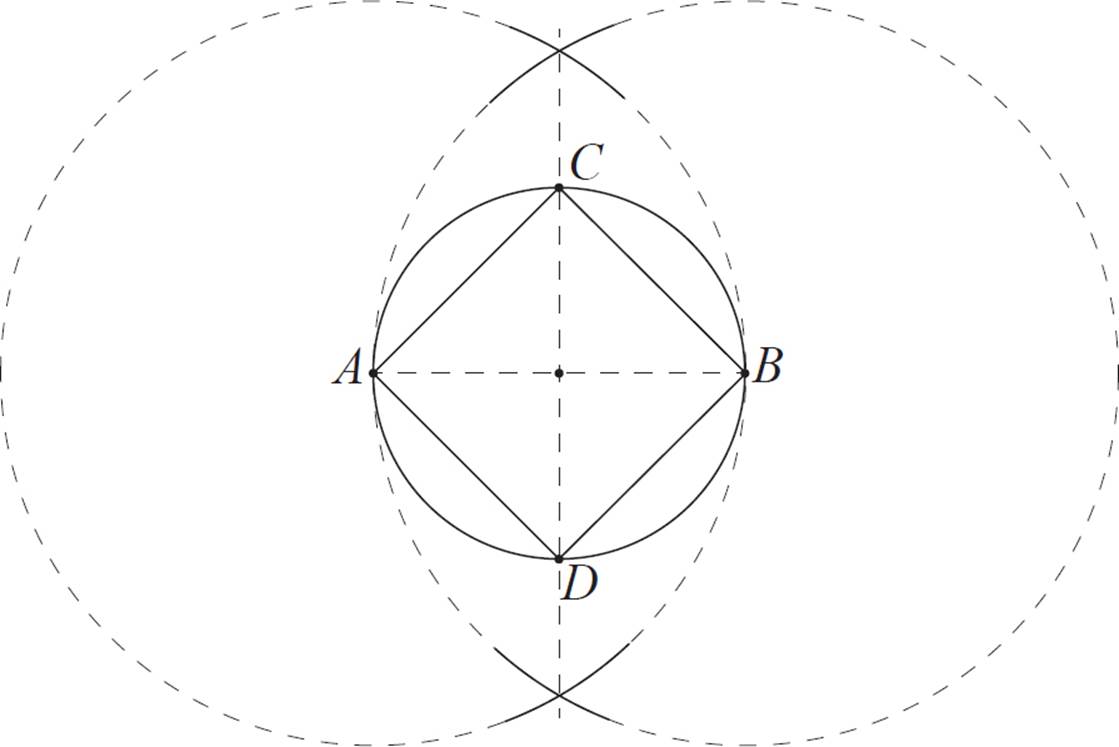
This square is inscribed in the circle.

Try a few more for practice! Follow the steps as above to create a square. Repeat until you’re comfortable with the process.

ANSWERS TO CHAPTER 2 EXERCISES

SSS Postulate Exercise

1.No.

These triangles have different lengths for all three sides; therefore, they are not congruent.

2.No.

These triangles have only one side length in common; therefore, they are not congruent.

3.No.

These triangles have two side lengths in common. However, the third side is not the same for both triangles. Therefore, they are not congruent.

4.Yes.

These triangles have the same lengths for all three sides; therefore, they are congruent.

5.Yes.

These triangles have the same lengths for all three sides; therefore, they are congruent.

6.No.

These triangles have two side lengths in common. However, one side length is unknown; therefore, they are not necessarily congruent.

AAS Postulate Exercise

1.No.

These triangles have different lengths for the given sides; therefore, they are not congruent.

2.Yes.

Use the ASA postulate—there is an angle, side, and angle (in that order) that are congruent in the two triangles. Therefore, they are congruent.

3.No.

These triangles have two angles in common. However, the given side is in a different place relative to the angles—in the first triangle, the given side is opposite the 30° angle, and in the second triangle, it’s opposite the 50° angle. Therefore, they are not congruent.

4.Yes.

Use the AAS postulate—there is an angle, angle, and side (in that order) that are congruent in the two triangles. Therefore, they are congruent.

5.No.

These triangles have one side and one angle in common. However, they do not follow either ASA or AAS congruence. Therefore, they are not necessarily congruent.

6.Yes.

Use the AAS postulate—there is an angle, angle, and side (in that order) that are congruent in the two triangles. Therefore, they are congruent.

DRILL

CHAPTER 2 PRACTICE QUESTIONS

Directions: Complete the following problems as specified by each question. For extra practice after answering each question, try using an alternative method to solve the problem or check your work. Larger, printable versions of images are available in your online student tools.

Click here to download a PDF of Chapter 2 Practice Questions.

1.Which of the following could represent the side lengths of a right triangle? (Select all that apply.)

□30, 60, 90

□15, 36, 39

□30, 40, 50

□16, 30, 34

□15, 21, 27

□14, 48, 51

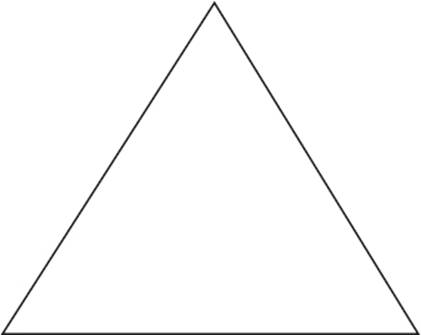
2.Using constructions, and not direct measurement, determine whether the triangle below is equilateral.

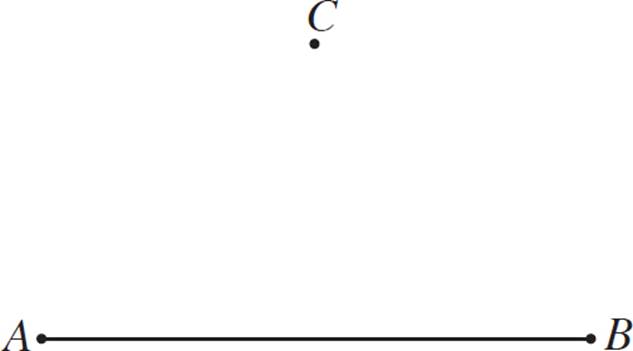
3.Using constructions, and not direct measurement, determine whether AC ≅ BC.

4.

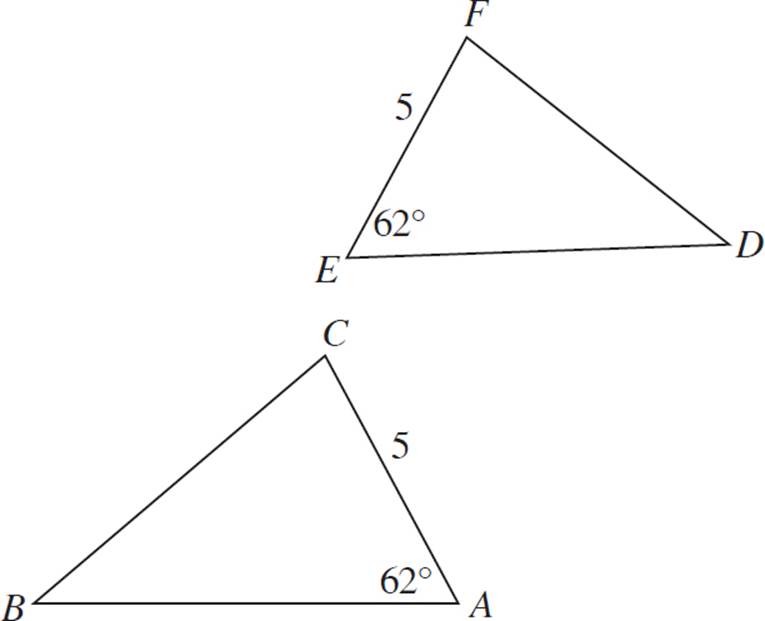
Which of the following facts alone, if true, would be sufficient to prove that triangles ABC and DEF are congruent? (Select all that apply.)

□AB ≅ ED

□AC ≅ FD

□CA ≅ ED

□∠ACB ≅ ∠DFE

□∠CBA ≅ ∠FDE

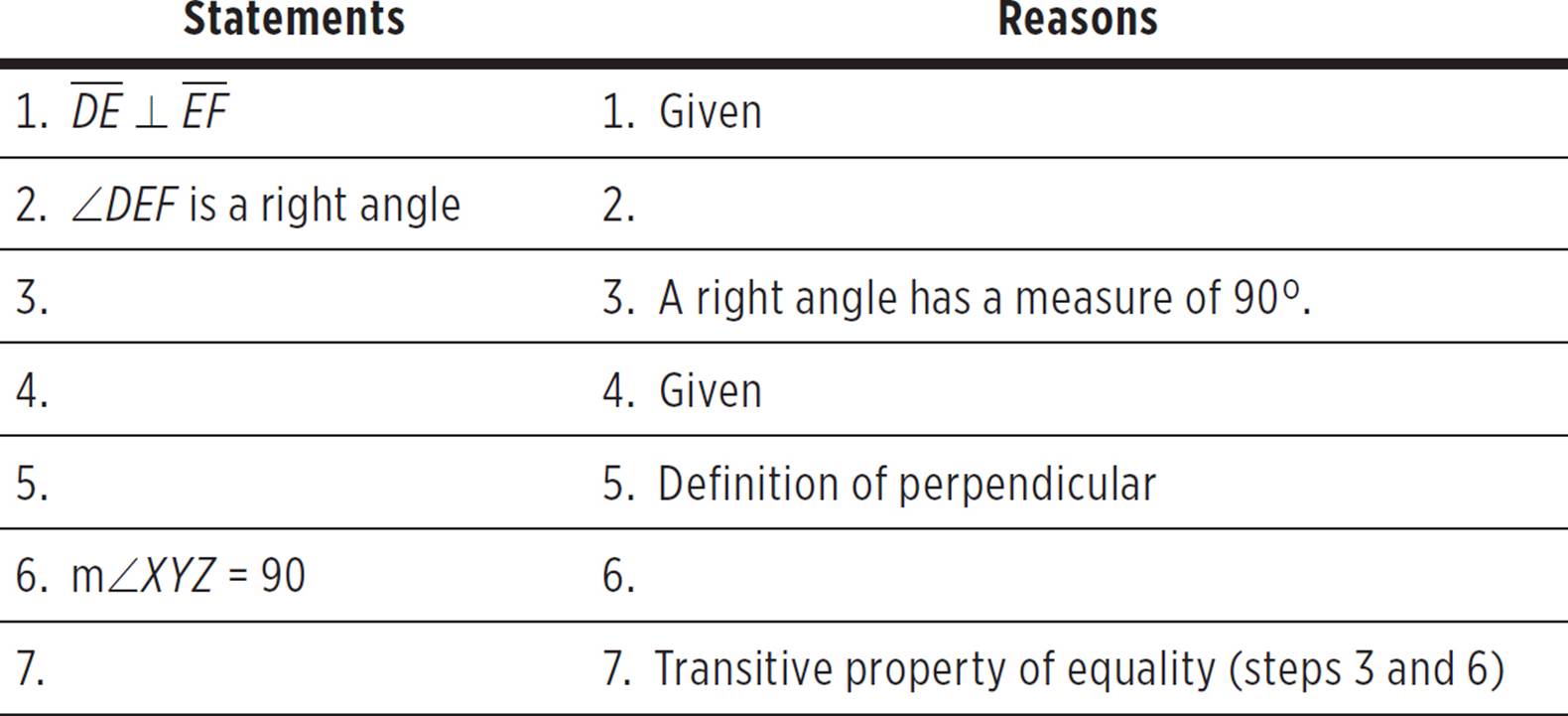
5.Given: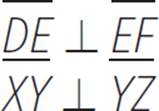

Prove: m∠DEF = m∠XYZ

Complete the following proof:

6.

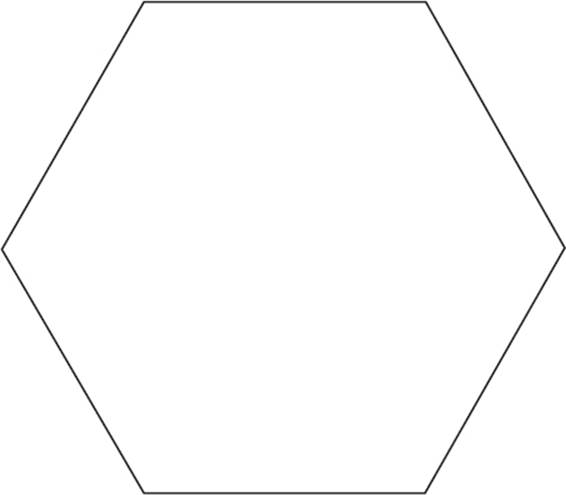
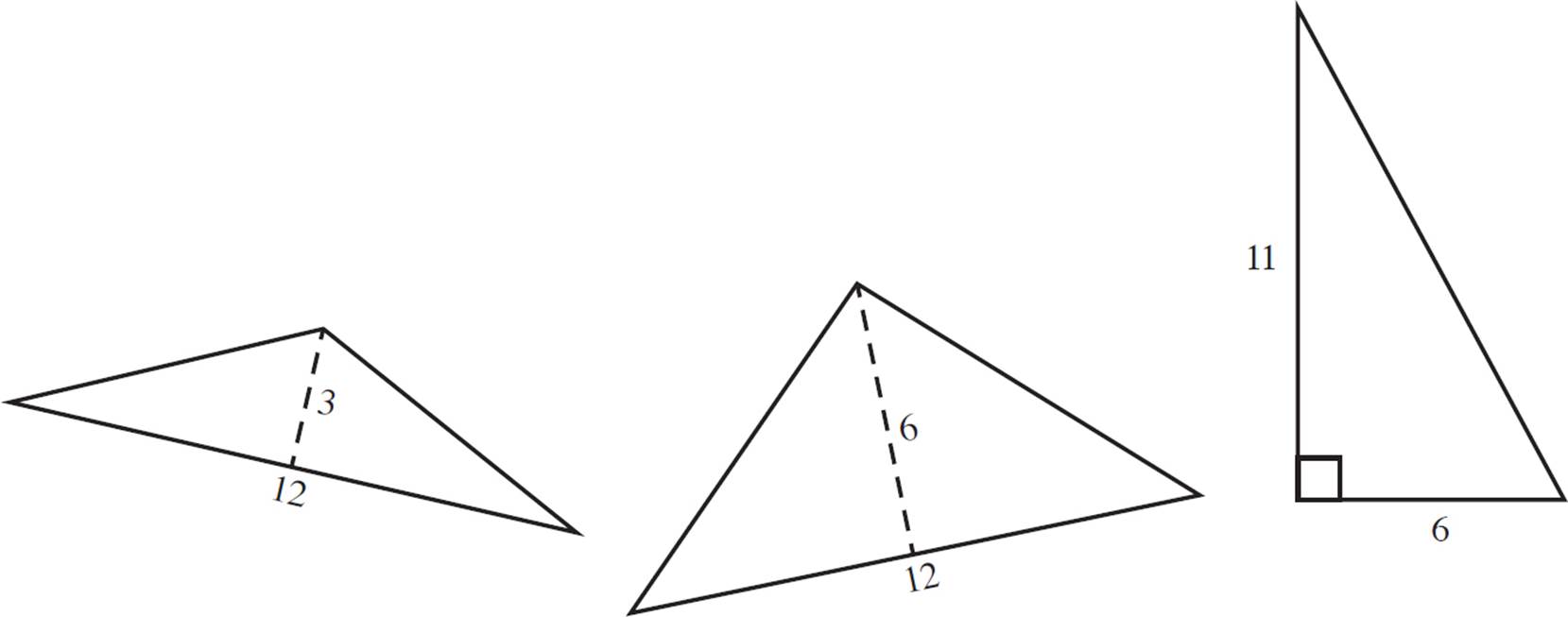
The figure above is a regular hexagon with side length 6. Which of the following triangles could fit inside the hexagon? (The triangle may be rotated, and it does not necessarily have to be inscribed).

7.A triangle has sides with lengths 14 and 6. Find:

a.the range of possible values for the third side

b.the range of possible values for the perimeter

8.

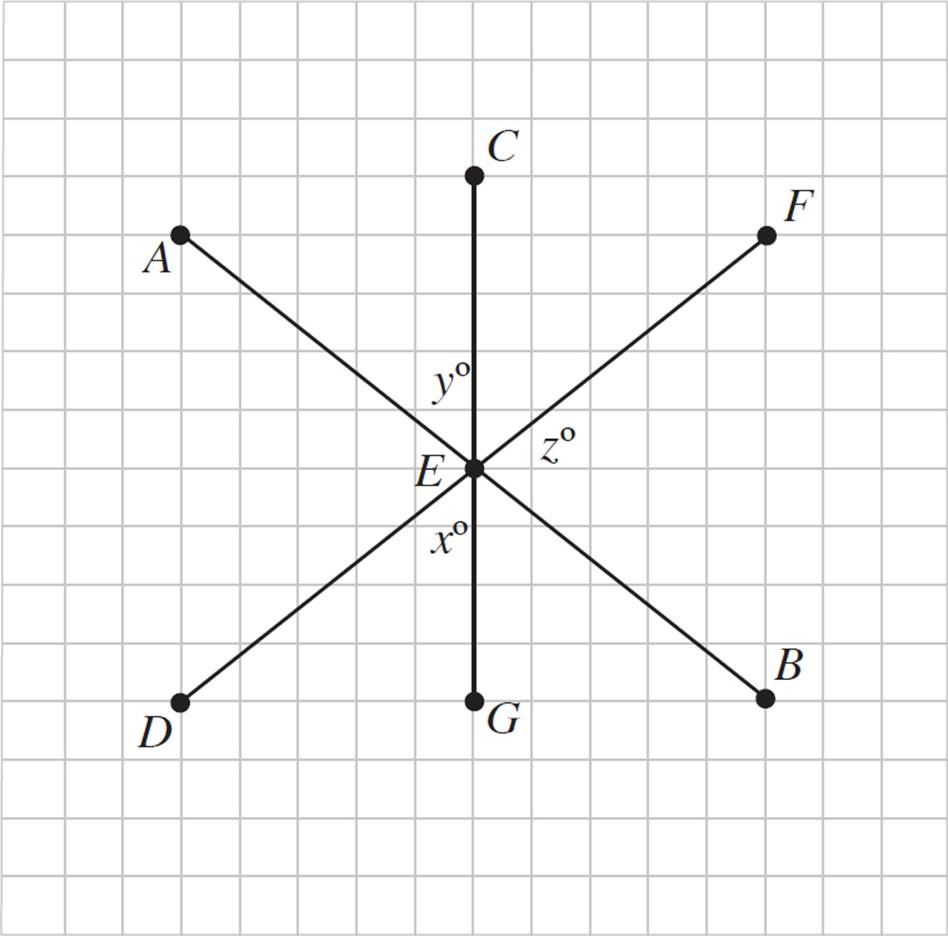
In the figure provided, EF bisects ∠CEB, DE bisects ∠AEG, and AB, CG, and DF all intersect at E.

a.If x = 50°, then find the value of all other angles.

b.Does 2(x + y + z) = 360°?

c.Is it always true that x = z?

d.Is it always true that y = x?

SOLUTIONS TO CHAPTER 2 PRACTICE QUESTIONS

1.(B), (C), and (D) are right triangles.

For each example, use Pythagorean theorem (a² + b² = c²) to determine whether the numbers could represent the side lengths of right triangles. Since there are no unknowns (variables) in these equations, you’re just trying to determine whether the equations are true.

Reminder: The longest side is always the hypotenuse, or c in the equation.

☒ 30² + 60² = 90²

900 + 3600 = 8100

4500 ≠ 8100

Pythagorean theorem with a = 30, b = 60, and c = 90
Simplify

✘ Not a true equation. This is not a right triangle.

✓ 15² + 36² = 39²

225 + 1296 = 1521

1521 = 1521

Pythagorean theorem with a = 15, b = 36, and c = 39
Simplify

✓ True equation. This is a right triangle.

Note: 15:36:39 is the third multiple of 5:12:13, a common Pythagorean triple.

✓ 30² + 40² = 50²

900 + 1600 = 2500

2500 = 2500

Pythagorean theorem with a = 30, b = 40, and c = 50
Simplify

✓ True equation. This is a right triangle.

Note: 30:40:50 is the tenth multiple of 3:4:5, a common Pythagorean triple.

✓ 16² + 30² = 34²

256 + 900 = 1156

1156 = 1156

Pythagorean theorem with a = 16, b = 30, and c = 34
Simplify

✓ True equation. This is a right triangle.

Note: 16:30:34 is the second multiple of 8:15:17, a common Pythagorean triple.

☒ 15² + 21² = 27²

225 + 441 = 729

666 ≠ 729

Pythagorean theorem with a = 15, b = 21, and c = 27
Simplify

✘ Not a true equation. This is not a right triangle.

☒ 14² + 48² = 51²

196 + 2304 = 2601

2500 ≠ 2601

Pythagorean theorem with a = 14, b = 48, and c = 51
Simplify

✘ Not a true equation. This is not a right triangle.

2.The triangle is equilateral.

In Lesson 2.4, the way we constructed an equilateral triangle was by using circles centered at two points, similar to constructing a perpendicular bisector. The third vertex was the intersection of these two circles.

You can use the same idea to determine whether a triangle is equilateral. Make two circles, each with radius AB, and centered at A and B, respectively. (Points are labeled here for the purposes of the explanation). Since C lies on the intersection point of the two circles, the triangle is equilateral.

Another way to think about this is that each of the three sides is equal to the radius of the circles. AB is the radius of both circle A and circle B, so we know that both circles are congruent. AC is the radius of circle A, and BC is the radius of circle B.

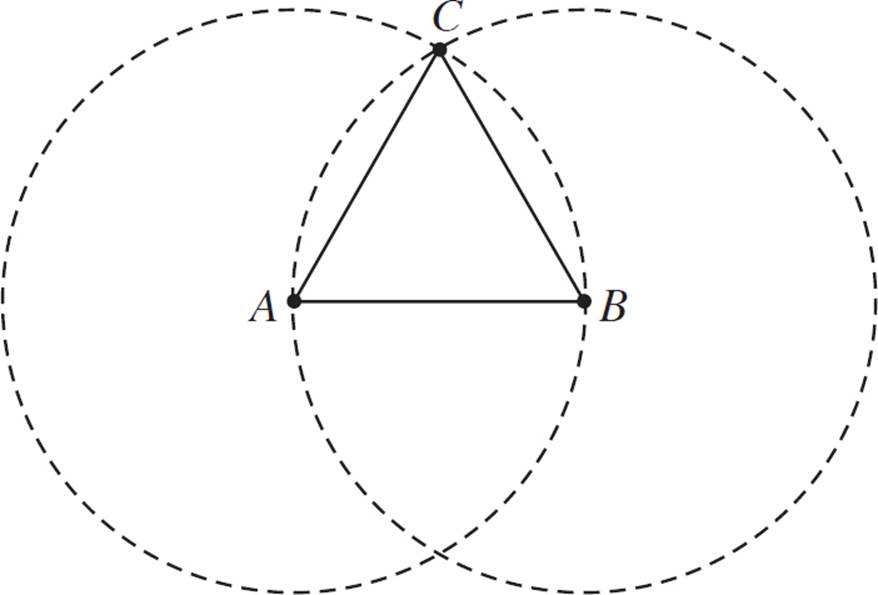
3.It is true that AC ≅ BC.

One efficient way to solve this problem is to construct a perpendicular bisector through segment AB. Since a bisector divides a line segment precisely in half, this will tell you whether AC ≅ BC.

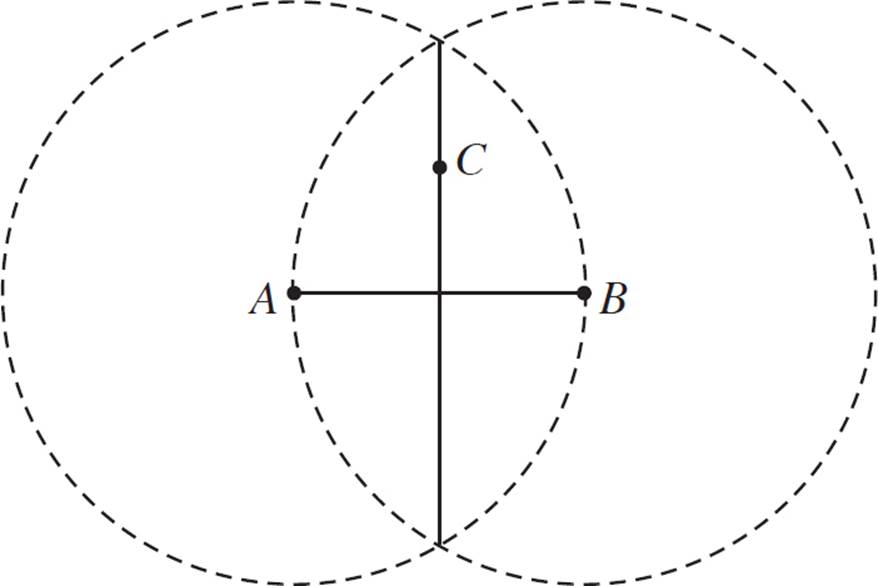
Construct the perpendicular bisector as shown above. Make two circles, each with radius AB, and centered at A and B, respectively. The intersection of these two circles is the perpendicular bisector. You should find that it passes through point C. Since AC lies on the perpendicular bisector, you know that AC ≅ BC.

Another explanation for this figure is in the form of right triangles. If you drew the segments connecting AC and BC, you would have two congruent right triangles. You know that they are congruent, because segment AB is bisected, and the other segment through point C is shared between both triangles, so that segment is congruent to itself. That means that the hypotenuses of these triangles must be congruent as well.

4.✓ AB ≅ ED

☒ AC ≅ FD

☒ CA ≅ ED

✓ ∠ACB ≅ ∠DFE

✓ ∠CBA ≅ ∠FDE

AB ≅ ED would prove congruence through SAS.

AC ≅ FD would not be sufficient to prove congruence, because SSA is not a congruence property. Actually, if you knew that both of these triangles are acute (as they appear to be), then SSA can work (since it rules out one of the two possible triangles that can be made from that information). These triangles appear to be acute, but you should not assume that figures are drawn to scale unless they are specifically described as such. So based on the given information alone, you should conclude that the triangles can’t be proved congruent.

CA ≅ ED would not be sufficient to prove congruence, because the segments do not correspond. (CA is opposite the given angle, while ED is adjacent to the given angle).

∠ACB ≅ ∠DFE would prove congruence through ASA.

∠CBA ≅ ∠FDE would prove congruence through AAS.

5. Your proof should look like the one below. It’s fine if you have some slight differences that are equivalent in meaning.

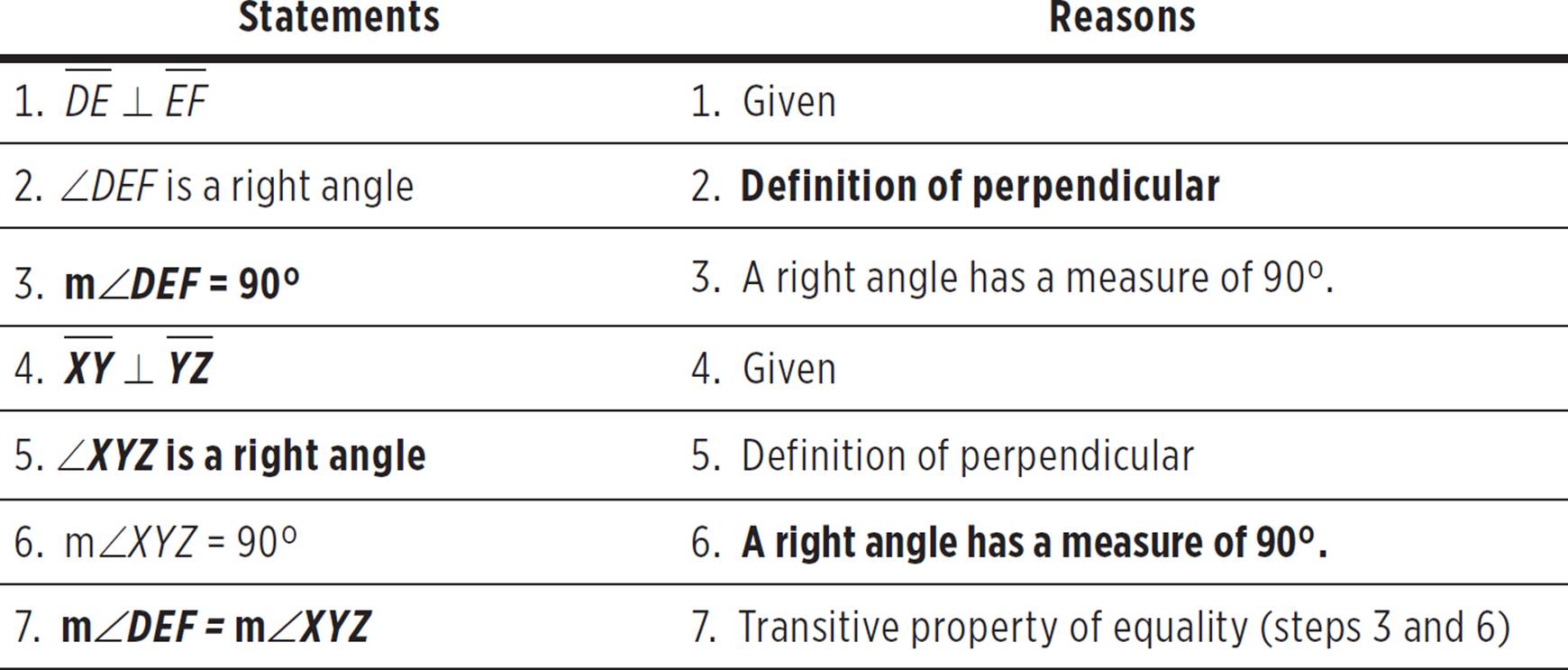
For Statement 2, we’re saying that ∠DEF is a right angle. How do you know that it is a right angle? Because you know that the segments are described as perpendicular (Statement 1), and you know that means that the segments intersect at a right angle. Thus, the reason is the definition of perpendicular. You may have also cited the actual definition, i.e. “Perpendicular segments intersect at right angles.”

For Statement 3, choose a statement that is related to the previous statements and/or given information, and is proved with the reason “a right angle has a measure of 90°.” The relevant statement here is that m∠DEF = 90°. This may have seemed like an overly obvious statement to make; but remember, for strict formal proofs, it’s necessary to include reasoning for every step in your logic.

For Statement 4, we know that we need a “given” statement, since that is the reason that is cited. The other “given” statement is that XY ⊥ YZ. Note that this also flows nicely with the logic of the proof, since the next statements are about m∠XYZ.

Statements 5 and 6 use the same logic as statements 2 and 3. You can prove that ∠XYZ is a right angle based on the “definition of perpendicular.” Then, prove that m∠XYZ = 90° based on the fact that a right angle has a measure of 90°. For Statement 6, you could have perhaps written “definition of right angle,” rather than citing the definition itself.

The final statement should always be the PROVE statement. In this case, you were trying to prove that m∠DEF = m∠XYZ. Also, you should verify that this statement is proved with the transitive property of equality. The transitive property states that, if you know that different things have the same value, then you know those things are equal to each other. This is a relevant property to use for the final statement, since you have proved that both ∠DEF and∠XYZ are equal to 90°.

6.

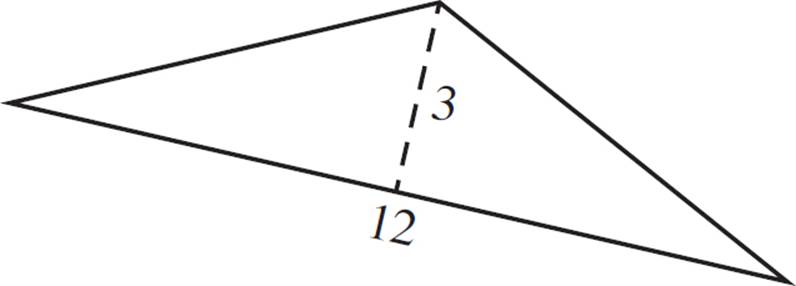
Of the triangles listed, only the first one would fit inside the hexagon.

Consider what you know about the hexagon. The longest diagonal must have a length of 12. (You can think of a hexagon as six smaller equilateral triangles that fit together—in this case, the smaller triangles would have a side length of 6, and two of them side-by-side would have a length of 12.)

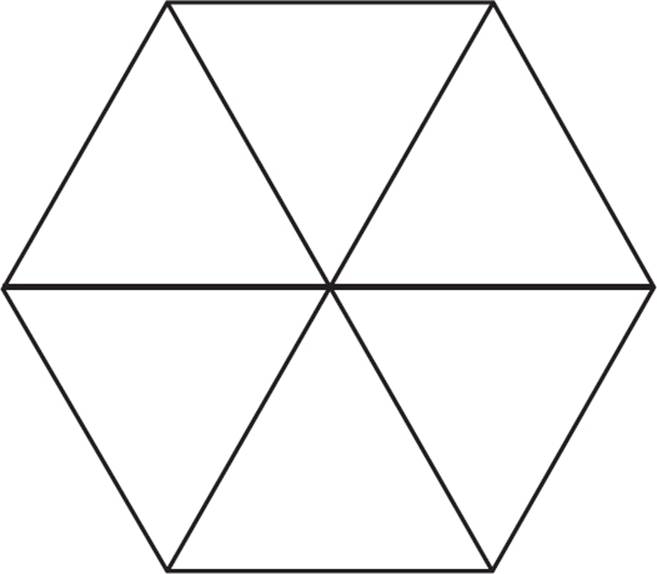
That means that a triangle with a base of 12 can fit in the width of the hexagon. But, how tall can that triangle be? Each smaller equilateral triangle would have a base of 6, and a height of 3. You can use the Pythagorean theorem to find this (a² + b² = c², 3² +b² = 6², solve for b.) The value of 3 is approximately 5.2. Therefore, the first triangle would fit inside the hexagon, but the second would not.

Similarly, if you have a right triangle with a base of 6 (as in the third triangle shown in the question), that would fit along the base of the hexagon, but how tall can it be? In the previous steps, you found that half the altitude of the hexagon is equal to 3. Double that to find the altitude: 6, or approximately 10.4. This is smaller than 11; therefore, the third triangle would not fit in the hexagon, either.

7. a.The third side can have any length between 8 and 20.

b.The perimeter can have any length between 28 and 40.

Recall the Third Side Rule: In any triangle, the length of one side must be greater than the difference and less than the sum of the other two sides.

To find the range for the third side, find the sum and the difference of the two given values, 14 and 6. The sum is 14 + 6 = 20. The difference is 14 − 6 = 8. Therefore, the range of values for the third side is 8 < x < 20.

To find the range for the perimeter, use the values you found for the third side. The third side must be greater than 8, so the perimeter must be greater than 28 (= 8 + 14 + 6). The third side must be less than 20, so the perimeter must be less than 40 (= 20 + 14 + 6).

8. a.Through vertical angle congruency, we know that ∠AEC ≅ ∠GEB ∠CEF ≅ ∠DEG, and ∠FEB ≅ ∠AED. Next, if x = 50, then ∠ DEG = ∠ CEF = 50°. Additionally, EF bisects ∠CEB (given), so we know that ∠CEF ≅ ∠FEB. Therefore, ∠CEF = ∠FEB = ∠AED = 50°. Finally, you can prove that ∠AEC = ∠GEB = 80°, because 80°+ 50° + 50° = 180° (use adjacent angles forming a straight line).

b.Since ∠AEC ≅ ∠GEB, x + y + z = 180, and 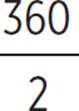= 180; then, through the transitive property, x + y + z = 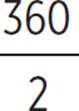, and 2(x + y + z) = 360. Therefore, yes, 2(x + y + z) = 360°.

c.Through vertical angle congruency, ∠DEG ≅ ∠CEF. Since EF bisects ∠CEB, it is always true that x = z.

d.∠AEC ≅ ∠GEB through vertical angle congruency and ∠AED ≅ ∠ DEG ≅ ∠CEF ≅ ∠BEF for bisector properties and vertical angle congruency. Since there is no equation of angles for y and x, they are not ever equal to one another. Therefore, y ≠ x.

REFLECT

Congratulations on completing Chapter 2!

Here’s what we just covered.

Rate your confidence in your ability to:

•Identify congruent triangles using the SSS, AAS, ASA, SAS postulates

•Use the Pythagorean theorem or the Third Side Rule to solve for an unknown side in a right triangle

•Understand how to write a formal or informal proof

•Construct figures with a compass and straightedge (parallel and perpendicular lines, angle bisector, angle copy, equilateral triangle, square, and regular hexagon)

If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.

Access your online student tools for a handy, printable list of Key Points for this chapter. These can be helpful for retaining what you’ve learned as you continue to explore these topics.