GMAT Quantitative Review

3.0 Math Review

Although this chapter provides a review of some of the mathematical concepts of arithmetic, algebra, and geometry, it is not intended to be a textbook. You should use this chapter to familiarize yourself with the kinds of topics that may be tested in the GMAT® exam. You may wish to consult an arithmetic, algebra, or geometry book for a more detailed discussion of some of the topics.

Section 3.1, “Arithmetic,” includes the following topics:

1. Properties of Integers

2. Fractions

3. Decimals

4. Real Numbers

5. Ratio and Proportion

6. Percents

7. Powers and Roots of Numbers

8. Descriptive Statistics

9. Sets

10.Counting Methods

11.Discrete Probability

Section 3.2, “Algebra,” does not extend beyond what is usually covered in a first-year high school algebra course. The topics included are as follows:

1. Simplifying Algebraic Expressions

2. Equations

3. Solving Linear Equations with One Unknown

4. Solving Two Linear Equations with Two Unknowns

5. Solving Equations by Factoring

6. Solving Quadratic Equations

7. Exponents

8. Inequalities

9. Absolute Value

10.Functions

Section 3.3, “Geometry,” is limited primarily to measurement and intuitive geometry or spatial visualization. Extensive knowledge of theorems and the ability to construct proofs, skills that are usually developed in a formal geometry course, are not tested. The topics included in this section are the following:

1. Lines

2. Intersecting Lines and Angles

3. Perpendicular Lines

4. Parallel Lines

5. Polygons (Convex)

6. Triangles

7. Quadrilaterals

8. Circles

9. Rectangular Solids and Cylinders

10.Coordinate Geometry

Section 3.4, “Word Problems,” presents examples of and solutions to the following types of word problems:

1. Rate Problems

2. Work Problems

3. Mixture Problems

4. Interest Problems

5. Discount

6. Profit

7. Sets

8. Geometry Problems

9. Measurement Problems

10.Data Interpretation

3.1 Arithmetic

1. Properties of Integers

An integer is any number in the set {. . . −3, −2, −1, 0, 1, 2, 3, . . .}. If x and y are integers and , then x is a divisor (factor) of y provided that for some integer n. In this case, y is also said to be divisible by x or to be a multiple of x. For example, 7 is a divisor or factor of 28 since , but 8 is not a divisor of 28 since there is no integer n such that 28 = 8n.

If x and y are positive integers, there exist unique integers q and r, called the quotient and remainder, respectively, such that and . For example, when 28 is divided by 8, the quotient is 3 and the remainder is 4 since . Note that y is divisible by x if and only if the remainder r is 0; for example, 32 has a remainder of 0 when divided by 8 because 32 is divisible by 8. Also, note that when a smaller integer is divided by a larger integer, the quotient is 0 and the remainder is the smaller integer. For example, 5 divided by 7 has the quotient 0 and the remainder 5 since .

Any integer that is divisible by 2 is an even integer; the set of even integers is {. . . −4, −2, 0, 2, 4, 6, 8, . . .}. Integers that are not divisible by 2 are odd integers; {. . . −3, −1, 1, 3, 5, . . .} is the set of odd integers.

If at least one factor of a product of integers is even, then the product is even; otherwise the product is odd. If two integers are both even or both odd, then their sum and their difference are even. Otherwise, their sum and their difference are odd.

A prime number is a positive integer that has exactly two different positive divisors, 1 and itself. For example, 2, 3, 5, 7, 11, and 13 are prime numbers, but 15 is not, since 15 has four different positive divisors, 1, 3, 5, and 15. The number 1 is not a prime number since it has only one positive divisor. Every integer greater than 1 either is prime or can be uniquely expressed as a product of prime factors. For example, , , and .

The numbers −2, −1, 0, 1, 2, 3, 4, 5 are consecutive integers. Consecutive integers can be represented by n, n + 1, n + 2, n + 3, . . . , where n is an integer. The numbers 0, 2, 4, 6, 8 are consecutive even integers, and 1, 3, 5, 7, 9 are consecutive odd integers. Consecutive even integers can be represented by 2n, , , . . . , and consecutive odd integers can be represented by , , , . . . , where n is an integer.

Properties of the integer 1. If n is any number, then , and for any number , .

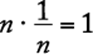The number 1 can be expressed in many ways; for example, for any number .

Multiplying or dividing an expression by 1, in any form, does not change the value of that expression.

Properties of the integer 0. The integer 0 is neither positive nor negative. If n is any number, then and . Division by 0 is not defined.