GMAT Quantitative Review

3.0 Math Review

3.1 Arithmetic

2. Fractions

In a fraction , n is the numerator and d is the denominator. The denominator of a fraction can never be 0, because division by 0 is not defined.

Two fractions are said to be equivalent if they represent the same number. For example, and are equivalent since they both represent the number . In each case, the fraction is reduced to lowest terms by dividing both numerator and denominator by theirgreatest common divisor (gcd). The gcd of 8 and 36 is 4 and the gcd of 14 and 63 is 7.

Addition and subtraction of fractions.

Two fractions with the same denominator can be added or subtracted by performing the required operation with the numerators, leaving the denominators the same. For example, 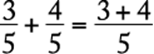and 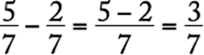. If two fractions do not have the same denominator, express them as equivalent fractions with the same denominator. For example, to add and , multiply the numerator and denominator of the first fraction by 7 and the numerator and denominator of the second fraction by 5, obtaining and , respectively; .

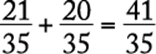For the new denominator, choosing the least common multiple (lcm) of the denominators usually lessens the work. For 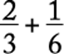, the lcm of 3 and 6 is 6 (not ), so .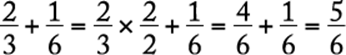

Multiplication and division of fractions.

To multiply two fractions, simply multiply the two numerators and multiply the two denominators.

For example, .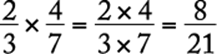

To divide by a fraction, invert the divisor (that is, find its reciprocal) and multiply. For example, .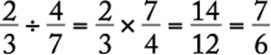

In the problem above, the reciprocal of is . In general, the reciprocal of a fraction is , where n and d are not zero.

Mixed numbers.

A number that consists of a whole number and a fraction, for example, , is a mixed number:

means .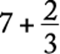

To change a mixed number into a fraction, multiply the whole number by the denominator of the fraction and add this number to the numerator of the fraction; then put the result over the denominator of the fraction. For example, 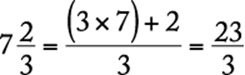.