GMAT Quantitative Review
3.0 Math Review
3.1 Arithmetic
7. Powers and Roots of Numbers
When a number k is to be used n times as a factor in a product, it can be expressed as kn, which means the nth power of k. For example, 
and 
are powers of 2.
Squaring a number that is greater than 1, or raising it to a higher power, results in a larger number; squaring a number between 0 and 1 results in a smaller number. For example:
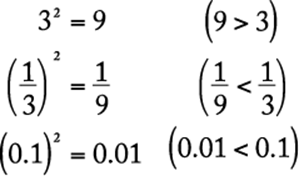
A square root of a number n is a number that, when squared, is equal to n. The square root of a negative number is not a real number. Every positive number n has two square roots, one positive and the other negative, but 
denotes the positive number whose square is n. For example, 
denotes 3. The two square roots of 9 are 
and 
.
Every real number r has exactly one real cube root, which is the number s such that 
. The real cube root of r is denoted by 
. Since 
, 
. Similarly, 
, because 
.