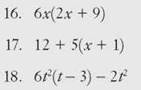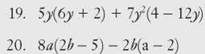Basic Math and Pre-Algebra
PART 2. Into the Unknown
CHAPTER 9. Adding and Subtracting with Variables
Simplifying Expressions
Once you have terms, it’s natural to want to start doing things with them. You can add or subtract terms if they’re like terms, and you can multiply terms by other terms, like or not. You can even do both of these things, adding and then multiplying. When you start doing so many things with terms, you soon need to stop and think about how you simplify the problems you’ve created.
Do you need a whole new set of rules? The good news is no. Your old friend PEMDAS (Parentheses, Exponents, Multiply, Divide, Add, Subtract) will cover most situations. Let’s look at a problem that’s not too complicated. Suppose you wanted to do 5x(3x + 7x). PEMDAS says do what’s in the parentheses first, so look at the 3x + 7x part first. Those are like terms, so you can add them and get 10x. Your expression 5x(3x + 7x) becomes 5x(10x). Exponents are next, but there are none, so move on to multiplying and dividing. 5x(10x) = 5 ∙ 10 ∙ x ∙ x = 50x2.
How about this one? Simplify -4xy(6x + 7y) using the same rules. Parentheses first. But this time, you can’t add what’s in the parentheses because they’re unlike terms. Don’t panic. You can only do what you can do, so just move on. There are no exponents, so it’s time to multiply, and for that, you’ll need the distributive property.
![]()
Now, as you look at each multiplication, multiply coefficients and combine what you can. Don’t be afraid to rearrange. Remember multiplication is commutative and associative.
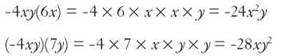
Put the pieces back together to get
![]()
Because you have the plus from the addition problem followed immediately by the minus sign from the -28, you can write your answer as -24x2y - 28xy2.
Your basic rules are:
• Combine what’s in the parentheses if you can.
• Distribute multiplication over the addition or subtraction if you can’t combine the unlike terms.
• Simplify each multiplication.
• Check the signs.
Whenever you have negatives in problems like these, it’s important to be careful about the rules for signs. If the multiplier that you’re distributing is positive, the signs aren’t usually a problem. Terms in the parentheses that were positive will produce positive terms in the answer, and terms that were negative in the parentheses will produce negative terms in the answer. Here are some examples.
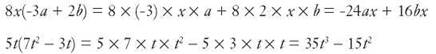
When the multiplier is negative, however, you need to work carefully and remember that if you distribute a negative term, the signs of each term in the parentheses will change. Let’s take those two examples and make the multipliers negative to see what happens.
Take the first example and change 8x to -8x. Distribute the -8x.
![]()
Now that first term has a negative multiplied by a negative, so the result is going to be positive. The second term has one negative, so that result will be negative.
![]()
You can eliminate the plus signs, condensing to 24ax - 16x.
If you change 5tto -5t in the second example and distribute, you get -5t(7t2 - 3t) = -5 ∙ 7 ∙ t ∙ t1 - (-5) ∙ 3 ∙ t ∙ t.
The first term will come out negative, but the second term is where you have to be careful. The product (-5) ∙ 3 ∙ t ∙ t will give you a negative result, -15t2, but you also have a minus in front of that, the one that was connecting the original terms. You get a product of -35t3 — -15t2, but the double minus becomes a plus so you end up with -35t3 + 15t2. The minus on the multiplier switches the signs.
Sometimes you’ll find an expression with more than one set of parentheses and lots of terms, some like and some unlike, and some that start out unlike and then turn into like terms. You just need to take things step by step and pay attention to what is happening. Here’s an example.
![]()
There are no like terms in the first parentheses, so you can’t do anything there, and no like terms in the second set of parentheses, either. Move on to multiplying. Use the distributive property.
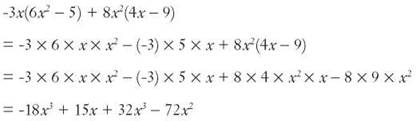
Now notice you have like terms: -18x3 and 32x3. You can combine those to get a final answer of 14x3 + 15x -72x2. It’s traditional to put your terms in order from highest exponent to lowest, so rewrite it as 14x3 - 72x2 + 15x.
CHECK POINT
Simplify each expression.