Basic Math and Pre-Algebra
PART 2. Into the Unknown
CHAPTER 9. Adding and Subtracting with Variables
Polynomials
There’s a particular group of expressions, which you’ll hear about in algebra, that are called polynomials. The prefix poly means “many,” so it would seem that they would be expressions with many terms, and some of them are. But the name polynomial is applied to any expression that fits a particular pattern, even those with only one term.
The pattern is easier to show than to describe, but let’s try. Polynomials are expressions that are made by adding terms that are the product of a numerical coefficient and a power of a certain variable. For example, 8x5, -6x3, x2, and 2x are all terms that are the product of a numerical coefficient and a power of the variable x. You don’t see the numerical coefficient in x2 because it’s 1, and we don’t usually show that. Constants can also be part of a polynomial because we can say a constant, like 3, is 3x0.
Each of these terms could be called a polynomial all by itself. It would be a one-term polynomial, also called a monomial. Mono is the prefix that means “one.” You can add monomials with the same variable to make a more complex polynomial. For example, 8x5 + -6x3 + x2 + 2x + 3 is a polynomial. If you add two monomials, like 5y3 + 2y, you make a binomial. If you add three monomials, like t2+ 3t + 1, that’s a trinomial. Monomials, binomials, and trinomials are all types of polynomials.
The degree of a monomial is the exponent on the variable. 8x5 is fifth degree, x2 is second degree, and 2x is first degree. You don’t see an exponent of 1, but that’s what 2x really means: 2x1. Constants are degree zero, because we’re thinking of them as a constant times x0.
MATH TRAP
Be careful to look at all the terms of a polynomial before you decide on its degree. Don't just jump at the term that happens to be written first.
The degree of a polynomial is the highest degree of all its monomials. The polynomial 8x5 + -6x3 + x2 + 2x + 3 is a fifth degree polynomial, and t2 - 7t + 4 is a second degree polynomial. For the polynomial 5t3 - 7t + 8t4 - 2t2 + 5, you need to be careful to look at the whole polynomial. The degree of the polynomial is 4, not 3. The highest degree term is in the middle, not the beginning, of the polynomial.
If there is more than one variable in a term, the degree of the term is the sum of the degrees of each variable. The term xy is degree 2, one for x and one for y. The term 3x4y2 is degree 6.
CHECK POINT
Give the degree of each polynomial.
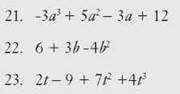
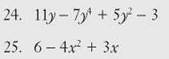
When you write a polynomial, no matter how many terms it has, it’s traditional to write it in standard form. Standard form means that you write the terms of the polynomial in order from the highest degree monomial to the lowest. The polynomial 8x5 + -6x3 + x2 + 2x + 3 is in standard form because the monomials start with the fifth degree, then the third degree, then the second, first, and finally the zero degree term.
WORLDLY WISDOM
The standard form of a polynomial writes the terms in order from highest degree to the lowest.
The polynomial 4t3 - 6t9 + 11t - 5t2 + 8t7 is not in standard form. To put it in standard form, you need to first locate the highest degree term. In this case, that’s -6t9. That has to be first, so move it around to the front. The 4t3 that was in front is positive, so you can put a plus between the ninth degree term and the 4t3 - 6t9 + 4t3 + 11t - 5t2 + 8t7.
There’s no eighth degree term, but there’s a seventh degree, so that should be next. -6t9 + 8t7+ 4t3 + 11t - 5t2.
There are no sixth, fifth, or fourth degree terms, and the third degree term is already next in line. You just need to swap the last two terms. -6t9 + 8t7 + 4t3 - 5t2 + lit is in standard form.
CHECK POINT
Put each polynomial in standard form.
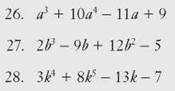
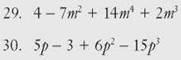
The Least You Need to Know
• A term is a constant, a variable, or the product of a constant and a variable.
• Terms are “like” if they contain exactly the same variables, raised to the same power, such as 27 and 107.
• Only like terms can be combined.
• To add or subtract like terms, add or subtract the coefficients and keep the variable part the same.
• A polynomial is a sum of terms using different powers of the same variable. A monomial has one term, a binomial has two terms, and a trinomial has three terms.