Basic Math and Pre-Algebra

PART 1. The World of Numbers

CHAPTER 2. Arithmetic

Multiplication and Division

There’s a lot of talk about the four operations of arithmetic: addition, subtraction, multiplication, and division. In a way, they all boil down to addition. As we’ve seen, subtraction is the inverse, or opposite, of addition. Multiplication is actually just a shortcut for adding the same number several times, and division is the inverse of multiplication. While each operation has its place, it’s good to remember that they’re all connected.

Multiplication

Multiplication originated as a shorter way to express repeated addition. Suppose you pay $40 every month for your phone. How much is that per year? You could say that you pay $40 in each of the 12 months of the year and write an addition problem 40 + 40 + 40 + 40 + 40 + 40 + 40 + 40 + 40 + 40 + 40 + 40. It’s long, but it would do the job. Multiplication lets you say the same thing as 40 X 12. (Or 12 x 40, thanks to the commutative property.) In this example, 40 and 12 are both called factors. When you multiply 40 by 12, you get 480, which is called the product.

DEFINITION

Each number in a multiplication problem is a factor. The result of the multiplication is the product. In the equation 5 x 3 = 15, 5 and 3 are factors, and 15 is the product.

Although it’s nice to have a shorter way to write the problem, multiplication isn’t much use to us unless it also gives us a simpler way to do the problem. And it will, but you need to do the memory work to learn the basic multiplication facts, or what most people call the times tables.

In the following chart, each column is one table or family of facts. The first column is the ones table, or what you’d get if you added one 1, two 1s, three 1s, and so on. The last column is the nines table. One 9 is 9, two 9s are 18, three 9s are 27, and on down to nine 9s are 81. (You’ll see some tables that include 10 and sometimes even larger numbers, and the more tables you can learn, the faster at multiplication you’ll be.)

Basic Multiplication Facts

The first column and top row show the single digit numbers. Each cell shows the product of the digits that start its row and column.

Once you’ve memorized the multiplication facts, you can take advantage of what you know about our place value system to handle larger numbers. Let’s start with something not too large. Let’s multiply 132 x 3.

You know that 132 means 1 hundred and 3 tens and 2 ones, and you know that multiplying by 3 is the same as adding 132 + 132 + 132. Instead of all that adding, you can multiply each digit of 132 by 3, using the 3 times table, and you get 396 or 3 hundreds, 9 tens, and 6 ones. Each digit, each place, gets multiplied by 3. 132 x 3 = 396.

Now let’s multiply 594 x 2. You have 5 hundreds, 9 tens, and 4 ones, and you want to multiply by 2. That should give us 10 hundreds, 18 tens, and 8 ones, but that means that you again face that problem of having a two-digit answer and only a one-digit place to put it. Just as you did with some of our addition, you’re going to need to carry.

Once again, you want to tackle that work from right to left. So, in this example, you start with 2 x 4 = 8 and that’s a single digit, so it can go in the ones place of the answer. Next, you multiply 2 x 9 = 18. That’s 18 tens. You break that into 1 group of 10 tens and another 8 tens, or 1 hundred and 8 tens. The 8 can go in the tens place of your answer, but you’ll hold on to the 1 hundred for a minute. Put a little 1 over the 5 to remind yourself that you have that 1 hundred waiting. One more multiplication, this time 2 x 5 = 10 hundreds, and then you’ll add on the 1 hundred that’s been waiting and you’ll have 11 hundreds. Of course, 11 hundreds form 1 group of 10 hundreds plus 1 more hundred, or 1 thousand and 1 hundred. Our multiplication ends up looking like this.

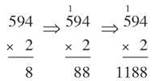
When all the multiplying and regrouping is done, 594 x 2 =1,188.

MATH TRAP

Remember that any carrying you do in multiplication happens after you do a multiplication. The digit you carry is part of the result of the multiplication. It has already been through the multiplication process, so make sure you wait and add it on after the next multiplication is done. Don't let it get into the multiplication again.

So our plan for multiplication of a larger number by a single digit is to start from the right, multiply each digit in the larger number by the one-digit multiplier, and carry when the result of a multiplication is more than one digit. That will work nicely when you want to multiply a larger number by one digit, but what if both of the numbers have more than one digit? What if you need to multiply 594 by 32 (instead of by just 2)?

For a problem like 594 x 32, you don’t have to invent a new method, but you do have to adapt the method a little. You’ll still start from the right and multiply each digit of 594 by 2, carrying when you need to. Then you’ll multiply each digit of 594 by 3, again starting from the right. But here’s the catch: that 3 you’re multiplying by is 3 tens, not 3 ones. You have to work that change in place value into your multiplication.

The problem is fairly easy to solve. Just look at the first time you multiply by the 3 tens: 3 x 4. It’s really 3 tens times 4, and that should give you not 12, but 12 tens or 120. Multiplying by 3 tens instead of just 3 simply adds a zero.

So here’s how you’ll tackle the problem. First you’ll multiply 594 by the 2, just as you did before.

Next, because you know that our next multiplication is by 3 tens and will add a zero, you’ll put a zero under the ones digits. Then you’ll multiply each digit of 594 by 3, carrying when you need to, and placing those digits on the line with that zero. It looks like this:

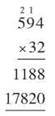
You start the second line of multiplication with the 0 on the right end, then multiply 594 x 3 to get 1782. Finally, you’ll add the two lines of results to get your final product.

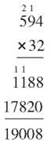
When you’re all done, you know that 594 x 32 = 19,008.

Notice that you’ve multiplied 594 by 2 and 594 by 30, then added those two products together.

The idea of adding that zero because you’re multiplying by a digit in the tens place can be extended to other places. If you’re going to multiply by a digit in the hundreds place, you’ll put two zeros at the right end of that line. If the digit you’re multiplying by is in the thousands place, you’ll start the line with three zeros.

Here’s a larger problem with very simple multiplication, so that you can see how the plan works.

You can see that the zeros shift each line of multiplication over one place, and that’s because each new multiplication is by a digit that’s worth ten times as much. The hardest part is all the adding, but when you’re done 11,111 x 345 = 3,833,295.

WORLDLY WISDOM

There's a method of multiplication that never requires you to multiply more than one digit by one digit and takes care of carrying automatically. It's called lattice multiplication. You make a grid of boxes with diagonal lines from upper right to lower left. Factors are written across the top and down the right side, one digit per box. Each multiplication of one digit by one digit goes in a box, with the tens digit above the diagonal and the ones below. Add along the diagonals, and read the product down the left side and across the bottom.

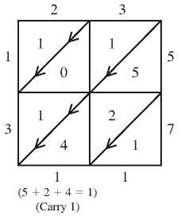
Are you ready for some multi-digit multiplication? Remember your basic facts, and don’t forget to add zeros to keep the place value columns aligned.

CHECK POINT

Complete each multiplication problem.

21. 462 x 53

22. 833 x 172

23. 1,005 x 53

24. 1,841 x 947

25. 2,864 x 563

Division

Division is the inverse, or opposite, of multiplication. If multiplication answers questions like “If I have 3 boxes of cookies and each box has 12 cookies, how many cookies do I have?” then division is for questions like “If I have 36 cookies and I’m going to put them in 3 boxes, how many cookies go in each box?” The division problem “36 ÷ 3 = what number?” is equivalent to “3 x what number = 36?”

DEFINITION

The result of a division is called a quotient. The number you divide by is the divisor, and the number you're dividing is called the dividend. Dividend -t divisor = quotient. In the equation 12 ÷ 3 = 4, 12 is the dividend, 3 is the divisor, and 4 is the quotient.

Just as knowing your addition facts helps with subtraction, knowing your multiplication facts, or times tables, will help with division. And just as you used the place value system to deal with larger numbers in other operations, a process called long division will use a similar strategy.

MATH TRAP

Division by zero is impossible. If you divide 12 by 4, you're asking 4 x what number = 12. If you try to divide 12 by 0, you're asking 0 x what number = 12, and the answer is there isn't one. Zero times anything is 0.

When you need to divide a number like 45 by 9, you can rely on basic facts (9 x 5 = 45), but if you need to divide 738 by 9, that’s not in the basic facts you’ve memorized.

The strategy you want to use instead has a logic, a way of thinking about what’s going on, and an algorithm, a step-by-step process for actually doing it. Algorithms can feel like magic, especially if you don’t understand the logic behind them, so let’s look at the logic first.

DEFINITION

An algorithm is a list of steps necessary to perform a process.

The number 738 is made up of 7 hundreds, 3 tens, and 8 ones. Think of them like paper money. You want to divide by 9. Look first at the hundreds. Can you deal out 7 hundred dollar bills into 9 piles? Not without leaving some piles empty, because there are 9 piles but only 7 hundreds. So exchange all the hundred dollar bills for ten dollar bills. 7 hundreds give you 70 tens, and the 3 tens you already had make 73 tens.

Can you deal the 73 tens out into 9 piles? You could deal 8 tens into each pile and have 1 ten left over. Okay, each pile has 8 tens. Take the extra 1 ten, trade it for 10 ones, and add on the 8 ones you already had. You’ve got 18 ones. Deal them out into the 9 piles, and each pile will get 2 ones. Each pile got 8 tens and 2 ones. That’s 82. 738 ÷ 9 = 82.

No one wants to think about all that dealing out and exchanging every time there’s a problem to be done, especially if the numbers are large. That’s why there’s an algorithm. Let’s look at the same problem with the algorithm. We set up the division problem with the divisor outside and the dividend, the number that’s being divided up, inside the long division symbol, or division bracket. As you complete the problem, the quotient will be written on top of the bracket.

Take the process digit by digit. How many 9s are there in 7? None, so you can put a zero over the top of the 7. Multiply the digit you just put in the quotient, 0, times the divisor, 9, and put the result under the 7. Subtract, and check that the result of the subtraction is smaller than the divisor. 7 is less than 9, so move on.

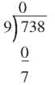
Those 7 hundreds change to 70 tens and get added to the 3 tens to make 73 tens. Show that by bringing the 3 down. Divide 9 into 73. It goes 8 times, so put an 8 up in the quotient. Multiply that 8 times the divisor, put the product (72) under the 73, and subtract. Check that the result is less than the divisor.

That’s the one leftover ten, which changes to 10 ones. Bring down the 8 to make 18 ones and divide 9 into 18. Put the 2 in the quotient, multiply 2 times the divisor, put the 18 under the 18 and subtract.

738 ÷ 9 = 82. You can drop that zero in the front, and in the future, you can just leave a blank space if the first digit in the quotient is a zero. Don’t drop any zeros that come later, though. They’re important place holders.

Long division doesn’t always work out to be as tidy as that last example. Sometimes you’ll get to the end of the dividend, with nothing left to bring down, but you’ll have something left over. For example, if you divide 49 ÷ 6, you’ll get a quotient of 8, but there will be 1 left over, because 6 x 8 is only 48. The leftover 1 is called the remainder. For now, just say you have a remainder. Later on, you’ll see other ways to handle it.

DEFINITION

A remainder is the number left over at the end of a division problem. It's the difference between the dividend and the product of the divisor and quotient.

Try a few problems to be sure you’ve mastered the algorithm.

CHECK POINT

Use the long division algorithm to find each quotient.

26. 4,578 ÷ 42

27. 3,496 ÷ 19

28. 16,617 ÷ 29

29. 681 ÷ 14

30. 1,951 ÷ 35

The Least You Need to Know

•  Addition and subtraction are inverse operations, as are multiplication and division.

•  Compatible numbers are number pairs that add up to ten. Looking for compatible numbers when adding and subtracting can allow you to complete the operation more quickly.

•  When performing operations with multi-digit numbers, keep the place value columns aligned.

•  The long division algorithm is a process that allows you to divide large numbers. To use this algorithm, remember: divide, multiply, subtract, compare, bring down, and repeat.