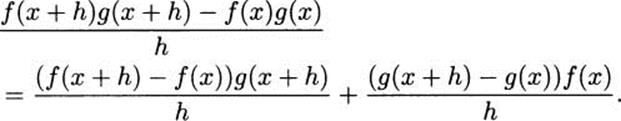The Product Rule and Quotient Rule - CALCULUS - MATHEMATICS IN HISTORY

Mathematics for the liberal arts (2013)

Part I. MATHEMATICS IN HISTORY

Chapter 4. CALCULUS

4.6 The Product Rule and Quotient Rule

Say we have two functions, f(x) and g(x). If we knew that the derivative of f(x) was 6 and the derivative of g(x) was 5, what would be the derivative of the product f(x)g(x)?

If you answered 30, you are probably not alone. But unfortunately you’re not right either, and you can easily check for yourself that this is a mistake. You could, for example, take f(x) = 6x. That’s a function with f′(x) = 6. If you also take g(x) = 5x, then g′(x) = 5. And when we multiply? We get f(x)g(x) = 6x · 5x = 30x². This means that the derivative of the product f(x)g(x) is then the derivative of 30x², and that is 60x, and not 30.

It turns out that there is a product rule for derivatives, but it is not the naively simple rule that most people guess.

The product rule: If we can compute the derivatives of f(x) and g(x), the derivative of their product is (f(x)g(x))′ = f′(x)g(x) + f(x)g′(x).

EXAMPLE 4.12

If we take f(x) = 6x and g(x) = 5x, then the product rule tells us that

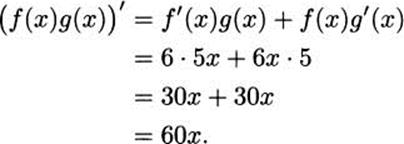
images

Naturally, this is the same as the answer we get without the product rule (when we do it correctly).

EXAMPLE 4.13

What is the derivative of

Solution: In plain English, the product rule tells us, “the derivative of a product is ‘the derivative of the first’ times ‘the second’ plus ‘the first’ times ‘the derivative of the second.’” Computing, we have

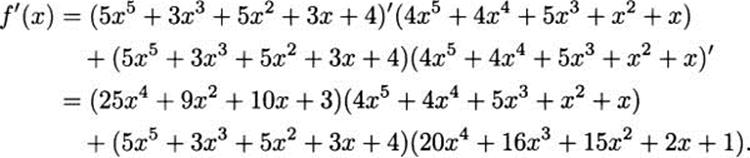
images

This may seem like an unsatisfyingly complicated answer, but it would be completely adequate if we were in a situation where we didn’t need to simplify. Although we devote extensive effort in algebra class to simplification, we don’t always need to simplify to solve problems. For example, if all we need to know is the slope of f when x = 0, it is straightforward to find that f′(0) = (3)(0) + (4)(1) =4, and the computation is easy even without simplifying.

EXAMPLE 4.14

We can use the product rule when there are more than two factors. We simply apply the product rule more than one time. Consider the function h(x) = x(x + 1)(x + 2). Although this function is easy to handle by multiplying things out, let’s use the product rule instead.

To get started, we have to decide which factors of the function will constitute the f(x) part of the product rule and which factors will be the g(x) part. It doesn’t really matter, as long as you split the function into two factors that are multiplied together. Let’s choose f(x) = x(x + 1) and g(x) = x + 2. Then h(x) = f(x)g(x), and we can differentiate:

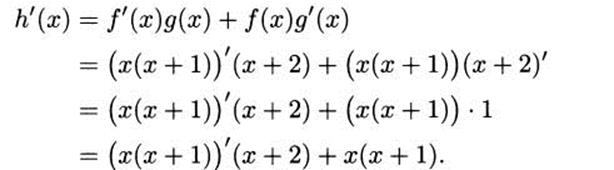
images

For the derivative of x(x + 1), we use the product rule a second time. Continuing,

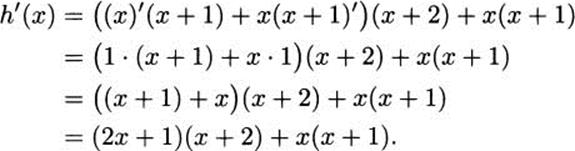
images

If we wish to combine terms and simplify a bit, we conclude that h′(x) = 3x² + 6x + 2. Of course, this is the same answer that we get if we multiply h out first and differentiate directly.

Naturally, we can differentiate functions that are products of four factors (it requires three applications of the product rule), or five factors, or more.

New Derivatives from the Product Rule

We can use the product rule to figure out the derivatives of functions we don’t yet know how to differentiate. For example, what is the derivative of f(x) = 1/x? We can use the product rule, if we are careful and clever.

If we start with f(x) – 1/x, then xf(x) = 1, which is a constant. Constant functions are easy to differentiate, so we know immediately that (xf(x))′ = 0. But we can also find the derivative using the product rule. According to the product rule,

Putting these two calculations together (remembering that f(x) = 1/x), we get

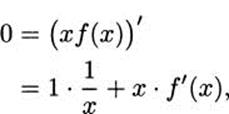
images

and it follows that

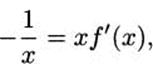
images

and finally that

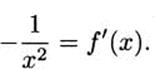
images

So if f(x) = 1/x, the derivative is f′(x) = –1/x².

The previous argument is an example of a common proof method in mathematics. If we can compute a quantity two different ways, then we know both answers must be equal even if they may not look the same. As in this discussion, often the clever step is figuring out how to arrange things (i.e., knowing to start with xf(x) = 1 and then differentiate). Once arranged, the calculations are not necessarily difficult.

EXAMPLE 4.15

Find the derivative of f(x) = .

Solution: We need to arrange things so we can use the product rule, so let h(x) = f(x)f(x) = = x. We can immediately see that h′(x) = 1, but we can also apply the product rule. This means that

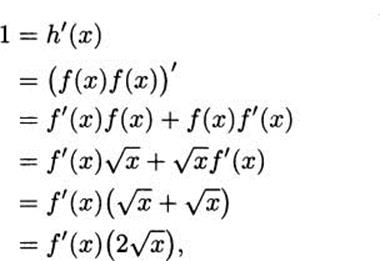
images

and dividing, we have

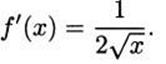
images

Just as we can find the derivative of products of functions, there is a rule for taking the derivatives of quotients of functions (that is, when we divide functions). The quotient rule is not easily guessed, but amazingly we can figure out the formula using the product rule.

First we need a quotient. Let h(x) = . Our goal is to find a formula for h′(x). When we cross-multiply, we get h(x)g(x) = f(x), or reversing the equality we have f(x) = h(x)g(x), and this is a product, so we can differentiate it. On the left, we’ll simply write the derivative as f′(x). On the right, we’ll use the product rule.

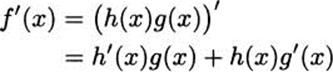
images

Now, keep the term with h′(x) on the right, and move everything else to the left side.

Reverse the equality and divide by g(x) to get h′(x) alone.

images

Next comes a clever part, but we’re almost finished. Remember that we started with h(x) = . Substitute for h(x) to get

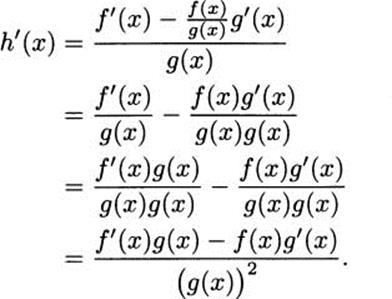
images

This becomes our rule for differentiating quotients.

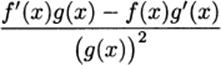The quotient rule: If h(x) = , then h′(x) = images .

Because this formula is fairly complex, people usually use one of two ways to remember it. In words we say that the derivative of a fraction is, “Bottom times the derivative of the top, minus top times the derivative of the bottom, all over the bottom squared.”

Some people prefer to remember the quotient rule via the (math) poem,

Read aloud, this goes, “Low dee-high, minus high dee-low, over low low (and away we go)!” In the poem, low refers to the bottom function g(x), high refers to the top function f(x), and dee reminds us to take a derivative. So ‘low dee-high" is g(x)f′(x). Similarly, “high dee-low” is f(x)g′(x). And we divide by “low low,” which is g(x) · g(x) = (g(x))². If you write everything out according to the poem, you get the quotient rule.

EXAMPLE 4.16

Let us apply the quotient rule to a function we already know the derivative of, such as x².

We can think of h(x) = x² as a quotient by writing it as h(x) = . Then, for the purposes of applying the quotient rule, f(x) = x² and g(x) = 1. We calculate

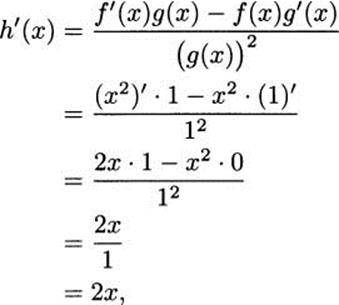
images

which we know is correct.

EXAMPLE 4.17

Find the derivative of h(x) = 1/x^k where k is a positive integer (1, 2, 3, etc.).

Solution: Take f(x) = 1 and g(x) = x^k. By the quotient rule,

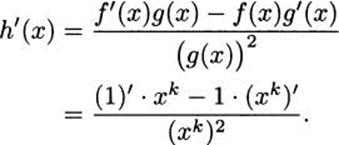
images

Here we can use the power rule to continue.

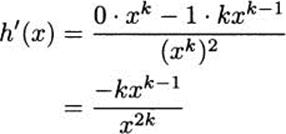
images

To divide powers, we subtract exponents.

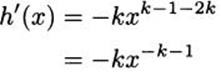
images

This completes the power rule. The computation we just finished verifies that the derivative of x^–k is –kx^–k–1. In other words, the power rule works with negative exponents. We now state the general power rule.

The power rule: If n is any integer (positive, negative, or zero), the derivative of the power function f(x) = xⁿ is f′(x) = nxⁿ^–1.

EXAMPLE 4.18

Find the derivative of h(x) = .

Solution: By the quotient rule,

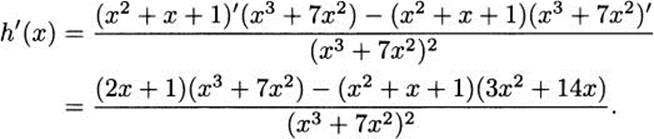
images

At this point, you may be inclined to simplify, but you should probably consider whether this gains you much. For example, if you merely need the slope of the function when x = 1, it is probably easier to evaluate h′(1) directly without simplifying. You’ll be less likely to make an error.

In this example, our goal was simply to find the derivative. We have done that, so we’ll stop here.

EXERCISES

4.27 Calculate the derivative of each function, once by multiplying out and also using the product rule. Verify that you get the same answer either way.

a) f(x) = x³(x + 4)

b) g(x) = (2x² + 7x + 7)(5x² + 4x + 5)

c) h(x) = (6x³ + 7x + 3)(2x³ + 8x² + 4x + 4)

4.28 For each function in the previous exercise:

a) Find the slope of the tangent line to the function when x = 0.

b) Find the equation of the tangent line to the function when x = 0.

c) Find the slope of the tangent line to the function when x = 1.

d) Find the equation of the tangent line to the function when x = 1.

4.29 Differentiate h(x) = x(x + 1)(x + 2) as we did in Example 4.14, only this time take f(x) = x and g(x) = (x + 1)(x + 2) as your factors for the product rule. Verify that you get the same answer.