Numbers: Their Tales, Types, and Treasures.

Chapter 11: Numbers and Philosophy

11.6.A FORMALIST'S DEFINITION OF NUMBER

Unlike a logicist, a formalist would not be concerned about the nature or meaning of number. He would accept any kind of objects, whether they exist in nature or in one's imagination, to play the role of numbers, as long as these objects satisfy certain properties qualifying them for that role.

The properties required for natural numbers were first described by Italian mathematician Giuseppe Peano (1858–1932). The Peano axioms are typically given in the form of five statements, which we will describe below. They formulate the properties of an otherwise-not-specified set, whose elements are called natural numbers. This description focuses on the intuitive idea that every natural number n has a unique “next number,” which is here called the “successor” S(n). Of course, what we have in mind is that the successor of n is simply n + 1, but at this stage addition has not yet been defined. The first Peano axiom singles out one element of the set as the first of the natural numbers and gives it the name “0.”

1. 0 is a natural number.

2. Every natural number n has a unique successor S(n), which is also a natural number.

3. There is no natural number that has 0 as successor.

4. Different natural numbers have different successors.

5. Any property that

a. holds for 0, and

b. holds for S(n) whenever it holds for n actually holds for all natural numbers.

The last axiom is the most difficult to understand. It is called the induction axiom and is an essential tool in proving properties of natural numbers.

As a set fulfilling these axioms, we could take, for example, the sequence of bullet points shown in figure 11.1:

Figure 11.1: A sequence of dots as a model for the Peano axioms.

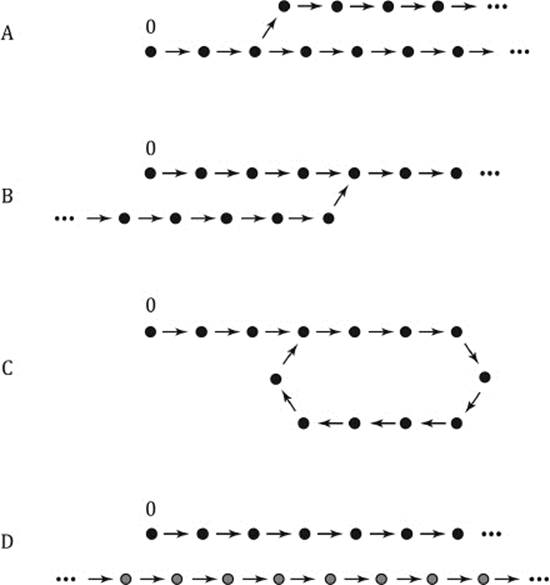
Figure 11.2: Counter examples to Peano's axioms.

In figure 11.1, it is assumed that the sequence of bullets can be continued indefinitely toward the right. In this set of points (they all look the same, but are distinguished by their position), the successor of any point is the next point to the right, as indicated by the arrow. We call the first and leftmost point “0.” This element is not a successor (axiom 3), but every other point is the unique successor of the point to its left (axiom 2). The set of points cannot end, because in that case there would be some point that has no successor, thus violating axiom 2. The other Peano axioms exclude, for example, the possibility of loops, bifurcations, or parallel chains of points. They also ensure that 0 is the only element without a predecessor. Hence, this simple chain of points starting at some point and extending indefinitely is, in fact, the only possibility. If you want to do an exercise in logical reasoning, you may look at the examples of point sets with a successor relation in figure 11.2. Each one of the sets A, B, C, and D, violates a particular Peano axiom. Can you figure out which Peano axiom is violated by which example? The solution will be given at the end of this section.

Starting with the element “0,” we obtain step-by-step all elements of the natural numbers by going to the successor: The successor of 0 will be called 1, the successor of 1 will be called 2, and so on:

1 = S(0),
2 = S(1) = S(S(0)),

and so on, and this sequence will never end. If we want to define, say, the addition of two numbers, we define first m + 0 = m and then m + S(n) = S(m + n).

From this definition, we can now derive, for example, that the successor of m is m + 1 because

m + 1 = m + S(0) = S(m + 0) = S(m).

And from here, it is not so difficult for a trained mathematician to develop the whole arithmetic of natural numbers.

It is very interesting that in all these considerations it was not necessary to assume anything about the nature of the elements in the set of natural numbers. This set could consist of counting words, of dots, or of the sets {Ø, {Ø}, {Ø, {Ø}},…} that were described in the previous section. The only thing that matters is that one can define a “successor function” for this set, which has the properties required by the Peano axioms. Once this can be done, the elements of this set can be just treated as natural numbers, and all further properties of natural numbers can be derived by logical reasoning from the Peano axioms. For the mathematical formalist, the nature of the objects that fulfill the Peano axioms is indeed irrelevant. All that counts is the mathematical structure that governs the behavior of these objects. And if these objects behave like numbers in every respect, a formalist would simply take these objects for numbers and go on to more important business.

It does not come as a surprise that Bertrand Russell was not at all happy with the formalist's point of view. He complains that

any progression may be taken as the basis of pure mathematics: we may give the name ‘0’ to its first term, the name ‘number’ to the whole set of its terms, and the name ‘successor’ to the next in the progression. The progression need not be composed of numbers: it may be composed of points in space, or moments of time, or any other terms of which there is an infinite supply…. It is assumed that we know what is meant by ‘0,’ and that we shall not suppose that this symbol means 100 or Cleopatra's Needle or any of the other things that it might mean…. We want our numbers not merely to verify mathematical formulae, but to apply in the right way to common objects. We want to have ten fingers and two eyes and one nose.¹³

Solution to the exercise in logical thinking:

A:This set violates axiom 2, since there is a point whose successor is not unique, because it has two successors.

B:Violates axiom 4 because two different points have the same successor.

C:Again violates axiom 4 because two different points have the same successor.

D:Violates axiom 5. The set D contains two sequences of dots, which are not connected by the successor property. For clarity, they are distinguished by color. 0 is black and for every black point, also its successor is black. Hence, by axiom 5, all points should be black, which is obviously not the case. (The color is not really necessary for this argument. Instead of the property “black,” we could use in the same way, for example, the property “being a point in the upper row.”)