Numbers: Their Tales, Types, and Treasures.

Chapter 11: Numbers and Philosophy

11.7.THE STRUCTURALIST'S POINT OF VIEW

Structuralism is a philosophy of mathematics that evolved in the second half of the twentieth century. It holds that mathematical objects, like numbers, are only meaningful as parts of a larger structure. In order to understand this point of view, we need to go back to chapter 1, where we dealt with numbers in the context of counting. We learned that counting is done according to certain principles, and we saw how these principles imposed a certain structure on the set of number words. According to structuralism, number words do not refer to “abstract numbers.” They have no meaning in their own right; they get their meaning exclusively from the structure of the whole set of number words.

The number words “one,” “two,” “three,”…are distinguished by their strict and invariable ordering. This strict order of that sequence implies that any particular number word, for example, “eight,” defines in a unique way a part of the sequence of the number words. This is the initial sequence of all number words from “one” to “eight”:

“eight” ⇒ (“one”, “two”, “three”, “four”, “five”, “six”, “seven”, “eight”).

When we count a set and find that it contains eight elements, this simple statement actually means that this set contains exactly as many elements as there are number words in the initial sequence defined by “eight.” This means that there is a one-to-one correspondence between the given set and the initial section, “one” through “eight,” of the sequence of number words (see figure 11.3).

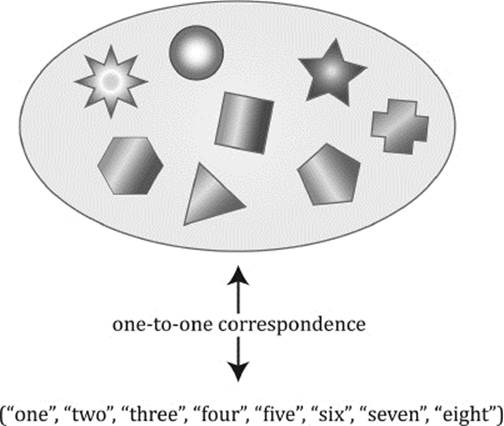
Figure 11.3: “This set has eight elements.”

As explained in chapter 1, the statement “This set has eight elements” is actually an abbreviation for “There is a one-to-one correspondence between the set and the initial section of the sequence of number words up to ‘eight.’” This latter sentence describes precisely what we do when we count a collection of objects. We point with a finger to each of the objects in turn, tagging each with a number word and using the number words in a strict order. In that way, we pair each object with a number word, thereby establishing the one-to-one correspondence between the objects and the initial section of the number-word sequence. The last number word in that initial section has been called the cardinal number of the set.

The whole procedure is reported in an abbreviated form—“There are eight objects.” The short form does not mention the initial section of the number-word sequence and its relation with the set of objects. This gives the impression that “eight” is a property of the collection of objects, while the statement “there are eight objects” actually tells us something about the relation between a set of objects and a certain part of the number-word sequence.

In the discussion above, the English number words just served as an example. Another sequence of counting tags—for example, the German number words (like “eins,” “zwei,” “drei,”…)—would serve the same purpose. Any set of words or symbols that can be arranged in a linearly ordered sequence could serve as a sequence of counting tags. In a more universal fashion, we could just use the ordered sequence of symbols: (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,…) in the same way as we use number words, for tagging the counted objects. The sentence “a set has 8 elements” is a short form of the statement that there is a one-to-one correspondence between the set and the initial section (1, 2, 3, 4, 5, 6, 7, 8) of the symbol sequence.

If taken in this sense, the symbol “8” (or the word “eight,” or any other symbol or word that we might use in counting) does not refer to any particular mathematical object at all. It is the ordered structure of the whole sequence that makes its members suitable for the purpose of counting, not a property of the individual members of the sequence. The individual number is meaningless; the meaning lies in the structure of the number sequence. This point of view was expressed by German mathematician Hermann Weyl (1885–1955) in the article “Mathematics and the Laws of Nature” as follows: “But numbers have neither substance, nor meaning, nor qualities. They are nothing but marks, and all that is in them we have put into them by the simple rule of straight succession.”¹⁴ American mathematician Paul Benacerraf (1931–), who is one of the main proponents of structuralism in mathematical philosophy, writes in his article “What Numbers Could Not Be”: “What is important is not the individuality of each element, but the structure which they jointly exhibit.”¹⁵ He argues that it is utterly pointless to ask whether any particular set-theoretic object, like the set {Ø, {Ø}}, could replace the number 2 because “‘objects’ do not do the job of numbers singly; the whole system performs the job or nothing does.”

Moreover, this type of identification of a “number” with a mathematical object could never be done in a unique way. Therefore Benacerraf comes to the conclusion “that numbers could not be objects at all; for there is no more reason to identify any individual number with any one particular object than with any other.”¹⁶ For arithmetical purposes, all that matters is that the collection of numbers has the structure of a linear progression. Additional individual properties of numbers would not matter at all; they are of no consequence to arithmetic. He continues, “but it would be only these properties that would single out a number as this object or that.” Hence the question of whether a number is any particular sort of abstract object is completely irrelevant. This question misses the point of what arithmetic is all about. The arithmetic of natural numbers is the science of describing the structure of a linear progression. This is the structure of all ordered sequences where we have a first element and where each element has a successor, as described in the Peano axioms (see section 6). Arithmetic is not the search for which particular objects the numbers really represent—“there is no unique set of objects that are the numbers. Number theory is the elaboration of the properties of all structures of the order type of the numbers. The number words do not have single referents.”

Mathematical structuralism emphasizes the description of structural properties as the real goal of mathematics. Therefore, it has much in common with formalism, but to a structuralist the purely formalist point of view that mathematics is just a game played according to certain rules with meaningless symbols goes too far. The statement “this set has 8 elements” does have a definite meaning. But the meaning of “8” (or “eight” or “acht”) can only be explained if we know the position of that element within the whole sequential structure to which it belongs. It is not a property of the individual member of the sequence, but its relation to the other members of the sequence that gives a meaning to the number word or symbol.

The structuralist point of view says that “8” does not refer to an abstract object. This is in accordance with a modern linguist's point of view. After a linguistic analysis, German scholar Heike Wiese (1966–), in her book Numbers, Language, and the Human Mind, also comes to the conclusion that number words are nonreferential—a number word does not refer to any real or abstract object; it just works as an element of the number-word sequence. Number words are special because “unlike other words, they do not have any meaning, they do not refer to anything in the outside world. This is because they are not names for numbers, they are numbers. Counting words are tools that we use in number assignments, and for this job they do not need any referentiality.”¹⁷