Numbers: Their Tales, Types, and Treasures.
Chapter 3: Numbers in History
3.6.NUMBERS IN INDIA
In old India, about 1,500 years ago, a revolution took place that still influences our life today. Indian scholars invented a decimal place-value system with a concept of the number zero—not only as a symbol, but also as a quantity that could be used for counting and for calculations. It was not the first place-value system, and not the first decimal system, but it is the one that is still in use today.
India is a large country with many languages and subcultures; hence the language of the scholars has always been Sanskrit. Being scientists and poets at the same time, Indian scholars expressed everything in verses, even purely mathematical results—making use of the many verse meters available to them to reduce monotony. Moreover, they used an obscure and mystic way of speaking that is often unintelligible. It appears that the pure facts and methods were well known to them and were passed on by oral tradition. The written text just served to aid memory without providing too many details.
In particular, astronomy was a highly developed science, and much of present-day trigonometry was developed in the centers of astronomical research, in Ujjain and Pataliputra (Patna). Indian astronomers had a need for large numbers and developed a deep fascination for them.
At the beginning of the first millennium CE, the numeral system that was in use in India was not a place-value system. It was, actually, rather limited for scientific purposes and did not allow the representation of large numbers. It was also somewhat impractical because it contained too many different symbols. For example, they had special symbols for each of the numbers 10, 20, 30,…90, 100, 200, 300,…900, and so on. For us, this numeral system is of interest because it had digits for the numbers 1 to 9 that were “graphically designed” for easy distinguishability. There were numerous different writing styles for these symbols. A sample set (adapted from Ifrah) is shown in figure 3.13.2 These symbols are predecessors of the digits that are in use today.

Figure 3.13: Digits derived from Brahmi writing.
In written text, however, Indian scholars did not use these symbols at all. Instead, they used the number words of Sanskrit to express numbers verbally. In addition to the number words for one to nine, Sanskrit has a number word for every power of 10 (see table 3.5).
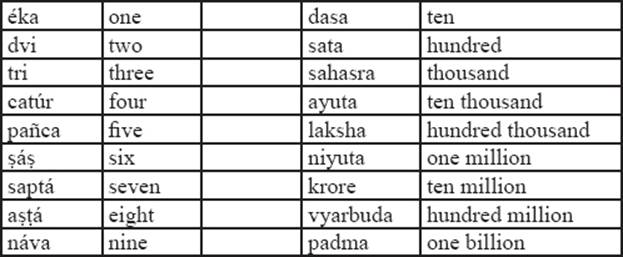
Table 3.5: Sanskrit number vocabulary.
The sequence of number words for powers of 10 could even be continued to very high powers of 10, up to 1053.
In the verbal description of a number, the scholars would name the units first and proceed to higher powers of 10, which is just the opposite of our present-day custom. For example, the numeral 4567 would have been expressed by saptá ṣáṣti pañcasata catúrsahasra (meaning “seven, sixty, five hundred, four thousand”).
Very long numbers (for example, those used in astronomical texts) would therefore result in very long chains of words, which were difficult to incorporate into a verse. Probably at the beginning of the fifth century CE, a great idea evolved that helped to represent numbers more efficiently. In order to shorten the verbal expression of very long numbers, they did not pronounce the powers of 10 any longer and just kept the names of the units. In the example above, they would just say “seven-six-five-four.” It was not necessary to say more, because the number words were always given in the same strict order of increasing powers of ten, and the Indian writers were, indeed, very conscious about this and had a special word, sthanakramad (meaning “in the order of position”), to describe this. So the spoken system was actually a place-value system.
In the written numeral place-value systems of Babylon and China, missing orders of magnitude had to be expressed by leaving a space. But this is not possible in a spoken system. So they put the word śūnya, which means “void,” in place of the missing number. For example, they saiddvi-śūnya-tri to distinguish 302 from dvi-tri, meaning 32. The oldest historical record of this “verbal positional system with zero” seems to be the Lokavibhāga, a treatise on cosmology, dated to 458 CE.
From the point of view of poetry, there was still a problem. Some results required a frequent repetition of one of the “digits.” For example, one of the hypothetical cosmic cycles of Indian astronomy, the mahāyuga, lasted 4,320,000 years. This number would have to be represented by the following:
śūnya śūnya śūnya śūnya dvi tri catúr (void-void-void-void-two-three-four),
which is rather dull reading. So they had the idea to replace individual number words by other words, such as a verse metric often motivated by their aesthetic feeling for poetry. Each number word acquired many substitute words, which were also associated with that number. For example, the word śūnya, meaning “void” or “empty,” could be replaced with the word for sky, atmosphere, or space, to name a few. As an example from a text of the year 629, Georges Ifrah reports the following:3
viyadambarakasaśūnyayamaramaveda = 4,320,000
This term consists of the words sky-atmosphere-space-void-Yama-Rāma-Veda, meaning
0-0-0-0-2-3-4.
In Hindu mythology, Yama, who later became the Hinduistic god of death, lived on Earth together with his twin sister, Yami, as the primordial couple. Thus, his name was associated with “two.” Rāma was associated with “three” because of three famous persons with that name (two of them incarnations of Vishnu, and the third being the hero of the epic saga Rāmāyaṇa). Veda is used as a word for four because the Veda, the main religious text of Hinduism, consists of four principal books.
There are many different words that could be used to express any number from zero to nine. In that way, even boring numbers could be turned into poetic verses. Texts written with that representation of numbers presented no problem for the Indian astronomers but were almost unreadable for the uninitiated. For the scholars, the verbal style even added to clarity because the Indian numeral symbols evolved in many different ways in various parts of India. Moreover, large differences in handwriting sometimes made the numeral symbols even more difficult to interpret than the verbal expression. Using the poetic representation, even little errors would have been noted because the substitution of a wrong word would probably have disturbed the rhythm of speech (that is, the metric of the verse).