Numbers: Their Tales, Types, and Treasures.
Chapter 3: Numbers in History
3.7.SYMBOLIC NUMBER NOTATION AND THE ABACUS IN INDIA
The Indian verbal place-value system was not suitable for doing calculations. As with the Chinese, the Indians used the counting board, or an abacus, for practical calculations. The abacus is particularly important for the development of the place-value system. It was in use throughout the antique world. Long before it became the familiar counting frame with beads sliding on wires, it was just a board with vertical columns. Perhaps the simplest form is a sand abacus, a plane surface with fine sand on it, on which vertical lines are drawn with a pointed tool to separate the columns. Initially, numbers were represented by putting appropriate numbers of sticks or pebbles into the columns. (Recall the method of counting using pebbles, sticks, bones, shells, etc., as described in section 1.10.) The new idea here is that it is not necessary to use different kinds of objects in order to represent different orders of magnitude. Instead, one uses only one kind of object—for example, little pebbles (called calculi by the Romans). The order of magnitude is then represented by the column in which the pebbles are placed. Figure 3.14 shows, as an example, the same number as the one in figure 1.8, but this time realized on a sand abacus.
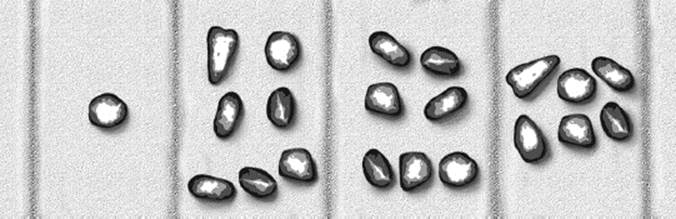
Figure 3.14: The number 1776 on a sand abacus.
The older method of figure 1.8 has the advantage that you can put everything into a bag and the number would still be preserved properly. The abacus, on the other hand, is made not for storing numbers, but for doing calculations. For example, when adding two numbers, you would simply add the pebbles in each column, and, as soon as the number in one column exceeds 10, you would remove 10 pebbles from that column and add one pebble to the next column.
The columns of an abacus, holding the ones, the tens, the hundreds, and so on, actually realize a place-value system: The first and rightmost column usually contains the units, the next column to the left represents the tens, the next column the hundreds, and so on. Quite early, the Indian scholars had the idea to write the symbols for the digits into the columns instead of placing pebbles or sticks. Thus, the number 1776 of figure 3.14 would then appear as in figure 3.15.
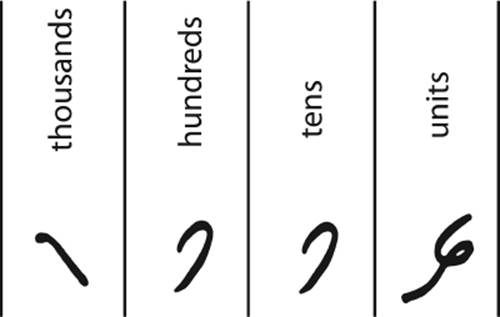
Figure 3.15: The number 1776 with Indian symbols written on an abacus.
Over time, the symbols used for calculations with an abacus also appeared in the writings of scholars. To make things more complicated, whenever the symbols appeared in a text (written from left to right), the order of the digits was reversed, in order to match the way the number words were written—starting with the units. Thus, the number 1776 would appear as 6771 in written form. An even more important difference between numbers on an abacus and numbers in writing has to do with the representation of zero. With an abacus, there was no need for a symbol denoting zero, because a missing order of magnitude would have been represented by an empty space. But in a written text, the symbols provided an abbreviation of the verbal number representation in Sanskrit, which frequently contained the word śūnya or one of its equivalents to denote the void, the absence of a “digit.” Probably around the year 500, Indians had the idea to represent śūnya by a special symbol, a dot or a small circle (which later became our symbol 0). Still, the direction was reversed: 3200 would have been something like “sky-atmosphere-Yama-Rāma,” or 0023, if written in symbols.
On an abacus, calculations were performed by writing digits in the columns and manipulating them according to very complicated rules that took a long time to learn. At the beginning of the sixth century, it was recognized that the symbol for zero could also be of use when performing calculations. The advantage was that the columns of the abacus were no longer needed, because the symbol for śūnya could be used for the empty column. The familiar calculations and manipulations of numbers could be done directly with the digits, without having to draw the columns first, because their value is uniquely determined by their position within the number. So mathematicians could do all computations in the same way as on the abacus. Hence, they became more and more used to numerals written in abacus-notation—with the rightmost digits representing the units. As a consequence, the direction of writing numerals was also changed to reflect the order of digits made familiar from the abacus. And now, as a result of a long development, the number 4,320,000 years in the cosmic cycle mahāyuga, finally, would have been written as shown in figure 3.16, which is the same way we do it today.

Figure 3.16: The number 4,320,000 in “modern” notation.
However, the notation enables a smooth transition from the abacus to written form. For example, the large repertoire of algorithms for doing calculations, which have been developed over centuries for the abacus, would then immediately be transformed into written form. The fact that the numbers and the calculations became independent of the abacus had important consequences. The digit zero gradually became a number. It was used not only as a symbol for an empty column of an abacus but also as something with which one can perform calculations, such as 5 – 5 = 0, or 5 + 0 = 5, or 5 × 0 = 0. Another important side effect of transferring calculations from an abacus to paper (or, rather, sheets of birch bark) was that intermediate results did not have to be erased, so it was easier to track down errors or rethink the applied methods in the search for simplifications. The complicated methods and rules used for calculations with an abacus could be gradually simplified; calculations could be done faster and more effectively. All this had an enormous impact on the mathematical sciences and astronomy, which in the following centuries experienced an unprecedented boom in India.
This was the state of art when Brahmagupta (598–668 CE), one of India's greatest mathematicians, was the head of the astronomical observatory of Ujjain. In the year 628 he wrote the famous book Brahmasphutasiddhanta (“Treatise of Brahma”). It used the decimal system, described the role of zero, and formulated, in particular, precise rules for doing calculations with zero. Moreover, Brahmagupta had rules for dealing with negative numbers and methods for computing square roots, solving equations, and much more. During the reign of the caliph al-Ma’mun (786–833 CE), Brahmagupta's text found its way to Baghdad and was translated into Arabic. Thus the information about the Indian numeral system spread from India into the expanding Arab world, where its ingenuity and importance was quickly recognized. In 825, Persian mathematician Muḥammad ibn Mūsā al-Khwārizmī (ca. 780–850), a scholar in the House of Wisdom, in Baghdad, wrote a book titled On the Calculation with Hindu Numerals. In Europe, the name al-Khwārizmī later developed into the word algorithm. Another book by al-Khwārizmī, titled al-Kitab al-mukhtasar fi hisab al-jabr wa'l-muqabala (“The Compendious Book on Calculation by Completion and Balancing”) contained the word al-jabr in its title, which is the origin of the word algebra.
Thus, the Indian numeral system spread quickly throughout the Arab world, where culture and science were highly esteemed. Europe, at the same time, was in a period of economic decline and was culturally and scientifically backward. Thus it took another five hundred years until the Indian digits and numeral system finally reached Europe.