Numbers: Their Tales, Types, and Treasures.

Chapter 5: Counting for Poets

5.8.THE ART OF COMBINATION

The Indian scholars also gave the answer to an even-more detailed and sophisticated problem: In how many ways can one combine a given number of short and long syllables into a verse? In honor of Pingala, we call this “Pingala's third problem.”

Pingala's third problem:

How many different verse meters exist that have a total length of n syllables, among which are precisely k short syllables?

This is the same question as: In how many ways can we combine k short syllables and n – k long syllables? Here n is any natural number, but k can only have values between 0 and n. In the case of k = 0, the verse meter has only long syllables, and k = n means that it has only short syllables.

As in the case of Pingala's first problem, this one too is just a prototypical case of similar problems that are important in many different contexts. Indeed, big money is earned nowadays by exploiting the solution to this problem in lotto games. But more on this later.

We will approach Pingala's third problem step-by-step. As with Pingala's first problem, we start by giving the unknown number a name:

· The number of meters with k short syllables and a total of n syllables will be called B(n,k).

It is often useful to approach a problem with a graphical illustration. Let us draw a single point on a piece of paper. This point should represent the beginning of the verse. From here, the verse may start either with a long or with a short syllable. These two alternatives will be shown in a “decision tree” by two arrows marked as L (“long”) and S (“short”), as in figure 5.4.

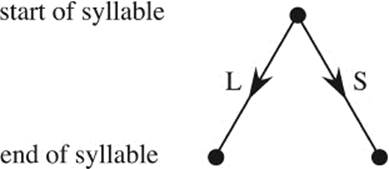
Figure 5.4: Two possibilities for the first syllable—long (L) or short (S).

What we have obtained so far, is B(1,0) = 1 and B(1,1) = 1. After the first syllable, the verse can continue in the same way. In figure 5.5 we see all possible steps that lead from the beginning of the verse to the end of the second syllable: LL, LS, SL, and SS. And this describes all possible verse meters consisting of four syllables.

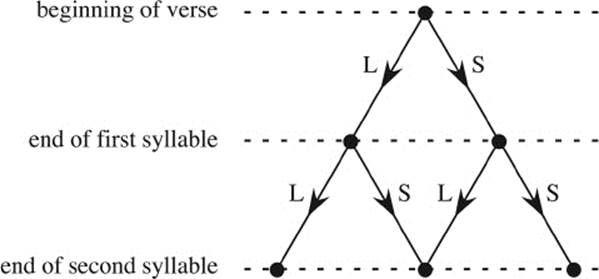
Figure 5.5: Four possible paths lead to the end of the second syllable.

You can see that the two verses with the pattern LS and SL (trochee and iamb) end at the same point in the middle. This just indicates that both meters take the same time (three moras). If we count the time needed to reach the end of the second syllable by moras, as before, we find that it takes two moras (two short syllables) to reach the rightmost point, three moras to reach the point in the middle, and four moras to reach the leftmost point.

We collect our results for the second row of points:

B(2,0) = 1, B(2,1) = 2, and B(2,2) = 1.

We continue to build the decision tree and add a line to the diagram for each additional syllable. Every path leading down from the top of the diagram determines a particular sequence of L and S syllables, and hence a particular verse meter. In figure 5.6, the marked path describes a seven-syllable meter with the pattern SLSLSSL = ˘ ¯ ˘ ¯ ˘ ˘ ¯ (as in “I'd like to see you tonight”).

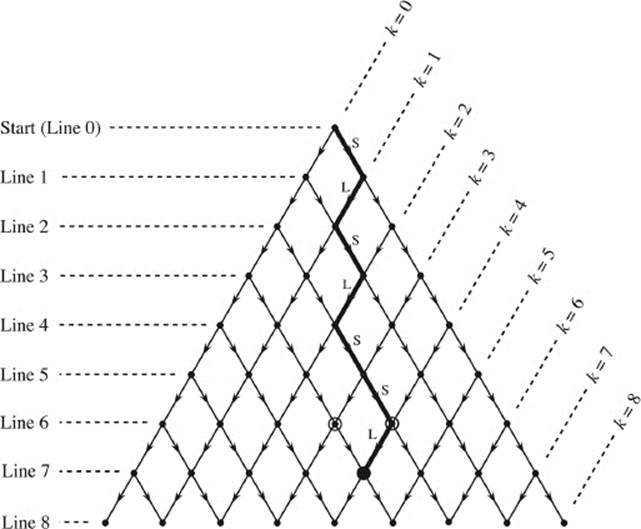
Figure 5.6: Decision diagram for verse meters with up to eight syllables.

Each point in the diagram can be identified by its line number and its place within that line. Note that line n marks the end of the nth syllable. The distance from the left side is described by the number k. In line n, the leftmost point has k = 0, and the rightmost point has k = n. Now every point in the diagram can be addressed by giving two numbers or “coordinates,” the line number n and the (horizontal) distance k from the left: A general position in the diagram is (n, k), where k is between 0 and n. For example, the fat point in figure 5.6 has the coordinates (7,4) because it is in line 7 and 4 steps from the left border of the diagram. The top of the diagram has coordinates (0,0).

When you follow any path through the diagram that starts at the top, the number k is increased for every “S-step.” In an “L-step,” the number k is not changed. Any path in the diagram that ends at, say, k = 4, thus contains precisely four “k-steps” and corresponds to a verse with four short syllables. The coordinate k just counts the number of short syllables in the verse!

Thus, when we ask for the number B(n,k) of verse meters with a total of n syllables of which k are short, we want to know the number of paths ending in line n at position k in the decision tree. And of course, the only allowed paths are those starting at the top of the diagram and going down in the direction of the arrows. A path going “upstairs” wouldn't mean anything. We have now found an important property of the number B(n,k):

B(n,k) = number of paths starting at (0,0) and ending at (n,k).

What have we gained now? Instead of counting possible verse meters, we now have to count the paths through a diagram, which doesn't appear much easier. At least we can now follow the paths with a finger and list all possible arrangements of long and short syllables. This works well for short verses. For example, we can find all verse meters ending in line 3 at position k = 2: LSS, SLS, and SSL (which today would be called dactyl, amphibrach, and anapest). This means, that B(3,2) = 3. We also notice that for all natural numbers n = 1, 2, 3…

· B(n,0) = 1, for all n = 1, 2, 3…(only one path ends at the left border of line n).

· B(n,n) = 1, for all n = 1, 2, 3…(only one path ends at the right border of line n).

If you try to count all possible paths ending at a particular point in the decision diagram, you will notice that this soon becomes rather difficult. Or can you easily find all thirty-five different paths that end at the point (7,4) in figure 5.6? Before we try to determine all the numbers B(n,k) by actually counting all possible paths in the diagram, it is perhaps better to sit down thinking a bit more about their properties.