Numbers: Their Tales, Types, and Treasures.

Chapter 5: Counting for Poets

5.9.SOLVING PINGALA'S THIRD PROBLEM

In the section about Pingala's first problem, we were successful by “working backward.” We were able to determine the number A(n) with the help of the previous numbers A(n – 1) and A(n – 2). Perhaps a similar strategy will work here too?

Indeed, in figure 5.6, look at the fat point in line 7. How many paths lead to that point? All these paths obviously have to come from one of the two marked points in the previous line 6. Now we have just to add up all the paths leading to one of these two points in order to obtain the desired result. Thus we observe:

Number of paths leading to (7,4) = number of paths to (6,3) plus number of paths to (6,4).

As a formula, we can write this as follows:

B(7,4) = B(6,3) + B(6,4)

This observation is obviously true for all points in the diagram: The number of paths ending in a particular point is the sum of the paths leading to the immediately adjacent points in the line above. The points at the border are an exception to this rule, but we know already that there is only one path to each of the border points.

Now, let us write in the diagram the number of paths leading to each point. The prescription above gives us an easy method to determine the number of paths step-by-step. We write the results directly into the tree diagram, as in figure 5.7.

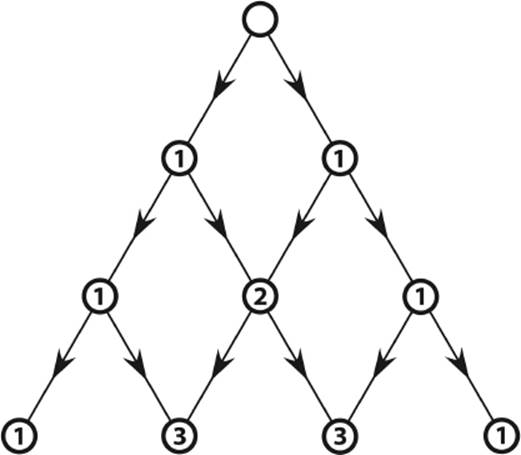
Figure 5.7: First lines of the decision tree with the numbers B(n,k) that count the number of paths leading from the top to that point.

It is now fairly easy to continue because we know that by adding two adjacent numbers, we obtain the number directly below. We can place “1” on all border points because we already know that only one path connects the border. For the sake of completeness, we put “1” even at the top—that is, we make the definition that B(0,0) = 1. The remaining places are then filled by simply adding the two adjacent numbers in the line above, as shown in figure 5.8.

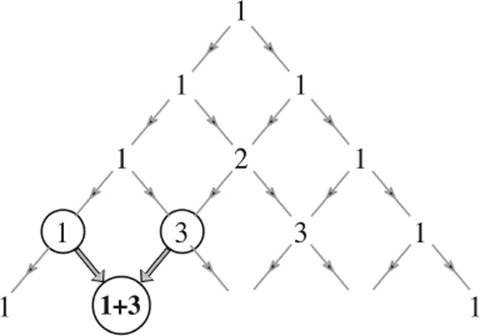
Figure 5.8: Constructing the numbers B(n,k) step-by-step.

If we continue in this manner, by writing at each place the sum of the two nearest neighbors in the row above, we obtain a triangular table of numbers that can be continued indefinitely. Only our patience and the available space provide a natural limit (see figure 5.9). Here, for the sake of simplicity, we even omitted the arrows.

Indian astronomer and mathematician Varāhamihira (ca. 505) also knew the numbers B(n,k), and he computed them in the way described above. The oldest record of the triangular arrangement seems to be in the writings of the Indian scholar Halayudha, who in the tenth century explained Pingala's findings. In Halayudha's commentary on Pingala's verse metric, this triangle is called the Meru Prastara, the “staircase to Meru.” Halayudha saw in it a symbolic representation of the sacred Mount Meru, a mythological mountain in Hindu cosmology.

Like the Fibonacci numbers, the arithmetic triangle in figure 5.9 has been rediscovered often in other regions of the world. Shortly after its appearance in India, it was known in China to the palace eunuch and mathematician Jia Xian (1010–1070). Later, Yang Hui (about 1238–1298) explained its use in detail, quoting Jia Xian as his source. Unfortunately, the original source was lost and the triangle became known as Yang Hui's triangle in China. Figure 5.10 shows an early drawing of Yang Hui's triangle. The numbers in the circles are written using so-called rod numerals.

Figure 5.9: Meru Prastara, or Pascal triangle.

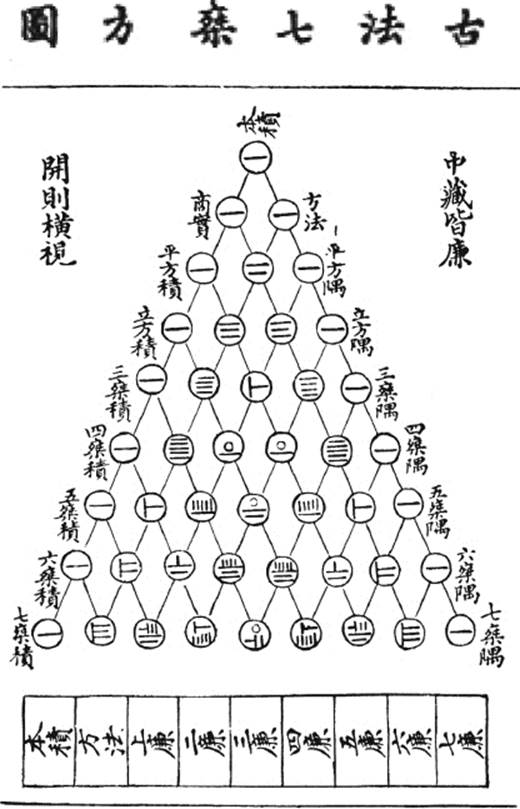
Figure 5.10: Yang Hui's triangle in a drawing from the year 1303.
(From Wikimedia Commons, user Noe.)

About at the same time as in India, the arithmetic triangle was discovered by Al Karaji (ca. 953–1029) in Baghdad and later again by Omar Khayyām (1048–1131). Hence in Iran, it is known as the Khayyām triangle.

In Germany, the Renaissance scholar Peter Apian (1495–1552) was the first to publish the arithmetic triangle in Europe. In Italy, the triangolo di Tartaglia is named after Nicolo Tartaglia (1499–1557), a mathematician who is famous for finding a formula for solving cubic equations. In the modern Western mathematical literature, the triangle in figure 5.9 is known as the Pascal triangle after Blaise Pascal (1623–1662), who used the properties of the triangle to solve problems in probability theory. Pascal's Traité du triangle arithmétique (“Treatise on an Arithmetical Triangle”) was published posthumously in 1665. His version of the triangle is shown in figure 5.11.

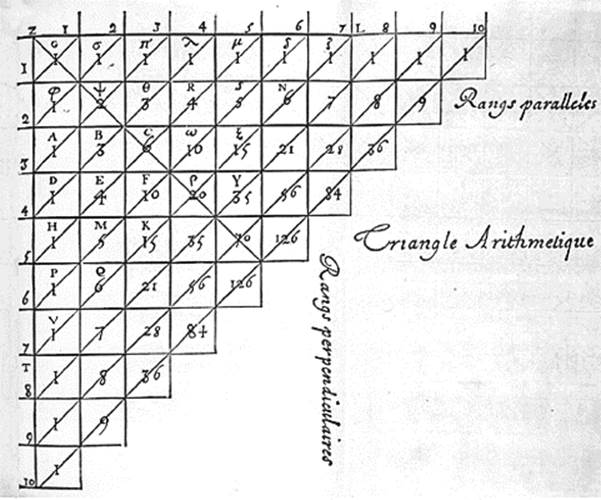
Figure 5.11: Pascal's version of the Pascal triangle.
(From B. Pascal, Traité du Triangle Arithmétique, 1654.)