Numbers: Their Tales, Types, and Treasures.
Chapter 6: Number Explorations
6.2.GENERATIONS OF RABBITS
Another stimulating question about the rabbit problem would be the following: How many pairs of rabbits belong to a particular generation of rabbits in a given month? Table 6.2 provides the answer. It shows the number of rabbit pairs for each month, ordered according to the generation to which they belong. Originally, we started with a single pair constituting the first generation. This pair is always there because Fibonacci rabbits never die. The children of the first pair are listed in column 2; they belong to the second generation. Starting with month 2, the original pair gives birth to a new pair each month; consequently, the number of second-generation pairs increase by one each month. The third-generation pairs are the children of the second-generation rabbits, or the grandchildren of the original pair.
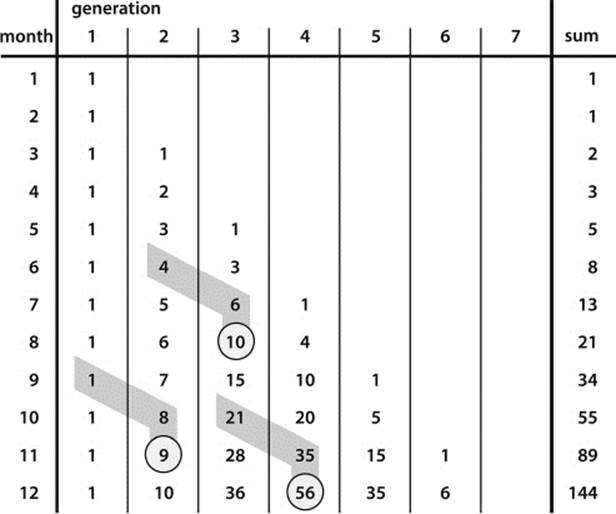
Table 6.2: Number of Fibonacci rabbits per generation.
Let us consider the number of pairs of the kth generation in month m. We denote this number by S(m,k). This number consists of
· all rabbits of kth generation that existed already in the month before (= S(m – 1,k)), plus
· the number of the newborn pairs of the kth generation.
However, the number of newborn pairs is exactly equal to the number of parent pairs (belonging to generation k – 1) that existed two months earlier, that is, S(m – 2,k – 1). Therefore,
S(m,k) = S(m – 1,k) + S(m – 2,k – 1).
That is, the numbers S(m,k) are obtained as the sums of two previously obtained numbers, as indicated for the numbers 9, 10, and 56 in table 6.2. With this rule you could easily compute further entries to the chart in table 6.2.
Perhaps you have already recognized the similarity of the numbers in table 6.2 with the numbers in another arrangement, the Meru Prastara, or Pascal triangle, detailed in section 5.9. In fact, the chart in table 6.2 is just a distorted version of the Pascal triangle, whose entries have now received a new interpretation, namely as the number of pairs of Fibonacci rabbits belonging to a certain generation in a certain month. The columns in table 6.2 are the steep diagonals of the Pascal triangle; the rows are the shallow diagonals. This interpretation of the Pascal triangle is shown in figure 6.2, where the black lines correspond to the rows and the gray lines to the columns in table 6.2.
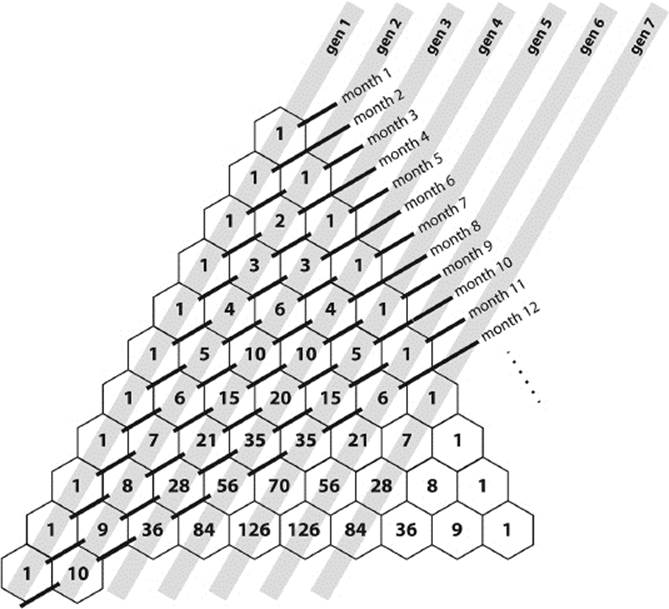
Figure 6.2: Pascal triangle and rabbit generations.
The consideration above offers an alternative to the approach described in chapter 5 that led us to Meru Prastara, the old Indian version of the Pascal triangle. However, this path was not taken by Fibonacci, and in Europe it took several more centuries until the triangle was finally rediscovered by Blaise Pascal in the seventeenth century.
Likewise, the Fibonacci numbers were not identified as anything special during the time Fibonacci wrote Liber Abaci in 1202. Centuries passed, and the numbers still went unnoticed. Then in the 1830s, C. F. Schimper and A. Braun noticed that the numbers appeared as the number of spirals of bracts on a pinecone (see figure 6.3).
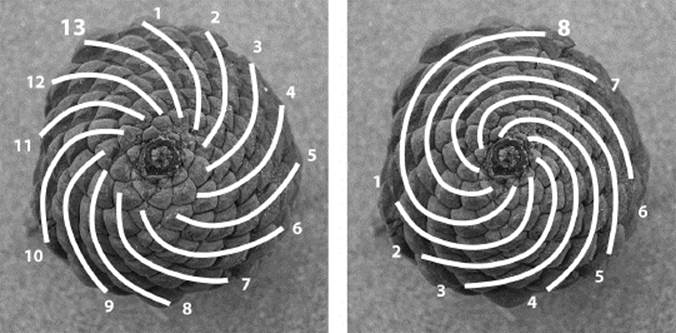
Figure 6.3: The number of spirals of a pinecone are Fibonacci numbers 8 and 13.
In the mid-1800s, the Fibonacci numbers began to capture the fascination of mathematicians. They took on their current name (Fibonacci numbers) from François-Édouard-Anatole Lucas (1842–1891), the French mathematician usually referred to as Edouard Lucas. Lucas is well known for his invention of mathematical recreations like the Tower of Hanoi puzzle, which appeared in 1883 under the name of N. Claus de Siam, which is an anagram of Lucas d'Amiens. His four-volume work on recreational mathematics (1882–1894) has become a classic. Lucas died as the result of a freak accident at a banquet when a plate was dropped and a piece flew up and cut his cheek. He died of erysipelas a few days later.
Lucas devised his own sequence by following the pattern set by Fibonacci. The Lucas numbers form a sequence of numbers much like the Fibonacci numbers, with which they share many properties. The Lucas numbers differ from the Fibonacci numbers in that they begin with different initial numbers:
L1 = 1, L2 = 3.
Ln = Ln–1 + Ln–2, for all natural numbers n greater than 2.
Hence, the sequence of Lucas numbers starts with
1, 3, 4, 7, 11, 18, 29…
At about this time, French mathematician Jacques-Philippe-Marie Binet (1786–1856) developed a formula for finding any Fibonacci number, given its position in the sequence. That is, with Binet's formula we can find the 118th Fibonacci number without having to list the previous 117 numbers. The Binet formula for the nth Fibonacci number is
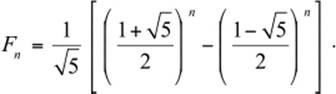
It should be noted that numerous other mathematicians prior to Binet came up with a formula analogous to this one; however, over time, the formula took on the name of Binet.
Today, these celebrated numbers still hold the fascination of mathematicians around the world. The Fibonacci Association was created in 1963 to provide enthusiasts an opportunity to share discoveries about these intriguing numbers and their applications. Through the Fibonacci Association's The Fibonacci Quarterly, many new facts, applications, and relationships about these numbers can be shared worldwide. According to its official website, The Fibonacci Quarterly is meant to serve as a focal point for interest in the Fibonacci numbers and related ideas, especially with respect to new results, research proposals, challenging problems, and innovative proofs of already-known relationships.
The Fibonacci numbers seem to crop up in countless botanical structures, such as the number of spirals of bracts on a pineapple or on a pinecone. They also appear when counting branches of various trees, and they make themselves omnipresent in architecture and art, as they are closely tied to the golden ratio. We recommend an excursion through these marvelous numbers, which can be found in The Fabulous Fibonacci Numbers by A. S. Posamentier and I. Lehmann (Amherst, NY: Prometheus Books, 2007). There you will find the enormous variety of appearances of the Fibonacci numbers.