Numbers: Their Tales, Types, and Treasures.

Chapter 5: Counting for Poets

6.3.MORE ABOUT THE PASCAL TRIANGLE

Let us now return to the Pascal triangle and explore some of its properties. This triangular arrangement provides us with a wealth of unusual, and quite amazing, relationships. For example, in any row where the second element (i.e., number) is a prime number, then every other number in that row will be a multiple of that prime number. For example in the eleventh row, the second number is 11, and therefore every other number in that row (55, 165, 330, 462) is a multiple of 11—of course with the exception of the 1s on either end of the row.

Another curious property of this triangular arrangement of numbers is shown in figure 6.4. Starting at the border, go down along one diagonal up to an arbitrary point. At the terminal point, look in the other direction, as indicated in figure 6.2, to see the number that will be the sum of the numbers that you passed through to get to that point. In figure 6.4, the circled numbers are the sum of the numbers in the shaded part of the diagonal.

A special case of this observation is that the numbers in the third diagonal are just the sums of the numbers in the second diagonal. As an example, consider the shaded part of the second diagonal in figure 6.5. It indicates the natural numbers from 1 to 7. The sum of these numbers may be found by simply looking to the number below and to the left of the number 7. It is 28 = 1 + 2 + 3 + 4 + 5 + 6 + 7.

The second diagonal is just the sequence of natural numbers. In section 4.5, we identified the triangular numbers as the sum of consecutive natural numbers beginning with 1. Hence, the third diagonal is the sequence of triangular numbers, marked in bold in figure 6.5.

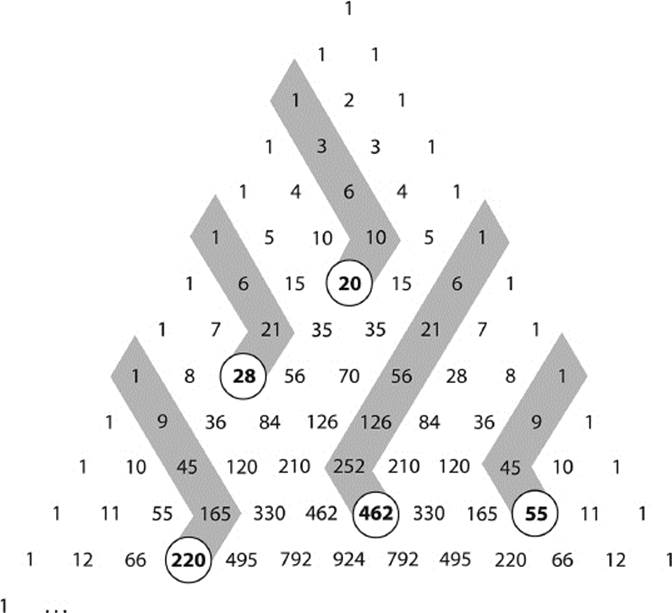
Figure 6.4

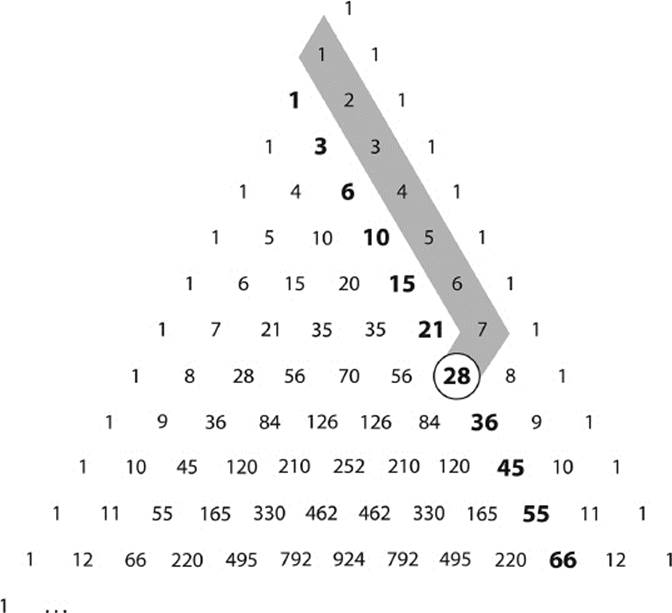
Figure 6.5: Triangular numbers in the Pascal triangle.

There are lots of interesting patterns to be found in the Pascal triangle. Consider the following in figure 6.6. Here we have marked the numbers encircling the number 10. Take the product of the numbers in circles, namely, 5 × 6 × 20 = 600, and then the product of the numbers in polygonal shapes, 4 × 10 × 15 = 600, and you will find a surprising result—the products are equal.

We can repeat this by considering similar shapes anywhere in the Pascal triangle. Figure 6.6 also shows two other examples: The numbers encircling 9 illustrate the products 1 × 8 × 45 = 360 and 1 × 10 × 36 = 360. Once again, notice that the two products are equal. Just to drive a point home, we will repeat this one more time with the shaded cells that encircle the number 210. Here the two products are 84 × 252 × 330 = 6,985,440 and 120 × 126 × 462 = 6,985,440.

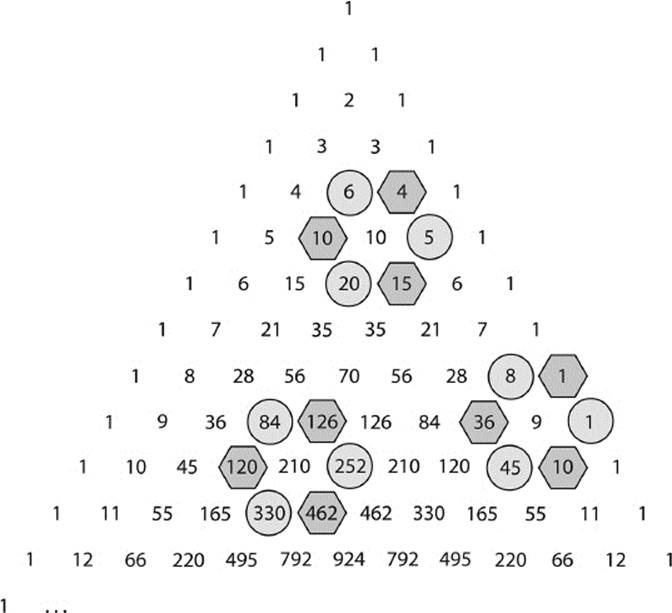
Figure 6.6: Patterns in the Pascal triangle.