Numbers: Their Tales, Types, and Treasures.

Chapter 9: Number Relationships

9.11.DIVISIBILITY OF NUMBERS

Number relationships can also manifest themselves in ways that assist us in making arithmetic judgments. In the base-10 number system, we are able to determine by inspection (and sometimes with a bit of simple arithmetic) when a given number is divisible by other numbers. For example, we know that when the last digit of a number is an even number, then the number is divisible by 2, such as with the numbers 30, 32, 34, 36, and 38. Of course, if the last digit is not divisible by 2, then we know that we cannot divide the number exactly by 2.

Divisibility by Powers of 2

Just as we look at the terminal digit on the number to determine if it is divisible by 2, so can we extend this to determine when a number is divisible by 4. In this case, when a number's last two digits (considered as a number) is divisible by 4, then, and only then, is the entire number also divisible by 4. For example, the underlined portion of each of the following numbers 124, 128, 356, and 768 is each divisible by 4, therefore, each of these numbers is also divisible by 4. On the other hand, the last two digits of the number 322, namely 22, is not divisible by 4, and therefore, the number 322 is not divisible by 4.

Furthermore, we can conclude that when, and only when, the last three digits of a number (considered as a number) is divisible by 8, the entire number also divisible by 8. A clever person would then extend this rule to a number whose last four digits form a number that is divisible by 16 to conclude that only then is the entire number divisible by 16, and so on for succeeding powers of 2.

Divisibility by Powers of 5

An analogous rule to that for powers of 2 can be used for divisibility by 5. We know that only when the last digit is either a 5 or a 0 is the number divisible by 5. Again, only when the last two digits (considered as a number) is divisible by 25 is the number divisible by 25. Some such examples of where the last two digits considered as number is divisible by 25 are 325, 450, 675, and 800, and each of these numbers is therefore divisible by 25 as well. This rule continues for powers of 5 (i.e., 5, 25, 125, 625, etc.) just as it did for powers of 2 earlier.

Divisibility by 3 and 9

A different rule is used to determine if a number is divisible by 3. Here we inspect the sum of the digits of the number. Only when the sum of the digits of the number being considered is divisible by 3 will the entire number be divisible by 3. For example, to determine if the number 345,678 is divisible by 3, we simply check to see if the sum of the digits 3 + 4 + 5 + 6 +7 + 8 = 33 is divisible by 3. In this case, it is; therefore, the number 345,678 is divisible by 3.

A similar rule can be used to determine divisibility by 9. If the sum of the digits of a given number is divisible by 9, then the number is divisible by 9. An illustration of this is the number 25,371, where the sum of the digits is 2 + 5 + 3 + 7 + 1 = 18, which is divisible by 9. Therefore, the number 25,371 is divisible by 9.

It is interesting to see why these rules work. Consider the number 25,371 and break it down as follows:

25,371 = 2 × (9,999 + 1) + 5 × (999 + 1)
+ 3 × (99 + 1) + 7 × (9 + 1) + 1.

Doing the indicated arithmetic operations, and some rearrangement, we get

= (2 × 9,999 + 5 × 999 + 3 × 99 + 7 × 9)
+ (2 + 5 + 3 +7 + 1)

We can see that the term (2 × 9,999 + 5 × 999 + 3 × 99 + 7 × 9) is a multiple of 9 (and a multiple of 3, as well). Therefore, we only need to have the remainder of the number, (2 + 5 + 3 + 7 + 1), to be a multiple of 9 (or 3)—which just happens to be the sum of the digits of the original number 825,372—in order for the entire number to be divisible by 9 (or 3). In this case, 2 + 5 + 3 + 7 + 1 = 18, which is divisible by 9 and 3. Hence the number 25,371 is divisible by 9 and 3.

For example, the number 789 is not divisible by 9, because 7 + 8 + 9 = 24, and 24 is not divisible by 9. Yet the number 789 is divisible by 3, since 24 is divisible by 3.

Divisibility by Composite Numbers

With the exception of 6 and 7, we have established divisibility rules to test for the numbers up to 10. Before we consider a test for divisibility by 7, we ought to make a statement about divisibility testing of composite (nonprime) numbers. To test divisibility by a composite number, we employ the divisibility tests for its “relatively-prime factors”—that is, numbers whose only common factor is 1. For example, the test for divisibility by the composite number 12 would require applying the divisibility test for 3 and 4, which are its relatively-prime factors (not 2 and 6, which are not relatively prime). The divisibility test for 18 requires applying the test for divisibility by 2 and for 9—which are relatively prime—and not the rules for divisibility by 3 and 6, whose product is also 18, but which are not relatively-prime factors, since they have a common factor of 3.

We can summarize the divisibility by composite numbers by inspecting the table below (table 9.9), which shows the first few composite numbers and their relatively-prime factors.

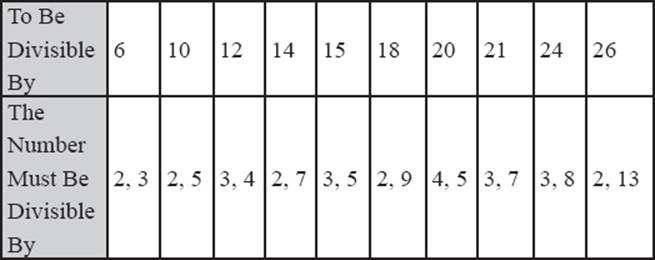
Table 9.9

The inclusion of some prime numbers in this chart now leads us to consider the divisibility rules for other prime numbers. We find the rules may be a bit cumbersome and not realistic for use in everyday-life situations—especially since the calculator is so pervasive. We will, therefore, present these divisibility rules largely for entertainment purposes, rather than as a useful tool.

The Rule for Divisibility by 7

Delete the last digit from the given number, and then subtract twice this deleted digit from the remaining number. If and only if the result is divisible by 7 will the original number be divisible by 7. This process may be repeated if the result is still too large for a simple visual inspection for divisibility by 7.

To better understand this divisibility test, we will apply it to determine if the number 876,547 is divisible by 7—without actually doing the division.

We begin with 876,547 and delete its units digit, 7, and then subtract its double, 14, from the remaining number: 87,654 – 14 = 87,640. Since we cannot yet visually determine if 87,640 is divisible by 7, we shall continue the process.

We take this resulting number 87,640 and delete its units digit, 0, and subtract its double, still 0, from the remaining number; we get 8,764 – 0 = 8,764.

This did not help us much in this case, so we shall continue the process. We delete its units digit, 4, from this resulting number, 8,764, and subtract its double, 8, from the remaining number to get 876 – 8 = 868. Since we still cannot visually inspect the resulting number, 868, for divisibility by 7, we will continue the process.

This time we delete its units digit, 8, from the resulting number 868 and subtract its double, 16, from the remaining number to get: 86 – 16 = 70, which we can easily determine is divisible by 7. Therefore, the original number, 876,547, is divisible by 7.

Now for the beauty of mathematics! That is, showing why this engaging procedure actually does what we say it does—test for divisibility by 7. Being able to show in a rather simple way why this procedure works contributes to what we call the wonders of mathematics.

Each step of the procedure actually amounts to a subtraction. For example, 8,764 will be reduced by subtracting 4 from the units and 2 × 4 = 8 from the tens. This reduces the original number by 84, which is a multiple of 7. The number 8,764 will become 8,764 – 84 = 8,680 = 868 × 10. This is divisible by 7 if and only if 868 is divisible by 7 (because 10 is not divisible by 7). Therefore, we can just ignore the 0 at the end, which explains why we can just “drop” the last digit. In each step, the process actually takes away “bundles of 7” from the original number. Whenever the remaining part is divisible by 7, then the original number is divisible by 7.

Table 9.10

To justify the technique of determining divisibility by 7, consider the various possible terminal digits (that you are “dropping”) and the corresponding subtraction that is actually being done in that step of the procedure. In table 9.10 you will see how the terminal digit together with its double in the tens place results in a number that is a multiple of 7. In all cases, the original number gets reduced by that multiple of 7, thereby changing the last digit of the original number to 0, which may then be dropped. If the remaining number is divisible by 7, then so is the original number divisible by 7.

The Rule for Divisibility by 11

Checking divisibility by 11 could be done in a similar manner as in the case of 7. But, since 11 is one more than the base (10), we have an even simpler test:

· Find the sums of the alternate digits and then take the difference of these two sums. If and only if that difference is divisible by 11 is the original number divisible by 11.

To better grasp this technique, consider, as an example, the number 246,863,727. First, we find the sums of the alternate digits: 2 + 6 + 6 + 7 + 7 = 28, and 4 + 8 + 3 + 2 = 17. The difference of these two sums is: 28 – 17 = 11, which is clearly divisible by 11. Therefore, the original number is divisible by 11.

This rule rests on the observation that each of the following numbers are divisible by 11:

To see how this rule for divisibility by 11 works, we shall break down the number 25,817 in the following way:

25,817 = 2 × 10⁴ + 5 × 10³ + 8 × 10² + 1 × 10¹ + 7 × 10⁰
= 2 × (10⁴ + 1 – 1) + 5 × (10³ + 1 – 1) + 8 × (10² + 1 – 1) + 1 × (10¹ + 1 – 1) + 7 × 1
= 2 × (10⁴ – 1) + 2 × 1 + 5 × (10³ + 1) – 5 × 1 + 8 × (10² – 1) + 8 × 1 + 1 × (10¹ + 1) – 1 × 1 + 7 × 1
= 2 × (10⁴ – 1) + 5 × (10³ + 1) + 8 × (10² – 1) + 1 × (10¹ + 1) + 2 – 5 + 8 – 1 + 7

Each of the bold terms are divisible by 11. Therefore, we need to just ensure that the sum of the rest of the terms is also divisible by 11. They are 2 – 5 + 8 – 1 + 7 = 11, which clearly is divisible by 11. Notice that this is the difference of the sums of the alternate digits, 2 – 5 + 8 – 1 + 7 = (2 + 8 + 7) – (5 + 1), of the number 25,817.

The Rule for Divisibility by 13

Delete the last digit from the given number, and then subtract nine times this deleted digit from the remaining number. If and only if the result is divisible by 13 will the original number be divisible by 13. Repeat this process if the result is too large for simple inspection of the divisibility by 13.

This is similar to the rule for testing divisibility by 7, except that the 7 is replaced by 13 and instead of subtracting twice the deleted digit, we subtract nine times the deleted digit each time. Let's check the number 5,616 for divisibility by 13. Begin with 5,616 and delete its units digit, 6, and subtract its multiple of 9, namely 54, from the remaining number: 561 – 54 = 507.

Since we still cannot visually inspect the resulting number for divisibility by 13, we continue the process.

Continue with the resulting number 507, and delete its units digit and subtract nine times this digit from the remaining number: 50 – 63 = –13, which is divisible by 13. Therefore, the original number is divisible by 13.

To determine the “multiplier,” 9, we sought the smallest multiple of 13 that ends in a 1. That was 91, where the tens digit is 9 times the units digit. Once again, consider the various possible terminal digits and the corresponding subtractions in the following table (table 9.11).

Table 9.11

In each case, a multiple of 13 is being subtracted one or more times from the original number. Hence, only if the remaining number is divisible by 13 will the original number be divisible by 13.

As we proceed to the divisibility test for the next prime, 17, we shall once again use this technique. We seek the multiple of 17 with a units digit of 1, that is, 51. This gives us the “multiplier” we need to establish the following rule.

The Rule for Divisibility by 17

Delete the units digit, and subtract five times the deleted digit each time from the remaining number until you reach a number small enough to determine if it is divisible by 17.

We can justify the rule for divisibility by 17 as we did the rules for 7 and 13. Each step of the procedure subtracts a “bunch of 17s” from the original number until we reduce the number to a manageable size and can make a visual inspection of divisibility by 17.

The patterns developed in the preceding three divisibility rules (for 7, 13, and 17) should lead you to develop similar rules for testing divisibility by larger primes. The following chart (table 9.12) presents the “multipliers” of the deleted digits for various primes.

Table 9.12

You may want to extend this chart; it can be fun, and challenging. In addition to extending the rules for divisibility by prime numbers, you may also want to extend your knowledge of divisibility rules to include composite (i.e., nonprime) numbers. Remember that to test divisibility for composite numbers we need to consider the rules for the number's relatively-prime factors—this guarantees that we will be using independent divisibility rules. These rules for divisibility should enhance your appreciation for the relationship of numbers in a mathematical context.

At this point we have presented a rather exhaustive illustration of how numbers can relate to one another. Many of these illustrations are unexpected and, therefore, that much more appreciated. We hope to have motivated readers to seek out other illustrations of number relationships.