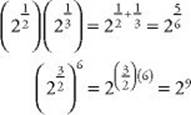SAT SUBJECT TEST MATH LEVEL 1
TOPICS IN ARITHMETIC
CHAPTER 2
Basic Arithmetic
SQUARES AND SQUARE ROOTS
The exponent that appears most often on the Math 1 test is 2. Although a2 can be read “a to the second,” it is usually read “a squared.” You will see 2 as an exponent in many formulas. For example:
• A = s 2 (the area of a square)
• A = πr 2 (the area of a circle)
• a2 + b2 = c 2 (the Pythagorean theorem)
• x2 - y 2 = (x - y)(x + y) (factoring the difference of two squares)
Numbers that are the squares of integers are called perfect squares. You should recognize at least the squares of the integers from 0 through 15.
Of course if you need to evaluate 132, you can use your calculator. However, it is often helpful to recognize these perfect squares. That way, if you see 169, you will immediately think “that is 132.”
Two numbers, 5 and –5, satisfy the equation x2 = 25. The positive one, 5, is called the square root of 25 and is denoted by the symbol 
. Clearly, each perfect square has a square root: 
, 
, 
, and 
. However, it is an important fact that every positive numberhas a square root.
Key Fact A12
For any positive number a, there is a positive number b that satisfies the equation b2= a. That number, b, is called the square root of a and is written 
. So, for any positive number a, 
.
Key Fact A13
For any positive numbers a and b:
For example, 
and 
.
Don”t Get Confused
• 
For example:
• 
• 
• 
The expression a3 is often read “a cubed.” Numbers that are the cubes of integers are called perfect cubes. You should memorize the perfect cubes in the following table.
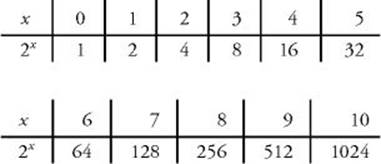
The only other powers you should recognize immediately are the powers of 2 up to 210.
In the same way that we write 
to indicate that b2 = a:
• We write 
to indicate that b3 = a and call b the cube root of a.
• We write 
to indicate that b4 = a and call b the fourth root of a.
• For any integer n 
2, we write 
to indicate that bn = a and call b the nth root of a.
For example:
• 
because 53 = 125.
• 
because (–2)3 = –8.
• 
because 210 = 1024.
Note that 
is undefined because there is no real number x such that x 2 = –64. If you enter on your calculator, you will get an error message. (In Chapter 17, you will read about the imaginary unit i and will review the fact that 
is 8i.)
Key Fact A14
For any real number a and integer n 
2:
• If n is odd, then 
is the unique real number x that satisfies the equation xn= a.
• If n is even and a is positive, then is the unique positive number x that satisfies the equation xn= a.
We can now expand our definition of exponents to include fractions.
Key Fact A15
For any positive number b and positive integers n and m with n 2:
• 
• 
For example:
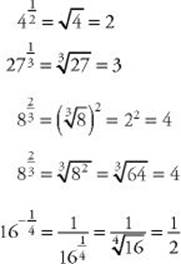
The laws of exponents, listed in KEY FACT A11, are equally valid if any of the exponents are fractions. For example:
