SAT SUBJECT TEST MATH LEVEL 1

TOPICS IN ARITHMETIC

CHAPTER 2
Basic Arithmetic

LOGARITHMS

Recall that the statement 2⁴ = 16 is usually read as “2 to the 4th power equals 16.” Another way to read this stresses the role of the exponent 4: “4 is the exponent to which the base 2 must be raised to equal 16.” Mathematicians have a special word for this exponent—logarithm. The statement 2⁴ = 16 is equivalent to the statement log₂ 16 = 4, which is read, “the base 2 logarithm of 16 is 4.”

TIP

A logarithm is an exponent.

Key Fact A16

If b is a positive number not equal to 1 and x > 0,

log_bx = y if and only if b ^y = x.

For example:

• log₁₀100 = 2 because 10² = 100

• because

• because

Although you can always estimate the value of a logarithm, in general there is no easy way to evaluate a logarithm exactly without a calculator. For example, log₁₀ 5 is the number x such that 10^x= 5. Since 10⁰ = 1 and 10¹ = 10, you know that 0 < log₁₀5 < 1. You could improve your estimate by noting that since , which is only slightly greater than 3, , and so 0.5 < x < 1. The LOG button on your calculator evaluates base 10 logarithms. So you can use your calculator to get that log₁₀ 5 = LOG 5 = 0.699.

What if you want to know the value of log₂ 5? Clearly, you cannot just enter LOG 5 on your calculator since that means log₁₀ 5. Also, since 2² = 4, log₂ 4 = 2 and so log₂ 5 > 2, certainly not 0.699. The following KEY FACT shows you how to use your calculator to evaluate log₂ 5 exactly.

TIP

The LOG button on your calculator evaluates only base 10 logarithms. So LOG 5 = 0.699 means log₁₀ 5 = 0.699, which is often written log 5, without the base being indicated.

Key Fact A17

CHANGE OF BASE FORMULA

Similarly, 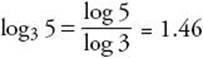and .

Reminder: In the line above, log 5 and log 3 are abbreviations for log₁₀5 and log₁₀3, respectively.

You need to know a few important laws of logarithms. They are all direct consequences of the laws of exponents (KEY FACT A11).

Key Fact A18

LAWS OF LOGARITHMS

For any positive base b 1 and any positive numbers x, y, and n:

• log_b(xy) = log_b x + log_b y

•

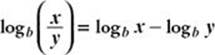
• log_bxⁿ= n log_b x

• log_b bⁿ= n (In particular, log_b 1 = log_b b⁰ = 0 and log_b b = log_b b¹= 1)

For example, if log_b 2 = x and log_b 3 = y, then:

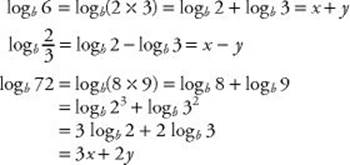
As you will see in Chapter 6, the third rule in KEY FACT A17 allows you to solve equations in which the variable is an exponent by bringing the variable down to the base line. To solve the equation 2^x = 512, for example, take the logarithm of both sides: log_b 2^x = log_b 512. Then

Note that what you choose for the base b does not matter. As a consequence, you might as well let b = 10. Therefore, . Now use your calculator:

x = (log 512) (log 2) = 9