SAT SUBJECT TEST MATH LEVEL 1
TOPICS IN ARITHMETIC
![]()
CHAPTER 4 Ratios and Proportions
![]()
• Ratios
• Proportions
• Exercises
• Answers Explained
A ratio is a fraction that compares two quantities that are measured in the same units. The first quantity is the numerator, and the second quantity is the denominator.
RATIOS
For example, if in right ![]() ABC, the length of leg
ABC, the length of leg ![]() is 6 inches and the length of leg
is 6 inches and the length of leg ![]() is 8 inches, we say that the ratio of AC to BC is 6 to 8, which is often written as 6 : 8 but is just the fraction
is 8 inches, we say that the ratio of AC to BC is 6 to 8, which is often written as 6 : 8 but is just the fraction ![]() . Like any fraction, a ratio can be reduced and can be converted to a decimal or a percent.
. Like any fraction, a ratio can be reduced and can be converted to a decimal or a percent.
TIP 
Ratios can always be written as a fraction.
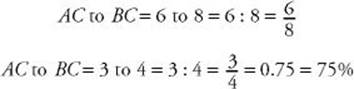
If you know that AC = 6 inches and BC = 8 inches, you know that the ratio of AC to BC is 6 to 8. However, if you know that the ratio of AC to BC is 6 to 8, you cannot determine how long either side is. They may be 6 and 8 inches long but not necessarily. Their lengths, in inches, may be 60 and 80 or 300 and 400 since ![]() and
and ![]() are both equivalent to the ratio
are both equivalent to the ratio ![]() . In fact, there are infinitely many possibilities for the lengths.
. In fact, there are infinitely many possibilities for the lengths.

The important thing to observe is that the length of ![]() can be any multiple of 3 as long as the length of
can be any multiple of 3 as long as the length of ![]() is the same multiple of 4.
is the same multiple of 4.
Key Fact C1
If two numbers are in the ratio of a : b, then for some number x, the first number is ax and the second number is bx.
|
TACTIC |
In any ratio problem, write x after each number and use some given information to solve for x. |
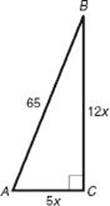
EXAMPLE 1: In a right triangle, the ratio of the length of the shorter leg to the length of the longer leg is 5 to 12. If the length of the hypotenuse is 65, what is the perimeter of the triangle?
Draw a right triangle and label it with the given information; then use the Pythagorean theorem.
![]()
So AC = 5(5) = 25, BC = 12(5) = 60, and the perimeter equals 25 + 60 + 65 = 150.
Ratios can be extended to 3 or 4 or more terms. For example, we can say that the ratio of freshmen to sophomores to juniors to seniors in a school band is 3 : 4 : 5 : 4. This means that for every 3 freshmen in the band there are 4 sophomores, 5 juniors, and 4 seniors.
Note
TACTIC C1 applies to extended ratios as well.
EXAMPLE 2: What is the degree measure of the largest angle of a quadrilateral if the measures of the four angles are in the ratio of 2 : 3 : 3 : 4?
Let the measures of the four angles be 2x, 3x, 3x, and 4x. Use the fact that the sum of the measures of the angles in any quadrilateral is 360°.
2x + 3x + 3x + 4x = 360 ![]() 12x = 360
12x = 360 ![]() x = 30
x = 30
The measure of the largest angle is 4(30) = 120°.