SAT SUBJECT TEST MATH LEVEL 1
PLANE GEOMETRY
CHAPTER 9 Triangles
RIGHT TRIANGLES
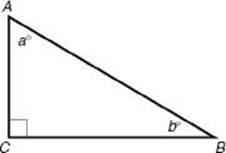
If a and b are the measures in degrees, of the acute angles of a right triangle, then by KEY FACT H1, 90 + a + b = 180 
a + b = 90.
Key Fact H4
In any right triangle, the sum of the measures of the two acute angles is 90º.
EXAMPLE 3: To find the average of a and b in 
below, note that by KEY FACT H4, a + b = 90, so 
.
The most important fact concerning right triangles is the Pythagorean theorem, which is given in the first line of KEY FACT H5. The second and third lines of KEY FACT H5 are important corollaries of the Pythagorean theorem.
Key Fact H5
PYTHAGOREAN THEOREM AND COROLLARIES
Let a, b, and c be the lengths of the sides of 
, with a 
b 
c.
• a2+ b2= c2 if and only if angle C is a right angle.
• a2+ b2< c2 if and only if angle C is obtuse.
• a2+ b2> c2, if and only if angle C is acute.
TIP 
The Pythagorean theorem is probably the most important theorem you need to know. Be sure to review all of its uses.
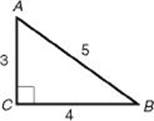
32 + 42 = 52
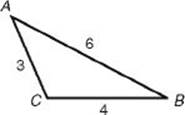
32 + 42 < 62
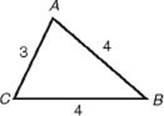
32 + 42 > 42
EXAMPLE 4: Since 82 + 152 = 64 + 225 = 289 = 172, a triangle whose sides have lengths 8, 15, and 17 is a right triangle. Since 102 + 152 = 100 + 225 = 325 < 192, a triangle whose sides have lengths 10, 15, and 19 is not a right triangle-it is obtuse.
On the Math 1 test, the most common right triangles whose sides are integers are the 3-4-5 right triangle and its multiples.
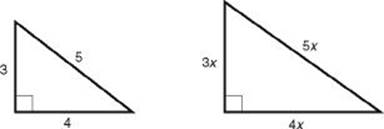
Key Fact H6
For any positive number x, there is a right triangle whose sides are 3x, 4x, 5x.
For example:
|
x = 1 |
3, 4, 5 |
|
x = 2 |
6, 8, 10 |
|
x = 3 |
9, 12, 15 |
|
x = 4 |
12, 16, 20 |
|
x = 5 |
15, 20, 25 |
|
x = 10 |
30, 40, 50 |
|
x = 50 |
150, 200, 250 |
|
x = 100 |
300, 400, 500 |
Other right triangles with integer sides that you should recognize immediately are the ones whose sides are 5, 12, 13 and 8, 15, 17.
NOTE
KEY FACT H6 applies even if x is not an integer. For example:
x = 0.5 1.5, 2, 2.5
x = π 3π, 4π, 5π