Exercises

SAT SUBJECT TEST MATH LEVEL 1

PLANE GEOMETRY

CHAPTER 9 Triangles

1. In ΔABC, the measures of the exterior angles at vertices A and B are 145° and 125°, respectively. Which of the following statements about ΔABC must be true?

I. The triangle is a right triangle.

II. The triangle is an isosceles triangle.

III. The triangle is a scalene triangle.

(A) None

(B) I only

(D) I and II only

(E) I and III only

2. In the triangle below, what is the value of x?

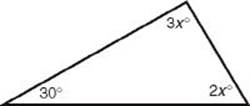
(A) 20

(B) 30

(D) 50

(E) 60

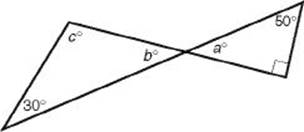
3. In the figure below, what is the value of c ?

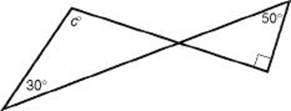
(A) 100

(B) 110

(D) 130

(E) 140

4. The lengths of two sides of a right triangle are 15 and 17. Which of the following could be the length of the third side?

I. 8

II. 19

III.

(A) I only

(B) II only

(D) I and III

(E) I, II, and III

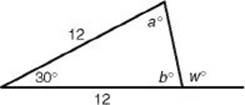
5. What is the value of w in the figure below?

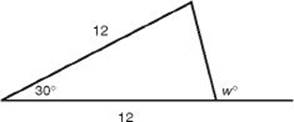
(A) 60

(B) 90

(D) 120

(E) 150

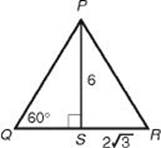
6. What is the area of an equilateral triangle whose altitude is 6?

(A) 18

(B) 12

(D) 36

(E) 24

7. Which of the following expresses a true relationship between x and y in the figure below?

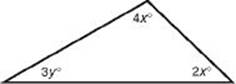
(A) y = 60 – 2x

(B) y = 2x

(D) y = 180 – 3x

(E) x = 90 – 3y

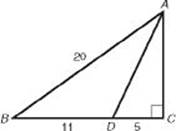
8. What is the value of AD in the triangle below?

(A) 5

(B) 10

(D) 13

(E) 12

Questions 9 and 10 refer to the following figure.

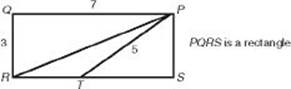
9. What is the area of ΔPRT?

(A) 3

(B) 4.5

(D) 7.5

(E) 10

10. What is the perimeter of ΔPRT?

(A) 8 +

(B) 8 +

(D) 17

(E) 18

11. If the measures of the angles of a triangle are in the ratio of 1 : 2 : 3, what is the ratio of the length of the smallest side of the triangle to the length of the longest side of the triangle?

(A) 1 : 2

(B) 1 : 3

(D) 2 : 3

(E) 2 : 5

12. If the difference between the measures of the two acute angles of a right triangle is 20°, what is the measure, in degrees, of the smaller one?

(A) 20°

(B) 35°

(D) 55°

(E) 80°

13. If one side of ΔABC is 5, what is the smallest integer that could be the perimeter of the triangle?

(A) 8

(B) 10

(D) 12

(E) 15

14. In the figure below, what is the length of ?

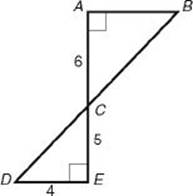
(A) 14.00

(B) 14.09

(D) 15.62

(E) 16.00

15. The lengths of the sides of a triangle are 3, 5, and x. How many possible values of x are there, if x must be an integer?

(A) 1

(B) 5

(D) 8

(E) Infinitely many

ANSWERS EXPLAINED

Answer Key

1. (E)	6. (B)	11. (A)
2. (B)	7. (A)	12. (B)
3. (B)	8. (D)	13. (C)
4. (D)	9. (B)	14. (B)
5. (C)	10. (B)	15. (B)

Solutions

Each of the problems in this set of exercises is typical of a question you could see on a Math 1 test. When you take the model tests in this book and, in particular, when you take the actual Math 1 test, if you get stuck on questions such as these, you do not have to leave them out—you can almost always answer them by using one or more of the strategies discussed in the “Tactics” chapter. The solutions given here do not depend on those strategies; they are the correct mathematical ones.

See Important Tactics for an explanation of the symbol ⇒, which is used in several answer explanations.

1. (E) First, draw ΔABC.

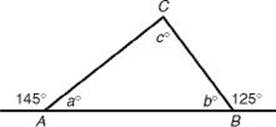
By KEY FACT G2, a + 145 = 180 and . Then by KEY FACT H1, (I is true). Since the measures of all three angles are different, by KEY FACT H3, the lengths of all three sides are different (II is false and III is true). Only I and III are true.

2. (B)

3. (B) In the figure below, . Since vertical angles are congruent, b = 40. So 40 + 30 + C = 180 ⇒ C = 110.

4. (D) If the triangle were not required to be right, by KEY FACT H9 any number greater than 2 and less than 32 could be the length of the third side. For a right triangle, though, there are only two possibilities:

• 17 is the length of the hypotenuse, and the legs have lengths 15 and 8. I is true. (If you did not recognize the 8-15-17 triangle, use the Pythagorean theorem: solve the equation 15² + x²= 17².)

• 15 and 17 are the lengths of the two legs. Use the Pythagorean theorem to find the hypotenuse:

. III is true.

• Since , a 15-17-19 triangle is not a right triangle. II is false. Only I and III are true.

5. (C) Since the triangle is isosceles, in the figure below, a and b are equal. Since a + b + 30 = 180, a and b are each 75. Finally, w = 180 – 75 = 105.

6. (B) Draw altitude in equilateral ΔPQR. By KEY FACT H8, . Since, in ΔPQR, SR is one-half the base, the area of the triangle is .

7. (A)

8. (D) Use the Pythagorean theorem twice, unless you recognize the common right triangles in this figure (which you should). Since AB = 20 and BC = 16, ΔABC is a 3x-4x-5x right triangle with x = 4. So AC = 12, and ΔACD is a right triangle whose legs are 5 and 12. Its hypotenuse, AD, is therefore 13.

9. (B) Since ΔPST is a right triangle whose hypotenuse is 5 and one of whose legs is 3, the other leg, , is 4. Since SR = PQ = 7, TR = 3. Now, ΔPRT has a base of 3 () and a height of 3 (), and so its area is .

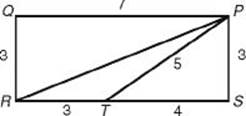
10. (B) In ΔPRT, we already have that PT = 5 and TR = 3; we need only find PR, which is the hypotenuse of ΔPQR. By the Pythagorean theorem:

So the perimeter is .

11. (A) If the measures of the three angles are in the ratio of 1 : 2 : 3, then for some number x, their values are x, 2x, and 3x.

So the triangle is a 30-60-90 right triangle, and for some number a, the lengths of the sides are a, a, and 2a. The ratio of the length of the smallest side to the length of the largest side is a : 2a = 1 : 2.

12. (B) Draw a picture, label it, and then write the equations:

a + b = 90 and a – b = 20

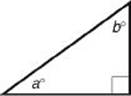
By adding the equations, we get 2a = 110. So a = 55 and b = 90 – 55 = 35. The measure of the smallest angle is 35°.

13. (C) If x and y are the lengths of the other two sides, then by KEY FACT H9, . So the smallest integer that the perimeter could be is 11. (In fact, there is an isosceles triangle whose sides are 3, 3, and 5.)

14. (B) The two vertical angles at C are congruent and since they are both right angles. Therefore, by KEY FACT H13, ΔCAB and ΔCED are similar. So their sides are in proportion, with a ratio of similitude of . By the Pythagorean theorem, (CD)² = 4² + 5² = 16 + 25 = 41. So . . Finally, .

15. (B) By the triangle inequality (KEY FACT H9),

So there are 5 possible integer values of x: 3, 4, 5, 6, 7.