SAT SUBJECT TEST MATH LEVEL 2
PART 2
REVIEW OF MAJOR TOPICS
CHAPTER 1
Functions
1.1 Overview
INVERSES
The inverse of a function f, denoted by f –1, is a relation that has the property that f(x) 
f –1(x) = f –1(x) f(x) = x. The inverse of a function is not necessarily a function.
EXAMPLES
1. 
the inverse of f ?
To answer this question assume that 
and verify that f(x) f –1(x) = x.
To verify this, proceed as follows:
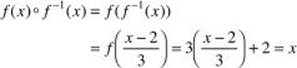
and
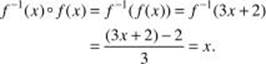
Since 
is the inverse of f.
2. f = {(1,2),(2,3),(3,2)}. Find the inverse.
f −1 ={(2,1), (3,2), (2,3)}
|
TIP Remember that the inverse of a function need not be a function. |
To verify this, check f f –1 and f –1 f term by term.
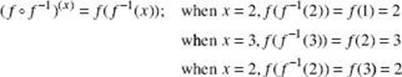
Thus, for each x, f(f –1(x)) = x.
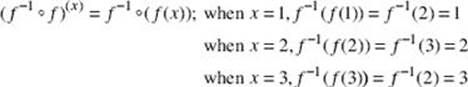
Thus, for each x, f –1(f(x)) = x. In this case f –1 is not a function.
If the point with coordinates (a,b) belongs to a function f, then the point with coordinates (b,a) belongs to the inverse of f. Because this is true of a function and its inverse, the graph of the inverse is the reflection of the graph of f about the line y = x.
3. f –1 is not a function.
|
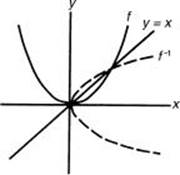
TIP Graphs of inverses are reflections about the line y = x. |
4. f –1 is a function.
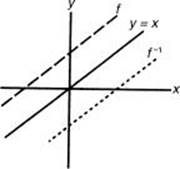
As can be seen from the above examples, the graph of an inverse is the reflection of the graph of a function (or relation) through the line y = x. Algebraically, the equation of an inverse of a function can be found by replacing f (x) by y; interchanging x and y; and solving the resulting equation for y.
5. f(x) = 3x + 2. Find f −1.
In order to find f –1, interchange x and y and solve for y: x = 3y + 2, which becomes 
.
Thus,
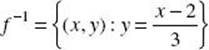
6. f(x) = x2. Find f −1.
Write y = x2
Interchange x and y: x = y2.
Solve for 
Thus, the inverse of y = x2 is not a function.
The inverse of any function f can always be made a function by limiting the domain of f. In Example 6 the domain of f could be limited to all nonnegative numbers or all nonpositive numbers. In this way f –1 would become either 
or 
, both of which are functions.
7. f(x) = x2 and x ≥ 0. Find f −1.
Write y = x2 and x ≥ 0. Then switch x and y: x = y2 and y ≥ 0.
Solve for y: 
.
Here f −1 is the function 
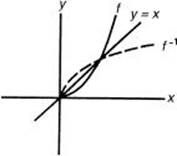
Finding an equation for the inverse of a function can also be used to determine the range of a function, as shown in the following example.
8. Find the range of 
.
First replace f(x) by y, and interchange x and y to get 
. Then solve for y:
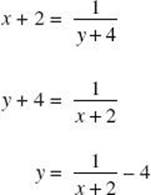
In order for this to be defined, x ≠ −2. In other words, −2 is not in the range of f. (This could also be determined by observing that 
in the original function can never be zero.)
EXERCISES
1. If f(x) = 2x – 3, the inverse of f, f –1, could be represented by
(A) f –1(x) = 3x − 2
(B) 
(C) 
(D) 
(E) 
2. If f(x) = x , the inverse of f, f –1, could be represented by
(A) 
(B) 
(C) 
(D) 
(E) f –1 does not exist
3. The inverse of f = {(1,2),(2,3),(3,4),(4,1),(5,2)} would be a function if the domain of f is limited to
(A) {1,3,5}
(B) {1,2,3,4}
(C) {1,5}
(D) {1,2,4,5}
(E) {1,2,3,4,5}
4. Which of the following could represent the equation of the inverse of the graph in the figure?
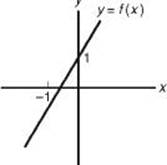
(A) y = –2x + 1
(B) y = 2x + 1
(C) 
(D) 
(E) 