AP Physics C Exam

Part IV

Content Review for the AP Physics C Exam

Chapter 11 Electric Forces and Fields

ELECTRIC CHARGE

The basic components of atoms are protons, neutrons, and electrons. Protons and neutrons form the nucleus (and are referred to collectively as nucleons), while the electrons keep their distance, swarming around the nucleus. Most of an atom consists of empty space. In fact, if a nucleus were the size of the period at the end of this sentence, then the electrons would be 5 meters away. So what holds such an apparently tenuous structure together? One of the most powerful forces in nature: the electromagnetic force. Protons and electrons have a quality called electric chargethat gives them an attractive force. Electric charge comes in two varieties; positive and negative. A positive particle always attracts a negative particle, and particles of the same charge always repel each other. Protons are positively charged, and electrons are negatively charged.

Protons and electrons are intrinsically charged, but bulk matter is not. This is because the amount of charge on a proton exactly balances the charge on an electron, which is quite remarkable in light of the fact that protons and electrons are very different particles. Since most atoms contain an equal number of protons and electrons, their overall electric charge is 0, because the negative charges cancel out the positive charges. Therefore, in order for matter to be charged, an imbalance between the numbers of protons and electrons must exist. This can be accomplished by either the removal or addition of electrons (that is, by the ionization of some of the object’s atoms). If you remove electrons, then the object becomes positively charged, while if you add electrons, then it becomes negatively charged. Furthermore, charge is conserved. For example, if you rub a glass rod with a piece of silk, then the silk will acquire a negative charge and the glass will be left with an equal positive charge. Net charge cannot be created or destroyed. (Charge can be created or destroyed—it happens all the time—but net charge cannot.)

The magnitude of charge on an electron (and therefore on a proton) is denoted e. This stands for elementary charge, because it’s the basic unit of electric charge. The charge of an ionized atom must be a whole number times e, because charge can be added or subtracted only in lumps of size e. For this reason we say that charge is quantized. To remind us of the quantized nature of electric charge, the charge of a particle (or object) is denoted by the letter q. In the SI system of units, charge is expressed in coulombs (abbreviated C). One coulomb is a tremendous amount of charge; the value of e is about 1.6 × 10^–19 C.

COULOMB’S LAW

The electric force between two charged particles obeys a law that is very similar to that describing the gravitational force between two masses: they are both inverse-square laws. The electric force between two particles with charges of q₁ and q₂, separated by a distance r, is given by the equation

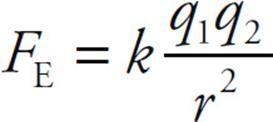
This is Coulomb’s Law. We interpret a negative F_E as an attraction between the charges and a positive F_E as a repulsion. The value of the proportionality constant, k, depends on the material between the charged particles. In empty space (vacuum)—or air, for all practical purposes—it is called Coulomb’s constant and has the approximate value k = 9 × 10⁹ N · m²/C². For reasons that will become clear later in this chapter, k is usually written in terms of a fundamental constant known as the permittivity of free space, denoted ε₀, whose numerical value is approximately 8.85 × 10^–12 C²/N · m². The equation that gives k in terms of ε₀ is:

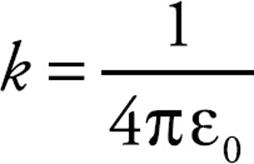
Coulomb’s Law for the force between two point charges is then written as

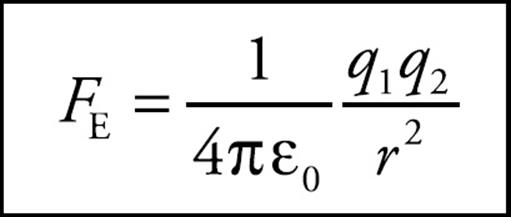
Let’s compare the electric force to the gravitational force between two protons, a distance r apart.

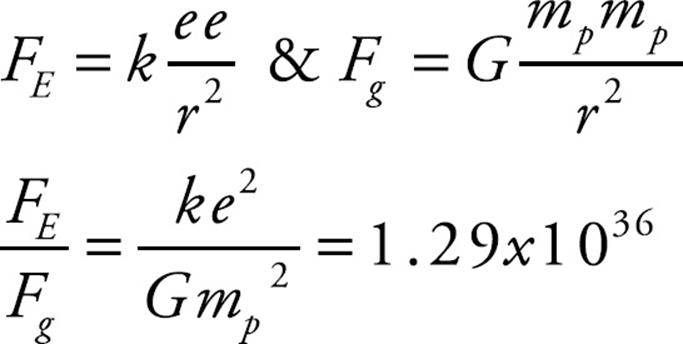
Example 1 Consider two small spheres, one carrying a charge of +1.5 nC and the other a charge of –2.0 nC, separated by a distance of 1.5 cm. Find the electric force between them. (“n” is the abbreviation for “nano,” which means 10^–9.)

Solution. The electric force between the spheres is given by Coulomb’s Law:

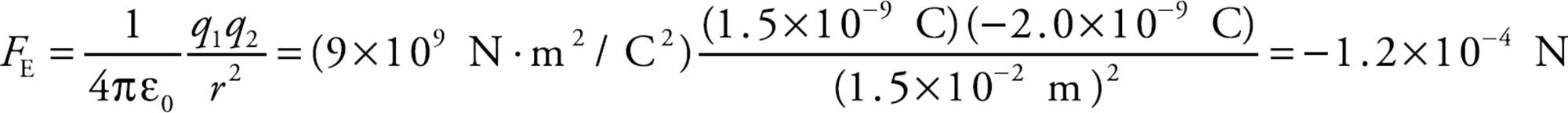
The fact that F_E is negative means that the force is one of attraction, which we naturally expect, since one charge is positive and the other is negative. The force between the spheres is along the line that joins the charges, as we’ve illustrated below. The two forces shown form an action/reaction pair.

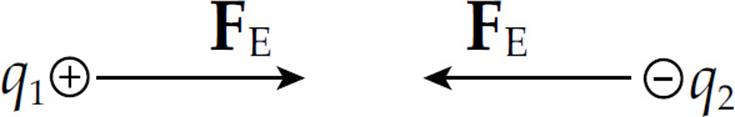
Superposition

Consider three point charges: q₁, q₂, and q₃. The total electric force acting on, say, q₂ is simply the sum of F_1-on-2, the electric force on q₂ due to q₁, and F_3-on-2, the electric force on q₂ due to q₃:

F_{on 2} = F_1-on-2 + F_3-on-2

The fact that electric forces can be added in this way is known as superposition.

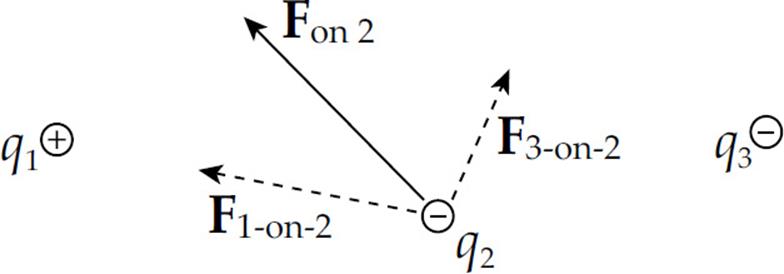
Example 2 Consider four equal, positive point charges that are situated at the vertices of a square. Find the net electric force on a negative point charge placed at the square’s center.

Solution. Refer to the diagram on the next page. The attractive forces due to the two charges on each diagonal cancel out: F₁ + F₃ = 0, and F₂ + F₄ = 0, because the distances between the negative charge and the positive charges are all the same and the positive charges are all equivalent. Therefore, by symmetry, the net force on the center charge is zero.

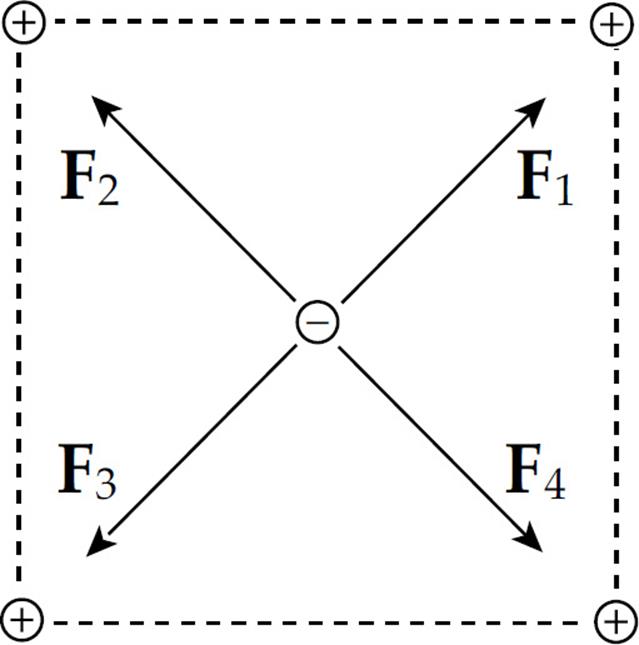
Example 3 If the two positive charges on the bottom side of the square in the previous example were removed, what would be the net electric force on the negative charge? Assume that each side of the square is 4.0 cm, each positive charge is 1.5 µC, and the negative charge is –6.2 nC. (µ is the symbol for “micro-,” which equals 10^–6.)

Solution. If we break down F₁ and F₂ into horizontal and vertical components, then by symmetry the two horizontal components will cancel each other out, and the two vertical components will add:

Since the diagram on the left shows the components of F₁ and F₂ making a right triangle with legs each of length 2 cm, it must be that F_1y = F₁ sin 45° and F_2y = F₂ sin 45°. Also, the magnitude of F₁ equals that of F₂. So the net electric force on the negative charge is F_1y + F_2y = 2F sin 45°, where F is the strength of the force between the negative charge and each of the positive charges. 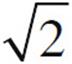If s is the length of each side of the square, then the distance r between each positive charge and the negative charge is r = s and

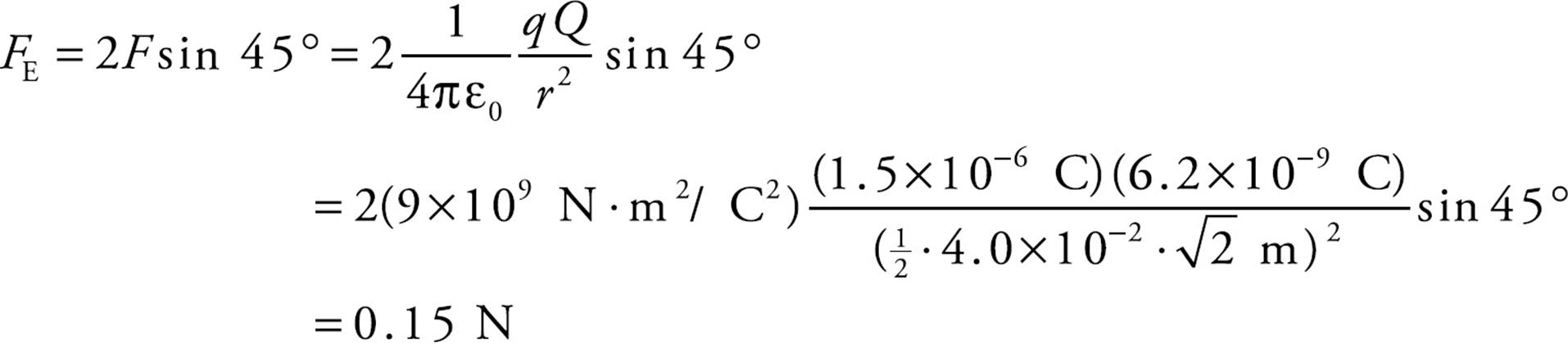
The direction of the net force is straight upward, toward the center of the line that joins the two positive charges.

Example 4 Two pith balls of mass m are each given a charge of +q. They are hung side-by-side from two threads each of length L, and move apart as a result of their electrical repulsion. Find the equilibrium separation distance x in terms of m, q, and L. (Use the fact that if θ is small, then tan θ ≈ sin θ.)

Solution. Three forces act on each ball: weight, tension, and electrical repulsion:

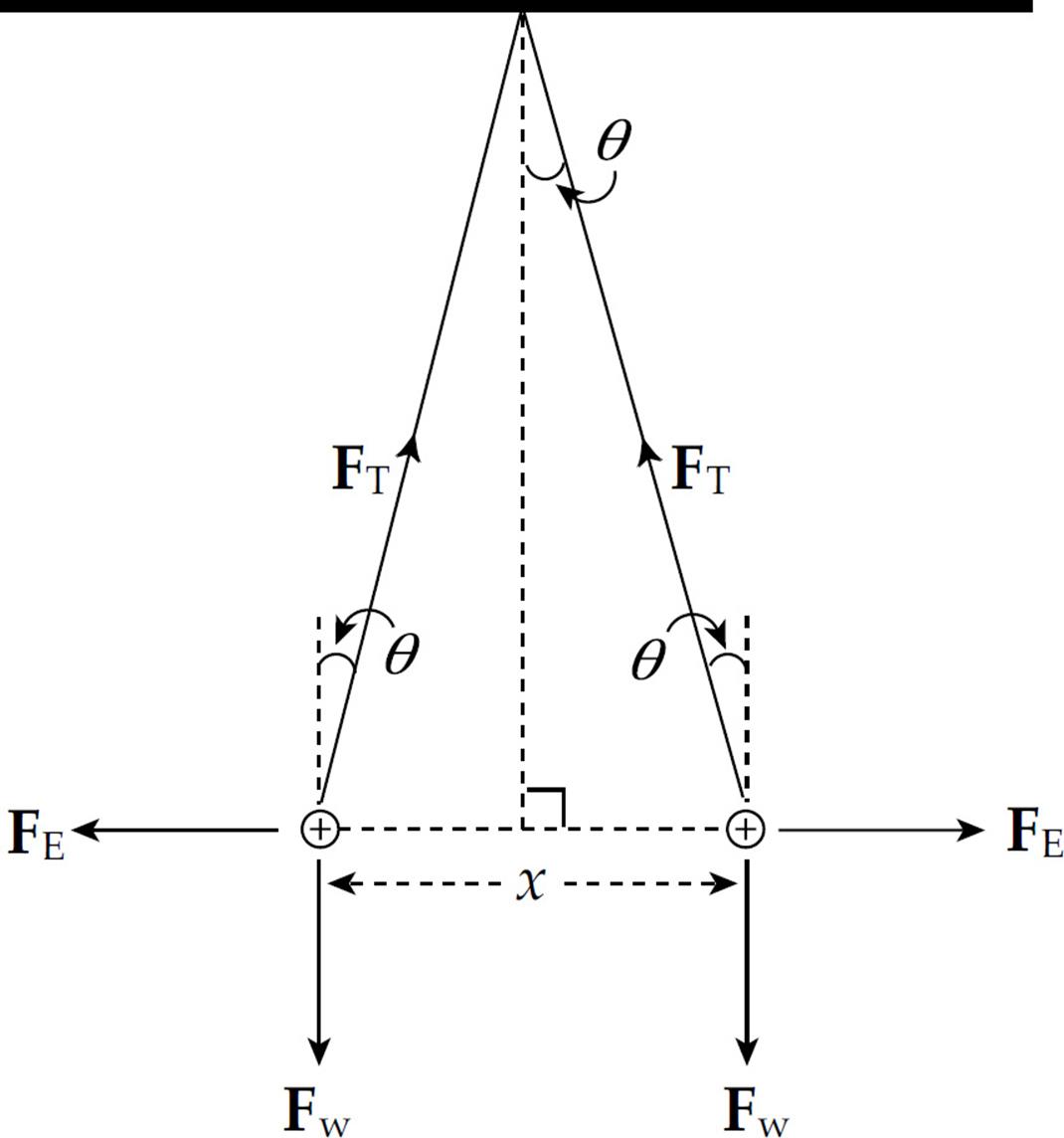
When the balls are in equilibrium, the net force each feels is zero. Therefore, the vertical component of F_T must cancel out F_w and the horizontal component of F_T must cancel out F_E:

F_T cos θ = F_w and F_T sin θ = F_E

Dividing the second equation by the first, we get tan θ = F_E/F_w. Therefore,

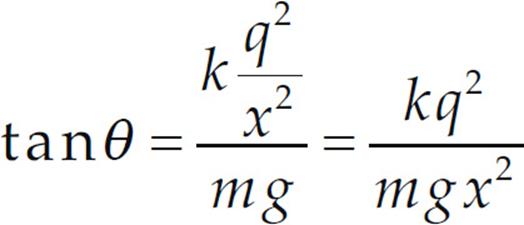
Now, to approximate: If θ is small, the tan θ ≈ sin θ and, from the diagram sin θ = x/L. Therefore, the equation above becomes

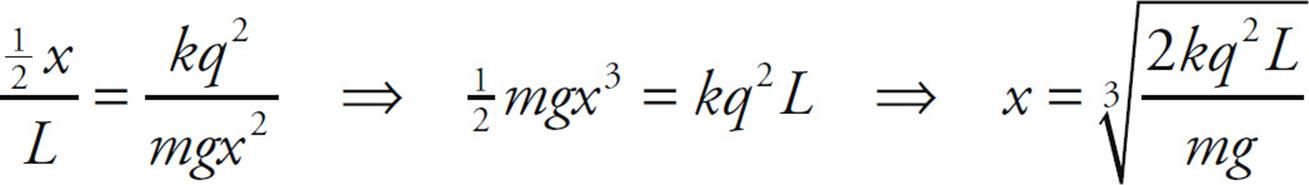
THE ELECTRIC FIELD

The presence of a massive body such as Earth causes objects to experience a gravitational force directed toward Earth’s center. For objects located outside Earth, this force varies inversely with the square of the distance and directly with the mass of the gravitational source. A vector diagram of the gravitational field surrounding Earth looks like this:

We can think of the space surrounding Earth as permeated by a gravitational field that’s created by Earth. Any mass that’s placed in this field then experiences a gravitational force due to this field.

The same process is used to describe the electric force. Rather than having two charges reach out across empty space to each other to produce a force, we can instead interpret the interaction in the following way: The presence of a charge creates an electric field in the space that surrounds it. Another charge placed in the field created by the first will experience a force due to the field.

Consider a point charge Q in a fixed position and assume that it’s positive. Now imagine moving a tiny positive test charge q around to various locations near Q. At each location, measure the force that the test charge experiences, and call it F. Divide this force by the test charge q; the resulting vector is the electric field vector, E, at that location:

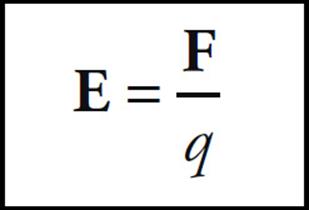
The reason for dividing by the test charge is simple. If we were to use a different test charge with, say, twice the charge of the first one, then each of the forces F we’d measure would be twice as much as before. But when we divided this new, stronger force by the new, greater test charge, the factors of 2 would cancel, leaving the same ratio as before. So this ratio tells us the intrinsic strength of the field due to the source charge, independent of whatever test charge we may use to measure it.

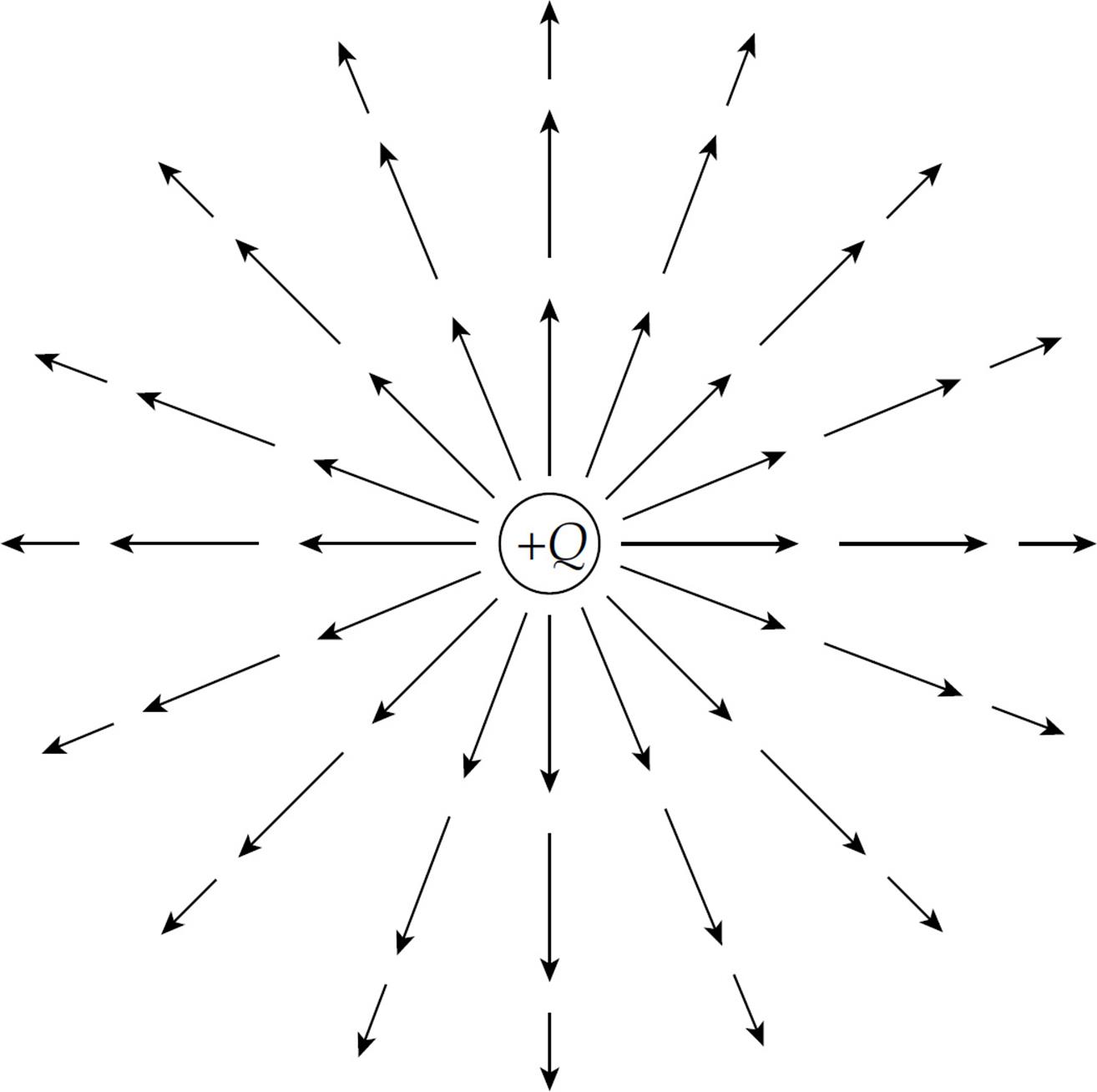
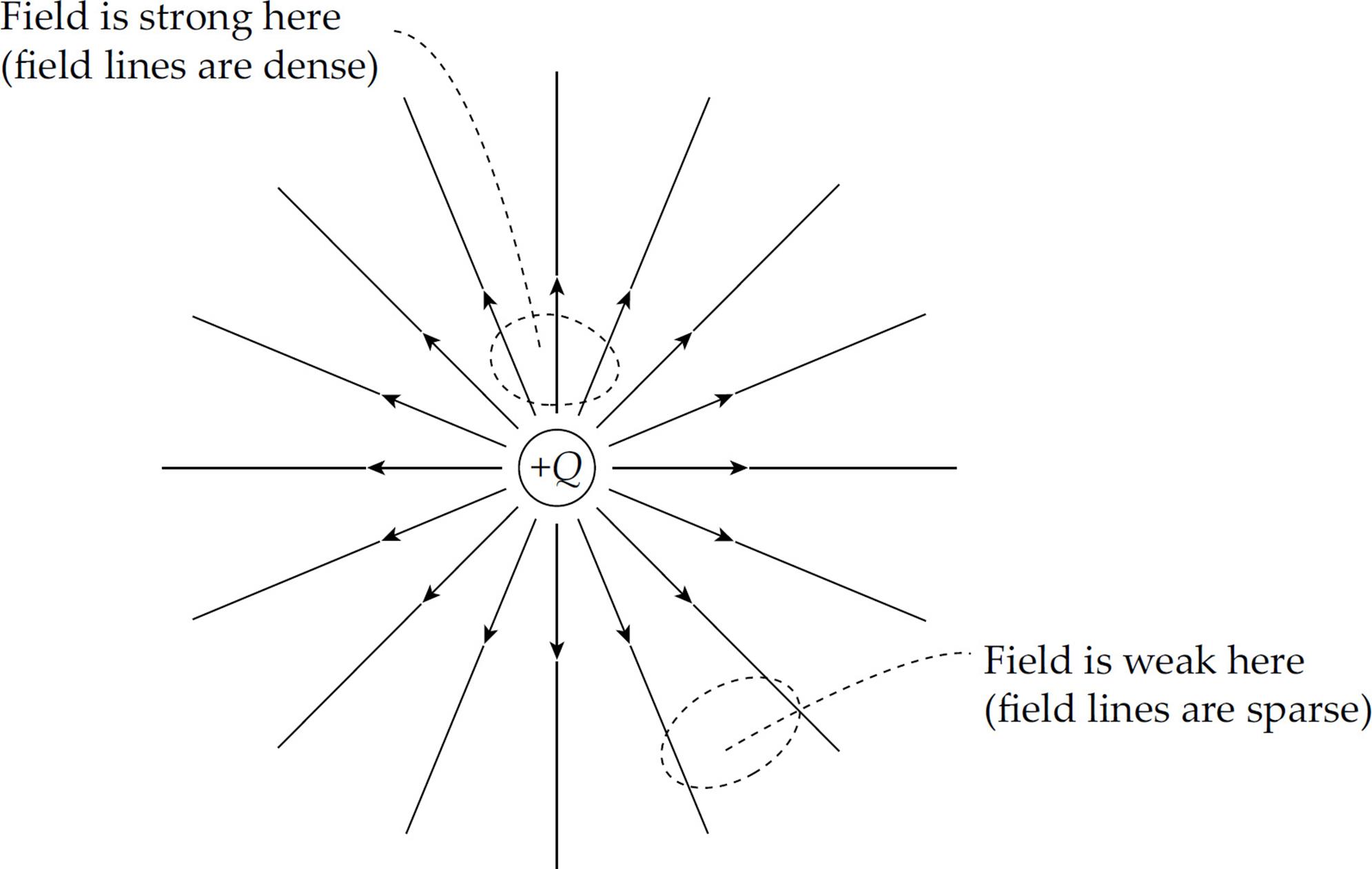
What would the electric field of a positive charge Q look like? Since the test charge used to measure the field is positive, every electric field vector would point radially away from the source charge. If the source charge is positive, the electric field vectors point away from it; if the source charge is negative, then the field vectors point toward it. And, since the force decreases as we get farther away from the charge (as 1/r²), so does the electric field. This is why the electric field vectors farther from the source charge are shorter than those that are closer.

Since the force on the test charge q has a strength of qQ/4πε₀r², when we divide this by q, we get the expression for the strength of the electric field created by a point-charge source of magnitude Q:

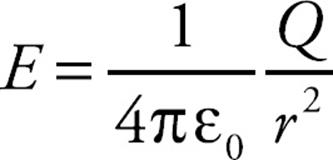
To make it easier to sketch an electric field, lines are drawn through the vectors such that the electric field vector is tangent to the line everywhere it’s drawn.

Now, your first thought might be that obliterating the individual field vectors deprives us of information, since the length of the field vectors told us how strong the field was. Well, although the individual field vectors are gone, the strength of the field can be figured out by looking at the density of the field lines. Where the field lines are denser, the field is stronger.

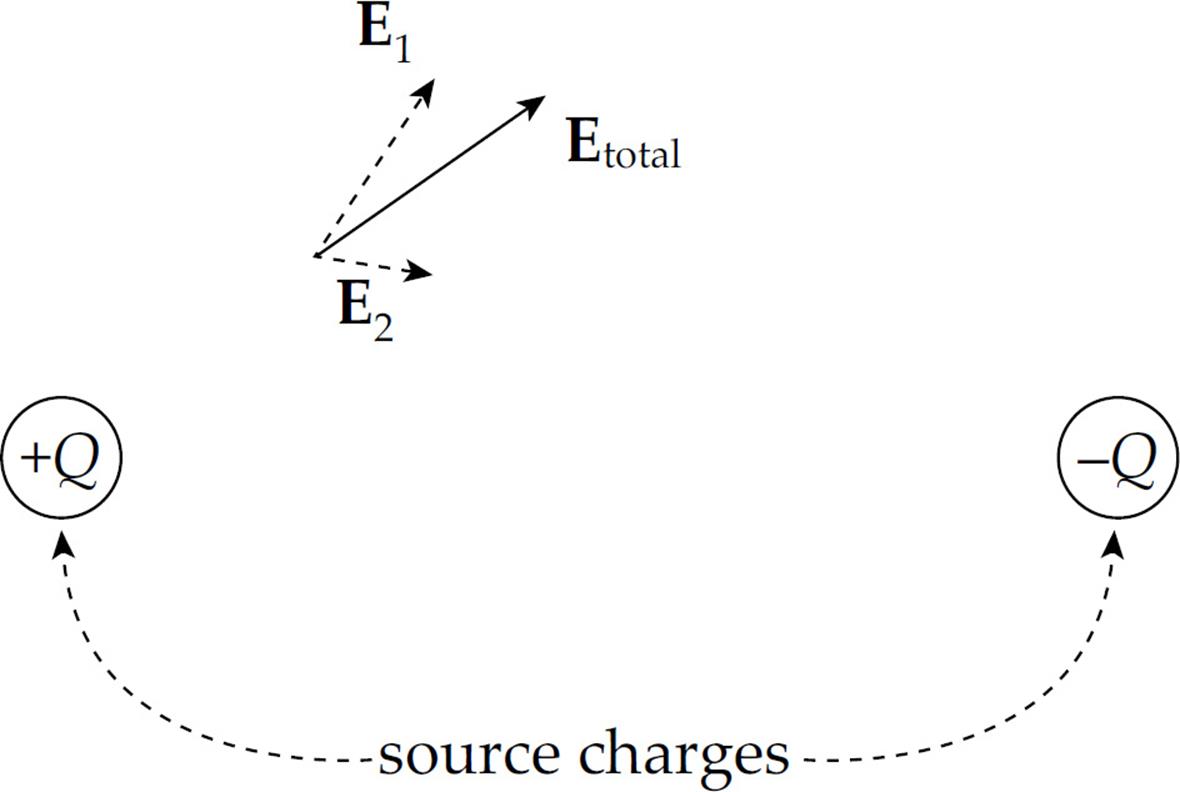
Electric field vectors can be added like any other vectors. If we had two source charges, their fields would overlap and effectively add; a third charge wandering by would feel the effect of the combined field. At each position in space, add the electric field vector due to one of the charges to the electric field vector due to the other charge: E_total = E₁ + E₂. (This is superposition again.) In the diagram below, E₁ is the electric field vector at a particular location due to the charge +Q, and E₂ is the electric field vector at that same location due to the other charge, –Q. Adding these vectors gives the overall field vector E_total at that location.

If this is done at enough locations, the electric field lines can be sketched.

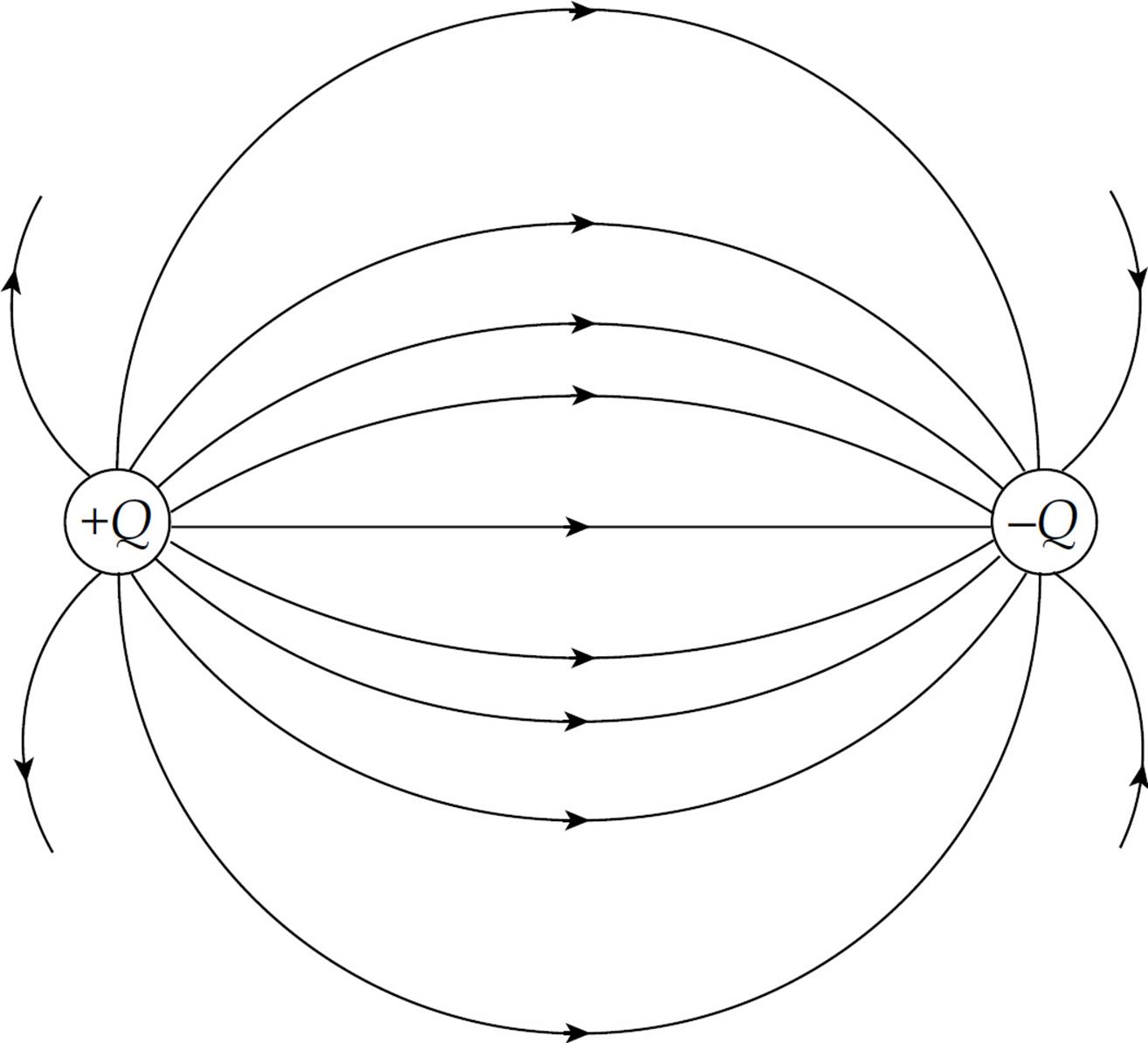
Note that, like electric field vectors, electric field lines always point away from positive source charges and toward negative ones. Two equal but opposite charges, like the ones shown in the diagram above, form a pair called an electric dipole.

If a positive charge +q were placed in the electric field above, it would experience a force that is tangent to, and in the same direction as, the field line passing through +q’s location. After all, electric fields are sketched from the point of view of what a positive test charge would do. On the other hand, if a negative charge –q were placed in the electric field, it would experience a force that is tangent to, but in the direction opposite from, the field line passing through –q’s location.

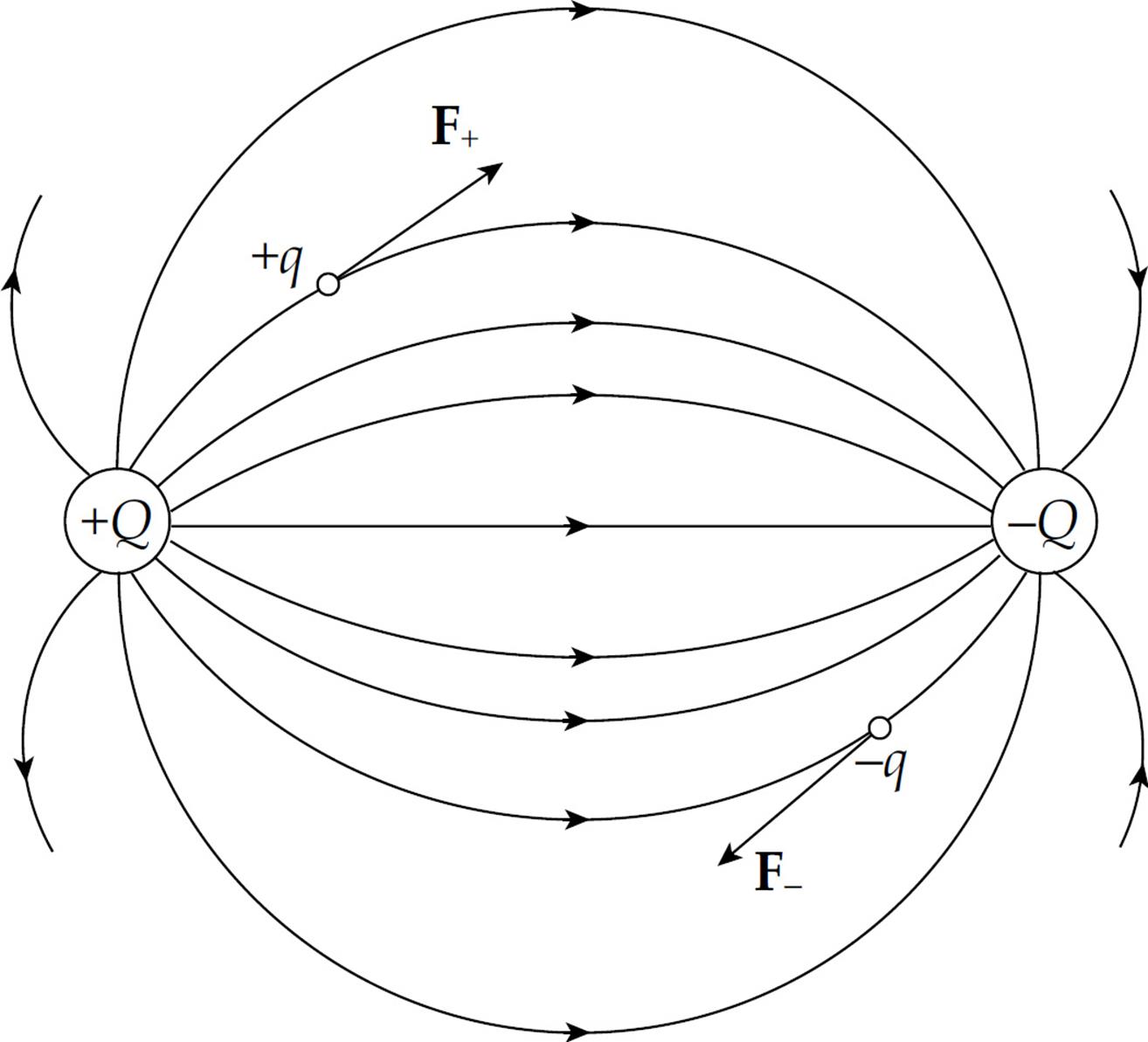
Finally, notice that electric field lines never cross.

Example 5 A charge q = +3.0 nC is placed at a location at which the electric field strength is 400 N/C. Find the force felt by the charge q.

Solution. From the definition of the electric field, we have the following equation:

F_on _q = qE

Therefore, in this case, F_on _q = qE = (3 × 10^–9 C)(400 N/C) = 1.2 × 10^–6 N.

Example 6 A proton is released from rest in a uniform electric field with a strength of 500 N/C. Find the acceleration of the proton and determine the speed of the proton when it has moved half a meter.

Solution. From the definition of the electric field, we can calculate the force and then use Newton’s Second Law to determine the acceleration.

F_{on q} = qE= ma
(1.6 × 10^–19)(500) = (1.67 × 10^–27)a
a = 4.79 × 10¹⁰ m/s²

We can use the constant acceleration equations to solve for the speed of the proton after traveling 1 m.

v₂² = v₁² + 2ax ⇒ v₂² = 2(4.79 × 10¹⁰)(0.5)
v₂ = 2.19 × 10⁵ m/s

Example 7 A dipole is formed by two point charges, each of magnitude 4.0 nC, separated by a distance of 6.0 cm. What is the strength of the electric field at the point midway between them?

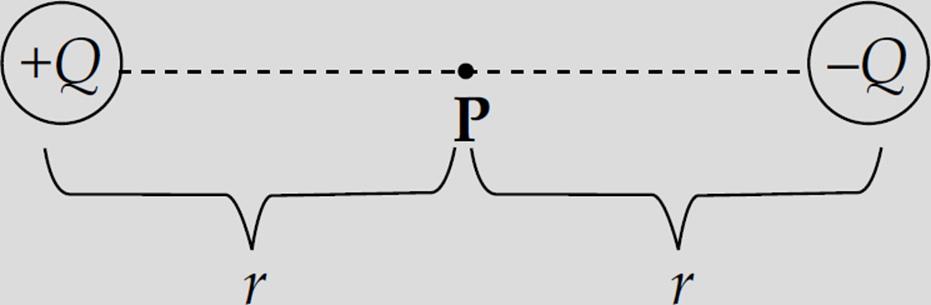
Solution. Let the two source charges be denoted +Q and –Q. At Point P, the electric field vector due to +Q would point directly away from +Q, and the electric field vector due to –Q would point directly toward –Q. Therefore, these two vectors point in the same direction (from +Q to –Q), so their magnitudes would add.

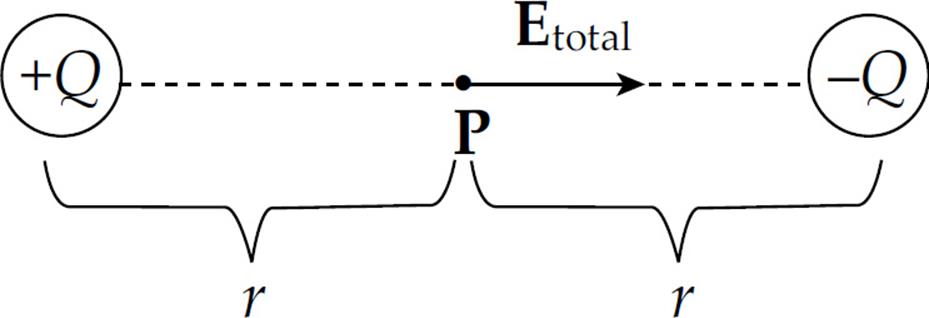
Using the equation for the electric field strength due to a single point charge, we find that

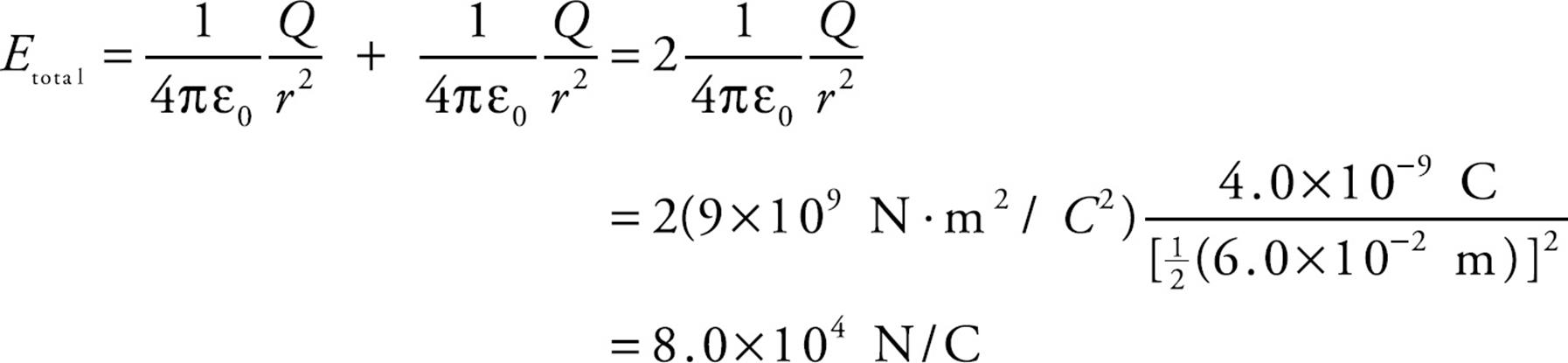
Example 8 If a charge q = –5.0 pC were placed at the midway point described in the previous example, describe the force it would feel. (“p” is the abbreviation for “pico-,” which means 10^–12.)

Solution. Since the field E at this location is known, the force felt by q is easy to calculate:

F_on _q = qE = (–5.0 × 10^–12 C)(8.0 × 10⁴ N/C to the right) = 4.0 × 10^–7 N to the left

Example 9 What can you say about the electric force that a charge would feel if it were placed at a location at which the electric field was zero?

Solution. Remember that F_on _q = qE. So if E = 0, then F_on _q = 0. Zero field means zero force.

Example 10 Positive charge is distributed uniformly over a large, horizontal plate, which then acts as the source of a vertical electric field. An object of mass 5 g is placed at a distance of 2 cm above the plate. If the strength of the electric field at this location is 10⁶ N/C, how much charge would the object need to have in order for the electrical repulsion to balance the gravitational pull?

Solution. Clearly, since the plate is positively charged, the object would also have to carry a positive charge so that the electric force would be repulsive.

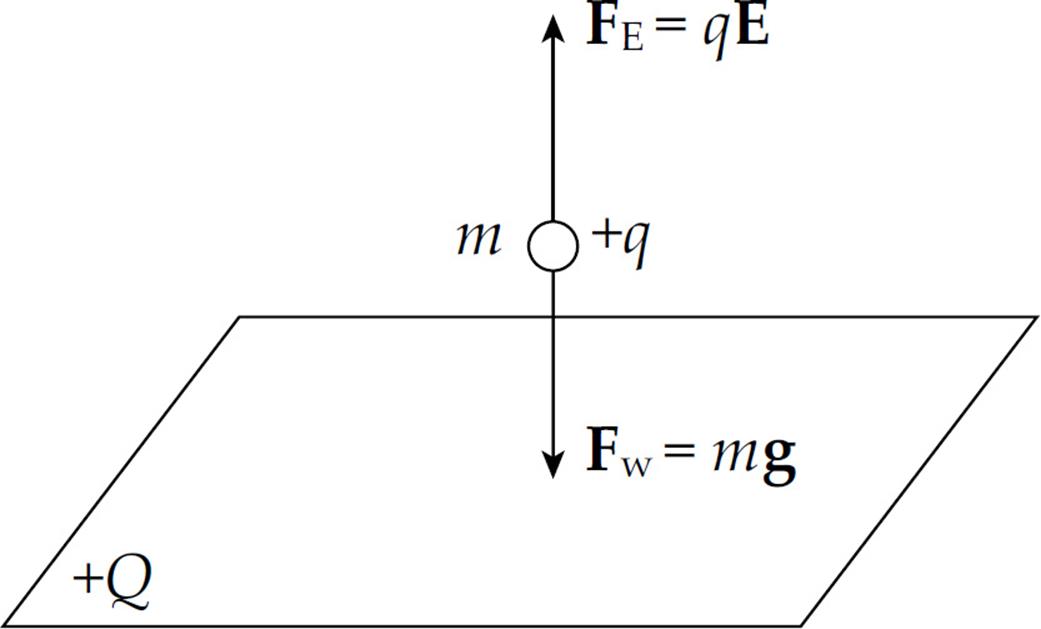
Let q be the charge on the object. Then, in order for F_E to balance mg, we must have

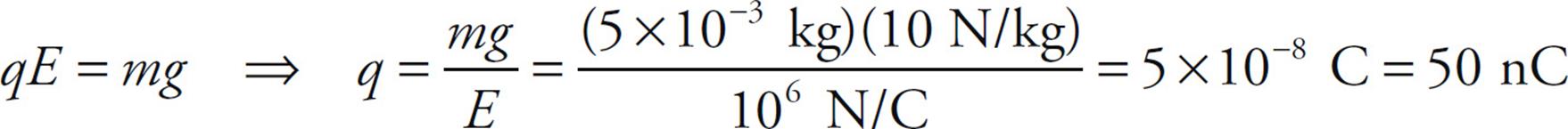
Example 11 A thin, nonconducting rod that carries a uniform linear charge density λ is bent into a semicircle of radius R. Find the electric field at the center of curvature of the semicircle.

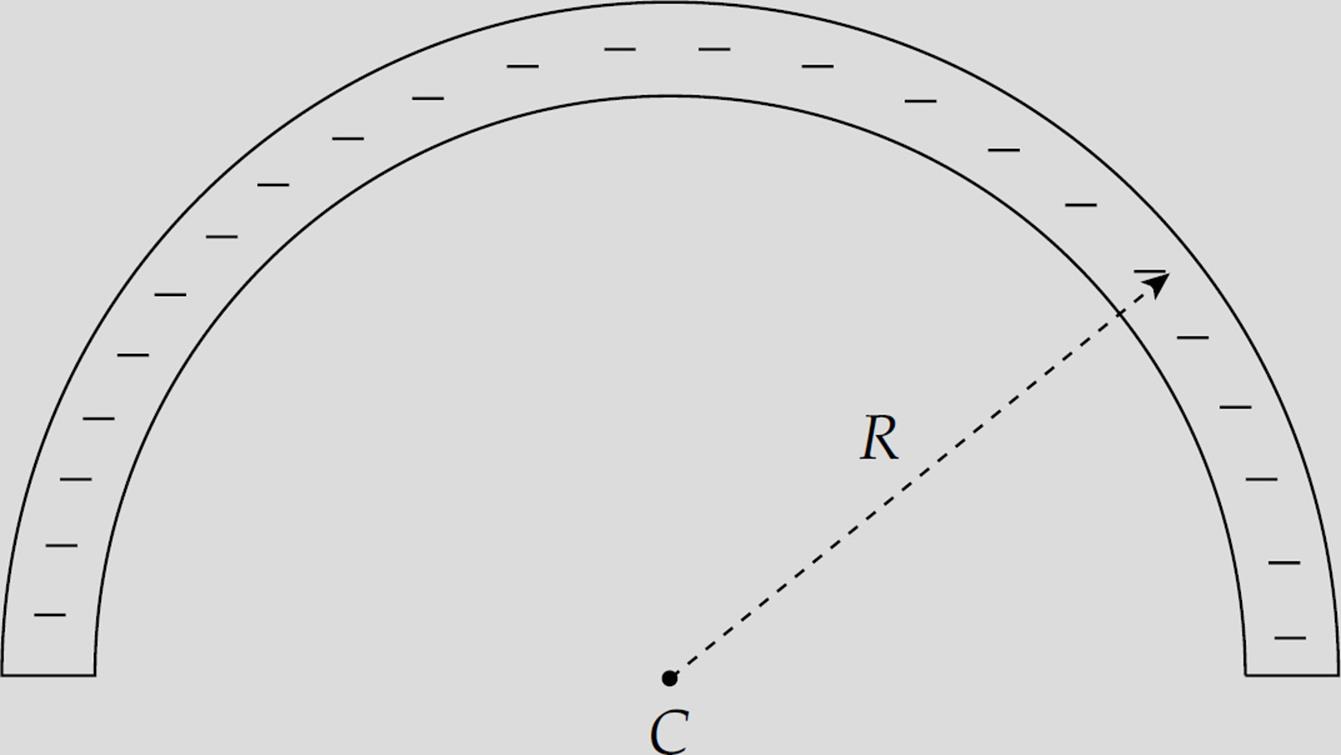
Solution. Refer to the figure below. Consider a small section of the rod subtended by an angle dθ. The length of this section is (by the definition of radian measure) R dθ, so the charge it carries is equal to λ R dθ. The field it creates at C is (1/4πε₀)(λR dθ/R²), pointing directly toward this section.

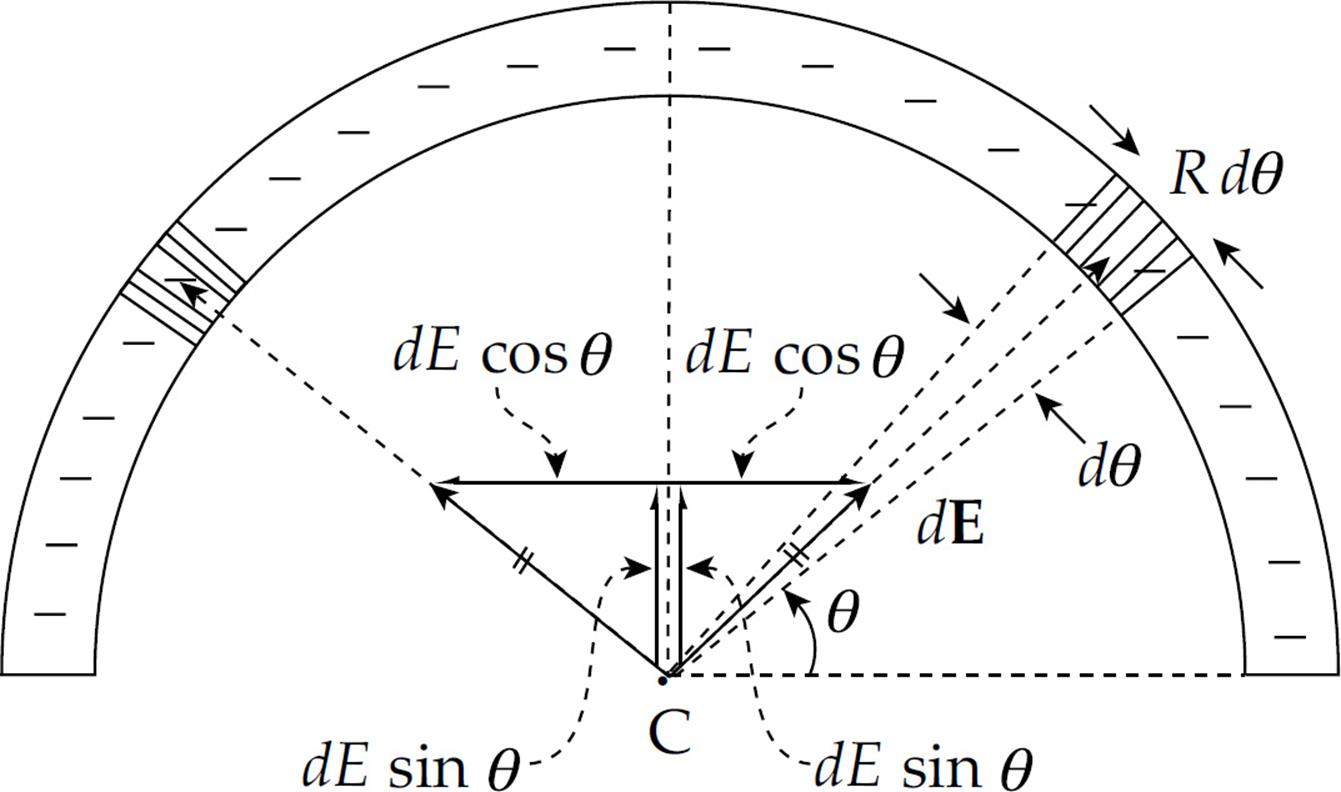
However, another section of the rod creates a field of the same strength and, as the figure shows, cancels out the horizontal component of the field created by the first section. Only the two vertical components, dE sin θ, remain. The total electric field at C, due to all sections of the rod, is found by adding up the individual contributions:

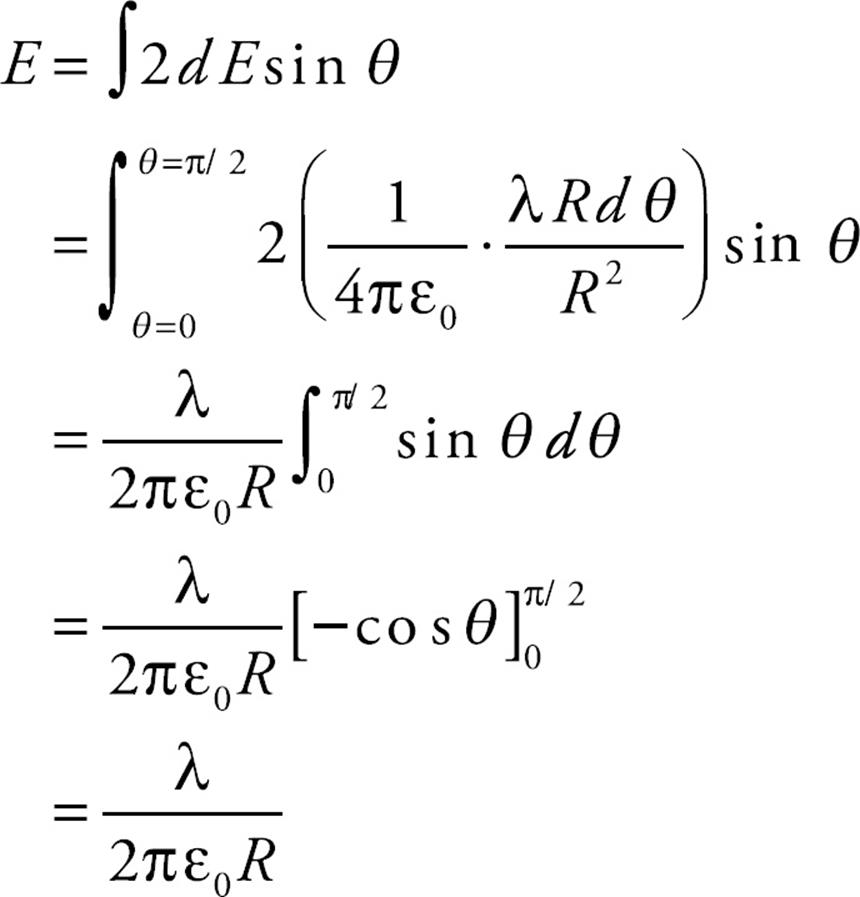
Since the rod is negatively charged, the field E, at C, points upward, toward the rod.

CONDUCTORS AND INSULATORS

Materials can be classified into broad categories based on their ability to permit the flow of charge. If electrons were placed on a metal sphere, they would quickly spread out and cover the outside of the sphere uniformly. These electrons would be free to flow through the metal and redistribute themselves, moving to get as far away from each other as they could. Materials that permit the flow of excess charge are called conductors; they conduct electricity. Metals are the best examples of conductors, but other conductors are aqueous solutions that contain dissolved electrolytes (such as salt water). Metals conduct electricity because the structure of a typical metal consists of a lattice of nuclei and inner-shell electrons, with about one electron per atom not bound to its nucleus. Electrons are free to move about the lattice, creating a sort of sea of mobile (or conduction) electrons. This freedom allows excess charge to flow freely.

Insulators, on the other hand, closely guard their electrons—and even extra ones that might be added. Electrons are not free to roam throughout the atomic lattice. Examples of insulators are glass, wood, rubber, and plastic. If excess charge is placed on an insulator, it stays put.

Midway between conductors and insulators is a class of materials known as semiconductors. As the name indicates, they’re more or less conductors. That is, they are less conducting than most metals, but more conducting than most insulators. Examples of semiconducting materials are silicon and germanium.

An extreme example of a conductor is the superconductor. This is a material that offers absolutely no resistance to the flow of charge; it is a perfect conductor of electric charge. Many metals and ceramics become superconducting when they are brought to extremely low temperatures.

Example 12 A solid sphere of copper is given a negative charge. Discuss the electric field inside and outside the sphere.

Solution. The excess electrons that are deposited on the sphere move quickly to the outer surface (copper is a great conductor). Any excess charge on a conductor resides entirely on the outer surface.

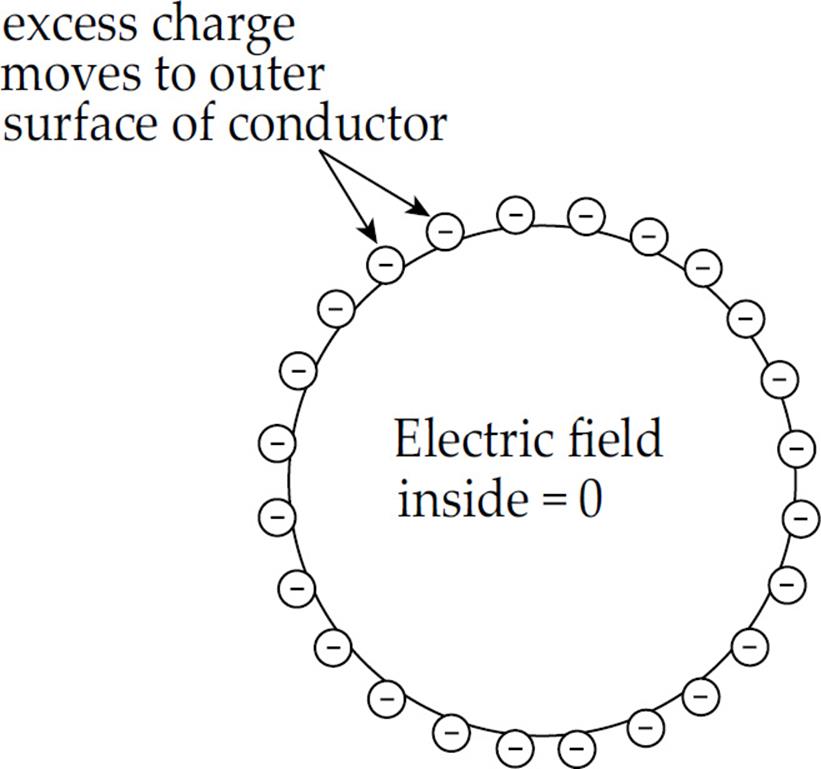
Once these excess electrons establish a uniform distribution on the outer surface of the sphere, there will be no net electric field within the sphere. Why not? Since there is no additional excess charge inside the conductor, there are no excess charges to serve as a source or sink of an electric field line cutting down into the sphere, because field lines begin or end on excess charges.

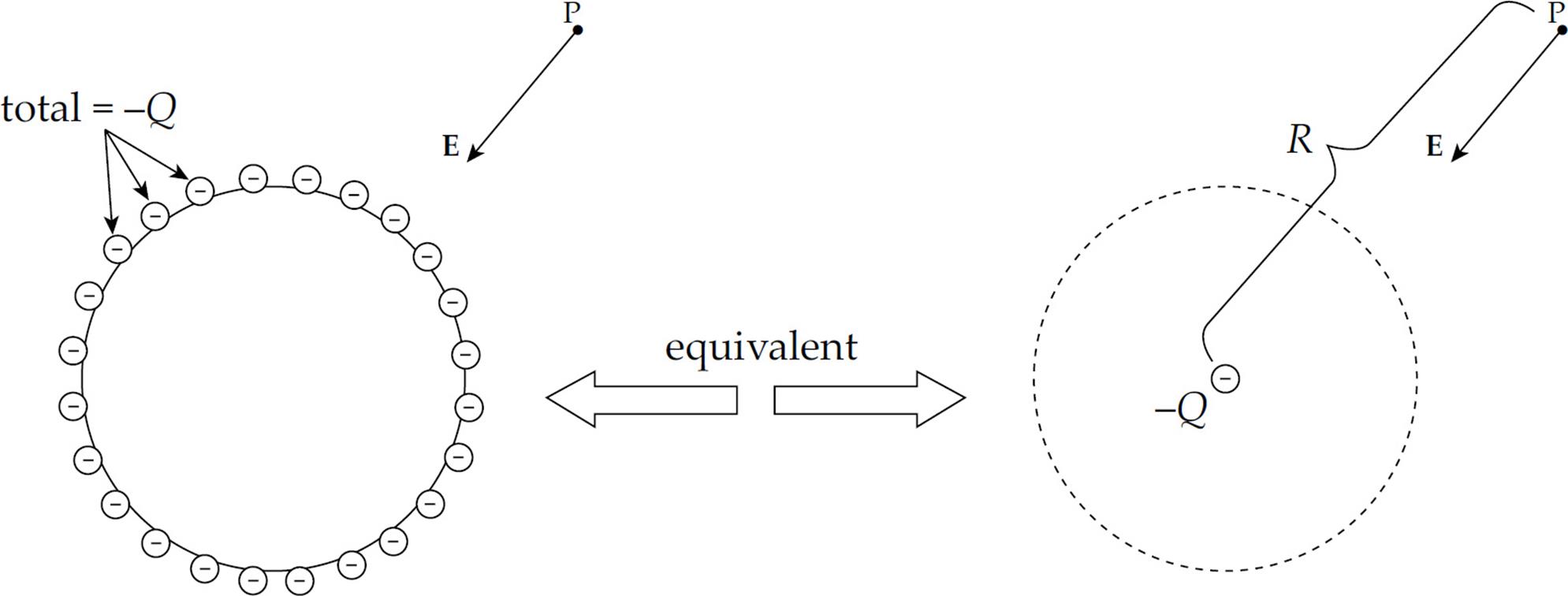
There can be no electrostatic field within the body of a conductor.

In fact, you can shield yourself from electric fields simply by surrounding yourself with metal. Charges may move around on the outer surface of your cage, but within the cage, the electric field will be zero. For points outside the sphere, it can be shown that the sphere behaves as if all its excess charge were concentrated at its center. (Remember that this is just like the gravitational field due to a uniform spherical mass.) Also, the electric field is always perpendicular to the surface, no matter what shape the surface may be. See the diagram below.

GAUSS’S LAW

For individual point charges, we can compute the electric field they produce by using the equation E = Q/4πε₀r² for each source charge, Q, then add up the resulting electric field vectors to obtain the net field. However, if the source charge is spread over a wire or a plate or throughout a cylinder or a sphere, then we need another method for determining the resulting electric field.

First, let’s discuss the concept of flux. Consider the flow of a fluid through a pipe and imagine a small rectangular surface perpendicular to the flow. Multiplying the area of this rectangle (A) by the speed of the flow (v) gives the volume of fluid flowing through the surface per unit time. This is called the fluid-volume flux, symbolized Φ (the uppercase Greek letter phi):

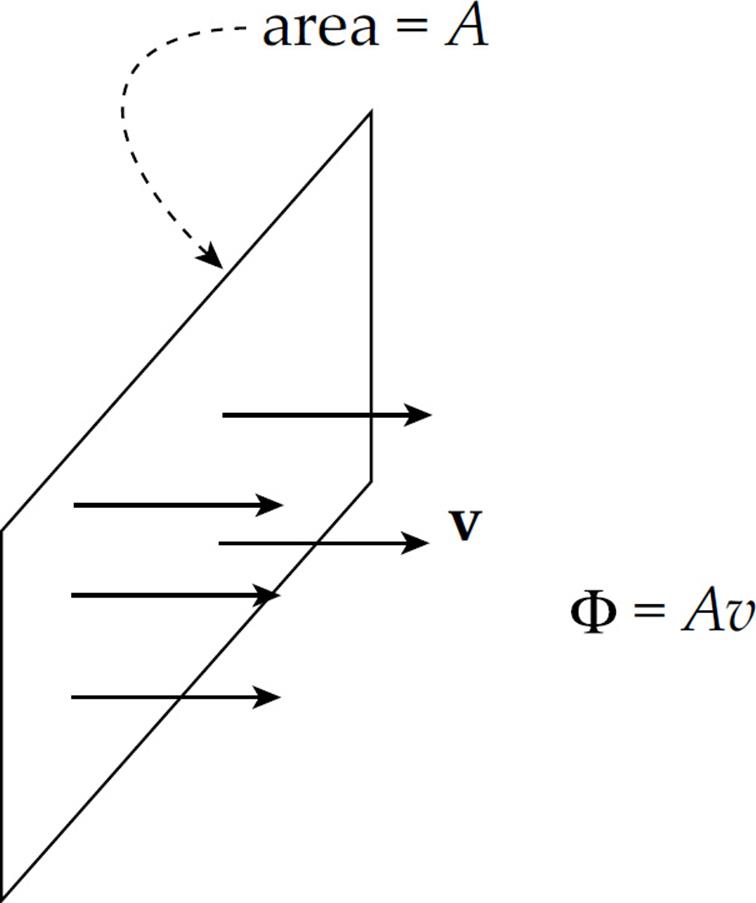
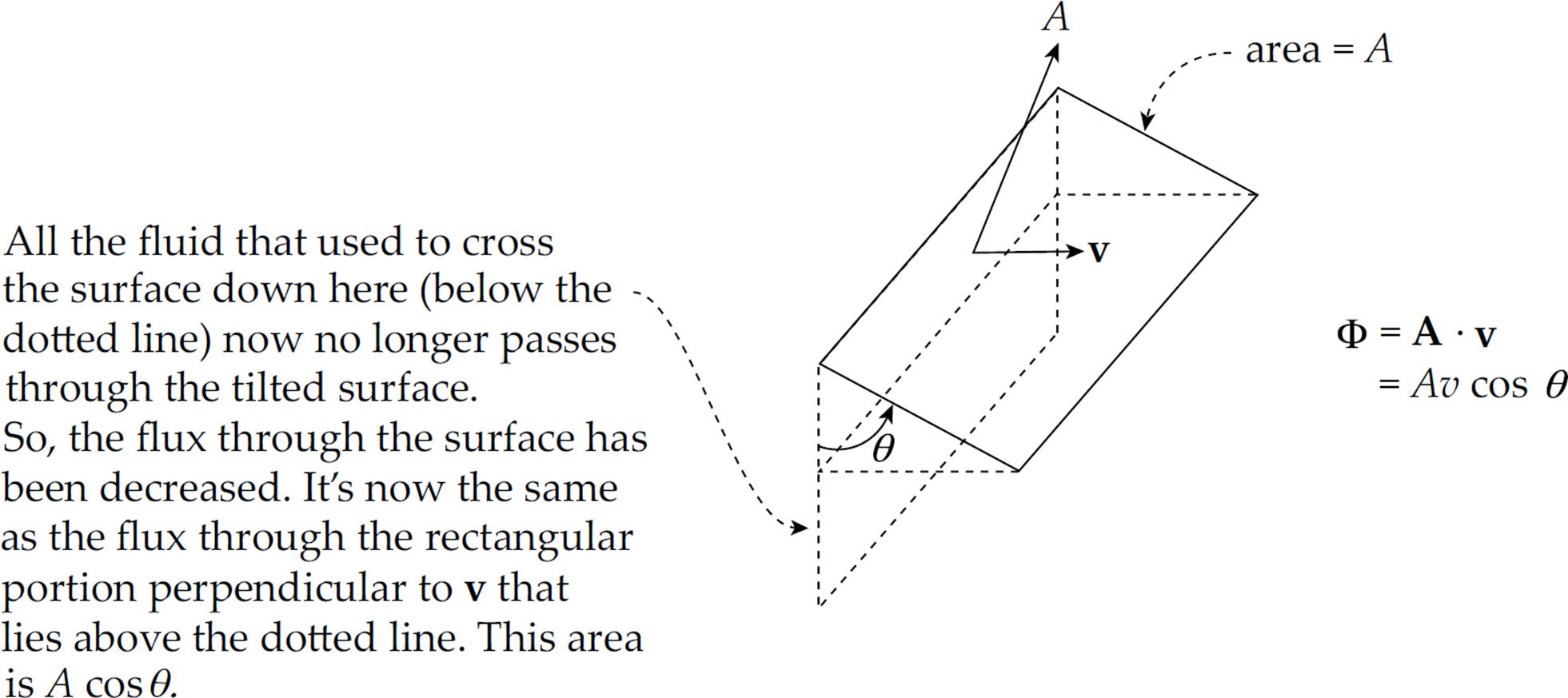
In general, the fluid-volume flux through the surface is given by the equation Φ = Av cos θ, where θ is the angle between the velocity v of the flow and the normal to the surface. If this rectangular surface were tilted at an angle θ to the flow, then less fluid would flow through it per unit time. In fact, if θ were 90°, then no fluid would flow through the surface. (You might also recognize this as the dot product, Φ = A · v, where A is the vector whose magnitude is A and whose direction is normal to the surface.)

Let’s now apply this same idea to an electric field. Consider a source charge +Q and imagine a tiny patch (area = A) of a spherical surface of radius r. The diagram on the next page shows a cross-section of the situation.

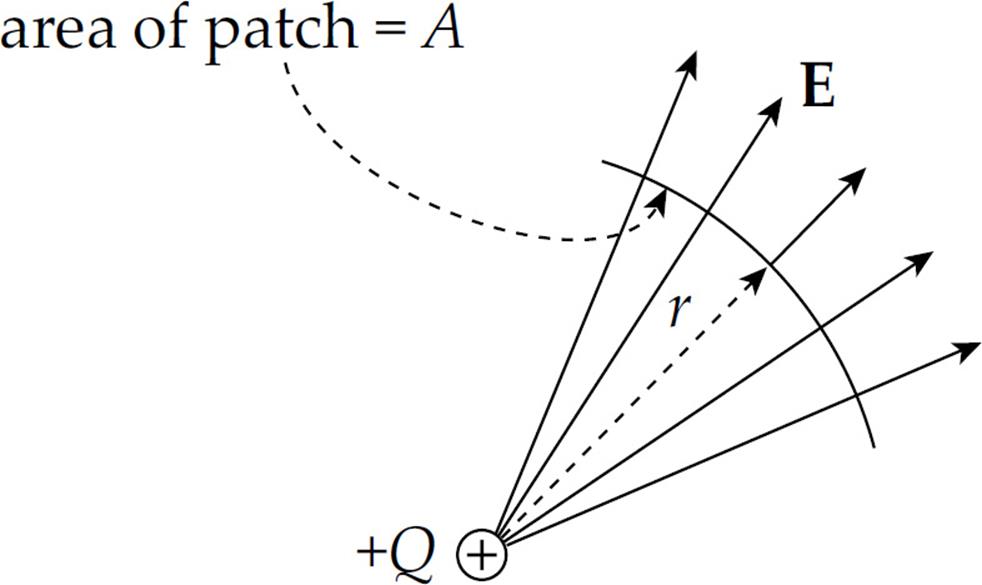
Then we can think of the electric field vectors flowing through the area A and, since E is everywhere perpendicular to this patch area A, the electric flux (Φ_E) would simply be the product: Φ_E = EA. Although the electric field isn’t really flowing like the fluid in the previous discussion, we can still use the same terminology. It might be more appropriate to think of the electric flux as a measure of the amount of electric field passing through the surface.

In general, the electric flux through a patch of area dA is given by the equation:

dΦ_E = E · dA

The total electric flux is then found by adding (that is, integrating) all of the contributions:

Φ_E = d Φ_E = E•dA

Let’s now imagine a closed surface—a sphere, for simplicity—surrounding the charge +Q. Place this closed spherical surface at a distance r from +Q.

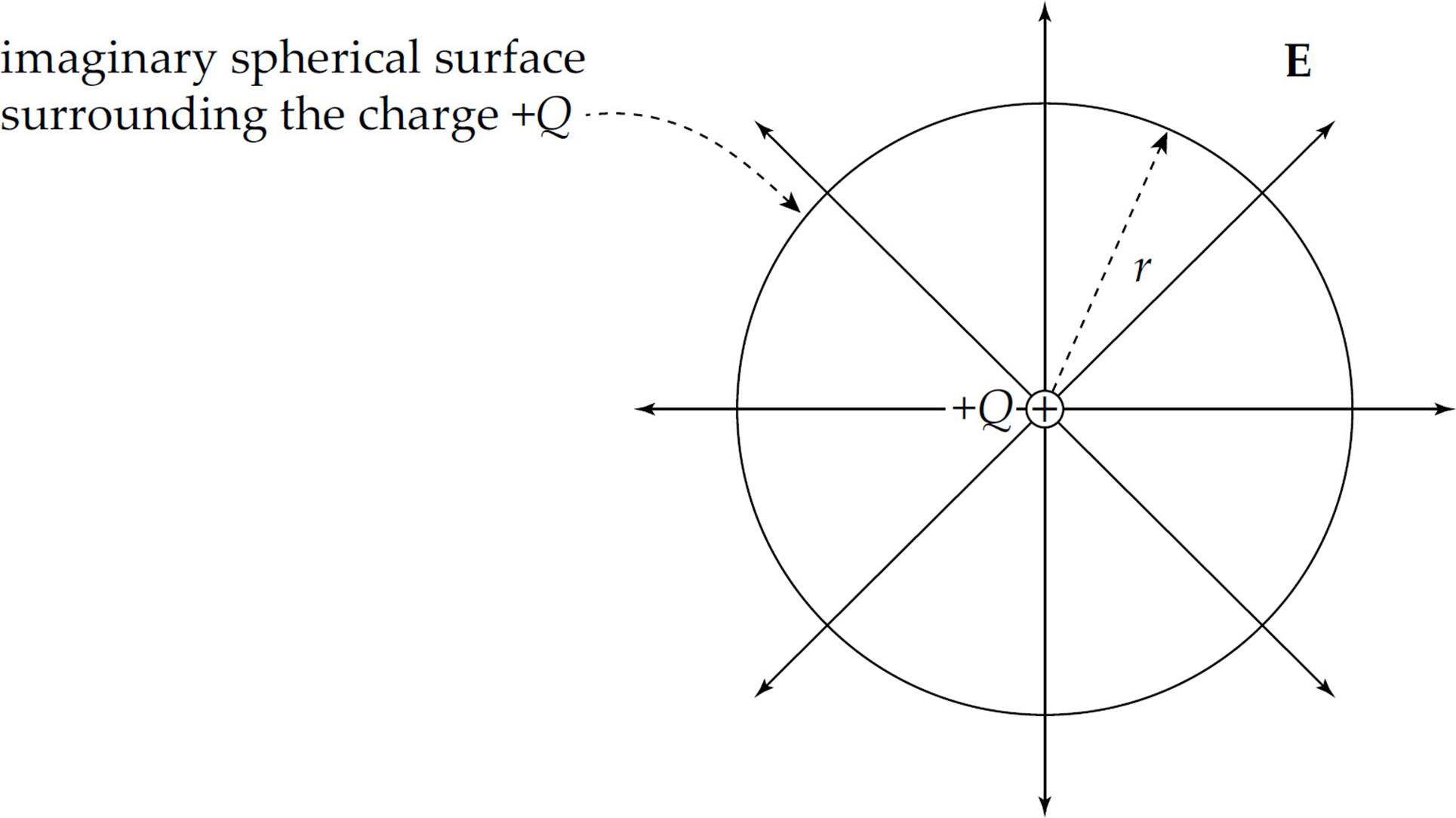
The total flux outward through this closed surface is

Φ_E = EA = E(4πr²), where 4πr² is the surface area of a sphere.

We know what the electric field is at the position of this imaginary sphere; it’s E = Q/4πε₀r². Therefore, the previous equation becomes

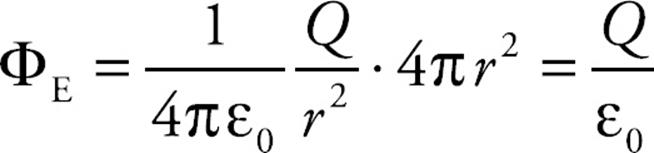
It can be shown that the previous equation holds true for any closed surface; the total electric flux through the surface is equal to 1/ε₀ times the charge enclosed:

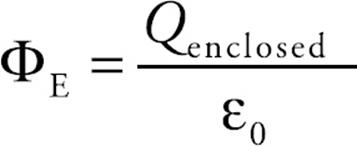
On the equation sheet for the free-response section, this information will be represented as follows:

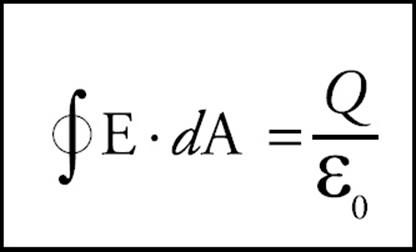
Now you can finally see
why we write Coulomb’s
constant, k₀, as 1/(4πε₀). It
makes the 4π’s cancel out
in this equation.

This is Gauss’s Law. The quantity Q_enclosed is the algebraic sum of the charges inside. For example, if the imaginary closed surface we construct encloses, say, charges of +Q and –3Q, then the total charge enclosed is –2Q, the algebraic sum, so this is Q_enclosed in this case. In fact, many people place a Σ in front of Q_enclosed to remind them that they need to take the sum of the charges enclosed when using Gauss’s Law. The power of Gauss’s Law to determine electric fields is evident if we can write Φ_E in terms of E—and this requires symmetry—because then the equation can be solved for E. The imaginary closed surface that we will construct when using Gauss’s Law to determine an electric field is known as a Gaussian surface.

Example 13 Consider a long, straight wire carrying a total charge of +Q, distributed uniformly along its entire length, L. Use Gauss’s Law to find an expression for the electric field created by the wire.

Solution. By symmetry, the electric field must point radially away from the wire. To take advantage of this symmetry, we will construct a cylindrical Gaussian surface—of length x and radius r—around the wire:

The electric field is always perpendicular to the lateral surface area, A, of the cylinder. Therefore, the electric flux through the cylinder is equal to EA = E(2πrx). The flux through each of the two lids of the cylinder is zero, because E is parallel to the end surfaces (so E • dA = E • dA cos 90° = 0). So the total electric flux through the Gaussian surface is Φ_E = 0 + E(2πrx) + 0 = E(2πrx). Next we need to know the charge enclosed by the Gaussian surface. Since a total charge of Q is distributed uniformly along the entire length L of the wire, the amount of charge on a section of length x is (x/L)Q. Therefore, Gauss’s Law becomes

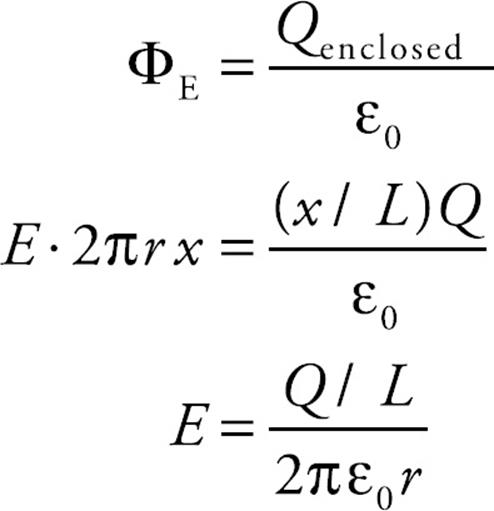
The ratio Q/L (charge per unit length) is called the linear charge density, and is denoted by λ; using this notation, the electric field at a distance r from the wire is given by the equation E = λ/(2πε₀r). (If the charge on the wire were –Q, then the field would point radially inward.)

Example 14 A very large rectangular plate has a surface charge density of + σ (this is the charge per unit area). Use Gauss’s Law to determine an expression for the electric field it creates.

Solution. By symmetry, the electric field lines must be perpendicular to the plate. We will construct a cylindrical Gaussian surface, with cross-sectional area A and total length 2r, perpendicular to the plate:

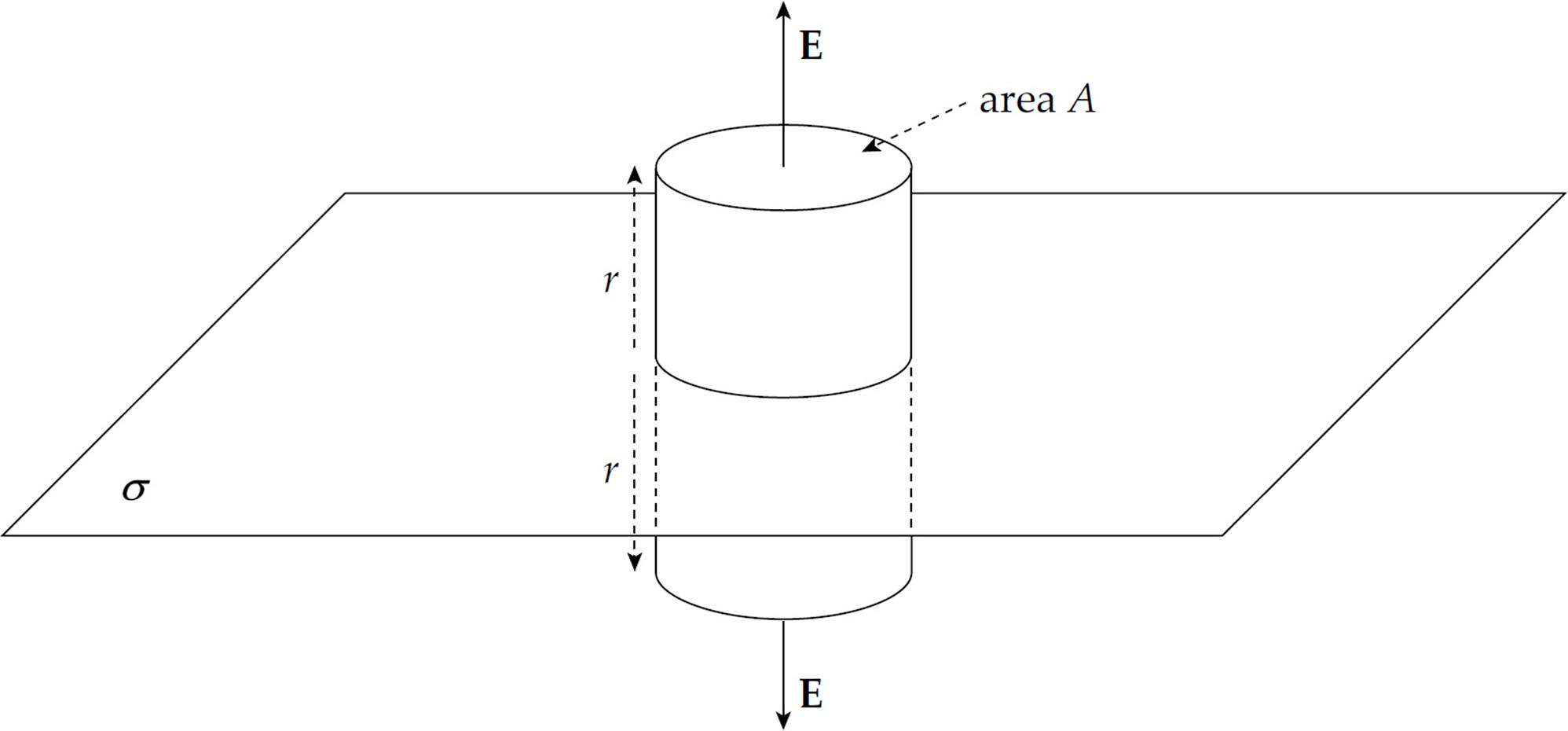
The electric flux through the lateral surface area is now zero, since E is parallel to the cylindrical surface here. However, there is flux through the end caps: EA + EA = 2EA. (Flux outward from the closed surface is counted as positive; flux inward is counted as negative.) Therefore,

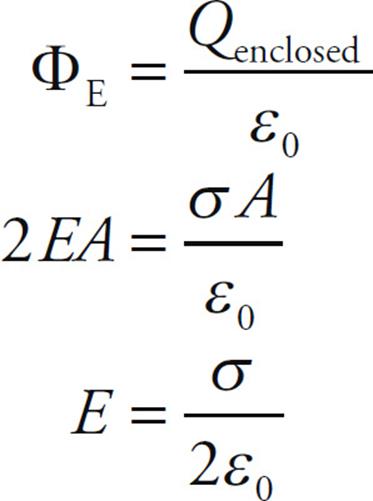
The electric field does not depend on the distance r from the plate. This would only be true if the plate had infinite area. In practical terms, this result means that if we are close to a very large plate (and away from its edges), then the plate looks infinite, and moving a small amount toward or away from the plate won’t make much difference; the electric field will remain essentially constant.

Example 15 A nonconducting sphere of radius a has excess charge distributed throughout its volume so that the volume charge density ρ as a function of r (the distance from the sphere’s center) is given by the equation ρ(r) = ρ₀(r/a)², where ρ₀ is a constant. Determine the electric field at points inside and outside the sphere.

Solution. In order to apply Gauss’s Law, we need to find the total charge enclosed by a Gaussian surface of radius r. Since the charge density depends on r only, consider a thin spherical shell of radius R and thickness dR.

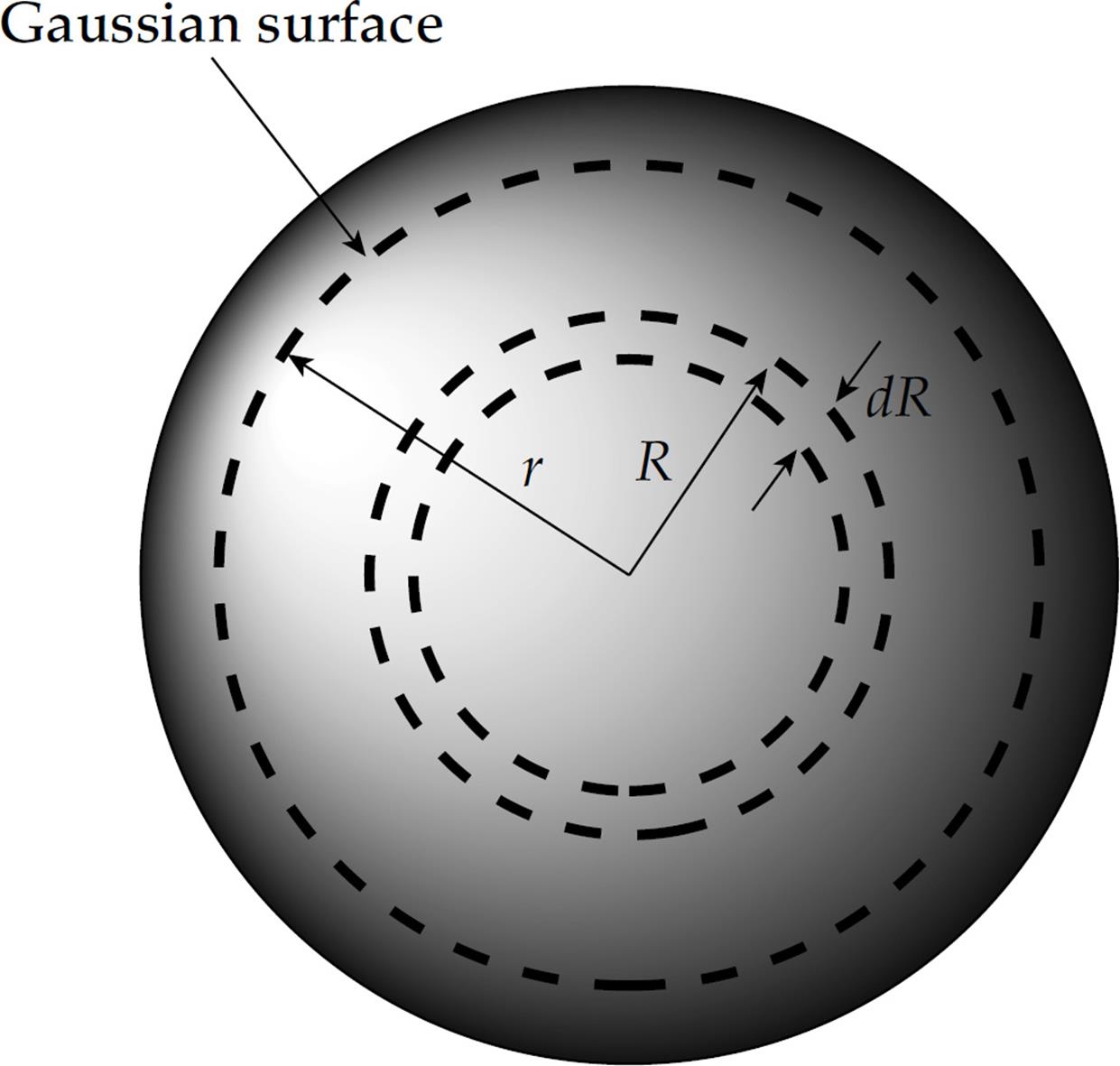
The shell’s volume is dV = 4πR² dR, so the charge contained in the shell is

dQ = ρ dV= ρ₀(R/a)² · 4πR² dR

The total charge enclosed within a sphere of radius r is found by adding up all the charges on these shells, from R = 0 to R = r:

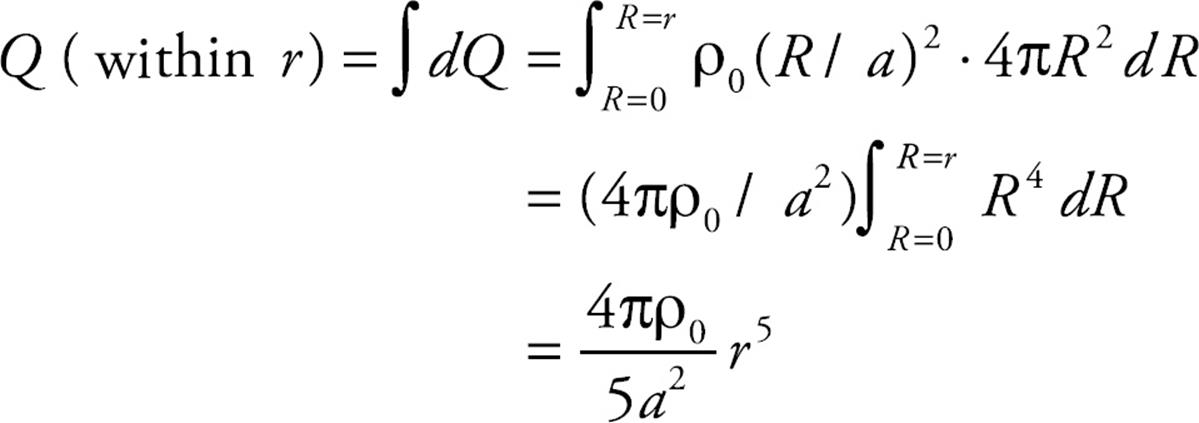
The electric flux through the spherical Gaussian surface of radius r is

Φ_E = E A = E(4πr²)

so, by Gauss’s Law,

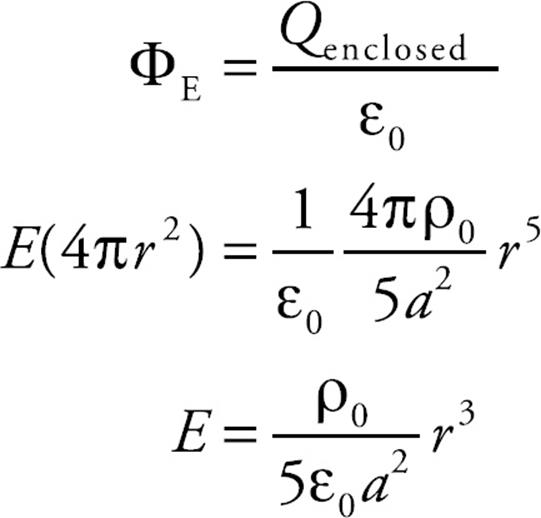
This gives the electric field at all points within the given sphere. For points outside, we first figure out the charge on the entire sphere, which from the integral (*) above with r = a is

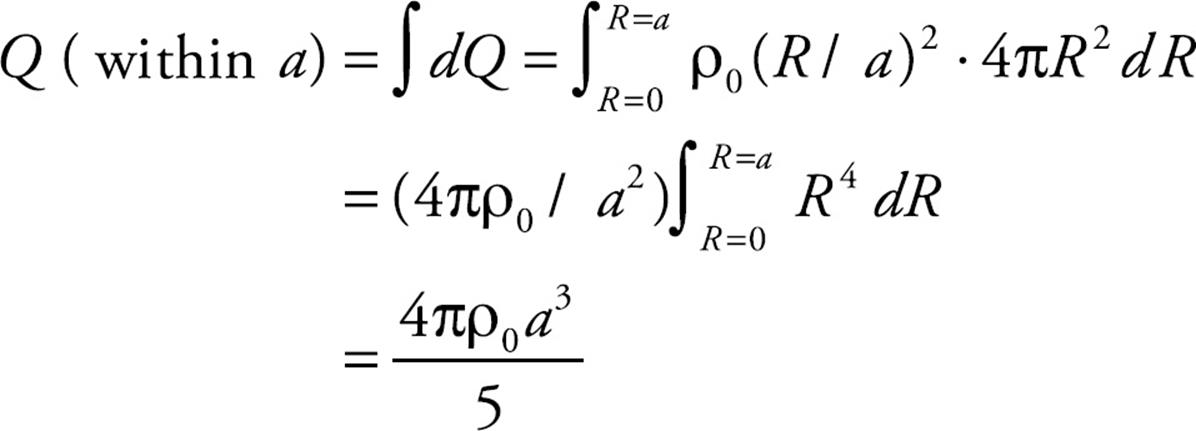
Then, applying Gauss’s Law again on a spherical Gaussian surface of radius r > a, we get

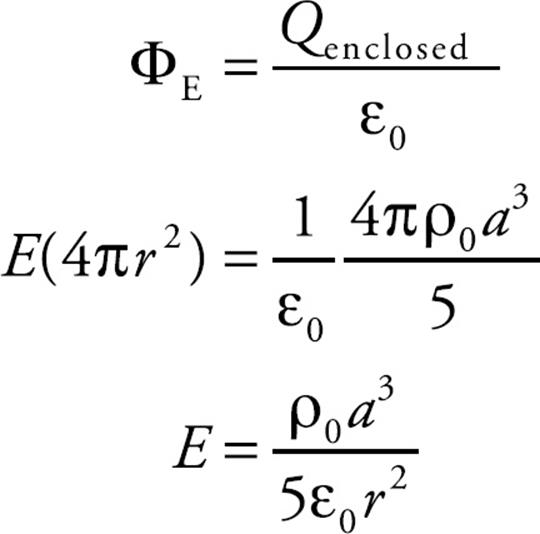
To summarize then we have found

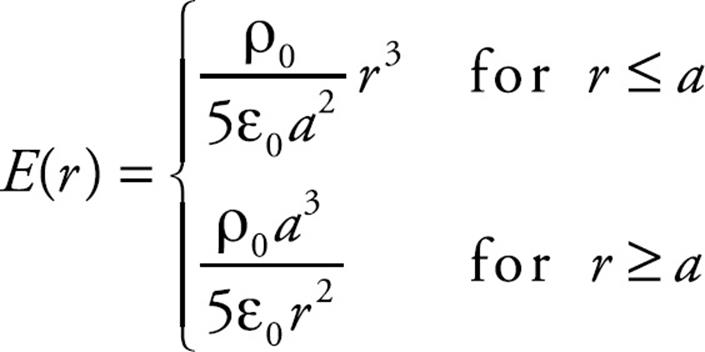
Example 16 Use Gauss’s Law to show that the electric field inside a charged hollow metal sphere is zero.

Solution. Recall that for a conductor, any excess charge resides on its surface. Therefore, if a Gaussian surface is constructed anywhere within the metal, it contains no net charge, so E = 0 everywhere inside the sphere.

Example 17 Consider a neutral, hollow metal sphere. Imagine that a charge of +q could be introduced into the cavity, insulated from the inner wall. What will happen?

Solution. A static electric field cannot be sustained within the body of a conductor. Therefore, enough electrons will migrate to the inner wall of the cavity to form a shield of charge –q around the inside charge +q.

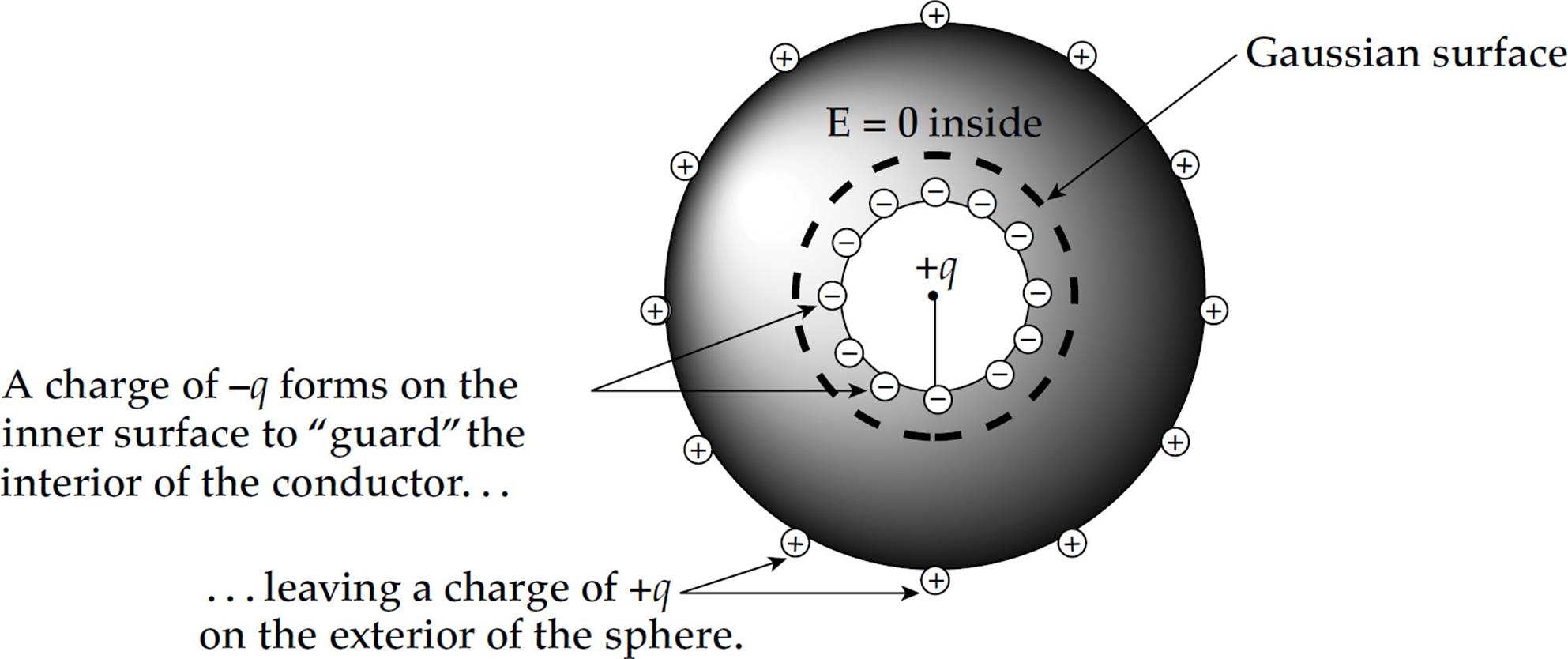
To see why this must be so, if any Gaussian surface surrounding the cavity is drawn within the conductor, then, because E must be 0 inside, the electric flux must be 0, so Q_enclosed must be 0. The only way to ensure that Q_enclosed = 0 is to have a charge of –q on the inner wall of the cavity. Since the sphere was originally neutral, an excess charge of +q will then appear on the outer surface.

Example 18 A solid metal sphere of radius a, carrying a charge of + q, is placed inside and concentric with a neutral hollow metal sphere of inner radius b and outer radius c. Determine the electric field for r < a, a < r < b, b < r < c, and r > c. Also, describe the charge distributions.

Solution. For r < a, the electric field is 0, since there can be no electric field within the body of a conductor. For r between a and b, the inner sphere acts like a point charge of +q at its center, so E = q/(4πε₀r²). For r between b and c, the electric field is again zero, since there can be no electric field within the body of a conductor. For r > c, the ensemble behaves as if all its charge were concentrated at its center, so once again, E = q/(4πε₀r²).

The charge on the sphere of radius a will be at its surface. To protect the interior of the outer spherical shell from an electric field, a charge of –q will reside on the surface of radius b (shielding the charge of +q that’s introduced into the cavity), leaving +q to appear on the outer surface (radius c).

CHAPTER 11 REVIEW QUESTIONS

The answers and explanations can be found in Chapter 16.

Section I: Multiple Choice

1. If the distance between two positive point charges is tripled, then the strength of the electrostatic repulsion between them will decrease by a factor of

(A) 3

(B) 6

(D) 9

(E) 12

2. Two 1 kg spheres each carry a charge of magnitude 1 C. How does F_E, the strength of the electric force between the spheres, compare to F_G, the strength of their gravitational attraction?

(A) F_E < F_G

(B) F_E = F_G

(D) If the charges on the spheres are of the same sign, then F_E > F_G; but if the charges on the spheres are of opposite sign, then F_E < F_G.

(E) Cannot be determined without knowing the distance between the spheres

3. The figure below shows three point charges, all positive. If the net electric force on the center charge is zero, what is the value of y/x?

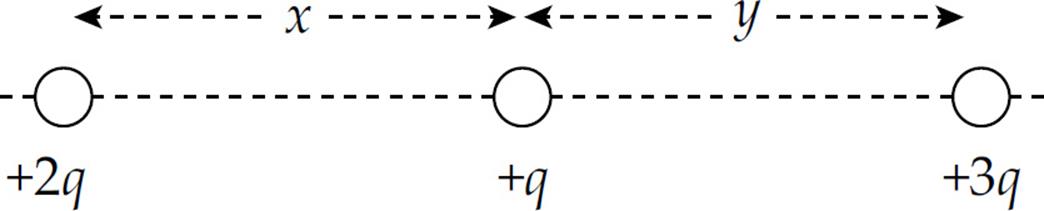
(A) 4/9

(B)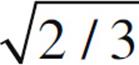

(C)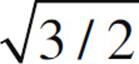

(D) 3/2

(E) 9/4

4. The figure above shows two point charges, +Q and –Q. If the negative charge were absent, the electric field at Point P due to +Q would have strength E. With –Q in place, what is the strength of the total electric field at P, which lies at the midpoint of the line segment joining the charges?

(A) 0

(B) E/4

(D) E

(E) 2E

5. A sphere of charge +Q is fixed in position. A smaller sphere of charge +q is placed near the larger sphere and released from rest. The small sphere will move away from the large sphere with

(A) decreasing velocity and decreasing acceleration

(B) decreasing velocity and increasing acceleration

(D) increasing velocity and decreasing acceleration

(E) increasing velocity and increasing acceleration

6. An object of charge +q feels an electric force F_E when placed at a particular location in an electric field, E. Therefore, if an object of charge –2q were placed at the same location where the first charge was, it would feel an electric force of

(A) –F_E/2

(B) –2F_E

(D) –2F_E/q

(E) –F_E/(2q)

7. A charge of –3Q is transferred to a solid metal sphere of radius r. Where will this excess charge reside?

(A) –Q at the center, and –2Q on the outer surface

(B) –2Q at the center, and –Q on the outer surface

(D) –3Q on the outer surface

(E) –Q at the center, –Q in a ring of radius r, and –Q on the outer surface

8. The figure below shows four point charges and the cross section of a Gaussian surface:

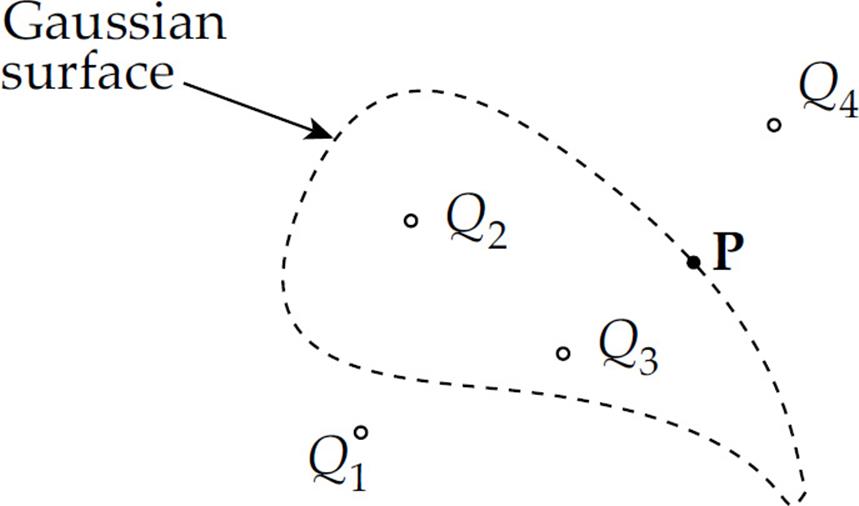
Which of the following statements is true concerning the situation depicted?

(A) The net electric flux through the Gaussian surface depends on all four charges shown, but the electric field at point P depends only on charges Q₂ and Q₃.

(B) The net electric flux through the Gaussian surface depends only on charges Q₂ and Q₃, but the electric field at point P depends on all four charges.

(C) The net electric flux through the Gaussian surface depends only on charges Q₂ and Q₃, and the electric field at point P depends only on charges Q₂, Q₃, and Q₄.

(D) The net electric flux through the Gaussian surface depends only on charges Q₁ and Q₄, and the electric field at point P depends only on charges Q₂ and Q₃.

(E) Both the net electric flux through the Gaussian surface and the electric field at point P depend on all four charges.

9. A nonconducting sphere of radius R contains a total charge of –Q distributed uniformly throughout its volume (that is, the volume charge density, ρ is constant).

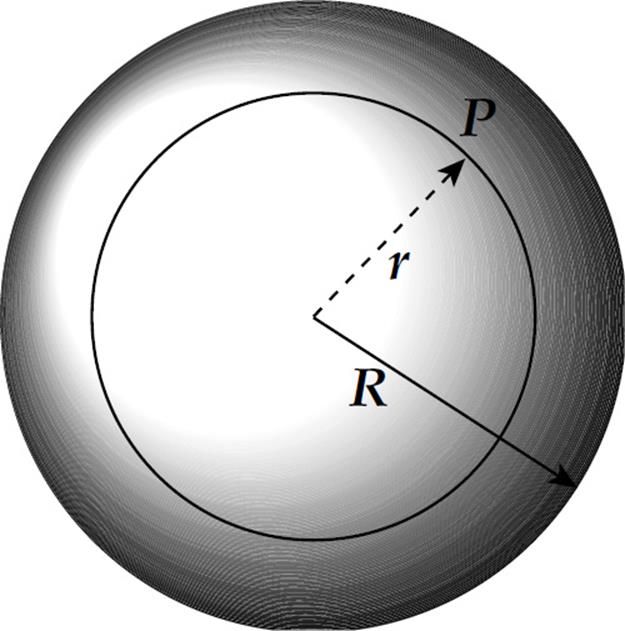
The magnitude of the electric field at Point P, at a distance r < R from the sphere’s center, is equal to

(A)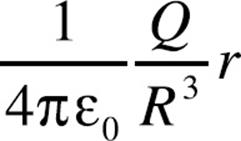

(B)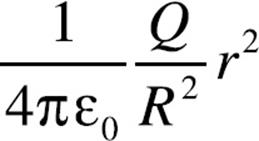

(C)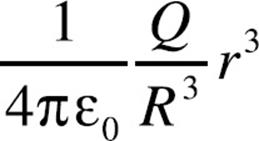

(D)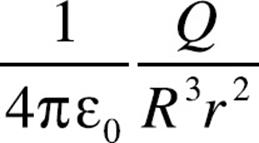

(E)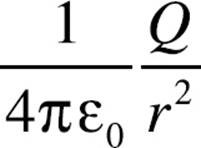

10. Calculate the electric flux through a Gaussian surface of area A enclosing an electric dipole where each charge has magnitude q.

(A) 0

(B) Aq/(4πε₀)

(D) Aq/(4πε₀r)

(E) Aq/(4πε₀r²)

SECTION II: FREE RESPONSE

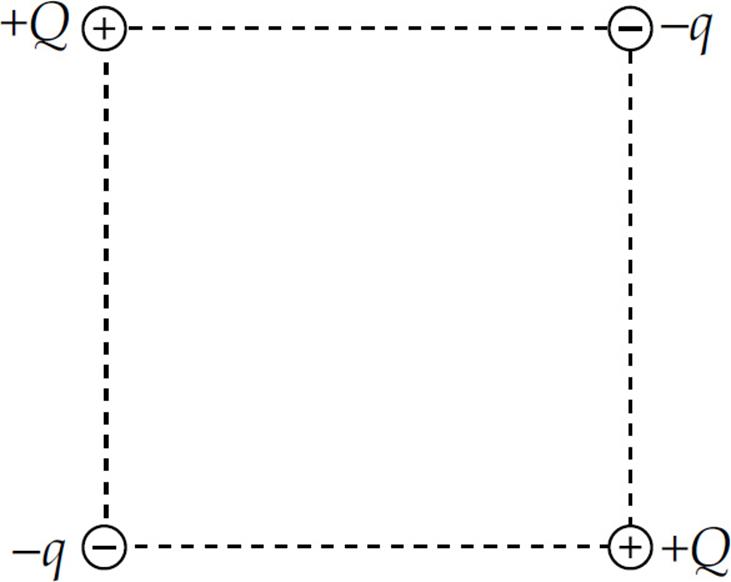
1. In the figure shown, all four charges (+Q, +Q, –q, and –q) are situated at the corners of a square. The net electric force on each charge +Q is zero.

(a) Express the magnitude of q in terms of Q.

(b) Is the net electric force on each charge –q also equal to zero? Justify your answer.

2. Two charges, +Q and +2Q, are fixed in place along the y-axis of an x-y coordinate system as shown in the figure below. Charge 1 is at the point (0, a), and Charge 2 is at the point (0, –2a).

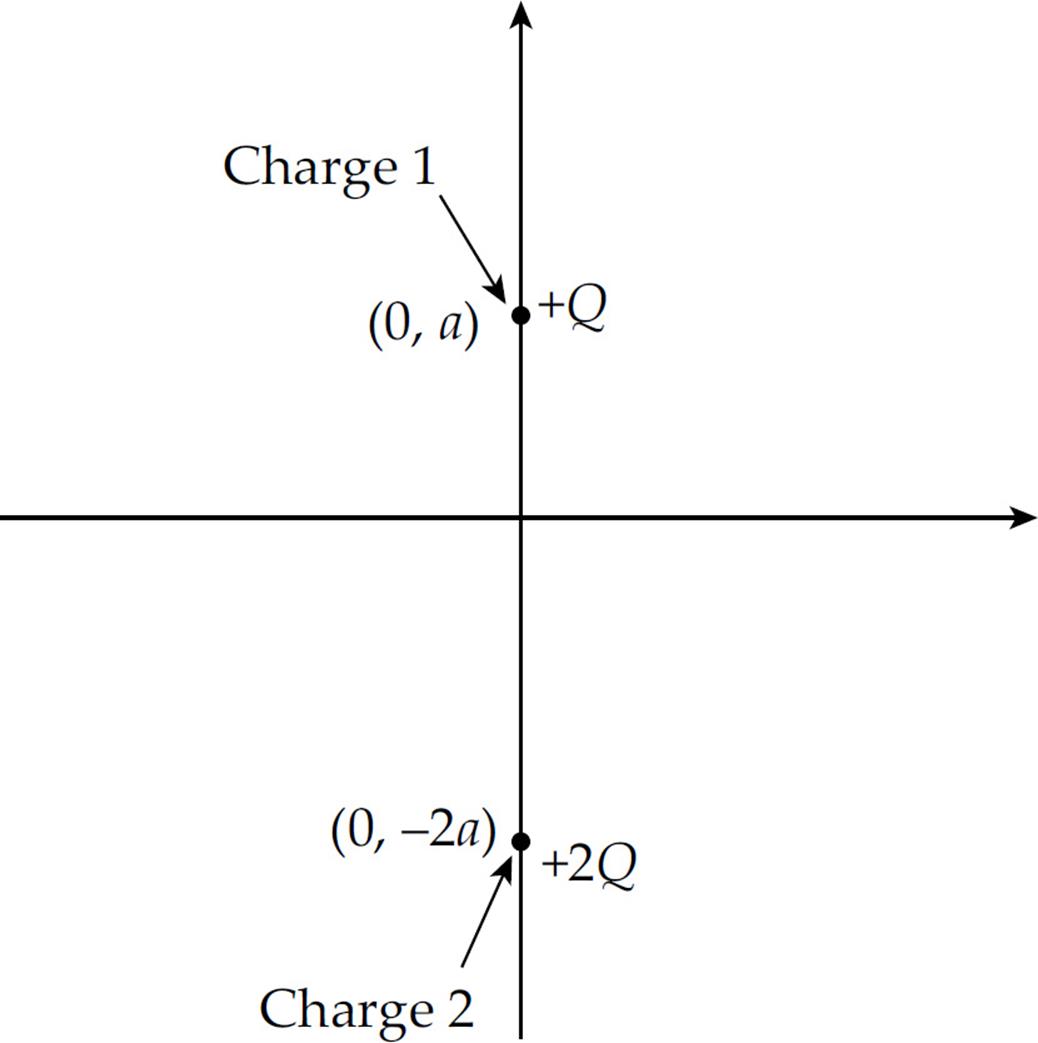
(a) Find the electric force (magnitude and direction) felt by Charge 1 due to Charge 2.

(b) Find the electric field (magnitude and direction) at the origin created by both Charges 1 and 2.

(d) Is there a point on the y-axis where the total electric field is zero? If so, where? If not, explain briefly.

(e) If a small negative charge, –q, of mass m were placed at the origin, determine its initial acceleration (magnitude and direction).

3. A conducting spherical shell of inner radius a and outer radius b is inside (and concentric with) a larger conducting spherical shell of inner radius c and outer radius d. The inner shell carries a net charge of +2q, and the outer shell has a net charge of +3q.

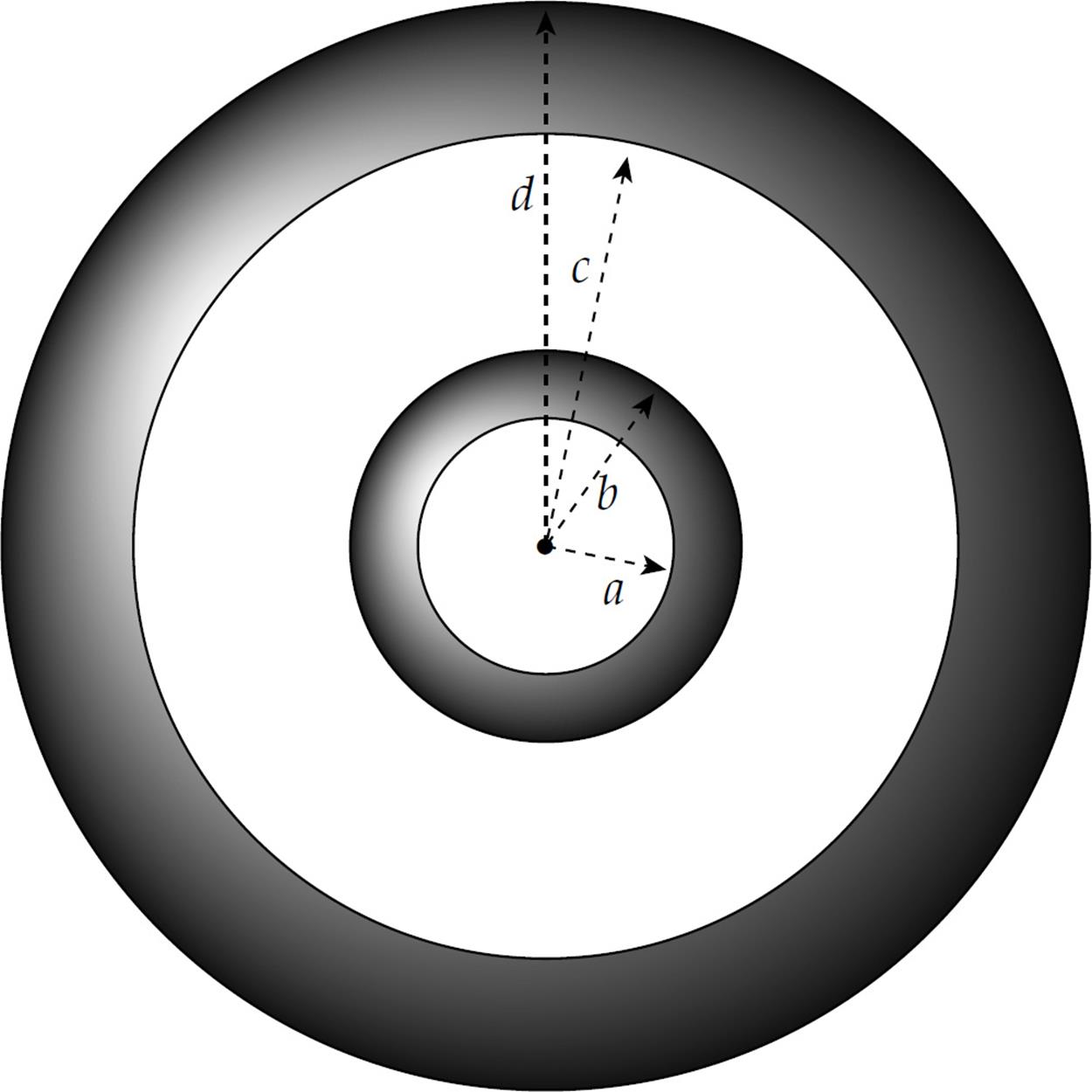
(a) Determine the electric field for

(i) r < a

(ii) a < r < b

(iii) b < r < c

(iv) c < r < d

(v) r > d

(b) Show in the figure the charges that reside on or inside each of the two shells.

4. A positively charged, thin nonconducting rod of length ℓ lies along the y axis with its midpoint at the origin. The linear charge density within the rod is uniform and denoted by λ. Points P₁ and P₂ lie on the positive x axis, at distances x₁ and x₂, respectively from the rod.

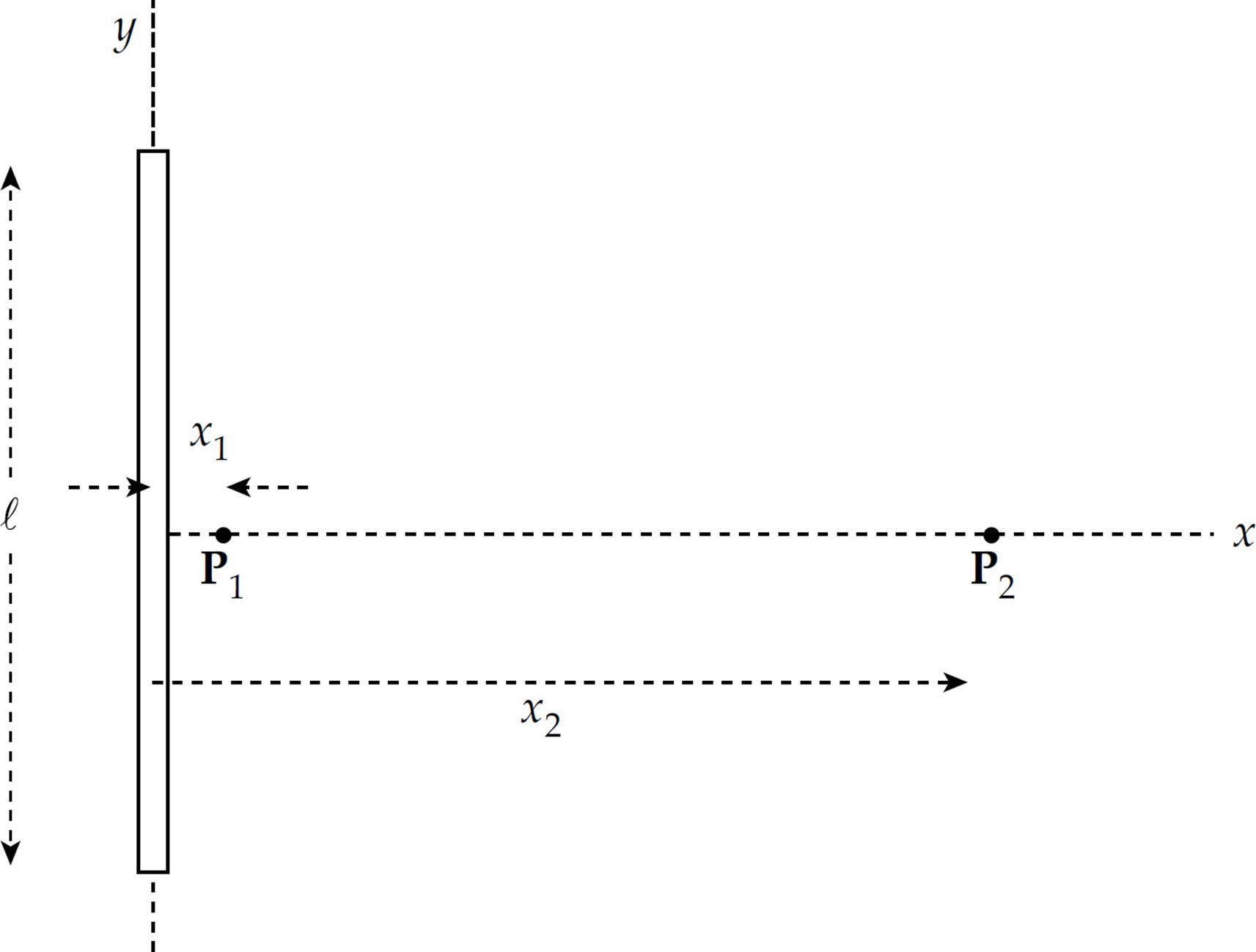
(a) Use Gauss’s Law to approximate the electric field at Point P₁, given that x₁ is very small compared to ℓ. Write your answer in terms of λ, x₁, and fundamental constants.

(b) What is the total charge Q on the rod?

(c) Compute the electric field at Point P₂, given that x₂ is not small compared to ℓ. For x₂ = ℓ, write your answer in terms of Q, ℓ, and fundamental constants. You may use the fact that

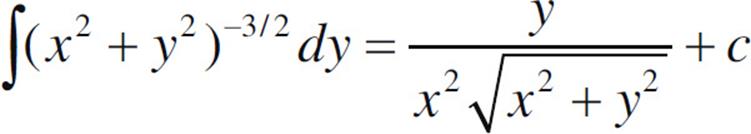
5. A solid glass sphere of radius a contains excess charge distributed throughout its volume such that the volume charge density depends on the distance r from the sphere’s center according to the equation

ρ(r) = ρ_s(r/a)

where ρ_s is a constant.

(a) What are the units of ρ_s?

(b) Compute the total charge Q on the sphere.

(i) r < a

(ii) r a

Write your answers to both (i) and (ii) in terms of Q, a, r, and fundamental constants.

(d) Sketch the electric field magnitude E as a function of r on the graph below. Be sure to indicate on the vertical axis the value of E at r = a.

Summary

General Information

There are positive and negative electric charges. Opposite charges attract and like charges repel.
Conductors allow charge to flow and insulators do not allow charge to flow.

Electric Forces

The force between two charges is given by Coulomb’s Law:

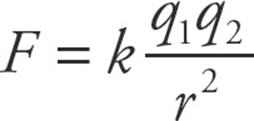
Electric Fields

The electric field indicates the direction of the force on a positive test charge, q.
The strength of the electric field is given by
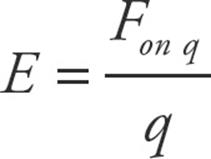
For a point charge, Q, the electric field is
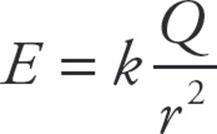
For distributed charge (see example 10):

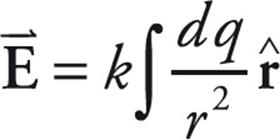
Electric Flux and Gauss’s Law

Electric flux is given by the number of electric field lines that pass through a surface.
It is given by the dot product of the electric field and area vector: Φ_E = E • A
For a variable electric field the flux is given by
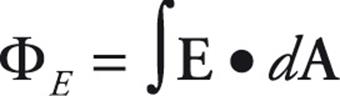
Gauss’s Law is given by the equation
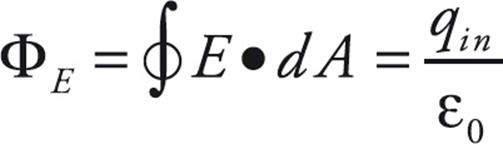
Gauss’s Law is generally used to solve for the electric field created by symmetric charge distributions (for example, spheres, spherical shells, lines of charge, and a sheet of charge).