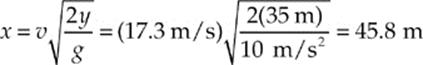AP Physics B Exam
20 AP Physics B Practice Exam 1: Answers and Explanations
SECTION I
1. D If the acceleration is not zero, then the velocity is changing. Since linear momentum (Item II) is the product of mass and velocity, it cannot remain constant if the velocity is changing. However, the object”s speed (Item I) could be constant (consider, for example, uniform circular motion), so its kinetic energy (Item III), the scalar K = ![]() mv2, could be constant as well.
mv2, could be constant as well.
2. E The gravitational force between the objects is given by
![]()
where m1 and m2 are the masses of the objects and r is the distance between their centers. If both masses are doubled and r is doubled, then the gravitational force will be
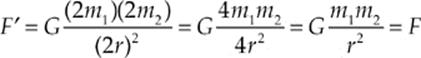
That is, the force remains the same.
3. D Since the particle travels in a circular path with constant kinetic energy (which implies constant speed), the net force on the particle is the centripetal force:
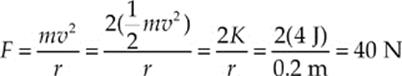
4. E Energy is a scalar, not a vector, quantity. Displacement, velocity, acceleration, and linear momentum (the product of mass and velocity) are all vector quantities.
5. D The acceleration of the block is a = g sin θ, where θ is the incline angle, and the distance it must travel—the length of the incline—is h/sin θ = h/sin 30° = 2h. Using the equation s = ![]() at2, we find that
at2, we find that
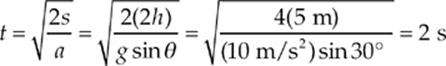
6. B The easiest way to answer this question is to use Conservation of Energy:
![]()
7. A Since the normal force is perpendicular to the object”s displacement, it does no work.
8. B The gravitational force provides the centripetal force on each satellite, so
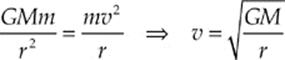
Therefore,
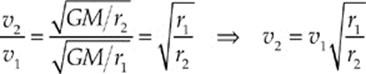
9. C The capacitance of a parallel-plate capacitor is C = κε0A/d where κ is the dielectric constant, A is the area of each plate, and d is their separation distance. Decreasing d will cause C to increase.
10. A The period is the reciprocal of the frequency: T = 1/f = 1/(2.5 Hz) = 0.4 s.
11. B One way to answer this question is to invent some numbers that satisfy the conditions of the question and observe what happens. Let”s choose f = 1 m, and take so1 = 3 m and so2 = 2 m (notice that f < so2 < so1, which means that the object is moving closer to the focal point). Using the mirror equation, we find that
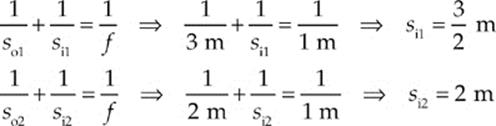
Since si2 > si1, the image is moving away from the mirror (eliminating choices (C) and (D)). Now for the magnifications:

Since |M2| > |M1|, the image gets taller. (You can also use ray diagrams.)
12. B The energies emitted during electron transitions are equal to the differences between the allowed energy levels. Choice (A), 17 eV, is equal to the energy emitted when the electron drops from the –21 eV level to the –38 eV level. Choice (C), 64 eV, is equal to the energy emitted when the electron drops from the –21 eV level to the –85 eV level. Choice (D), 255 eV, is equal to the energy emitted when the electron drops from the –85 eV level to the –340 eV level. And choice (E), 302 eV, is equal to the energy emitted when the electron drops from the –38 eV level to the –340 eV level. However, no electron transition in this atom could give rise to a 42 eV photon.
13. A Because the expansion is isothermal, no change in temperature occurs, which implies that no change in the internal energy of the gas takes place. Since ΔU = Q + W (the first law of thermodynamics), the fact that ΔU = 0 implies that Q = –W. Since W = –150 J, it must be true that Q = +150 J.
14. C The frequency does not change, so the wavelength must (because the wave speed changes):
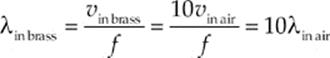
15. C The net force on the two-block system is 3mg – Ff, where Ff is the magnitude of the frictional force acting on the small block. Since Ff = μmg, we find that
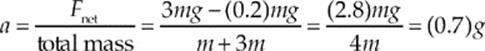
16. D By Newton”s Third Law, the force on the heavier person is equal but opposite to the force on the lighter person, eliminating choices (A) and (B). Since the lighter person has ![]() the mass of the heavier person and acceleration is inversely proportional to mass, the magnitude of the lighter person”s acceleration will be twice that of the heavier person.
the mass of the heavier person and acceleration is inversely proportional to mass, the magnitude of the lighter person”s acceleration will be twice that of the heavier person.
17. E The mass of the object is m = w/g = (6 N)/(10![]() ) = 0.6 kg, so the density of the object is ρ = m/V = (0.6 kg)/(2 × 10–3 m3) = 300 kg/m3. Since this is 30% of the density of water (ρwater = 1000 kg/m3), Archimedes” Principle tells us that 30% of the floating object”s volume will be submerged. This leaves 70% above the surface of the water.
) = 0.6 kg, so the density of the object is ρ = m/V = (0.6 kg)/(2 × 10–3 m3) = 300 kg/m3. Since this is 30% of the density of water (ρwater = 1000 kg/m3), Archimedes” Principle tells us that 30% of the floating object”s volume will be submerged. This leaves 70% above the surface of the water.
18. A If the mass of the +q charge is m, then its acceleration is
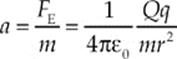
The graph in (A) best depicts an inverse-square relationship between a and r.
19. D When the block comes to rest, the spring force, kx, balances the gravitational force, mg. Therefore,
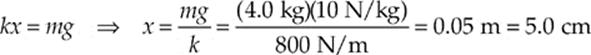
20. E Since the crate is being lifted with constant velocity, the magnitude of the force exerted by the crane must also be constant and equal to the magnitude of the gravitational force on the crate. Power can then be found from the equation
P = Fv = (5000 N)(4 m/s) = 20,000 W
21. C When the particle enters the magnetic field, the magnetic force provides the centripetal force to cause the particle to execute uniform circular motion:
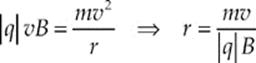
Since v and B are the same for all the particles, the largest r is found by maximizing the ratio m/|q|. The value of m/|q| for an alpha particle is about twice that for a proton and thousands of times greater than that of an electron or positron.
22. B The value of g near the surface of a planet depends on the planet”s mass and radius:
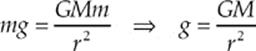
Therefore, calling this Planet X, we find that
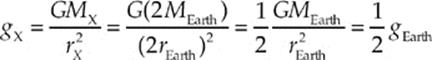
Since g is half as much on the planet as it is on Earth, the astronaut”s weight (mg) will be half as much as well.
23. E The maximum net force on the object occurs when all four forces act in the same direction, giving Fnet = 4F = 4(10 N) = 40 N, and a resulting acceleration of a = Fnet/m = (40 N)/(5 kg) = 8 m/s2. These four forces could not give the object an acceleration greater than this.
24. A The Carnot efficiency is equal to (TH – TC)/TH, where the temperatures are expressed in kelvins. Since 127°C = 127 + 273 = 400 K and 27°C = 27 + 273 = 300 K, we get
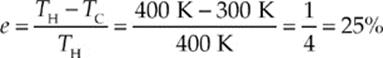
25. C The nth harmonic frequency is equal to n times the fundamental frequency, f1. Therefore,
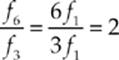
26. B We use the equation for the power dissipated by a resistor, P = IV:
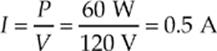
27. B A point charge placed at point A, B, or C would experience no net force only if the electric field at that point were zero. Let”s label the four charges 1, 2, 3, and 4, starting at the upper right and counting counterclockwise. The diagram below shows the individual electric field vectors at points A, B, and C due to the four charges.
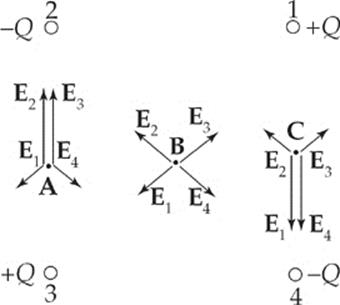
Only at point B do the four electric field vectors cancel each other to give a sum of zero, so only at point B would a charge feel no net force.
28. E The electric potential is a scalar, given by the formula V = kQ/r, where k = 1/4πε0 is Coulomb”s constant and r is the distance from the charge Q. In this case, the total potential at any point is the sum of the four potentials produced by the four source charges. Here”s the computation of the potential at each of the points A, B, and C, where a denotes the length of each side of the square in the diagram. Note that all of them equal zero.
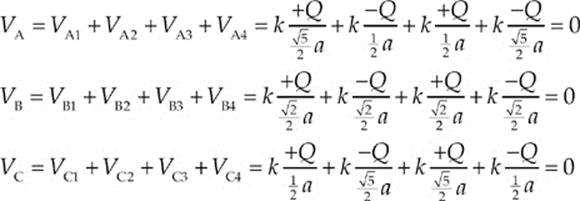
29. D The buoyant force is given by FB = ρairVsubg. Because the entire balloon is surrounded by air, Vsub is equal to V, the full volume of the balloon. Therefore, the buoyant force is proportional to the balloon”s volume. Since the volume of a sphere is given by V = ![]() πr3, if r is doubled, V will increase by a factor of 23 = 8. Thus, FB increases by a factor of 8.
πr3, if r is doubled, V will increase by a factor of 23 = 8. Thus, FB increases by a factor of 8.
30. C When a wave enters a new medium, its frequency does not change, but its wave speed does. Since λf = v, the change in wave speed implies a change in wavelength also.
31. D Since the magnetic flux out of the page is decreasing, the induced current will oppose this change (as always), attempting to create more magnetic flux out of the page. In order to do this, the current must circulate in the counterclockwise direction (remember the right-hand rule). As B decreases uniformly (that is, while ∆B/∆t is negative and constant), the induced emf,
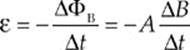
is nonzero and constant, which implies that the induced current, I = ε/R, is also nonzero and constant.
32. A The de Broglie wavelength of a particle moving with linear momentum of magnitude p = mv is given by the equation λ = h/p, where h is Planck”s constant. Because
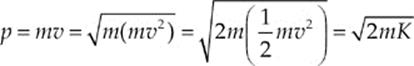
we find that
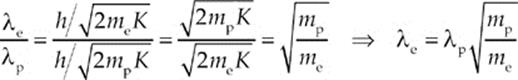
33. D With respect to the point at which the rod is attached to the vertical wall, the tension in the string exerts a counterclockwise (CCW) torque, and the gravitational force—which acts at the rod”s center of mass—exerts a clockwise (CW) torque. If the rod is in equilibrium, these torques must balance. Letting L denote the length of the rod, this gives
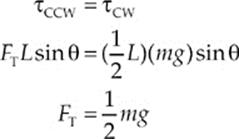
34. A Statement (B) is false, because a solid must absorb thermal energy in order to melt. Statement (C) is false since it generally requires much more energy to break the intermolecular bonds of a liquid to change its state to vapor than to loosen the intermolecular bonds of a solid to change its state to liquid. And statements (D) and (E) are false: While a substance undergoes a phase change, its temperature remains constant. The only true statement is (A).
35. C Relative to the central maximum, the locations of the bright fringes on the screen are given by the expression m(λL/d), where λ is the wavelength of the light used, L is the distance to the screen, d is the separation of the slits, and m is an integer. The width of a fringe is therefore (m + 1)(λL/d) – m(λL/d) = λL/d. One way to increase λL/d is to decrease d.
36. B Nuclear reactions must conserve mass number and charge, so the missing particle must be a proton:
![]()
37. D Resistors b, c, and d are equivalent to a single 1 Ω resistor, since
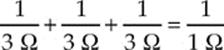
Therefore, the total resistance in the circuit is (3 Ω) + (1 Ω) + (3 Ω) + (3 Ω) = 10 Ω. From V = IR, we find that V = (3 A)(10 Ω) = 30 V.
38. E The power dissipated by a resistor is I2R. Since the current through Resistor b is ![]() of the current through Resistor e, we find that
of the current through Resistor e, we find that
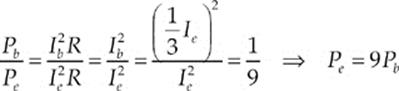
39. C If both the source and detector travel in the same direction and at the same speed, there will be no relative motion and hence no Doppler shift.
40. D The SI unit for power, P, is the watt, where 1 watt = 1 joule per second. One joule is equal to 1 newton·meter, and 1 newton = 1 kg·m/s2. Therefore,
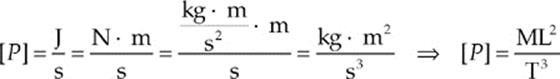
41. A In order for total internal reflection to occur, the beam must be incident in the medium with the higher index of refraction and strike the interface at an angle of incidence greater than the critical angle. Since v1 < v2, the refractive index of Medium 1, n1 = c/v1, must be greater than the index of Medium 2 (n2 = c/v2), and the critical angle is θc = sin–1(n2/n1) = sin–1(v1/v2).
42. A Because the initial height of the object is comparable to the radius of the Moon, we cannot simply use mgh for its initial potential energy. Instead, we must use the more general expression U = –GMm/r, where r is the distance from the center of the Moon. Note that since h = R, the object”s initial distance from the Moon”s center is h + R = R + R= 2R. Conservation of Energy then gives
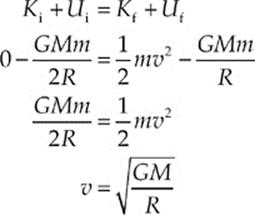
43. C Since the magnetic force is always perpendicular to the object”s velocity, it does zero work on any charged particle. Zero work means zero change in kinetic energy, so the speed remains the same. Remember: The magnetic force can only change the direction of a charged particle”s velocity, not its speed.
44. E The intensity of a wave is equal to the power delivered per unit area. By increasing the distance from the source by a factor of 2, the area is increased by a factor of 22 = 4. Since the intensity decreases by a factor that is less than 10, the sound level (in decibels) drops by an amount that is less than 10. The answer must be E.
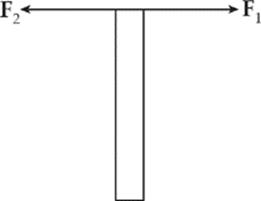
45. E By definition, an electric dipole consists of a pair of charges that are equal in magnitude but opposite in sign. The electric field at the point midway between the charges is equal to the sum of the electric fields due to each charge alone:
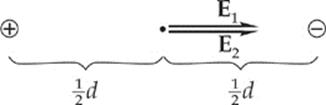
Because the individual electric field vectors point in the same direction, their magnitudes add to give the total electric field:
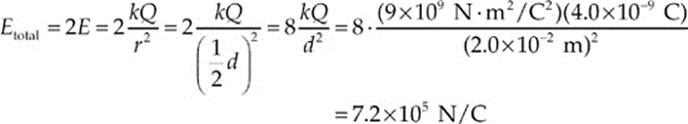
46. C By Newton”s Third Law, both vehicles experience the same magnitude of force and, therefore, the same impulse; so Statement I is false. Invoking Newton”s Second Law, in the form impulse = change in momentum, we see that Statement II is therefore also false. However, since the car has a smaller mass than the truck, its acceleration will be greater in magnitude than that of the truck, so Statement III is true.
47. B The projectile reaches its maximum height when its vertical velocity drops to zero. Since vy = v0y – gt, this occurs at time t = v0y/g after launch. The vertical displacement at this time is
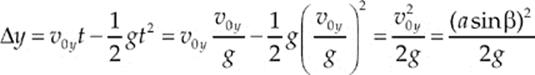
48. A At the instant a simple harmonic oscillator passes through equilibrium, the restoring force is zero. Therefore, the tangential acceleration of the pendulum bob is also zero.
49. D The angular momentum, L, of a particle is equal to rmv, so we must first determine v. Since the earth”s gravitational pull provides the centripetal force on the Moon,
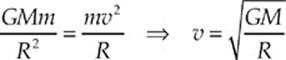
Therefore,
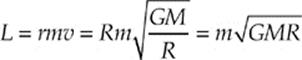
50. E If the photons of the incident light have insufficient energy to liberate electrons from the metal”s surface, then simply increasing the number of these weak photons (that is, increasing the intensity of the light) will do nothing. In order to produce photoelectrons, each photon of the incident light must have an energy at least as great as the work function of the metal.
51. D The force per unit length on each wire is (μ0/2π)I1I2/r, where r is the separation distance. Since I1 = I2 = I and r = a, the force per unit length on each wire is (μ0/2π)I2/a. Remember that when the currents are in opposite directions, the force between the wires is repulsive.
52. D The distance from the mirror to the image is equal to the distance from the mirror to the object. Therefore, the distance from the object to the image is 100 cm + 100 cm = 200 cm.
53. B Use the Ideal Gas Law:
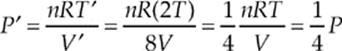
54. E The nuclide ![]() has 30 protons and 68 – 30 = 38 neutrons, so the excess number of neutrons over protons is 38 – 30 = 8. Of the choices given, only the nuclide
has 30 protons and 68 – 30 = 38 neutrons, so the excess number of neutrons over protons is 38 – 30 = 8. Of the choices given, only the nuclide ![]() shares this property; it has 35 protons and 78 – 35 = 43 neutrons, giving an excess of neutrons over protons of 43 – 35 = 8.
shares this property; it has 35 protons and 78 – 35 = 43 neutrons, giving an excess of neutrons over protons of 43 – 35 = 8.
55. B The charge on each plate has magnitude Q = CV = (2 × 10–3 F)(5 V) = 0.01 C.
56. C Use the work-energy theorem:
![]()
57. E Since the process is cyclic, ∆U = 0, neither choice (A) nor (B) can be true. Since the work done during an isochoric step is always zero (because there is no change in volume), choice (C) is incorrect also. Choice (D) is not true; for the cycle described—whether it”s clockwise or counterclockwise in a P–V diagram, the total work W will be negative. But choice (E) must be true; since ∆U= 0, the First Law of Thermodynamics says that W = –Q.
58. C Draw a free-body diagram:
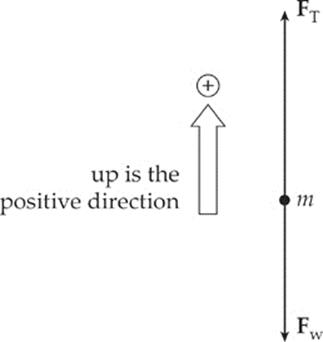
The net force on the object is F – FW, so
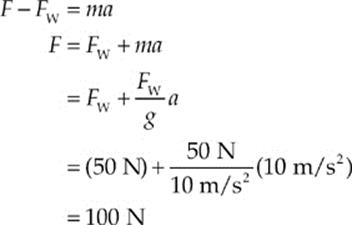
59. D The impulse delivered to the ball is equal to the ball”s change in momentum, and the presence of the mitt does not change this; choices (A) and (C) are eliminated. The extra area decreases the pressure on the catcher”s hand, but not the force, eliminating choice (B). The padding of the mitt causes the time during which the ball comes to a stop to increase, which decreases the magnitude of the ball”s acceleration (since a = ∆v/∆t). A decrease in the magnitude of the acceleration means a decrease in the magnitude of the force (since a = F/m).
60. C The Continuity Equation, Av = constant, tells us that v, the flow speed, is inversely proportional to A, the cross-sectional area of the pipe. Since A is proportional to d2, where d is the diameter of the pipe, we can say that v is inversely proportional to d2. Now, if d increases by a factor of 3/2 (from 2 cm to 3 cm), then v decreases by a factor of (3/2)2 = 9/4. Thus, the flow speed at the point where the pipe is 3 cm in diameter is (4/9)(18 m/s) = 8 m/s.
61. A A bi-convex lens is a converging lens, so it has a positive focal length. Since f = R/2, we have f = (20 cm)/2 = 10 cm. The lens equation then gives
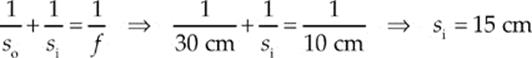
Because si is positive, the image is real, and real images are inverted. This eliminates choices (B), (C), and (D). The magnification is
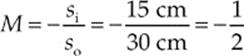
so the height of the image is
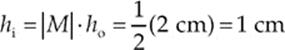
62. E If Lenz”s Law were violated, then energy conservation would also be violated. The other principles listed as choices are unrelated to Lenz”s law.
63. D Because no electrostatic field can exist within the body of a conductor, a charge of –1 mC will appear on the wall of the cavity to “guard” the +1 mC charge of the plastic ball. Since the sphere has a charge of +1 mC, a net charge of (+1 mC) – (–1 mC) = +2 mC will appear on the outer surface of the copper sphere.
64. A The resistance of a wire is given by the formula R = ρL/A, where ρ is the resistivity of the wire, L is its length, and A is its cross-sectional area. Since both wires are made of the same material, the value of ρ is the same for both wires, so we only need to look at the ratio L/A. Because the diameter of Wire Y is twice the diameter of Wire X, the cross-sectional area of Wire Y is 4 times the cross-sectional area of Wire X. Since
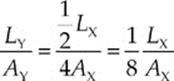
we see that the resistance of wire Y is 1/8 the resistance of wire X.
65. C The work required to charge the capacitor is equal to the resulting increase in the stored electrical potential energy:
![]()
66. A According to the Bernoulli effect, the flow speed will be lowest, and thus the pressure will be greatest, in the section of the pipe with the greatest diameter.
67. A Choices B, C, D, and E all change the magnetic flux through the loop containing the light bulb, thus inducing an emf and a current. However, just swinging the handle over as described in choice A changes neither the area presented to the magnetic field lines from the bottom coil nor the density of the field lines at the position of the loop. No change in magnetic flux means no induced emf and no induced current.
68. E Gamma rays and X-rays are very high-energy, short-wavelength radiations. Ultraviolet light has a higher energy and shorter wavelength than the visible spectrum. Within the visible spectrum, the colors are—in order of increasing frequency—ROYGBV, so orange light has a lower frequency (and thus longer wavelength) than blue light.
69. A If these waves interfere completely destructively, the displacement of the resultant wave will be 6 cm – 4 cm = 2 cm. If they interfere completely constructively, then the displacement of the resultant wave will be 6 cm + 4 cm = 10 cm. In general, then, the displacement of the resultant wave will be no less than 2 cm and no greater than 10 cm.
70. C Since Fnet = F1 + F2 = 0, the bar cannot accelerate translationally, so (B) is false. The net torque does not need to be zero, as the following diagram shows (eliminating choices (A) and (D)):
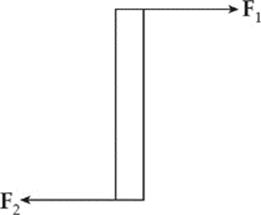
However, since F2 = –F1, choice (C) is true; one possible illustration of this is given below:
SECTION II
1. (a) The elastic potential energy of the spring turns into kinetic energy of the ball, which then becomes gravitational potential energy of the ball. Let the zero for gravitational potential energy be the initial position of the ball on the compressed spring (i.e., 8 cm below ground level). Then
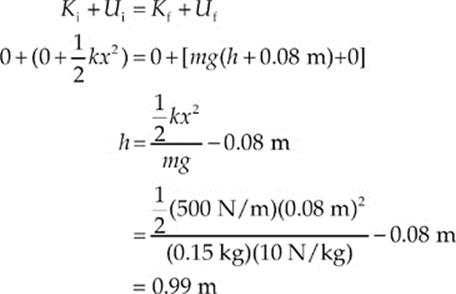
(b) (i) Use the impulse–momentum theorem (Newton”s Second Law):

(b) (ii) The ball is in flight until its vertical displacement is –h (calling up the positive direction). Therefore,
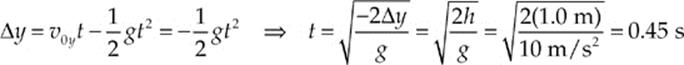
(b) (iii) The ball”s horizontal displacement is v0xt, where t is the time calculated in part
(b) (ii):
∆x = v0xt = (30 m/s)(0.45 s) = 13.5 m
(c) The frequency of this simple harmonic oscillator is
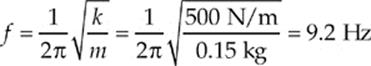
2. (a) Since the total resistance in the circuit is r + R, Ohm”s law gives
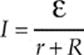
(b) The power dissipated as heat by resistor R is P = I2R; multiplying this by the time, t, gives Q, the heat dissipated:
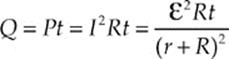
(c) (i) Use the equation Q = mc∆T with Q as given in part (b):
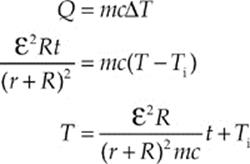
(c) (ii) The graph of T vs. t is a straight line with slope ε2R/[(r + R)2mc]:
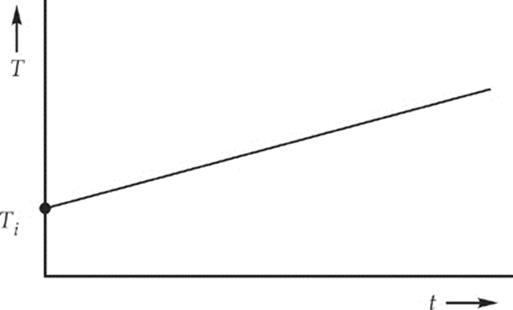
(d) The movement of the blades of the stirrer through the water transfers mechanical work to thermal energy. The faster the stirrer rotates (i.e., the more rotational kinetic energy it has), the more heat will be transferred to the water and the faster the temperature will rise. [In fact, given enough time, the rotating stirrer could bring the water to boil all by itself (assuming that heat losses to the beaker, the lid, etc. could be kept low)].
3. (a) Magnetic forces alone can only change the direction of a charged particle”s velocity, not its speed. This is because FB = q(v × B) is always perpendicular to v, the particle”s velocity, so it can do no work and thus cause no change in kinetic energy. The electric field is required to increase the particle”s speed.
(b) At the moment shown below, v is upward in the plane of the page, and F must point toward the center of the circular path.
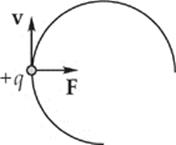
In order for FB = q(v × B) to be consistent with this, the right-hand rule implies that B must point out of the plane of the page (because q is positive).
(c) The time to complete one revolution, T, is equal to 2πr/v, where r is the radius of the path and v is the speed. Since the magnetic force provides the centripetal force,
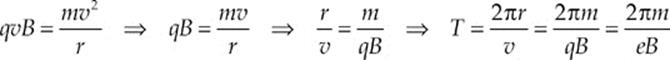
Therefore, T depends only on e, m, and B.
(d) Since T is the time for one revolution, the number of revolutions per unit time is the reciprocal of T, eB/(2πm).
(e) The description given with the problem states that “the voltage must be alternated twice during each revolution of the particle.” Therefore, the frequency of the alternating voltage must be twice the value found in part (d), 2eB/(2πm) = eB/(πm).
(f) From part (c), we know that
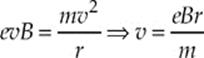
Therefore,
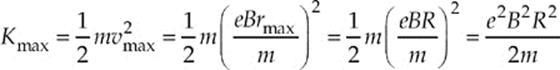
4. (a) First draw free-body diagrams for the blocks:
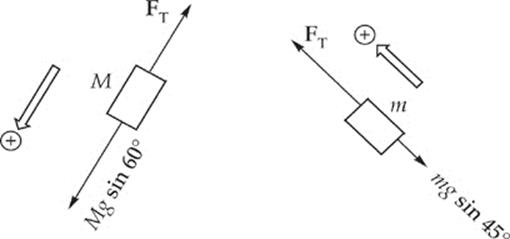
Now, apply Newton”s Second Law:
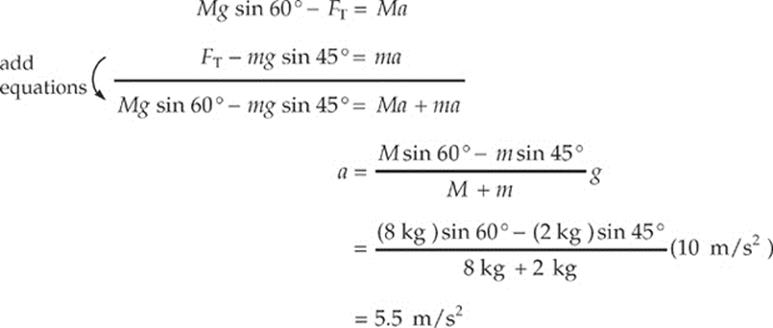
(b) Using the value for a determined above, find FT; we can use either of the two original equations from part (a):
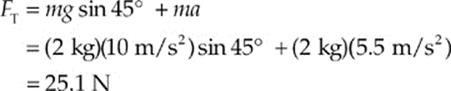
From the following diagram,
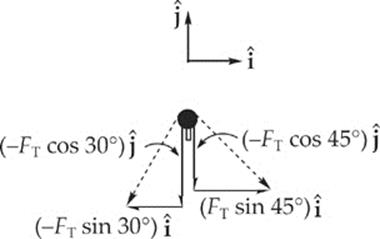
we see that the total force exerted by the cord on the peg is
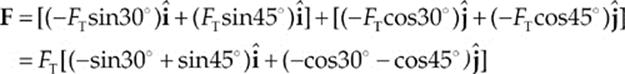
so

(c) Refer to the following diagram:
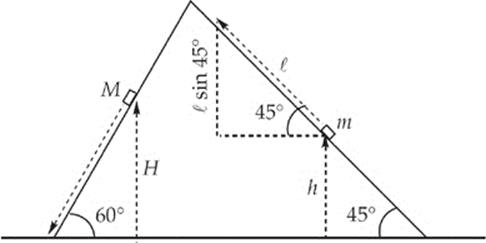
We have the constant acceleration of 5.5 m/s2 from part (a), so we may use v2 = v02 − 2a(x − x0). We know that v0 = 0 because it starts from rest. The distance M moves is given by: (x − x0) = 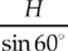 .
.
We now have:
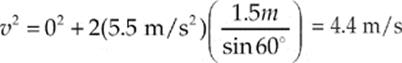
(d) First draw free-body diagrams for the blocks:
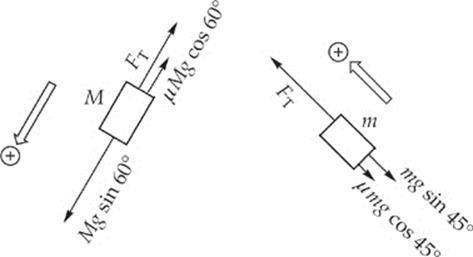
Now apply Newton”s Second Law:
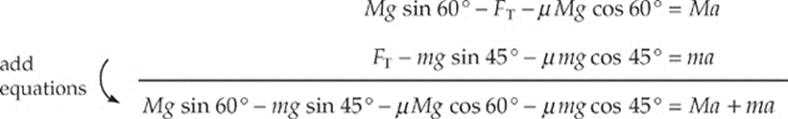
This gives

5. (a) The diagram given with the question shows that after the clay balls collide, they move in the –y direction, which means that the horizontal components of their linear momenta cancel. In other words, p1x + p2x = 0:
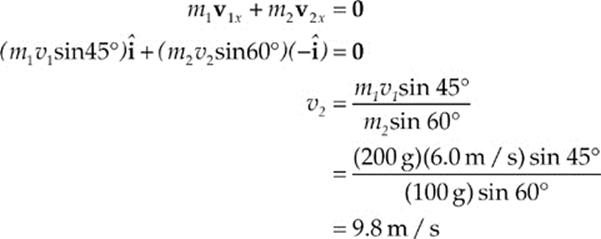
(b) Apply Conservation of Linear Momentum in the y direction:
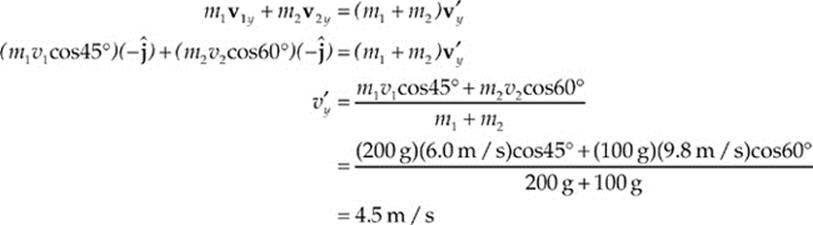
6. (a) We”ll consider two points in the flow stream: Point 1 at the surface of the water in the tank and Point 2 at the position of the hole. Because the cross-sectional area of the tank is so large, we can apply Torricelli”s theorem,
![]()
where y1 is the vertical distance from the ground to Point 1 and y2 is the vertical distance from the ground to Point 2. We conclude that the efflux speed of the water is
![]()
(b) The flow rate is equal to the cross-sectional area times the flow speed: f = Av. Using the result of part (a), we first find that
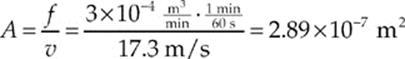
Since the area of the hole is given by A = πr2, we find that the radius of the hole is
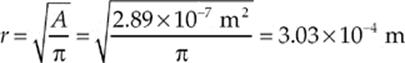
Therefore, the diameter of the hole is twice this value: d = 2r = 6.06 × 10−4 m.
(c) The horizontal distance, x, will be equal to vt, where v is the efflux speed we found in part (a) and t is the time it takes for water to reach the ground. Because the stream of water has zero vertical speed when it exits the hole, we can use the equation y = ![]() at2, with a = g, to find t. This gives
at2, with a = g, to find t. This gives
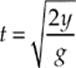
Since the vertical distance the water drops after exiting the hole is y = 35 m, the horizontal distance we”re looking for is