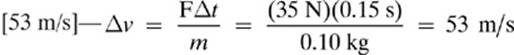Homework Helpers: Physics
3 Work, Energy, Power, and Momentum
Answer Key
The actual answers will be shown in brackets, followed by an explanation. If you don”t understand an explanation that is given in this section, you may want to go back and review the lesson that the question came from.
Lesson 3–1 Review
1. [work]—Remember: Only the force along the axis of the displacement is part of the work.
2. [138 J]—W = Fd cos θ = (20.0 N)(12.0 m)(cos 55.0°) = 138 J
3. 
4. [0 J]—The key here is that the weight is being held stationary. Without a displacement, no work is done.
5. [0 J]—The force exerted on the tray is in the upwards direction. The displacement of the tray is perpendicular to the force. Cosine 0° = 0, so no work is done.
Lesson 3–2 Review
1. [Kinetic energy]—If an object is not in motion, its velocity is zero, and so is the kinetic energy.
2. 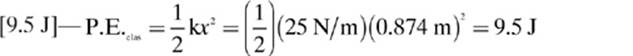
3. 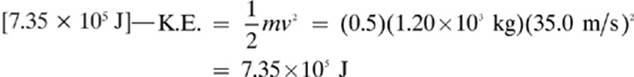
4. [180 J]—P.E.g = mgh = (6.0 kg)(9.81 m/s2)(3.0 m) = 176.58 J = 180 J with two significant digits
Lesson 3–3 Review
1. [353 J]—Because the ramp is frictionless, the law of conservation of mechanical energy tells us that the kinetic energy of the box at the bottom of the ramp will be equal to the gravitational potential energy that it had at the top of the ramp.
K.E. = P.E.grav = mgh = (12.0 kg)(9.81 m/s2)(3.00 m) = 353 J
2. [7.35 m/s]—We set the formulas for kinetic energy and gravitational potential energy equal to each other,
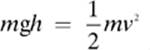
and then solve for velocity to get the working formula
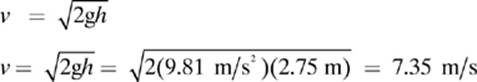
Notice that the mass of the apple plays no part in the equation. Despite what Aristotle thought, heavy objects do not fall faster than light ones.
3. [49.1 J]—At the top of the shelf, the bowling ball”s gravitational potential energy would be P.E.g = mgh = (5.00 kg)(9.81 m/s2)(2.00 m) = 98.1 J and the kinetic energy would be zero. When it has fallen 1.00 m, halfway to the floor, half of its gravitational potential energy will have turned into kinetic energy (98.1 J/2) = 49.1 J.
Lesson 3–4 Review
1. 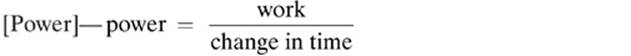
2. 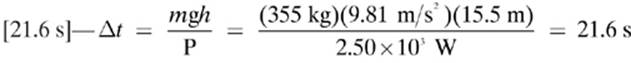
3. 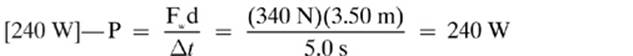
Lesson 3–5 Review
1. [elastic collision]—Think of elastic collision as the type of collision where the objects bounce apart. When they stick together, that is an inelastic collision.
2. [momentum]—p = mv
3. 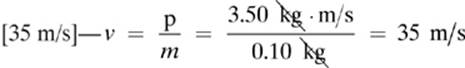
Lesson 3–6 Review
1. [Impulse]— J = FΔt
2. [3.00 × 102 N · s]— J = FΔt = (20.0 N)(15.0 s) = 3.00 × 102 N · s
3. 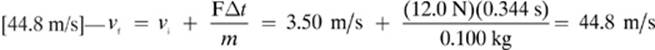
Chapter 3 Examination
1. ![]()
2. [f. mechanical energy]—Do you remember the law of conservation of mechanical energy?
3. [h. momentum]—Momentum is calculated with the formula p = mv.
4. [c. kinetic energy]—If an object”s velocity is zero, its kinetic energy is also zero.
5. [i. impulse]— J = FΔt
6. [b. watts]—Power is measured in watts (1 watt = 1 joule/second).
7. [d. quadrupled]—Remember: The kinetic energy of an object is proportional to the square of its velocity.
![]()
8. [a. 0.127 kg]—We know that P.E.g = mgh, so
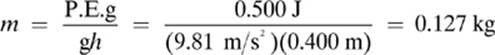
9. [b. 0.400 J]—When the apple has fallen half the distance, the value for height (h) in the equation P.E.g = mgh will be half the original value.
10. [d. 20.0 J]—Questions such as number 10 are designed to throw off people who simply take whatever numbers there are in the question and pick an operation to do at random. The only quantities we need to solve this one are the force and displacement. W = Fd = (5.00 N)(4.00 m) = 20.0 J
11. 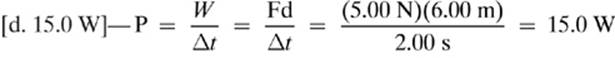
12. 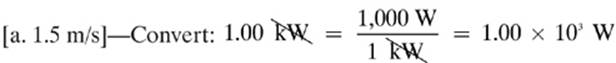
Remember: Another formula for power is P = fv, so
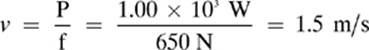
13. 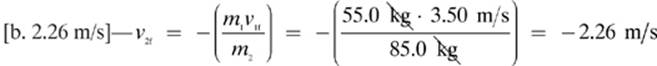
Because the question only asks for the speed, we will only report the magnitude of the velocity, 2.26 m/s.
14. 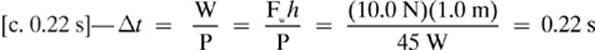
15. 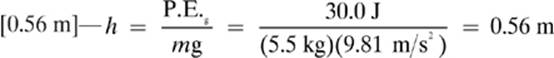
16. 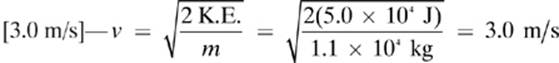
17. 
18. ![]()
19. [7.0 × 102 kg · m/s]—p = mv = (140 kg)(5.0 m/s) = 7.0 × 102 kg · m/s
20.